Smart Alex

Alex was aptly named because she’s, like, super smart. She likes teaching people, and her hobby is posing people questions so that she can explain the answers to them. Alex appears at the end of each chapter of Discovering Statistics Using IBM SPSS Statistics (6th edition) to pose you some questions and give you tasks to help you to practice your data analysis skills. This page contains her answers to those questions.
Chapter 1
Task 1.1
What are (broadly speaking) the five stages of the research process?
- Generating a research question: through an initial observation (hopefully backed up by some data).
- Generate a theory to explain your initial observation.
- Generate hypotheses: break your theory down into a set of testable predictions.
- Collect data to test the theory: decide on what variables you need to measure to test your predictions and how best to measure or manipulate those variables.
- Analyse the data: look at the data visually and by fitting a statistical model to see if it supports your predictions (and therefore your theory). At this point you should return to your theory and revise it if necessary.
Task 1.2
What is the fundamental difference between experimental and correlational research?
In a word, causality. In experimental research we manipulate a variable (predictor, independent variable) to see what effect it has on another variable (outcome, dependent variable). This manipulation, if done properly, allows us to compare situations where the causal factor is present to situations where it is absent. Therefore, if there are differences between these situations, we can attribute cause to the variable that we manipulated. In correlational research, we measure things that naturally occur and so we cannot attribute cause but instead look at natural covariation between variables.
Task 1.3
What is the level of measurement of the following variables?
- The number of downloads of different bands’ songs on iTunes:
- This is a discrete ratio measure. It is discrete because you can download only whole songs, and it is ratio because it has a true and meaningful zero (no downloads at all).
- The names of the bands downloaded.
- This is a nominal variable. Bands can be identified by their name, but the names have no meaningful order. The fact that Norwegian black metal band 1349 called themselves 1349 does not make them better than British boy-band has-beens 911; the fact that 911 were a bunch of talentless idiots does, though.
- Their positions in the download chart.
- This is an ordinal variable. We know that the band at number 1 sold more than the band at number 2 or 3 (and so on) but we don’t know how many more downloads they had. So, this variable tells us the order of magnitude of downloads, but doesn’t tell us how many downloads there actually were.
- The money earned by the bands from the downloads.
- This variable is continuous and ratio. It is continuous because money (pounds, dollars, euros or whatever) can be broken down into very small amounts (you can earn fractions of euros even though there may not be an actual coin to represent these fractions).
- The weight of drugs bought by the band with their royalties.
- This variable is continuous and ratio. If the drummer buys 100 g of cocaine and the singer buys 1 kg, then the singer has 10 times as much.
- The type of drugs bought by the band with their royalties.
- This variable is categorical and nominal: the name of the drug tells us something meaningful (crack, cannabis, amphetamine, etc.) but has no meaningful order.
- The phone numbers that the bands obtained because of their fame.
- This variable is categorical and nominal too: the phone numbers have no meaningful order; they might as well be letters. A bigger phone number did not mean that it was given by a better person.
- The gender of the people giving the bands their phone numbers.
- This variable is categorical: the people dishing out their phone numbers could fall into one of several categories based on how they self-identify when asked about their gender (their gender identity could be fluid). Taking a very simplistic view of gender, the variable might contain categories of male, female, and non-binary.
- This variable is categorical: the people dishing out their phone numbers could fall into one of several categories based on how they self-identify when asked about their gender (their gender identity could be fluid). Taking a very simplistic view of gender, the variable might contain categories of male, female, and non-binary.
- The instruments played by the band members.
- This variable is categorical and nominal too: the instruments have no meaningful order but their names tell us something useful (guitar, bass, drums, etc.).
- The time they had spent learning to play their instruments.
- This is a continuous and ratio variable. The amount of time could be split into infinitely small divisions (nanoseconds even) and there is a meaningful true zero (no time spent learning your instrument means that, like 911, you can’t play at all).
Task 1.4
Say I own 857 CDs. My friend has written a computer program that uses a webcam to scan my shelves in my house where I keep my CDs and measure how many I have. His program says that I have 863 CDs. Define measurement error. What is the measurement error in my friend’s CD counting device?
Measurement error is the difference between the true value of something and the numbers used to represent that value. In this trivial example, the measurement error is 6 CDs. In this example we know the true value of what we’re measuring; usually we don’t have this information, so we have to estimate this error rather than knowing its actual value.
Task 1.5
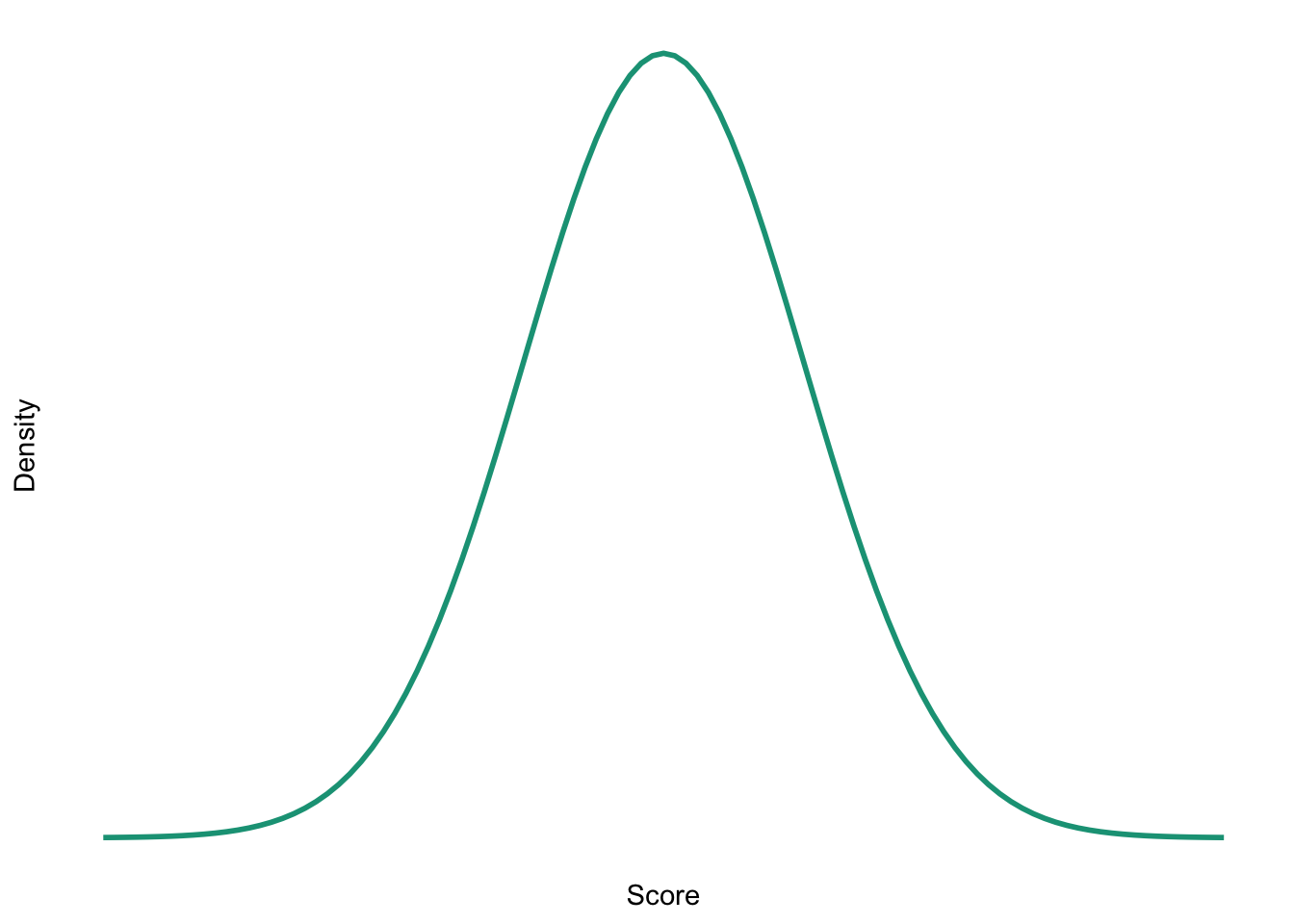
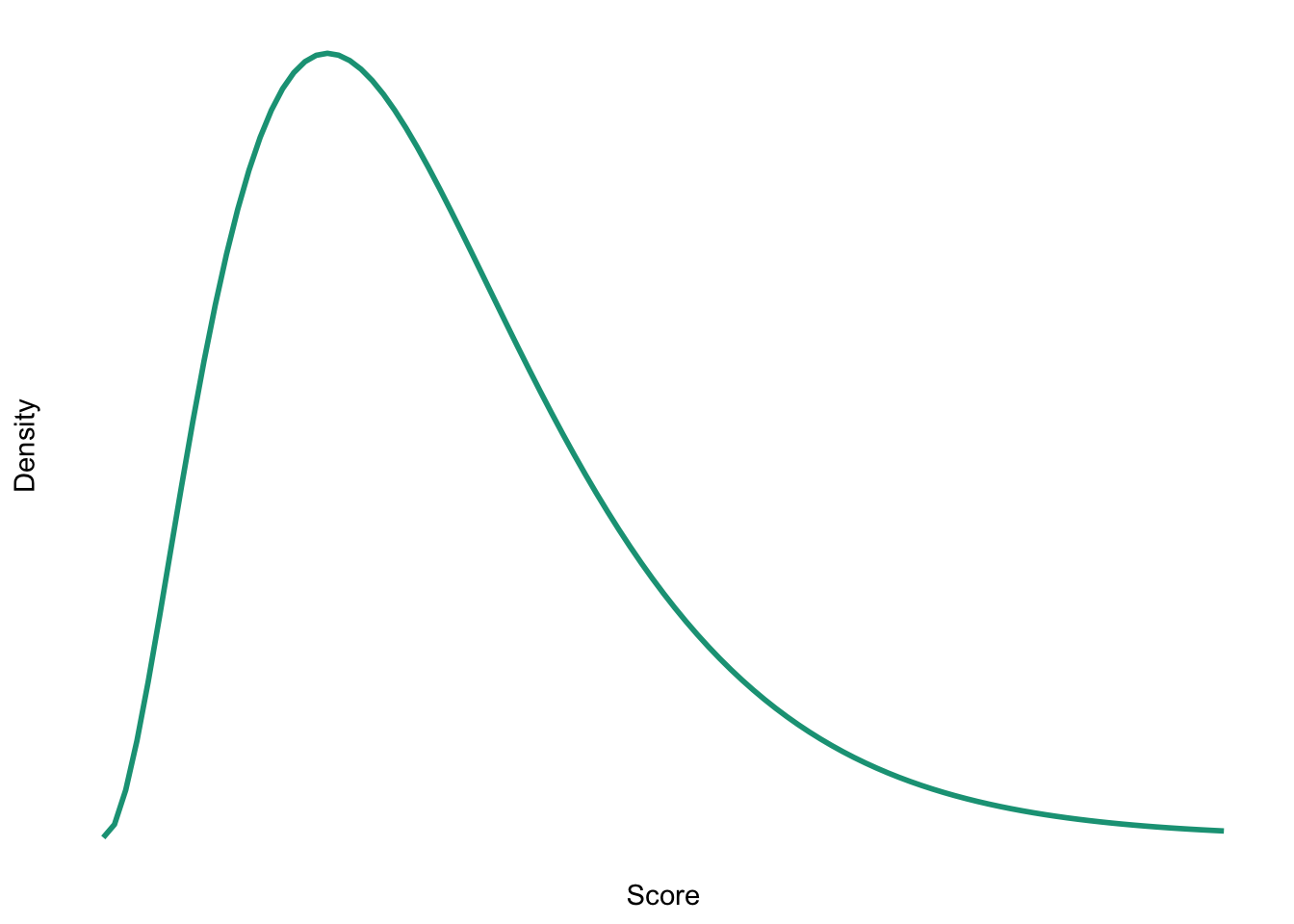
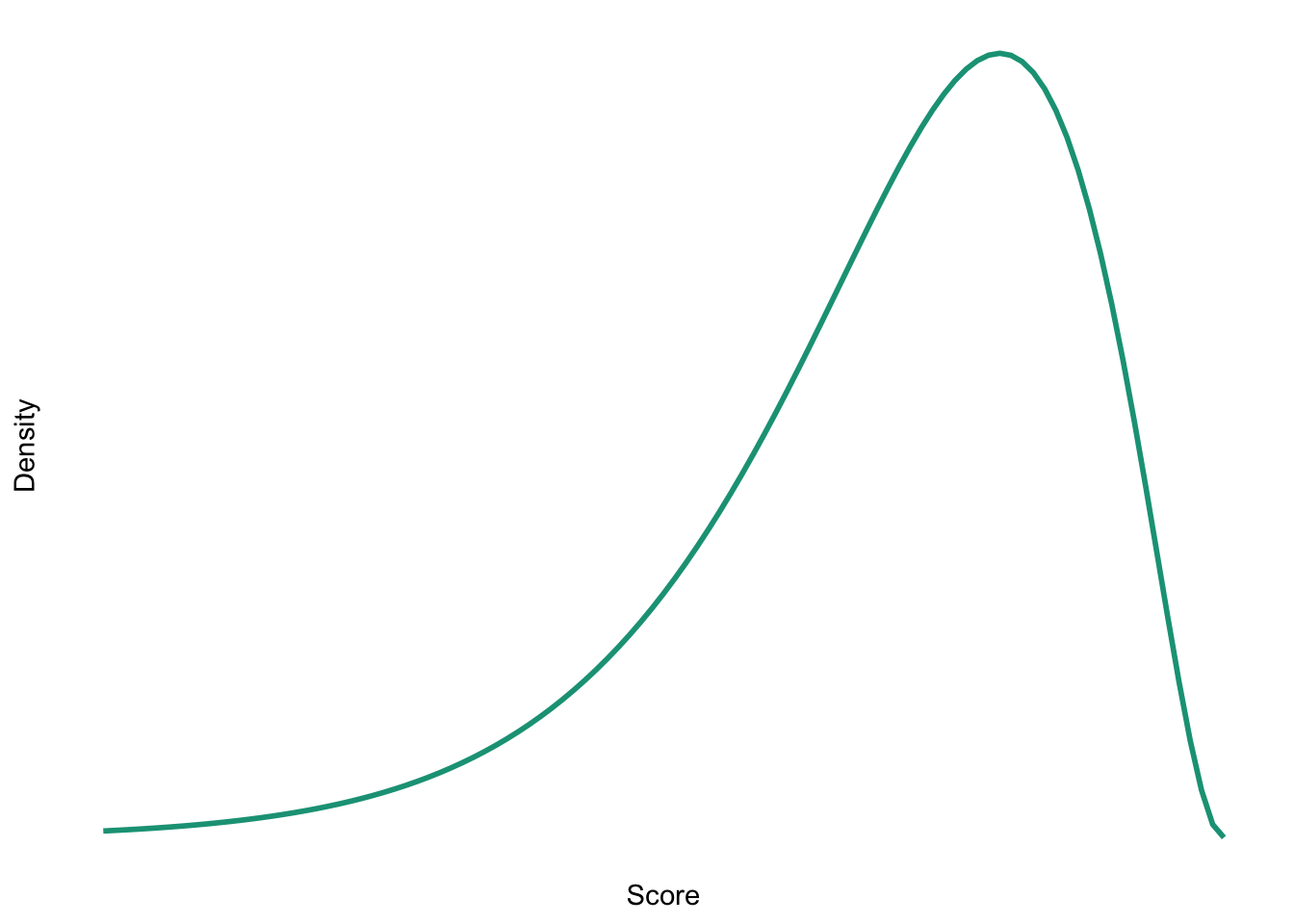
Sketch the shape of a normal distribution, a positively skewed distribution and a negatively skewed distribution.
Normal
Positive skew
Negative skew
Task 1.6
In 2011 I got married and we went to Disney Florida for our honeymoon. We bought some bride and groom Mickey Mouse hats and wore them around the parks. The staff at Disney are really nice and upon seeing our hats would say ‘congratulations’ to us. We counted how many times people said congratulations over 7 days of the honeymoon: 5, 13, 7, 14, 11, 9, 17. Calculate the mean, median, sum of squares, variance and standard deviation of these data.
First compute the mean:
\[ \begin{aligned} \overline{X} &= \frac{\sum_{i=1}^{n} x_i}{n} \\ &= \frac{5+13+7+14+11+9+17}{7} \\ &= \frac{76}{7} \\ &= 10.86 \end{aligned} \]
To calculate the median, first let’s arrange the scores in ascending order: 5, 7, 9, 11, 13, 14, 17. The median will be the (n + 1)/2th score. There are 7 scores, so this will be the 8/2 = 4th. The 4th score in our ordered list is 11.
To calculate the sum of squares, first take the mean from each score, then square this difference, finally, add up these squared values:
| Score | Error (score - mean) | Error squared | |
|---|---|---|---|
| 5 | -5.86 | 34.34 | |
| 13 | 2.14 | 4.58 | |
| 7 | -3.86 | 14.90 | |
| 14 | 3.14 | 9.86 | |
| 11 | 0.14 | 0.02 | |
| 9 | -1.86 | 3.46 | |
| 17 | 6.14 | 37.70 | |
| Total | — | — | 104.86 |
So, the sum of squared errors is:
\[ \begin{aligned} \text{SS} &= 34.34 + 4.58 + 14.90 + 9.86 + 0.02 + 3.46 + 37.70 \\ &= 104.86 \\ \end{aligned} \]
The variance is the sum of squared errors divided by the degrees of freedom:
\[ \begin{aligned} s^2 &= \frac{SS}{N - 1} \\ &= \frac{104.86}{6} \\ &= 17.48 \end{aligned} \]
The standard deviation is the square root of the variance:
\[ \begin{aligned} s &= \sqrt{s^2} \\ &= \sqrt{17.48} \\ &= 4.18 \end{aligned} \]
Task 1.7
In this chapter we used an example of the time taken for 21 heavy smokers to fall off a treadmill at the fastest setting (18, 16, 18, 24, 23, 22, 22, 23, 26, 29, 32, 34, 34, 36, 36, 43, 42, 49, 46, 46, 57). Calculate the sums of squares, variance and standard deviation of these data.
To calculate the sum of squares, take the mean from each value, then square this difference. Finally, add up these squared values (the values in the final column). The sum of squared errors is a massive 2685.24.
| Score | Mean | Difference | Difference squared | |
|---|---|---|---|---|
| 18 | 32.19 | -14.19 | 201.356 | |
| 16 | 32.19 | -16.19 | 262.116 | |
| 18 | 32.19 | -14.19 | 201.356 | |
| 24 | 32.19 | -8.19 | 67.076 | |
| 23 | 32.19 | -9.19 | 84.456 | |
| 22 | 32.19 | -10.19 | 103.836 | |
| 22 | 32.19 | -10.19 | 103.836 | |
| 23 | 32.19 | -9.19 | 84.456 | |
| 26 | 32.19 | -6.19 | 38.316 | |
| 29 | 32.19 | -3.19 | 10.176 | |
| 32 | 32.19 | -0.19 | 0.036 | |
| 34 | 32.19 | 1.81 | 3.276 | |
| 34 | 32.19 | 1.81 | 3.276 | |
| 36 | 32.19 | 3.81 | 14.516 | |
| 36 | 32.19 | 3.81 | 14.516 | |
| 43 | 32.19 | 10.81 | 116.856 | |
| 42 | 32.19 | 9.81 | 96.236 | |
| 49 | 32.19 | 16.81 | 282.576 | |
| 46 | 32.19 | 13.81 | 190.716 | |
| 46 | 32.19 | 13.81 | 190.716 | |
| 57 | 32.19 | 24.81 | 615.536 | |
| Total | — | — | — | 2685.236 |
The variance is the sum of squared errors divided by the degrees of freedom (\(N-1\)). There were 21 scores and so the degrees of freedom were 20. The variance is, therefore:
\[ \begin{aligned} s^2 &= \frac{SS}{N - 1} \\ &= \frac{2685.24}{20} \\ &= 134.26 \end{aligned} \]
The standard deviation is the square root of the variance:
\[ \begin{aligned} s &= \sqrt{s^2} \\ &= \sqrt{134.26} \\ &= 11.59 \end{aligned} \]
Task 1.8
Sports scientists sometimes talk of a ‘red zone’, which is a period during which players in a team are more likely to pick up injuries because they are fatigued. When a player hits the red zone it is a good idea to rest them for a game or two. At a prominent London football club that I support, they measured how many consecutive games the 11 first team players could manage before hitting the red zone: 10, 16, 8, 9, 6, 8, 9, 11, 12, 19, 5. Calculate the mean, standard deviation, median, range and interquartile range.
First we need to compute the mean:
\[ \begin{aligned} \overline{X} &= \frac{\sum_{i=1}^{n} x_i}{n} \\ &= \frac{10+16+8+9+6+8+9+11+12+19+5}{11} \\ &= \frac{113}{11} \\ &= 10.27 \end{aligned} \]
Then the standard deviation, which we do as follows:
| Score | Error (score - mean) | Error squared | |
|---|---|---|---|
| 10 | -0.27 | 0.07 | |
| 16 | 5.73 | 32.83 | |
| 8 | -2.27 | 5.15 | |
| 9 | -1.27 | 1.61 | |
| 6 | -4.27 | 18.23 | |
| 8 | -2.27 | 5.15 | |
| 9 | -1.27 | 1.61 | |
| 11 | 0.73 | 0.53 | |
| 12 | 1.73 | 2.99 | |
| 19 | 8.73 | 76.21 | |
| 5 | -5.27 | 27.77 | |
| Total | — | — | 172.15 |
So, the sum of squared errors is:
\[ \begin{aligned} \text{SS} &= 0.07 + 32.83 + 5.15 + 1.61 + 18.23 + 5.15 + 1.61 + 0.53 + 2.99 + 76.21 + 27.77 \\ &= 172.15 \\ \end{aligned} \]
The variance is the sum of squared errors divided by the degrees of freedom:
\[ \begin{aligned} s^2 &= \frac{SS}{N - 1} \\ &= \frac{172.15}{10} \\ &= 17.22 \end{aligned} \]
The standard deviation is the square root of the variance:
\[ \begin{aligned} s &= \sqrt{s^2} \\ &= \sqrt{17.22} \\ &= 4.15 \end{aligned} \]
- To calculate the median, range and interquartile range, first let’s arrange the scores in ascending order: 5, 6, 8, 8, 9, 9, 10, 11, 12, 16, 19. The median: The median will be the (\(n + 1\))/2th score. There are 11 scores, so this will be the 12/2 = 6th. The 6th score in our ordered list is 9 games. Therefore, the median number of games is 9.
- The lower quartile: This is the median of the lower half of scores. If we split the data at 9 (the 6th score), there are 5 scores below this value. The median of 5 = 6/2 = 3rd score. The 3rd score is 8, the lower quartile is therefore 8 games.
- The upper quartile: This is the median of the upper half of scores. If we split the data at 9 again (not including this score), there are 5 scores above this value. The median of 5 = 6/2 = 3rd score above the median. The 3rd score above the median is 12; the upper quartile is therefore 12 games.
- The range: This is the highest score (19) minus the lowest (5), i.e. 14 games.
- The interquartile range: This is the difference between the upper and lower quartile: 12−8 = 4 games.
Task 1.9
Celebrities always seem to be getting divorced. The (approximate) length of some celebrity marriages in days are: 240 (J-Lo and Cris Judd), 144 (Charlie Sheen and Donna Peele), 143 (Pamela Anderson and Kid Rock), 72 (Kim Kardashian, if you can call her a celebrity), 30 (Drew Barrymore and Jeremy Thomas), 26 (Axl Rose and Erin Everly), 2 (Britney Spears and Jason Alexander), 150 (Drew Barrymore again, but this time with Tom Green), 14 (Eddie Murphy and Tracy Edmonds), 150 (Renee Zellweger and Kenny Chesney), 1657 (Jennifer Aniston and Brad Pitt). Compute the mean, median, standard deviation, range and interquartile range for these lengths of celebrity marriages.
First we need to compute the mean:
\[ \begin{aligned} \overline{X} &= \frac{\sum_{i=1}^{n} x_i}{n} \\ &= \frac{240+144+143+72+30+26+2+150+14+150+1657}{11} \\ &= \frac{2628}{11} \\ &= 238.91 \end{aligned} \]
Then the standard deviation, which we do as follows:
| Score | Error (score - mean) | Error squared | |
|---|---|---|---|
| 240 | 1.09 | 1.19 | |
| 144 | -94.91 | 9007.91 | |
| 143 | -95.91 | 9198.73 | |
| 72 | -166.91 | 27858.95 | |
| 30 | -208.91 | 43643.39 | |
| 26 | -212.91 | 45330.67 | |
| 2 | -236.91 | 56126.35 | |
| 150 | -88.91 | 7904.99 | |
| 14 | -224.91 | 50584.51 | |
| 150 | -88.91 | 7904.99 | |
| 1657 | 1418.09 | 2010979.25 | |
| Total | — | — | 2268541 |
So, the sum of squared errors is the sum of the final column. The variance is the sum of squared errors divided by the degrees of freedom:
\[ \begin{aligned} s^2 &= \frac{SS}{N - 1} \\ &= \frac{2268541}{10} \\ &= 226854.1 \end{aligned} \]
The standard deviation is the square root of the variance:
\[ \begin{aligned} s &= \sqrt{s^2} \\ &= \sqrt{226854.1} \\ &= 476.29 \end{aligned} \]
- To calculate the median, range and interquartile range, first let’s arrange the scores in ascending order: 2, 14, 26, 30, 72, 143, 144, 150, 150, 240, 1657. The median: The median will be the (n + 1)/2th score. There are 11 scores, so this will be the 12/2 = 6th. The 6th score in our ordered list is 143. The median length of these celebrity marriages is therefore 143 days.
- The lower quartile: This is the median of the lower half of scores. If we split the data at 143 (the 6th score), there are 5 scores below this value. The median of 5 = 6/2 = 3rd score. The 3rd score is 26, the lower quartile is therefore 26 days.
- The upper quartile: This is the median of the upper half of scores. If we split the data at 143 again (not including this score), there are 5 scores above this value. The median of 5 = 6/2 = 3rd score above the median. The 3rd score above the median is 150; the upper quartile is therefore 150 days.
- The range: This is the highest score (1657) minus the lowest (2), i.e. 1655 days.
- The interquartile range: This is the difference between the upper and lower quartile: 150−26 = 124 days.
Task 1.10
Repeat Task 9 but excluding Jennifer Anniston and Brad Pitt’s marriage. How does this affect the mean, median, range, interquartile range, and standard deviation? What do the differences in values between Tasks 9 and 10 tell us about the influence of unusual scores on these measures?
First let’s compute the new mean:
\[ \begin{aligned} \overline{X} &= \frac{\sum_{i=1}^{n} x_i}{n} \\ &= \frac{240+144+143+72+30+26+2+150+14+150}{11} \\ &= \frac{971}{11} \\ &= 97.1 \end{aligned} \]
The mean length of celebrity marriages is now 97.1 days compared to 238.91 days when Jennifer Aniston and Brad Pitt’s marriage was included. This demonstrates that the mean is greatly influenced by extreme scores.
Let’s now calculate the standard deviation excluding Jennifer Aniston and Brad Pitt’s marriage:
| Score | Error (score - mean) | Error squared | |
|---|---|---|---|
| 240 | 142.9 | 20420.41 | |
| 144 | 46.9 | 2199.61 | |
| 143 | 45.9 | 2106.81 | |
| 72 | -25.1 | 630.01 | |
| 30 | -67.1 | 4502.41 | |
| 26 | -71.1 | 5055.21 | |
| 2 | -95.1 | 9044.01 | |
| 150 | 52.9 | 2798.41 | |
| 14 | -83.1 | 6905.61 | |
| 150 | 52.9 | 2798.41 | |
| Total | — | — | 56460.9 |
So, the sum of squared errors is:
\[ \begin{aligned} \text{SS} &= 20420.41 + 2199.61 + 2106.81 + 630.01 + 4502.41 + 5055.21 + 9044.01 + 2798.41 + 6905.61 + 2798.41 \\ &= 56460.90 \\ \end{aligned} \]
The variance is the sum of squared errors divided by the degrees of freedom:
\[ \begin{aligned} s^2 &= \frac{SS}{N - 1} \\ &= \frac{56460.90}{9} \\ &= 6273.43 \end{aligned} \]
The standard deviation is the square root of the variance:
\[ \begin{aligned} s &= \sqrt{s^2} \\ &= \sqrt{6273.43} \\ &= 79.21 \end{aligned} \]
From these calculations we can see that the variance and standard deviation, like the mean, are both greatly influenced by extreme scores. When Jennifer Aniston and Brad Pitt’s marriage was included in the calculations (see Smart Alex Task 9), the variance and standard deviation were much larger, i.e. 226854.09 and 476.29 respectively.
- To calculate the median, range and interquartile range, first, let’s again arrange the scores in ascending order but this time excluding Jennifer Aniston and Brad Pitt’s marriage: 2, 14, 26, 30, 72, 143, 144, 150, 150, 240.
- The median: The median will be the (n + 1)/2 score. There are now 10 scores, so this will be the 11/2 = 5.5th. Therefore, we take the average of the 5th score and the 6th score. The 5th score is 72, and the 6th is 143; the median is therefore 107.5 days.
- The lower quartile: This is the median of the lower half of scores. If we split the data at 107.5 (this score is not in the data set), there are 5 scores below this value. The median of 5 = 6/2 = 3rd score. The 3rd score is 26; the lower quartile is therefore 26 days.
- The upper quartile: This is the median of the upper half of scores. If we split the data at 107.5 (this score is not actually present in the data set), there are 5 scores above this value. The median of 5 = 6/2 = 3rd score above the median. The 3rd score above the median is 150; the upper quartile is therefore 150 days.
- The range: This is the highest score (240) minus the lowest (2), i.e. 238 days. You’ll notice that without the extreme score the range drops dramatically from 1655 to 238 – less than half the size.
- The interquartile range: This is the difference between the upper and lower quartile: 150 − 26 = 124 days of marriage. This is the same as the value we got when Jennifer Aniston and Brad Pitt’s marriage was included. This demonstrates the advantage of the interquartile range over the range, i.e. it isn’t affected by extreme scores at either end of the distribution
Chapter 2
Task 2.1
Why do we use samples?
We are usually interested in populations, but because we cannot collect data from every human being (or whatever) in the population, we collect data from a small subset of the population (known as a sample) and use these data to infer things about the population as a whole.
Task 2.2
What is the mean and how do we tell if it’s representative of our data?
The mean is a simple statistical model of the centre of a distribution of scores. A hypothetical estimate of the ‘typical’ score. We use the variance, or standard deviation, to tell us whether it is representative of our data. The standard deviation is a measure of how much error there is associated with the mean: a small standard deviation indicates that the mean is a good representation of our data.
Task 2.3
What’s the difference between the standard deviation and the standard error?
The standard deviation tells us how much observations in our sample differ from the mean value within our sample. The standard error tells us not about how the sample mean represents the sample itself, but how well the sample mean represents the population mean. The standard error is the standard deviation of the sampling distribution of a statistic. For a given statistic (e.g. the mean) it tells us how much variability there is in this statistic across samples from the same population. Large values, therefore, indicate that a statistic from a given sample may not be an accurate reflection of the population from which the sample came.
Task 2.4
In Chapter 1 we used an example of the time in seconds taken for 21 heavy smokers to fall off a treadmill at the fastest setting (18, 16, 18, 24, 23, 22, 22, 23, 26, 29, 32, 34, 34, 36, 36, 43, 42, 49, 46, 46, 57). Calculate standard error and 95% confidence interval for these data.
If you did the tasks in Chapter 1, you’ll know that the mean is 32.19 seconds:
\[ \begin{aligned} \overline{X} &= \frac{\sum_{i=1}^{n} x_i}{n} \\ &= \frac{16+(2\times18)+(2\times22)+(2\times23)+24+26+29+32+(2\times34)+(2\times36)+42+43+(2\times46)+49+57}{21} \\ &= \frac{676}{21} \\ &= 32.19 \end{aligned} \]
We also worked out that the sum of squared errors was 2685.24; the variance was 2685.24/20 = 134.26; the standard deviation is the square root of the variance, so was \(\sqrt(134.26)\) = 11.59. The standard error will be:
\[ SE = \frac{s}{\sqrt{N}} = \frac{11.59}{\sqrt{21}} = 2.53 \]
The sample is small, so to calculate the confidence interval we need to find the appropriate value of t. First we need to calculate the degrees of freedom, \(N − 1\). With 21 data points, the degrees of freedom are 20. For a 95% confidence interval we can look up the value in the column labelled ‘Two-Tailed Test’, ‘0.05’ in the table of critical values of the t-distribution (Appendix). The corresponding value is 2.09. The confidence intervals is, therefore, given by:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(2.09 \times SE)) \\ &= 32.19 – (2.09 × 2.53) \\ & = 26.90 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(2.09 \times SE) \\ &= 32.19 + (2.09 × 2.53) \\ &= 37.48 \end{aligned} \]
Task 2.5
What do the sum of squares, variance and standard deviation represent? How do they differ?
All of these measures tell us something about how well the mean fits the observed sample data. Large values (relative to the scale of measurement) suggest the mean is a poor fit of the observed scores, and small values suggest a good fit. They are also, therefore, measures of dispersion, with large values indicating a spread-out distribution of scores and small values showing a more tightly packed distribution. These measures all represent the same thing, but differ in how they express it. The sum of squared errors is a ‘total’ and is, therefore, affected by the number of data points. The variance is the ‘average’ variability but in units squared. The standard deviation is the average variation but converted back to the original units of measurement. As such, the size of the standard deviation can be compared to the mean (because they are in the same units of measurement).
Task 2.6
What is a test statistic and what does it tell us?
A test statistic is a statistic for which we know how frequently different values occur. The observed value of such a statistic is typically used to test hypotheses, or to establish whether a model is a reasonable representation of what’s happening in the population.
Task 2.7
What are Type I and Type II errors?
A Type I error occurs when we believe that there is a genuine effect in our population, when in fact there isn’t. A Type II error occurs when we believe that there is no effect in the population when, in reality, there is.
Task 2.8
What is statistical power?
Power is the ability of a test to detect an effect of a particular size (a value of 0.8 is a good level to aim for).
Task 2.9
Figure 2.16 shows two experiments that looked at the effect of singing versus conversation on how much time a woman would spend with a man. In both experiments the means were 10 (singing) and 12 (conversation), the standard deviations in all groups were 3, but the group sizes were 10 per group in the first experiment and 100 per group in the second. Compute the values of the confidence intervals displayed in the Figure.
Experiment 1:
In both groups, because they have a standard deviation of 3 and a sample size of 10, the standard error will be:
\[ SE = \frac{s}{\sqrt{N}} = \frac{3}{\sqrt{10}} = 0.95 \]
The sample is small, so to calculate the confidence interval we need to find the appropriate value of t. First we need to calculate the degrees of freedom, \(N − 1\). With 10 data points, the degrees of freedom are 9. For a 95% confidence interval we can look up the value in the column labelled ‘Two-Tailed Test’, ‘0.05’ in the table of critical values of the t-distribution (Appendix). The corresponding value is 2.26. The confidence interval for the singing group is, therefore, given by:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(2.26 \times SE) \\ &= 10 – (2.26 × 0.95) \\ & = 7.85 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(2.26 \times SE) \\ &= 10 + (2.26 × 0.95) \\ &= 12.15 \end{aligned} \]
For the conversation group:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(2.26 \times SE) \\ &= 12 – (2.26 × 0.95) \\ & = 9.85 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(2.26 \times SE) \\ &= 12 + (2.26 × 0.95) \\ &= 14.15 \end{aligned} \]
Experiment 2
In both groups, because they have a standard deviation of 3 and a sample size of 100, the standard error will be:
\[ SE = \frac{s}{\sqrt{N}} = \frac{3}{\sqrt{100}} = 0.3 \]
The sample is large, so to calculate the confidence interval we need to find the appropriate value of z. For a 95% confidence interval we should look up the value of 0.025 in the column labelled Smaller Portion in the table of the standard normal distribution (Appendix). The corresponding value is 1.96. The confidence interval for the singing group is, therefore, given by:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(1.96 \times SE) \\ &= 10 – (1.96 × 0.3) \\ & = 9.41 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(1.96 \times SE) \\ &= 10 + (1.96 × 0.3) \\ &= 10.59 \end{aligned} \]
For the conversation group:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(1.96 \times SE) \\ &= 12 – (1.96 × 0.3) \\ & = 11.41 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(1.96 \times SE) \\ &= 12 + (1.96 × 0.3) \\ &= 12.59 \end{aligned} \]
Task 2.10
Figure 2.17 shows a similar study to above, but the means were 10 (singing) and 10.01 (conversation), the standard deviations in both groups were 3, and each group contained 1 million people. Compute the values of the confidence intervals displayed in the figure.
In both groups, because they have a standard deviation of 3 and a sample size of 1,000,000, the standard error will be:
\[ SE = \frac{s}{\sqrt{N}} = \frac{3}{\sqrt{1000000}} = 0.003 \]
The sample is large, so to calculate the confidence interval we need to find the appropriate value of z. For a 95% confidence interval we should look up the value of 0.025 in the column labelled Smaller Portion in the table of the standard normal distribution (Appendix). The corresponding value is 1.96. The confidence interval for the singing group is, therefore, given by:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(1.96 \times SE) \\ &= 10 – (1.96 × 0.003) \\ & = 9.99412 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(1.96 \times SE) \\ &= 10 + (1.96 × 0.003) \\ &= 10.00588 \end{aligned} \]
For the conversation group:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(1.96 \times SE) \\ &= 10.01 – (1.96 × 0.003) \\ & = 10.00412 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(1.96 \times SE) \\ &= 10.01 + (1.96 × 0.003) \\ &= 10.01588 \end{aligned} \]
Note: these values will look slightly different than the plot because the exact means were 10.00147 and 10.01006, but we rounded off to 10 and 10.01 to make life a bit easier. If you use these exact values you’d get, for the singing group:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(1.96 \times SE) \\ &= 10.01006 – (1.96 × 0.003) \\ & = 9.99559 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(1.96 \times SE) \\ &= 10.01006 + (1.96 × 0.003) \\ &= 10.00735 \end{aligned} \]
For the conversation group:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(1.96 \times SE) \\ &= 10.01006 – (1.96 × 0.003) \\ & = 10.00418 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(1.96 \times SE) \\ &= 10.01006 + (1.96 × 0.003) \\ &= 10.01594 \end{aligned} \]
Task 2.11
In Chapter 1 (Task 8) we looked at an example of how many games it took a sportsperson before they hit the ‘red zone’ Calculate the standard error and confidence interval for those data.
We worked out in Chapter 1 that the mean was 10.27, the standard deviation 4.15, and there were 11 sportspeople in the sample. The standard error will be:
\[ SE = \frac{s}{\sqrt{N}} = \frac{4.15}{\sqrt{11}} = 1.25 \] The sample is small, so to calculate the confidence interval we need to find the appropriate value of t. First we need to calculate the degrees of freedom, \(N − 1\). With 11 data points, the degrees of freedom are 10. For a 95% confidence interval we can look up the value in the column labelled ‘Two-Tailed Test’, ‘.05’ in the table of critical values of the t-distribution (Appendix). The corresponding value is 2.23. The confidence interval is, therefore, given by:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(2.23 \times SE) \\ &= 10.27 – (2.23 × 1.25) \\ & = 7.48 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(2.23 \times SE) \\ &= 10.27 + (2.23 × 1.25) \\ &= 13.06 \end{aligned} \]
Task 2.12
At a rival club to the one I support, they similarly measured the number of consecutive games it took their players before they reached the red zone. The data are: 6, 17, 7, 3, 8, 9, 4, 13, 11, 14, 7. Calculate the mean, standard deviation, and confidence interval for these data.
First we need to compute the mean: \[ \begin{aligned} \overline{X} &= \frac{\sum_{i=1}^{n} x_i}{n} \\ &= \frac{6+17+7+3+8+9+4+13+11+14+7}{11} \\ &= \frac{99}{11} \\ &= 9.00 \end{aligned} \]
Then the standard deviation, which we do as follows:
| Score | Error (score - mean) | Error squared | |
|---|---|---|---|
| 6 | -3 | 9 | |
| 17 | 8 | 64 | |
| 7 | -2 | 4 | |
| 3 | -6 | 36 | |
| 8 | -1 | 1 | |
| 9 | 0 | 0 | |
| 4 | -5 | 25 | |
| 13 | 4 | 16 | |
| 11 | 2 | 4 | |
| 14 | 5 | 25 | |
| 7 | -2 | 4 | |
| Total | — | — | 188 |
The sum of squared errors is:
\[ \begin{aligned} \text{SS} &= 9 + 64 + 4 + 36 + 1 + 0 + 25 + 16 + 4 + 25 + 4 \\ &= 188 \\ \end{aligned} \]
The variance is the sum of squared errors divided by the degrees of freedom:
\[ \begin{aligned} s^2 &= \frac{SS}{N - 1} \\ &= \frac{188}{10} \\ &= 18.8 \end{aligned} \]
The standard deviation is the square root of the variance:
\[ \begin{aligned} s &= \sqrt{s^2} \\ &= \sqrt{18.8} \\ &= 4.34 \end{aligned} \]
There were 11 sportspeople in the sample, so the standard error will be: \[ SE = \frac{s}{\sqrt{N}} = \frac{4.34}{\sqrt{11}} = 1.31\]
The sample is small, so to calculate the confidence interval we need to find the appropriate value of t. First we need to calculate the degrees of freedom, \(N − 1\). With 11 data points, the degrees of freedom are 10. For a 95% confidence interval we can look up the value in the column labelled ‘Two-Tailed Test’, ‘0.05’ in the table of critical values of the t-distribution (Appendix). The corresponding value is 2.23. The confidence intervals is, therefore, given by:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(2.23\times SE)) \\ &= 9 – (2.23 × 1.31) \\ & = 6.08 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(2.23\times SE) \\ &= 9 + (2.23 × 1.31) \\ &= 11.92 \end{aligned} \]
Task 2.13
In Chapter 1 (Task 9) we looked at the length in days of 11 celebrity marriages. Here are the approximate lengths in months of nine marriages, one being mine and the others being those of some of my friends and family. In all but two cases the lengths are calculated up to the day I’m writing this, which is 20 June 2023, but the 3- and 111-month durations are marriages that have ended – neither of these is mine, in case you’re wondering: 3, 144, 267, 182, 159, 152, 693, 50, and 111. Calculate the mean, standard deviation and confidence interval for these data.
First we need to compute the mean:
\[ \begin{aligned} \overline{X} &= \frac{\sum_{i=1}^{n} x_i}{n} \\ &= \frac{3 + 144 + 267 + 182 + 159 + 152 + 693 + 50 + 111}{9} \\ &= \frac{1761}{9} \\ &= 195.67 \end{aligned} \]
Compute the standard deviation as follows:
| Score | Error (score - mean) | Error squared | |
|---|---|---|---|
| 3 | -192.67 | 37121.73 | |
| 144 | -51.67 | 2669.79 | |
| 267 | 71.33 | 5087.97 | |
| 182 | -13.67 | 186.87 | |
| 159 | -36.67 | 1344.69 | |
| 152 | -43.67 | 1907.07 | |
| 693 | 497.33 | 247337.13 | |
| 50 | -145.67 | 21219.75 | |
| 111 | -84.67 | 7169.01 | |
| Total | — | — | 324044 |
The sum of squared errors is:
\[ \begin{aligned} \text{SS} &= 37121.73 + 2669.79 + 5087.97 + 186.87 + 1344.69 + 1907.07 + 247337.13 + 21219.75 + 7169.01 \\ &= 324044 \\ \end{aligned} \]
The variance is the sum of squared errors divided by the degrees of freedom:
\[ \begin{aligned} s^2 &= \frac{SS}{N - 1} \\ &= \frac{324044}{8} \\ &= 40505.5 \end{aligned} \] The standard deviation is the square root of the variance:
\[ \begin{aligned} s &= \sqrt{s^2} \\ &= \sqrt{40505.5} \\ &= 201.2598 \end{aligned} \]
The standard error is:
\[ \begin{aligned} SE &= \frac{s}{\sqrt{N}} \\ &= \frac{201.2598}{\sqrt{9}} \\ &= 67.0866 \end{aligned} \]
The sample is small, so to calculate the confidence interval we need to find the appropriate value of t. First we need to calculate the degrees of freedom, \(N − 1\). With 9 data points, the degrees of freedom are 8. For a 95% confidence interval we can look up the value in the column labelled ‘Two-Tailed Test’, ‘0.05’ in the table of critical values of the t-distribution (Appendix). The corresponding value is 2.31. The confidence interval is, therefore, given by:
\[ \begin{aligned} \text{95% CI}_\text{lower boundary} &= \overline{X}-(2.31 \times SE)) \\ &= 195.67 – (2.31 × 67.0866) \\ & = 40.70 \\ \text{95% CI}_\text{upper boundary} &= \overline{X}+(2.31 \times SE) \\ &= 195.67 + (2.31 × 67.0866) \\ &= 350.64 \end{aligned} \]
Chapter 3
Task 3.1
What is an effect size and how is it measured?
An effect size is an objective and standardized measure of the magnitude of an observed effect. Measures include Cohen’s d, the odds ratio and Pearson’s correlations coefficient, r. Cohen’s d, for example, is the difference between two means divided by either the standard deviation of the control group, or by a pooled standard deviation.
Task 3.2
In Chapter 1 (Task 8) we looked at an example of how many games it took a sportsperson before they hit the ‘red zone’, then in Chapter 2 we looked at data from a rival club. Compute and interpret Cohen’s \(\hat{d}\) for the difference in the mean number of games it took players to become fatigued in the two teams mentioned in those tasks.
Cohen’s d is defined as:
\[ \hat{d} = \frac{\bar{X_1}-\bar{X_2}}{s} \]
There isn’t an obvious control group, so let’s use a pooled estimate of the standard deviation:
\[ \begin{aligned} s_p &= \sqrt{\frac{(N_1-1) s_1^2+(N_2-1) s_2^2}{N_1+N_2-2}} \\ &= \sqrt{\frac{(11-1)4.15^2+(11-1)4.34^2}{11+11-2}} \\ &= \sqrt{\frac{360.23}{20}} \\ &= 4.24 \end{aligned} \]
Therefore, Cohen’s \(\hat{d}\) is:
\[ \hat{d} = \frac{10.27-9}{4.24} = 0.30 \]
Therefore, the second team fatigued in fewer matches than the first team by about 1/3 standard deviation. By the benchmarks that we probably shouldn’t use, this is a small to medium effect, but I guess if you’re managing a top-flight sports team, fatiguing 1/3 of a standard deviation faster than one of your opponents could make quite a substantial difference to your performance and team rotation over the season.
Task 3.3
Calculate and interpret Cohen’s \(\hat{d}\) for the difference in the mean duration of the celebrity marriages in Chapter 1 (Task 9) and me and my friend’s marriages (Chapter 2, Task 13).
Cohen’s \(\hat{d}\) is defined as:
\[ \hat{d} = \frac{\bar{X_1}-\bar{X_2}}{s} \]
There isn’t an obvious control group, so let’s use a pooled estimate of the standard deviation:
\[ \begin{aligned} s_p &= \sqrt{\frac{(N_1-1) s_1^2+(N_2-1) s_2^2}{N_1+N_2-2}} \\ &= \sqrt{\frac{(11-1)476.29^2+(9-1)8275.91^2}{11+9-2}} \\ &= \sqrt{\frac{550194093}{18}} \\ &= 5528.68 \end{aligned} \]
Therefore, Cohen’s d is: \[\hat{d} = \frac{5057-238.91}{5528.68} = 0.87\] Therefore, my friend’s marriages are 0.87 standard deviations longer than the sample of celebrities. By the benchmarks that we probably shouldn’t use, this is a large effect.
Task 3.4
What are the problems with null hypothesis significance testing?
- We can’t conclude that an effect is important because the p-value from which we determine significance is affected by sample size. Therefore, the word ‘significant’ is meaningless when referring to a p-value.
- The null hypothesis is never true. If the p-value is greater than .05 then we can decide to reject the alternative hypothesis, but this is not the same thing as the null hypothesis being true: a non-significant result tells us is that the effect is not big enough to be found but it doesn’t tell us that the effect is zero.
- A significant result does not tell us that the null hypothesis is false (see text for details).
- It encourages all or nothing thinking: if p < 0.05 then an effect is significant, but if p > 0.05 it is not. So, a p = 0.0499 is significant but a p = 0.0501 is not, even though these ps differ by only 0.0002.
Task 3.5
What is the difference between a confidence interval and a credible interval?
A 95% confidence interval is set so that before the data are collected there is a long-run probability of 0.95 (or 95%) that the interval will contain the true value of the parameter. This means that in 100 random samples, the intervals will contain the true value in 95 of them but won’t in 5. Once the data are collected, your sample is either one of the 95% that produces an interval containing the true value, or one of the 5% that does not. In other words, having collected the data, the probability of the interval containing the true value of the parameter is either 0 (it does not contain it) or 1 (it does contain it), but you do not know which. A credible interval is different in that it reflects the plausible probability that the interval contains the true value. For example, a 95% credible interval has a plausible 0.95 probability of containing the true value.
Task 3.6
What is a meta-analysis?
Meta-analysis is where effect sizes from different studies testing the same hypothesis are combined to get a better estimate of the size of the effect in the population.
Task 3.7
Describe what you understand by the term Bayes factor.
The Bayes factor is the ratio of the probability of the data given the alternative hypothesis to that of the data given the null hypothesis. A Bayes factor less than 1 supports the null hypothesis (it suggests the data are more likely given the null hypothesis than the alternative hypothesis); conversely, a Bayes factor greater than 1 suggests that the observed data are more likely given the alternative hypothesis than the null. Values between 1 and 3 are considered evidence for the alternative hypothesis that is ‘barely worth mentioning’, values between 3 and 10 are considered to indicate evidence for the alternative hypothesis that ‘has substance’, and values greater than 10 are strong evidence for the alternative hypothesis.
Task 3.8
Various studies have shown that students who use laptops in class often do worse on their modules (Payne-Carter, Greenberg, & Walker, 2016; Sana, Weston, & Cepeda, 2013). Table 3.3 (reproduced in in Table 8) shows some fabricated data that mimics what has been found. What is the odds ratio for passing the exam if the student uses a laptop in class compared to if they don’t?
| Laptop | No Laptop | Sum | |
|---|---|---|---|
| Pass | 24 | 49 | 73 |
| Fail | 16 | 11 | 27 |
| Sum | 40 | 60 | 100 |
First we compute the odds of passing when a laptop is used in class:
\[ \begin{aligned} \text{Odds}_{\text{pass when laptop is used}} &= \frac{\text{Number of laptop users passing exam}}{\text{Number of laptop users failing exam}} \\ &= \frac{24}{16} \\ &= 1.5 \end{aligned} \]
Next we compute the odds of passing when a laptop is not used in class:
\[ \begin{aligned} \text{Odds}_{\text{pass when laptop is not used}} &= \frac{\text{Number of students without laptops passing exam}}{\text{Number of students without laptops failing exam}} \\ &= \frac{49}{11} \\ &= 4.45 \end{aligned} \]
The odds ratio is the ratio of the two odds that we have just computed:
\[ \begin{aligned} \text{Odds Ratio} &= \frac{\text{Odds}_{\text{pass when laptop is used}}}{\text{Odds}_{\text{pass when laptop is not used}}} \\ &= \frac{1.5}{4.45} \\ &= 0.34 \end{aligned} \]
The odds of passing when using a laptop are 0.34 times those when a laptop is not used. If we take the reciprocal of this, we could say that the odds of passing when not using a laptop are 2.97 times those when a laptop is used.
Task 3.9
From the data in Table 3.1 (reproduced in Table 8) what is the conditional probability that someone used a laptop given that they passed the exam, p(laptop|pass). What is the conditional probability of that someone didn’t use a laptop in class given they passed the exam, p(no laptop |pass)?
The conditional probability that someone used a laptop given they passed the exam is 0.33, or a 33% chance:
\[ p(\text{laptop|pass})=\frac{p(\text{laptop ∩ pass})}{p(\text{pass})}=\frac{{24}/{100}}{{73}/{100}}=\frac{0.24}{0.73}=0.33 \]
The conditional probability that someone didn’t use a laptop in class given they passed the exam is 0.67 or a 67% chance.
\[ p(\text{no laptop|pass})=\frac{p(\text{no laptop ∩ pass})}{p(\text{pass})}=\frac{{49}/{100}}{{73}/{100}}=\frac{0.49}{0.73}=0.67 \]
Task 3.10
Using the data in Table 3.1 (reproduced in Table 8), what are the posterior odds of someone using a laptop in class (compared to not using one) given that they passed the exam?
The posterior odds are the ratio of the posterior probability for one hypothesis to another. In this example it would be the ratio of the probability that a used a laptop given that they passed (which we have already calculated above to be 0.33) to the probability that they did not use a laptop in class given that they passed (which we have already calculated above to be 0.67). The value turns out to be 0.49, which means that the probability that someone used a laptop in class if they passed the exam is about half of the probability that someone didn’t use a laptop in class given that they passed the exam.
\[ \text{posterior odds}= \frac{p(\text{hypothesis 1|data})}{p(\text{hypothesis 2|data})} = \frac{p(\text{laptop|pass})}{p(\text{no laptop| pass})} = \frac{0.33}{0.67} = 0.49 \]
Chapter 4
Task 4.1
No answer required.
Task 4.2
What are these icons shortcuts to:
-
 : This icon displays a list of the last 12 dialog boxed that you used.
: This icon displays a list of the last 12 dialog boxed that you used. -
 : Opens the Go To dialog box so that you can skip to a particular variable.
: Opens the Go To dialog box so that you can skip to a particular variable. -
 : Produces descriptive statistics for the currently selected variable or variables in the data editor.
: Produces descriptive statistics for the currently selected variable or variables in the data editor. -
 : This icon opens a dialog box for exporting the contents of the viewer.
: This icon opens a dialog box for exporting the contents of the viewer. -
 : Produces a list of variables in the data editor and summary information about each one.
: Produces a list of variables in the data editor and summary information about each one. -
 : In the syntax window this icon runs the currently selected syntax.
: In the syntax window this icon runs the currently selected syntax. -
 : This icon opens the split file dialog box, which is used to repeat SPSS procedures on different groups/categories separately.
: This icon opens the split file dialog box, which is used to repeat SPSS procedures on different groups/categories separately. -
 : This icon toggles between value labels and numeric codes in the data editor
: This icon toggles between value labels and numeric codes in the data editor
Task 4.3
The data below show the score (out of 20) for 20 different students, some of whom are male and some female, and some of whom were taught using positive reinforcement (being nice) and others who were taught using punishment (electric shock). Enter these data into SPSS and save the file as
teach_method.sav. (Clue: the data should not be entered in the same way that they are laid out below.)
The data can be found in the file teach_method.sav and should look like this:
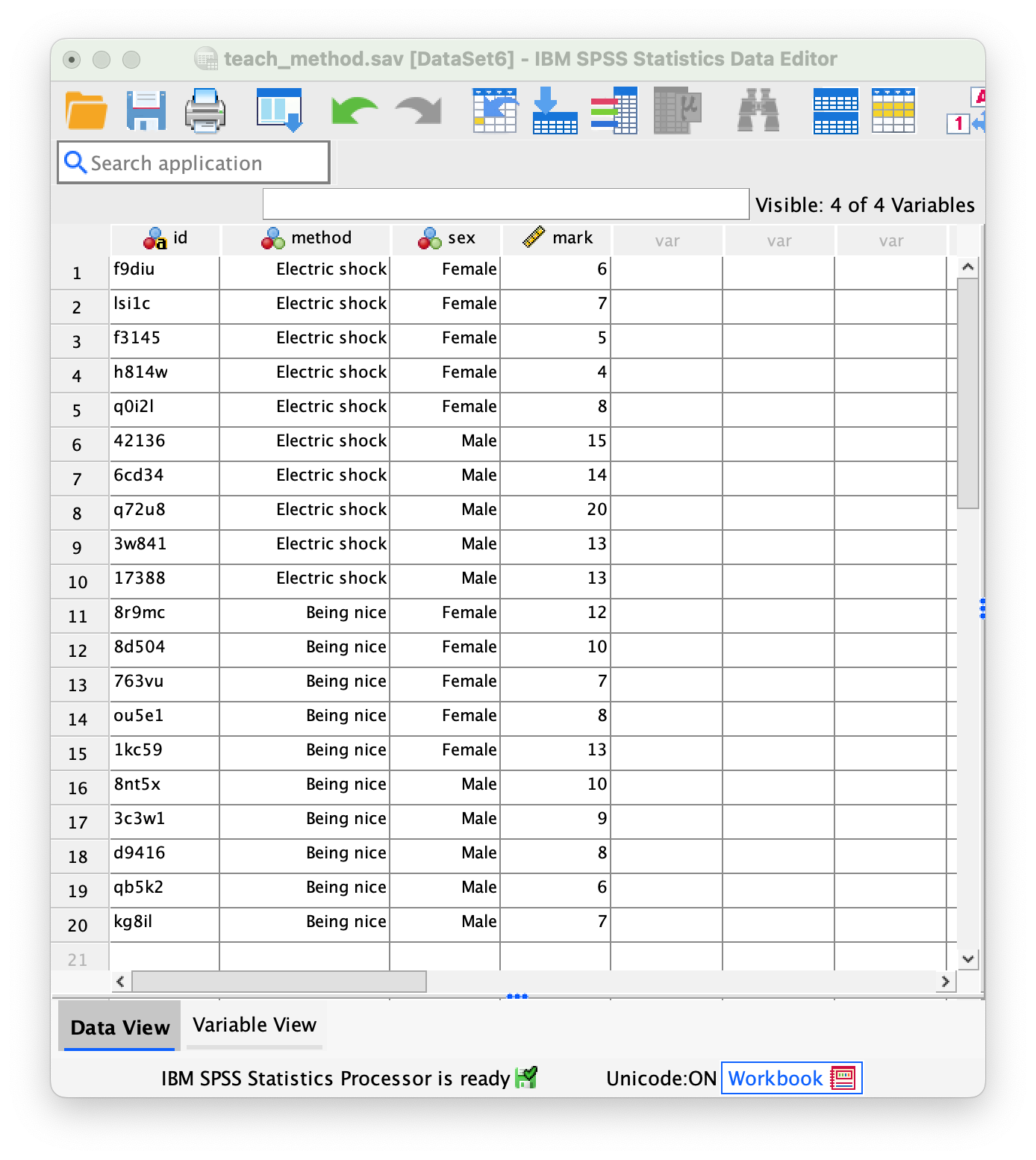
Or with the value labels off, like this:
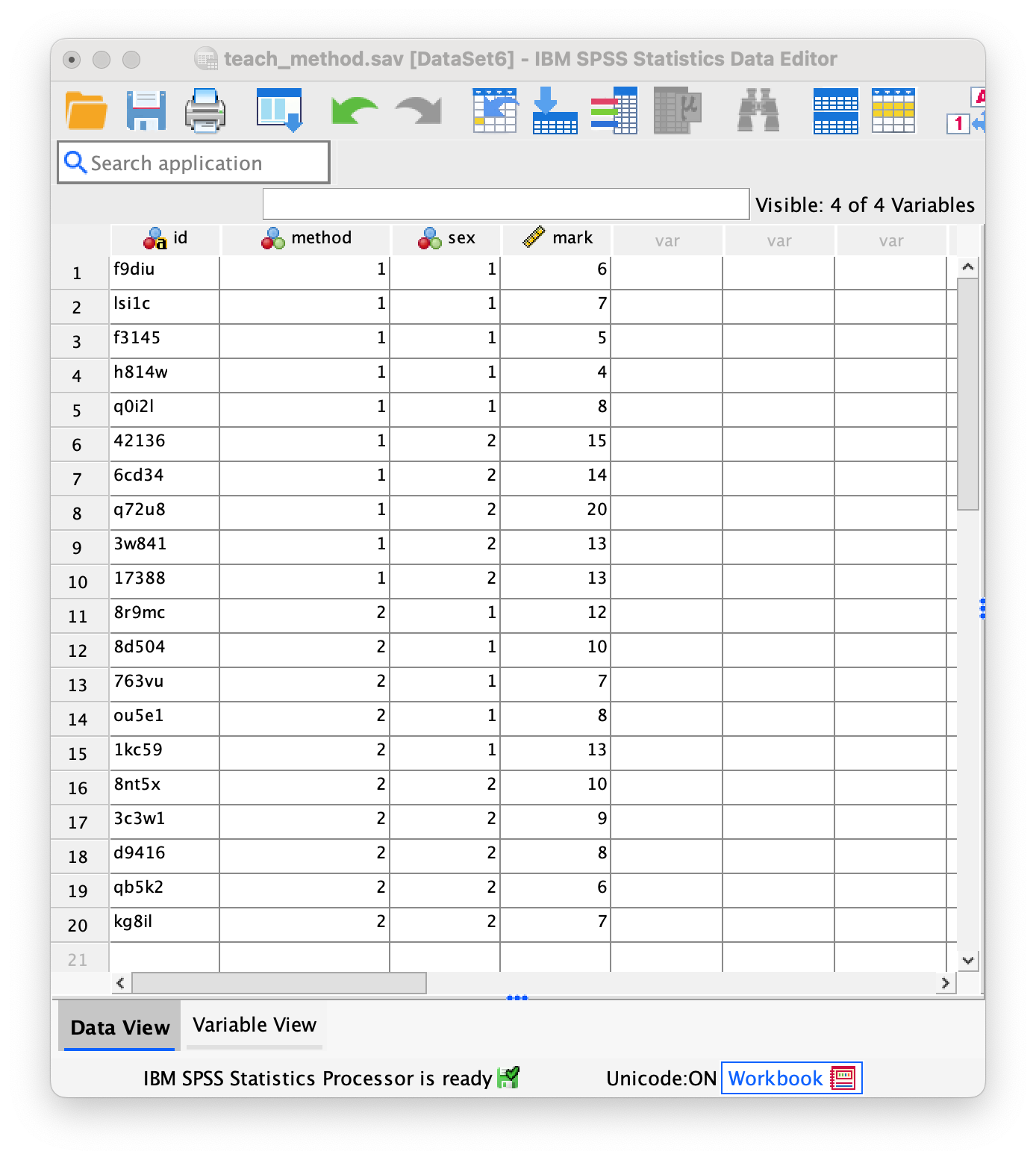
Task 4.4
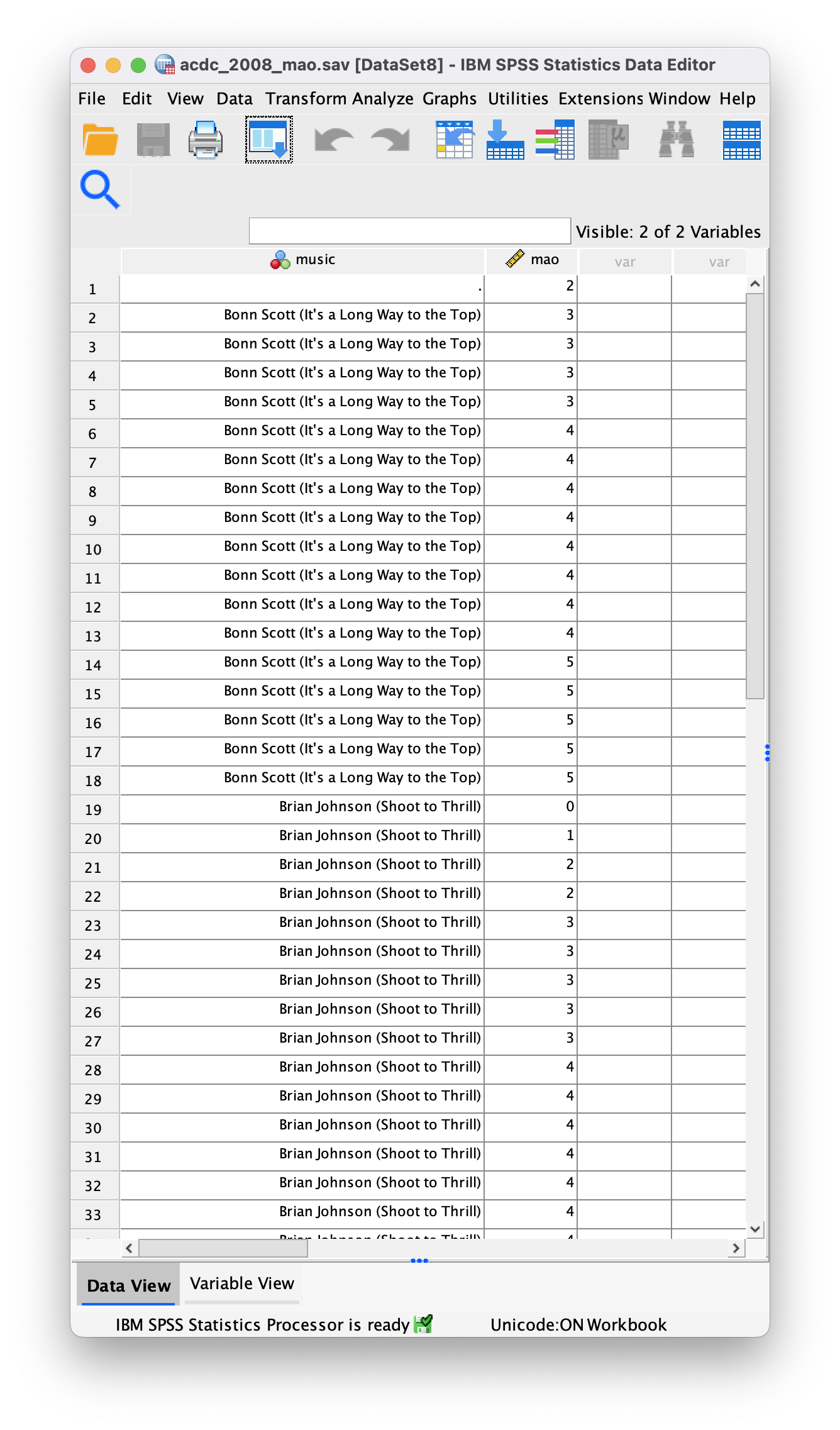
Thinking back to Labcoat Leni’s Real Research 3.1, Oxoby (2008) also measured the minimum acceptable offer; these MAOs (in dollars) are below (again, these are approximations based on the plots in the paper). Enter these data into the SPSS data editor and save this file as
acdc.sav.
- Bon Scott group: 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5
- Brian Johnson group: 0, 1, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 1
The data can be found in the file acdc.sav and should look like this:
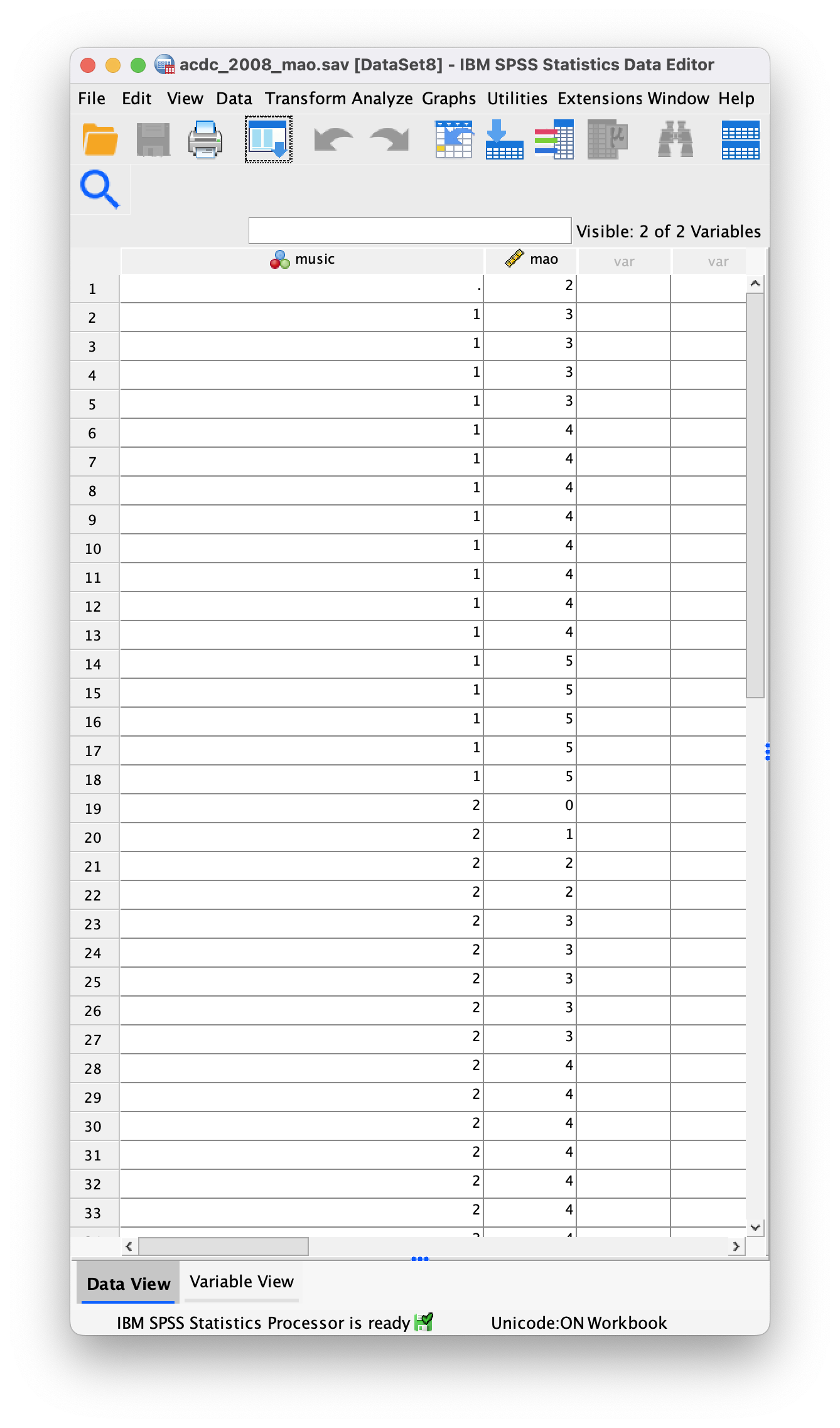
Or with the value labels off, like this:
Task 4.5
According to some highly unscientific research done by a UK department store chain and reported in Marie Clare magazine https://tinyurl.com/mcsgh shopping is good for you: they found that the average women spends 150 minutes and walks 2.6 miles when she shops, burning off around 385 calories. In contrast, men spend only about 50 minutes shopping, covering 1.5 miles. This was based on strapping a pedometer on a mere 10 participants. Although I don’t have the actual data, some simulated data based on these means are below. Enter these data into SPSS and save them as
shopping.sav.
The data can be found in the file shopping.sav and should look like this:
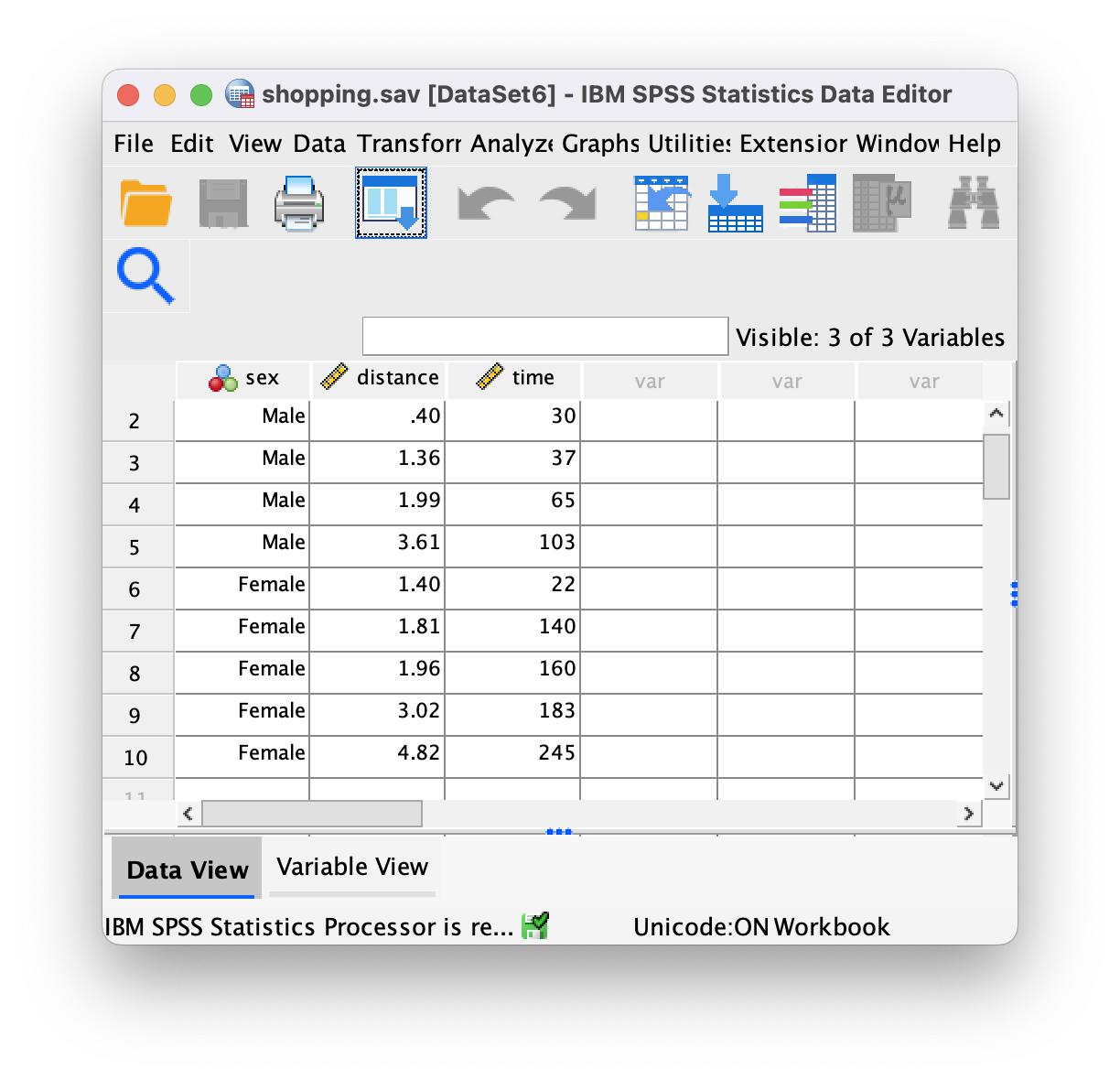
Or with the value labels off, like this:
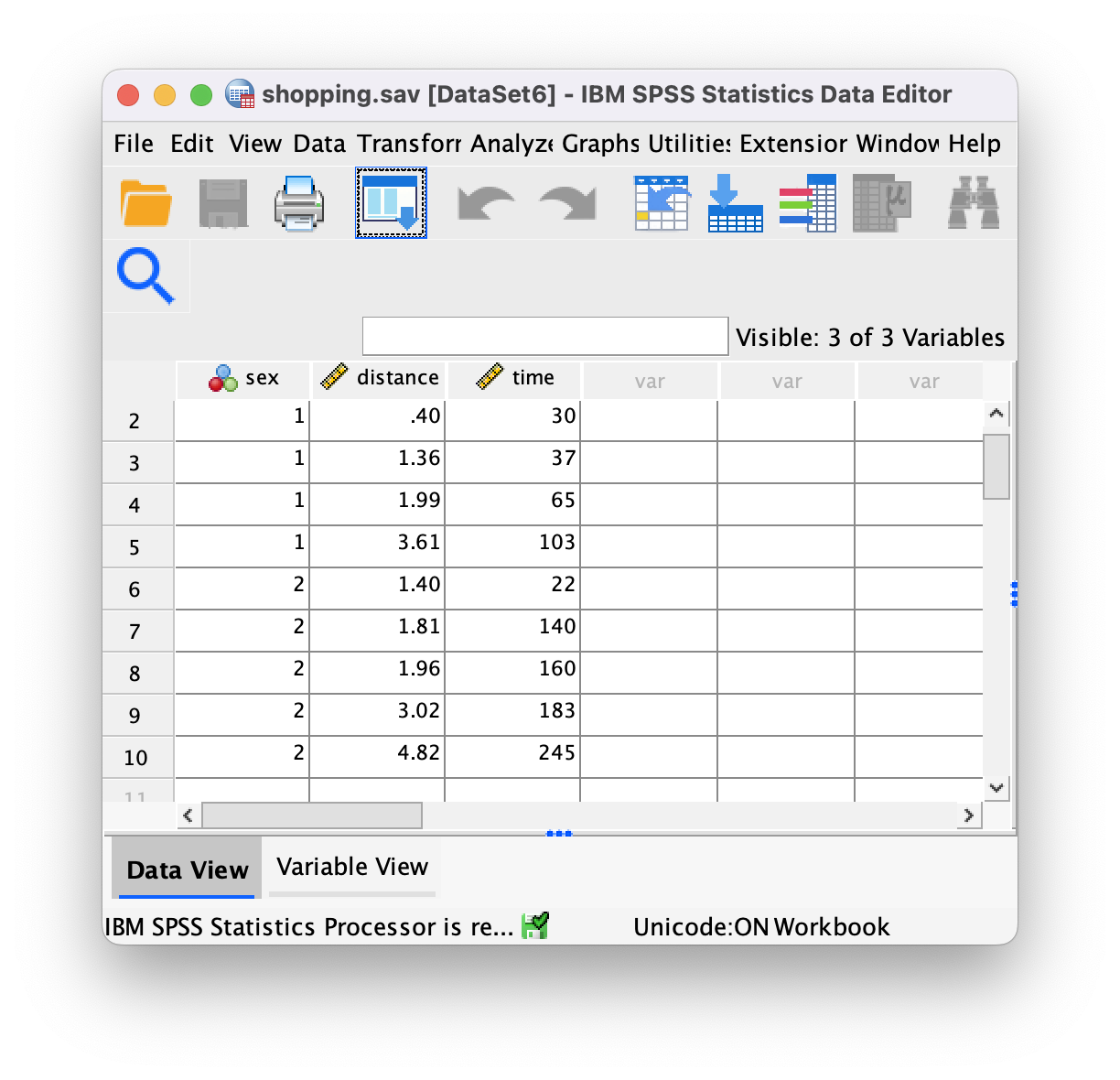
Task 4.6
I wondered whether a fish or cat made a better pet. I found some people who had either fish or cats as pets and measured their life satisfaction and how much they like animals. Enter these data into SPSS and save as
pets.sav.
The data can be found in the file pets.sav and should look like this:
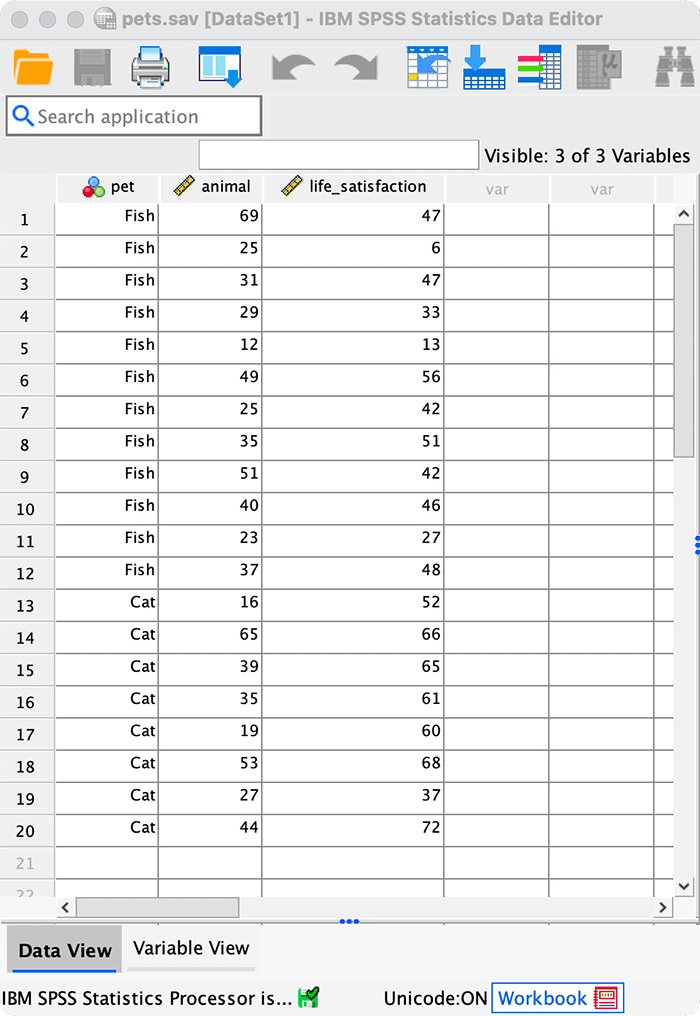
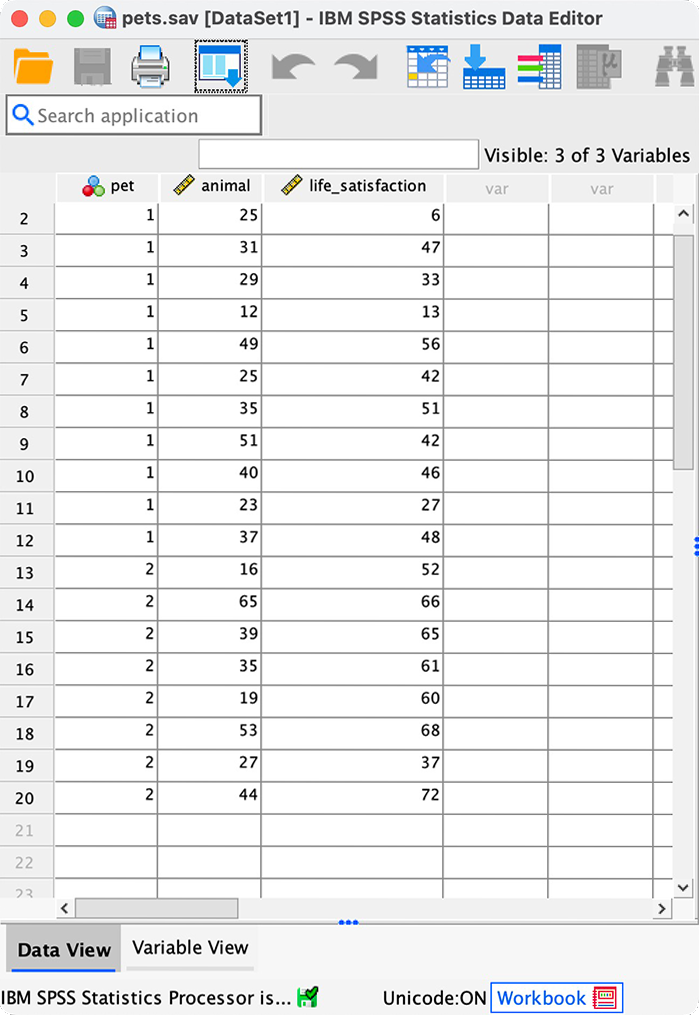
Or with the value labels off, like this:
Task 4.7
One of my favourite activities, especially when trying to do brain-melting things like writing statistics books, is drinking tea. I am English, after all. Fortunately, tea improves your cognitive function, well, in older Chinese people at any rate (Feng et al., 2010). I may not be Chinese and I’m not that old, but I nevertheless enjoy the idea that tea might help me think. Here’s some data based on Feng et al.’s study that measured the number of cups of tea drunk and cognitive functioning in 15 people. Enter these data in SPSS and save the file as
tea_15.sav.
The data can be found in the file tea_15.sav and should look like this:
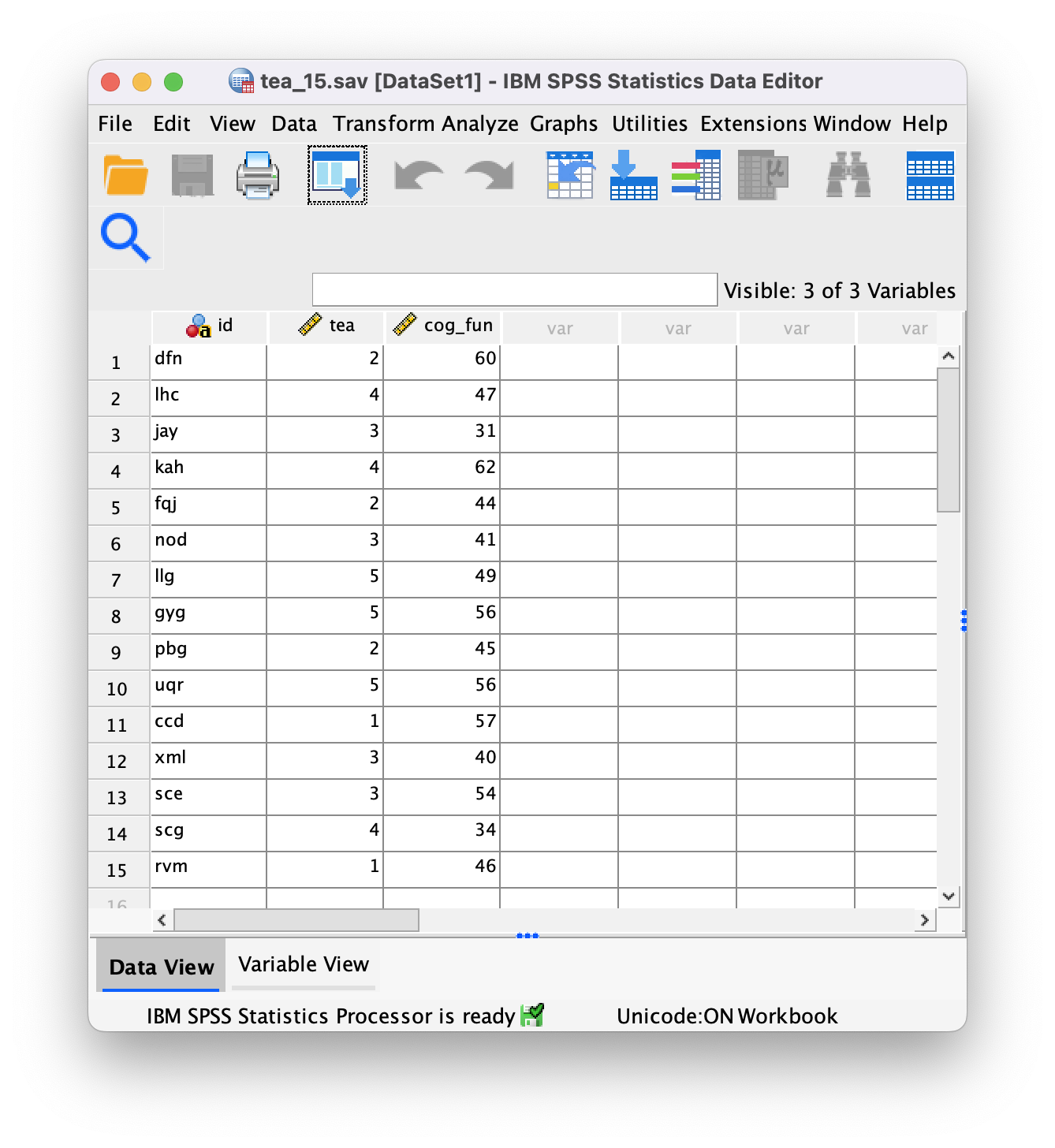
Task 4.8
Statistics and maths anxiety are common and affect people’s performance on maths and stats assignments; women in particular can lack confidence in mathematics (Field, 2010, 2014). Zhang et al. (2013) did an intriguing study in which students completed a maths test in which some put their own name on the test booklet, whereas others were given a booklet that already had either a male or female name on. Participants in the latter two conditions were told that they would use this other person’s name for the purpose of the test. Women who completed the test using a different name performed better than those who completed the test using their own name. (There were no such effects for men.) The data below are a random subsample of Zhang et al.’s data. Enter them into SPSS and save the file as
zhang_sample.sav
The correct format is as in the file zhang_sample.sav on the companion website. The data editor should look like this:
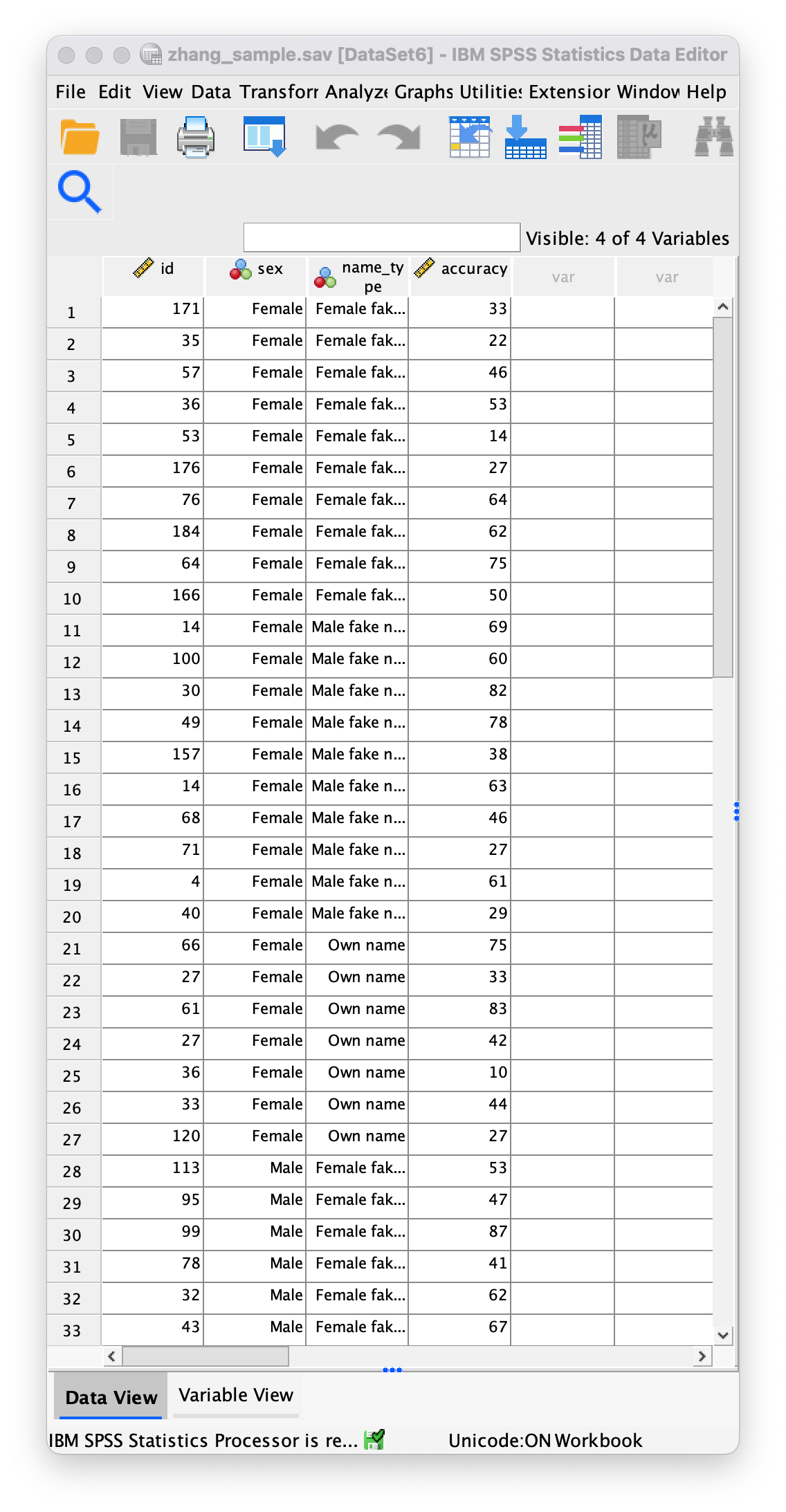
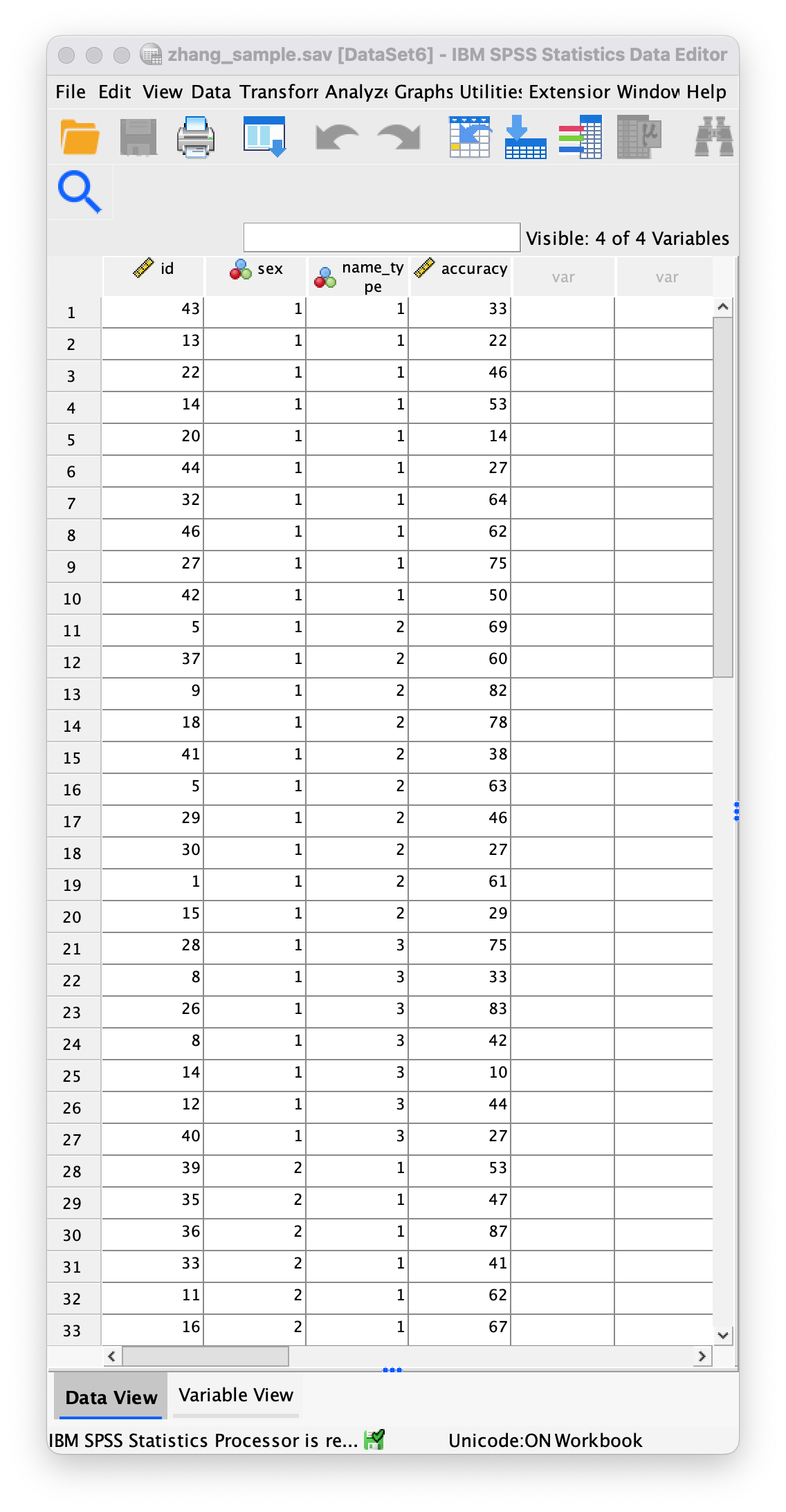
Or with the value labels off, like this:
Task 4.9
What is a coding variable?
A variable in which numbers are used to represent group or category membership. An example would be a variable in which a score of 2 represents a person identifying as non-binary, a 1 represents a person identifying as female, and a 0 represents a person identifying as male.
Task 4.10
What is the difference between wide and long format data?
Long format data are arranged such that scores on an outcome variable appear in a single column and rows represent a combination of the attributes of those scores (for example, the entity from which the scores came, when the score was recorded etc.). In long format data, scores from a single entity can appear over multiple rows where each row represents a combination of the attributes of the score (e.g., levels of an independent variable or time point at which the score was recorded etc.). In contrast, wide format data are arranged such that scores from a single entity appear in a single row and levels of independent or predictor variables are arranged over different columns. As such, in designs with multiple measurements of an outcome variable, for each case the outcome variable scores will be spread across multiple columns with each column containing the score for one level of an independent variable, or for the time point at which the score was observed. Columns can also represent attributes of the score or entity that are fixed over the duration of data collection (e.g., participant sex, employment status etc.).
Chapter 5
Task 5.1
The file
students.savcontains data relating to groups of students and lecturers. Using these data plot and interpret an error bar chart showing the mean number of friends that students and lecturers have.
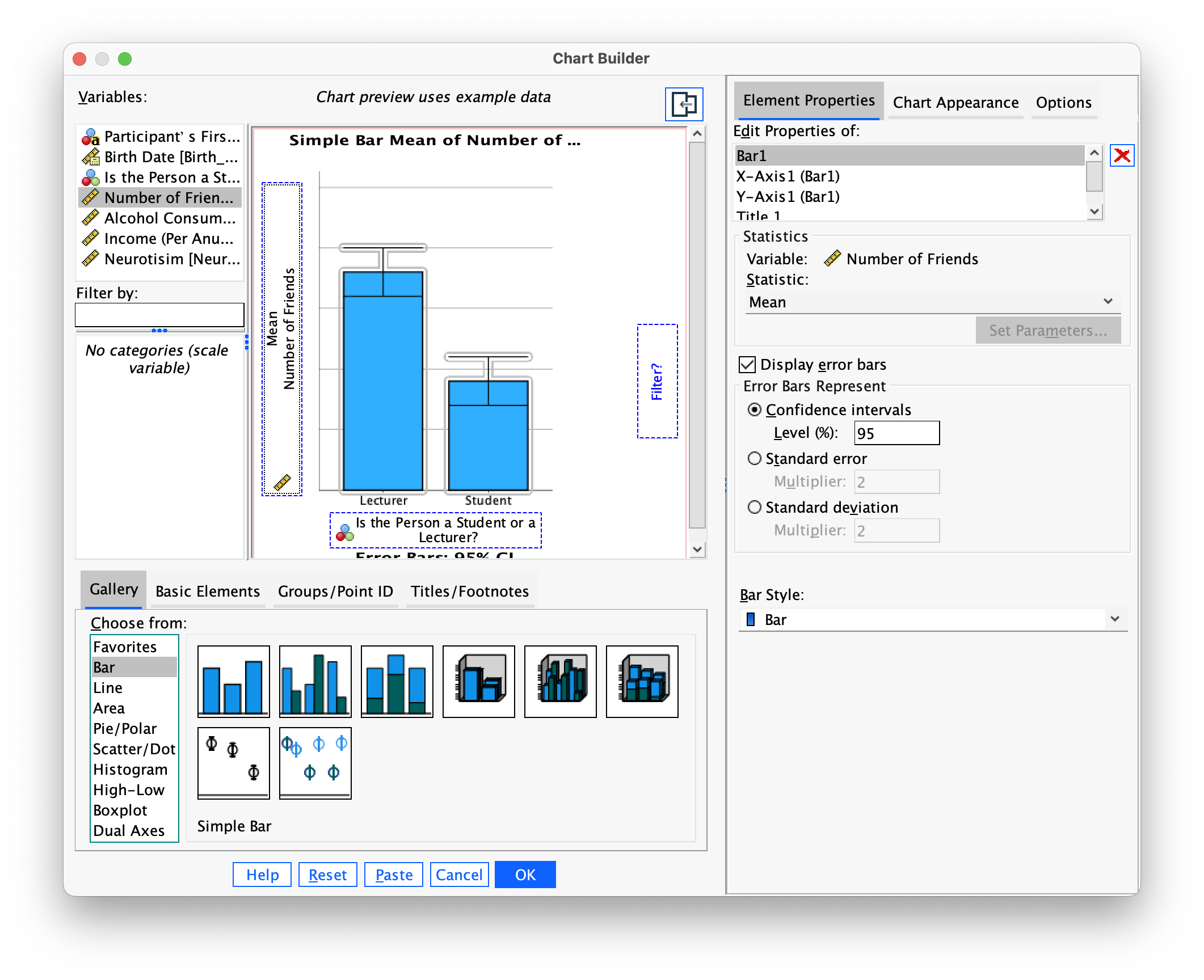
First of all access the chart builder and select a simple bar chart. The y-axis needs to be the dependent variable, or the thing you’ve measured, or more simply the thing for which you want to display the mean. In this case it would be Friends, so drag this variable from the variable list into the  drop zone. The x-axis should be the variable by which we want to split the arousal data. To plot the means for the students and lecturers, drag the variable
drop zone. The x-axis should be the variable by which we want to split the arousal data. To plot the means for the students and lecturers, drag the variable Group from the variable list to the drop zone for the x-axis ( ). Then add error bars by selecting
). Then add error bars by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
The error bar chart will look like this:
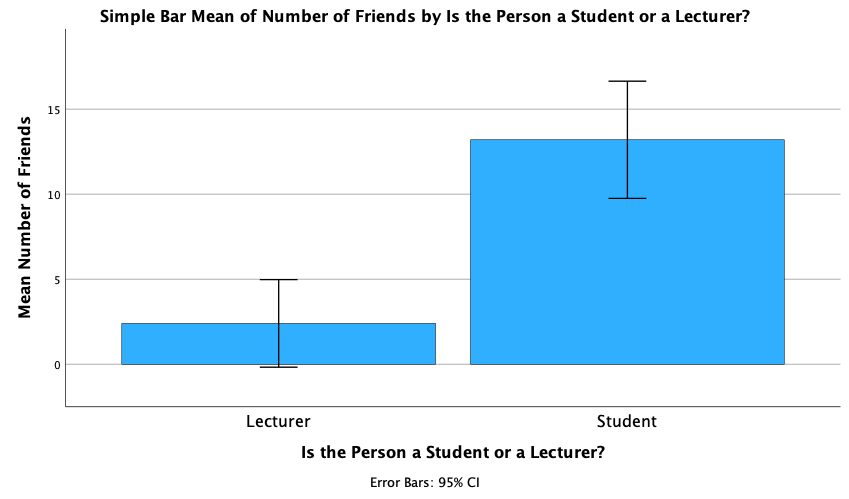
We can conclude that, on average, students had more friends than lecturers.
Task 5.2
Using the same data, plot and interpret an error bar chart showing the mean alcohol consumption for students and lecturers.
Access the chart builder and select a simple bar chart. The y-axis needs to be the thing we’ve measured, which in this case is Alcohol, so drag this variable from the variable list and to the  drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for the students and lecturers, drag the variable
drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for the students and lecturers, drag the variable Group from the variable list to the drop zone for the x-axis ( ). Add error bars by selecting
). Add error bars by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
The error bar chart will look like this:
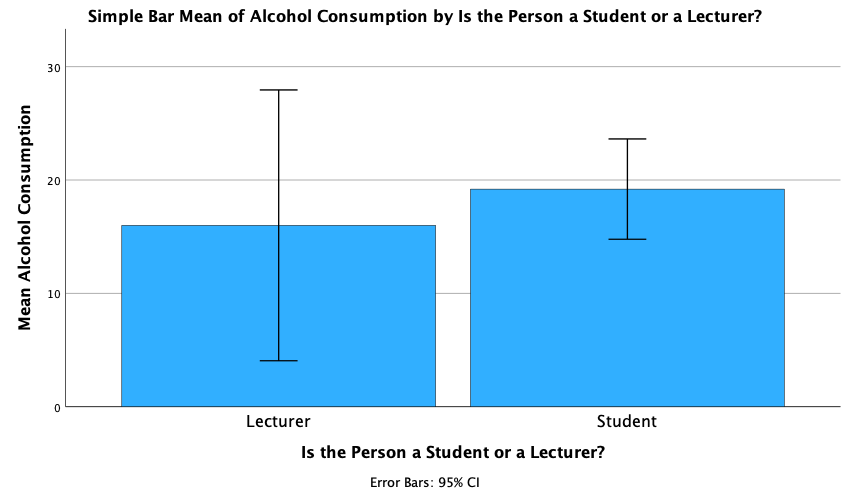
We can conclude that, on average, students and lecturers drank similar amounts, but the error bars tell us that the mean is a better representation of the population for students than for lecturers (there is more variability in lecturers’ drinking habits compared to students’).
Task 5.3
Using the same data, plot and interpret an error line chart showing the mean income for students and lecturers.
Access the chart builder and select a simple line chart. The y-axis needs to be the thing we’ve measured, which in this case is Income, so drag this variable from the variable list to the  drop zone. The x-axis should again be students vs. lecturers, so drag the variable
drop zone. The x-axis should again be students vs. lecturers, so drag the variable Group from the variable list to the drop zone for the x-axis ( ). Add error bars by selecting
). Add error bars by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
The error line chart will look like this:
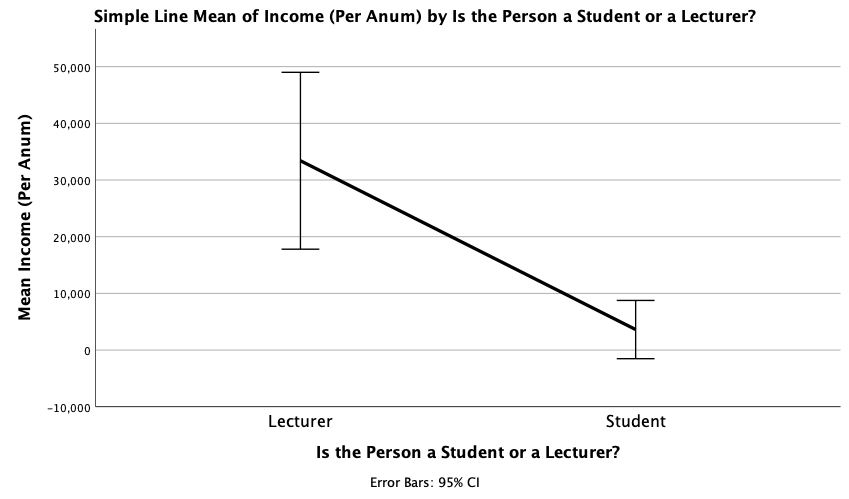
We can conclude that, on average, students earn less than lecturers, but the error bars tell us that the mean is a better representation of the population for students than for lecturers (there is more variability in lecturers’ income compared to students’).
Task 5.4
Using the same data, plot and interpret error a line chart showing the mean neuroticism for students and lecturers.
Access the chart builder and select a simple line chart. The y-axis needs to be the thing we’ve measured, which in this case is Neurotic, so drag this variable from the variable list to the  drop zone. The x-axis should again be students vs. lecturers, so drag the variable
drop zone. The x-axis should again be students vs. lecturers, so drag the variable Group from the variable list to the drop zone for the x-axis ( ). Add error bars by selecting
). Add error bars by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
The error line chart will look like this:
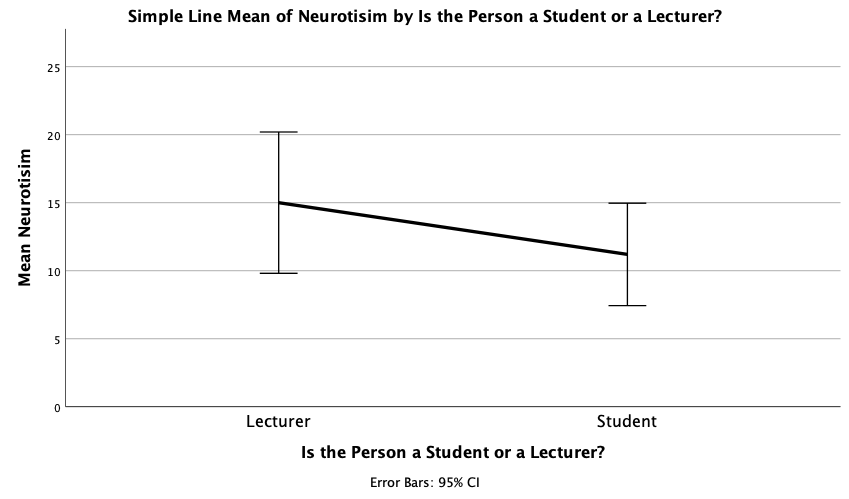
We can conclude that, on average, students are slightly less neurotic than lecturers.
Task 5.5
Using the same data, plot and interpret a scatterplot with regression lines of alcohol consumption and neuroticism grouped by lecturer/student.
Access the chart builder and select a grouped scatterplot. It doesn’t matter which way around we plot these variables, so let’s drag Alcohol from the variable list to the y-axis drop zone, and then drag Neurotic from the variable list and drag it into the drop zone. We then need to split the scatterplot by our grouping variable (lecturers or students), so drag Group to the  drop zone. The completed chart builder dialog box will look like this:
drop zone. The completed chart builder dialog box will look like this:
Click on  to produce the plot. To fit the regression lines double-click on the plot in the SPSS Viewer to open it in the SPSS Chart Editor. Then click on
to produce the plot. To fit the regression lines double-click on the plot in the SPSS Viewer to open it in the SPSS Chart Editor. Then click on ![]() in the chart editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on
in the chart editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on  to fit the lines:
to fit the lines:
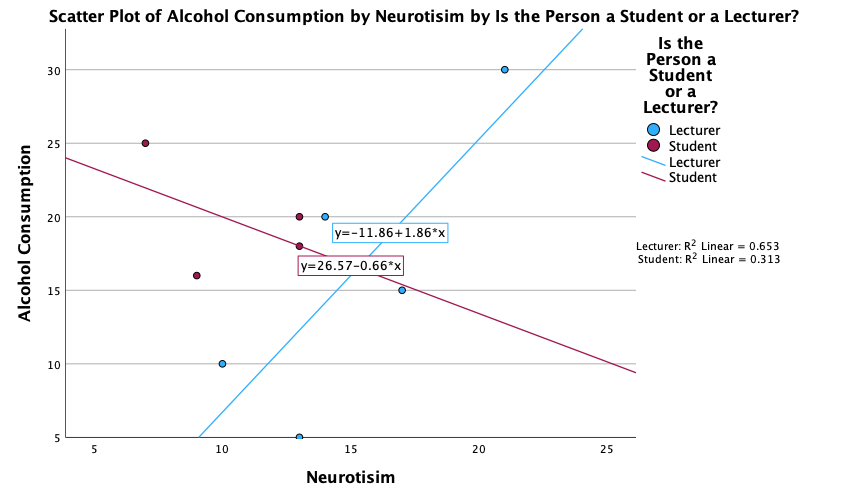
We can conclude that for lecturers, as neuroticism increases so does alcohol consumption (a positive relationship), but for students the opposite is true, as neuroticism increases alcohol consumption decreases. Note that SPSS has scaled this plot oddly because neither axis starts at zero; as a bit of extra practice, why not edit the two axes so that they start at zero? You can do this by first double-clicking on the x-axis to activate the properties dialog box and then in the custom box set the minimum to be 0 instead of 5. Repeat this process for the y-axis. The resulting plot will look like this:
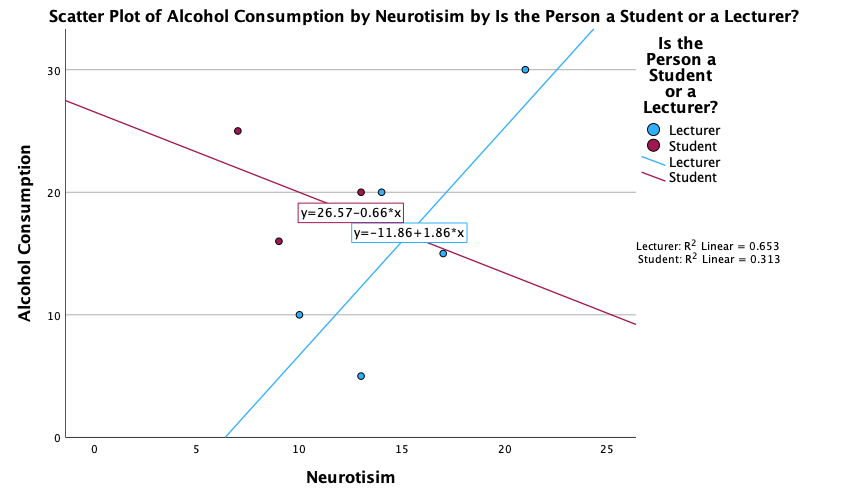
Task 5.6
Using the same data, plot and interpret a scatterplot matrix with regression lines of alcohol consumption, neuroticism and number of friends.
Access the chart builder and select a scatterplot matrix. We have to drag all three variables into the  drop zone. Select the first variable (
drop zone. Select the first variable (Friends) by clicking on it with the mouse. Now, hold down the Ctrl (Cmd on a Mac) key on the keyboard and click on a second variable (Alcohol). Finally, hold down the Ctrl (or Cmd) key and click on a third variable (Neurotic). Once the three variables are selected, click on any one of them and then drag them into the  drop zone. The completed dialog box will look like this:
drop zone. The completed dialog box will look like this:
Click on  to produce the plot. To fit the regression lines double-click on the plot in the SPSS Viewer to open it in the SPSS Chart Editor. Then click on
to produce the plot. To fit the regression lines double-click on the plot in the SPSS Viewer to open it in the SPSS Chart Editor. Then click on ![]() in the Chart Editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on
in the Chart Editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on  to fit the lines. The resulting plot looks like this:
to fit the lines. The resulting plot looks like this:
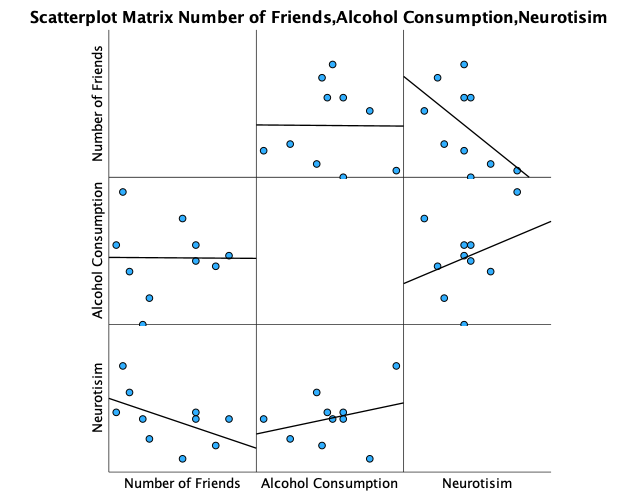
We can conclude that there is no relationship (flat line) between the number of friends and alcohol consumption; there was a negative relationship between how neurotic a person was and their number of friends (line slopes downwards); and there was a slight positive relationship between how neurotic a person was and how much alcohol they drank (line slopes upwards).
Task 5.7
Using the
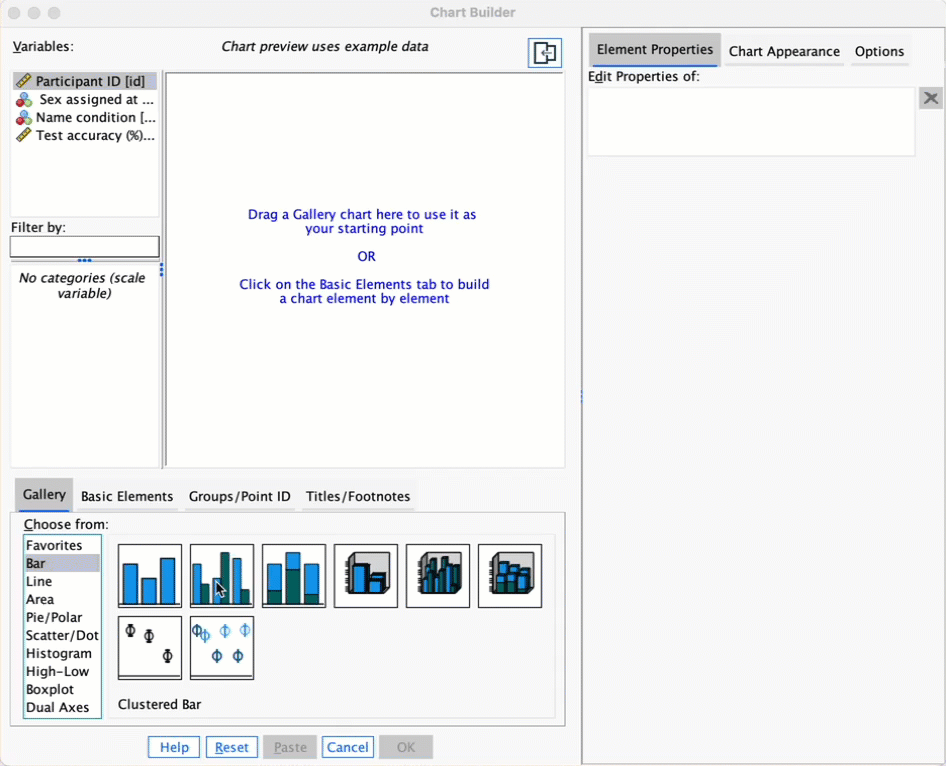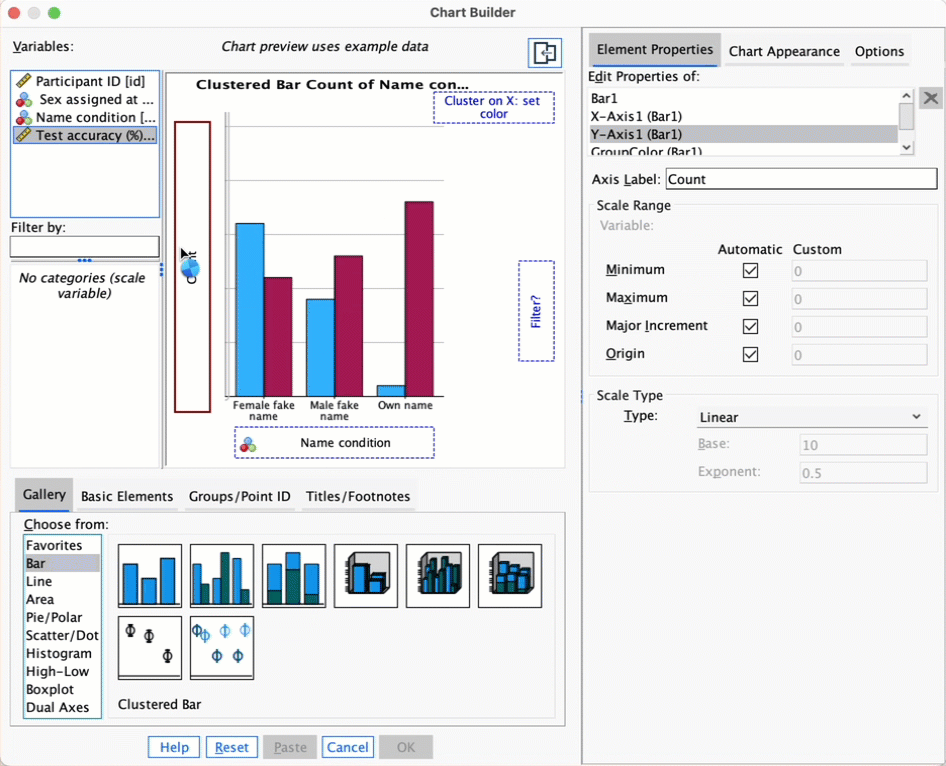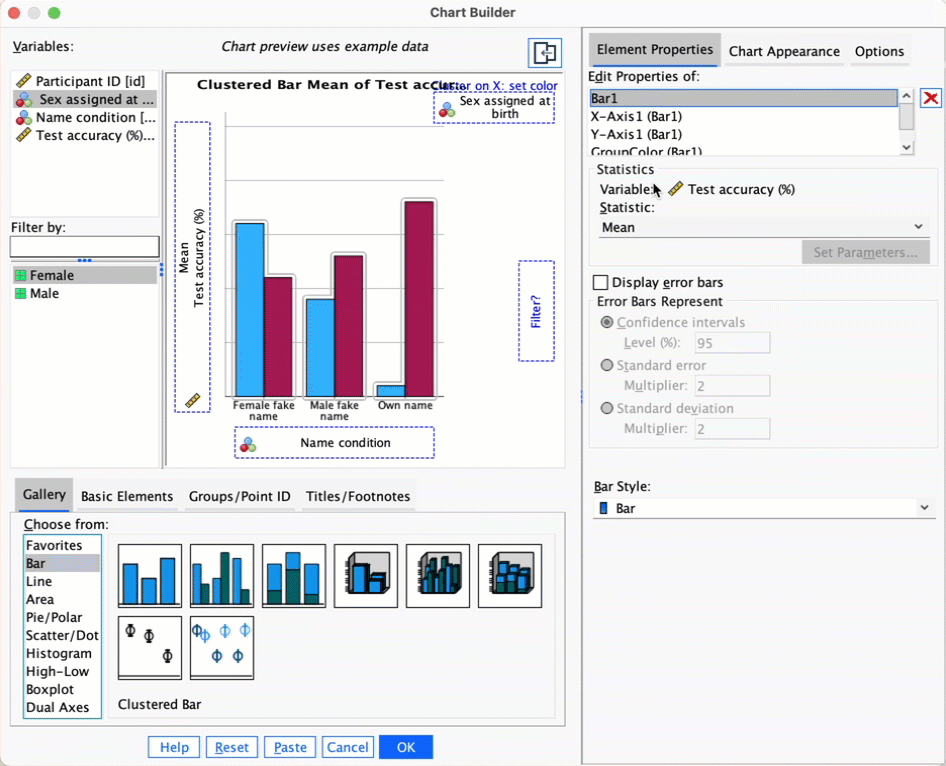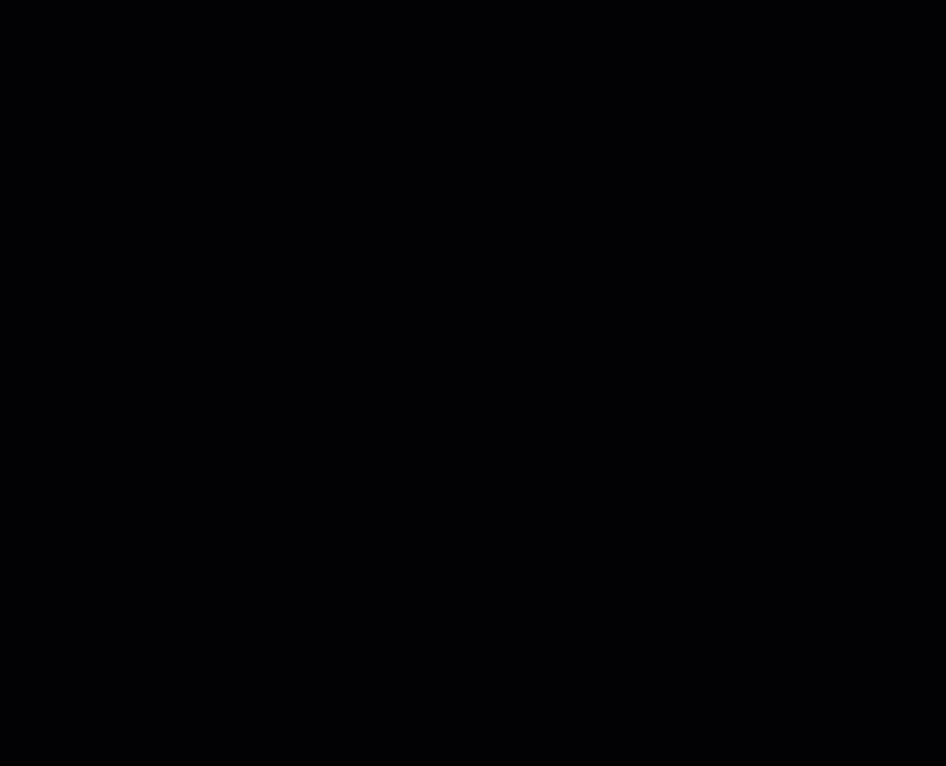
zang_sample.savdata from Chapter 4 (Task 8) plot a clustered error bar chart of the mean test accuracy as a function of the type of name participants completed the test under (x-axis) and whether they were male or female (different coloured bars).
To plot these data we need to select a clustered bar chart in the chart builder. First we need to drag accuracy into the  drop zone. Next we need to drag
drop zone. Next we need to drag name_type into the  drop zone. Finally, we drag
drop zone. Finally, we drag sex into the  drop zone. The two sexes will now be displayed as different-coloured bars. Add error bars by selecting
drop zone. The two sexes will now be displayed as different-coloured bars. Add error bars by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
The resulting plot looks like this:
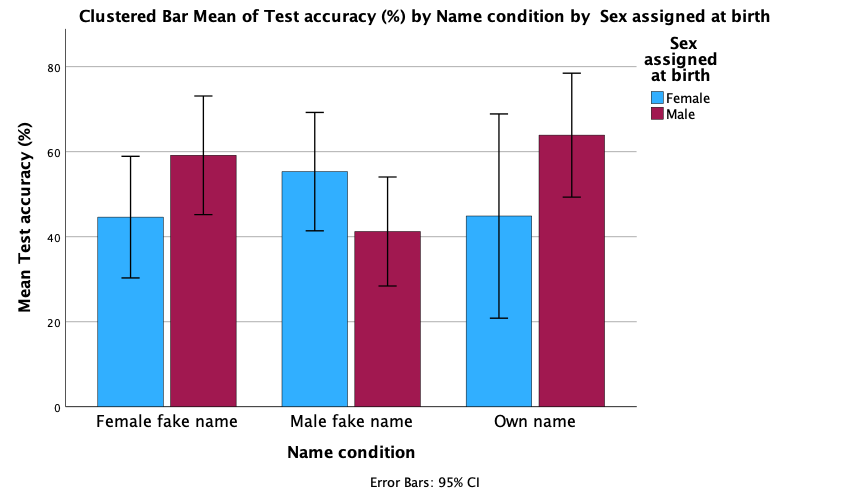
The plot shows that, on average, males did better on the test than females when using their own name (the control) but also when using a fake female name. However, for participants who did the test under a fake male name, the women did better than males.
Task 5.8
Using the
teach_method.savdata from Chapter 4 (Task 3), plot a clustered error line chart of the mean score when electric shocks were used compared to being nice, and plot males and females as different-coloured lines.
To plot these data we need to select a multiple line chart in the chart builder. In the variable list select the method variable and drag it into  . Then drag the variable
. Then drag the variable mark into  . Next, drag the variable
. Next, drag the variable sex into  . The two groups will now be displayed as different-coloured bars. Add error bars by selecting
. The two groups will now be displayed as different-coloured bars. Add error bars by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
The resulting plot looks like this:
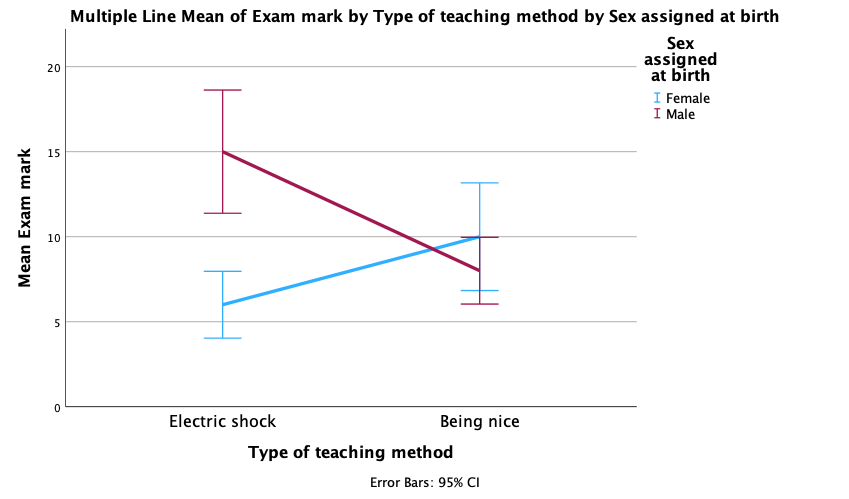
We can see that when the being nice method of teaching is used, males and females have comparable scores on their SPSS homework, with females scoring slightly higher than males on average, although their scores are also more variable than the males’ scores as indicated by the longer error bar). However, when an electric shock is used, males score higher than females but there is more variability in the males’ scores than the females’ for this method (as seen by the longer error bar for males than for females). Additionally, the plot shows that females score higher when the being nice method is used compared to when an electric shock is used, but the opposite is true for males. This suggests that there may be an interaction effect of sex.
Task 5.9
Using the
shopping.savdata from Chapter 4 (Task 5), create two error bar plots comparing men and women (x-axis): one for the distance walked, and the other of the time spent shopping.
Let’s first do the plot for distance walked. In the chart builder double-click on the icon for a simple bar chart, then drag the distance variable from the variable list into the  drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for males and females, drag the variable
drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for males and females, drag the variable sex from the variable list and into the drop zone for the x-axis ( ). Finally, add error bars to your bar chart by selecting
). Finally, add error bars to your bar chart by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
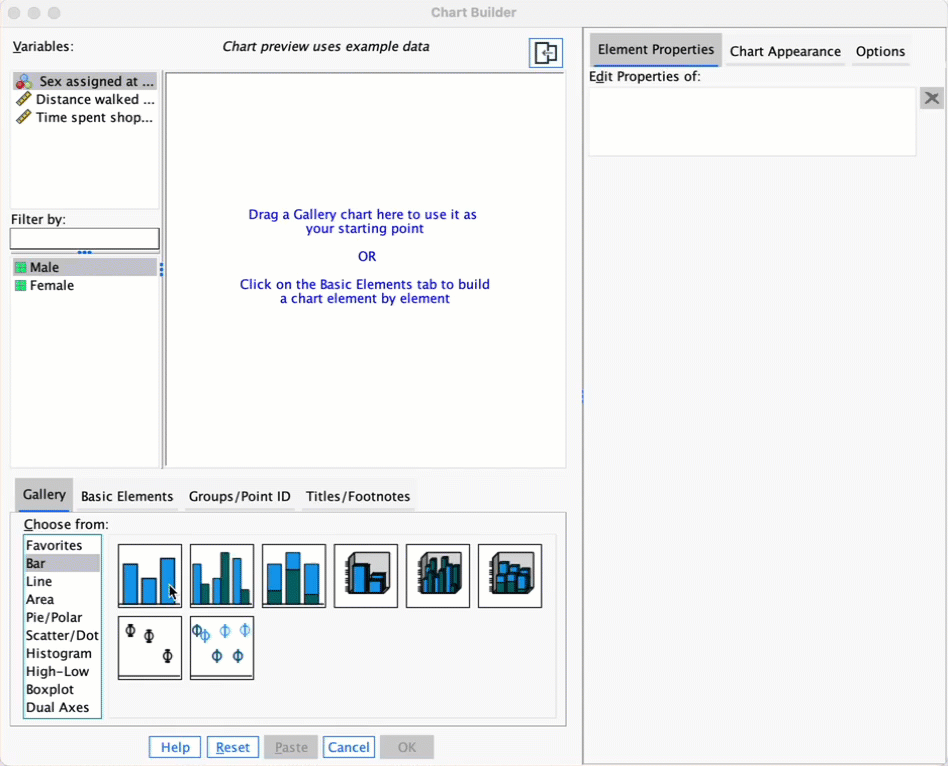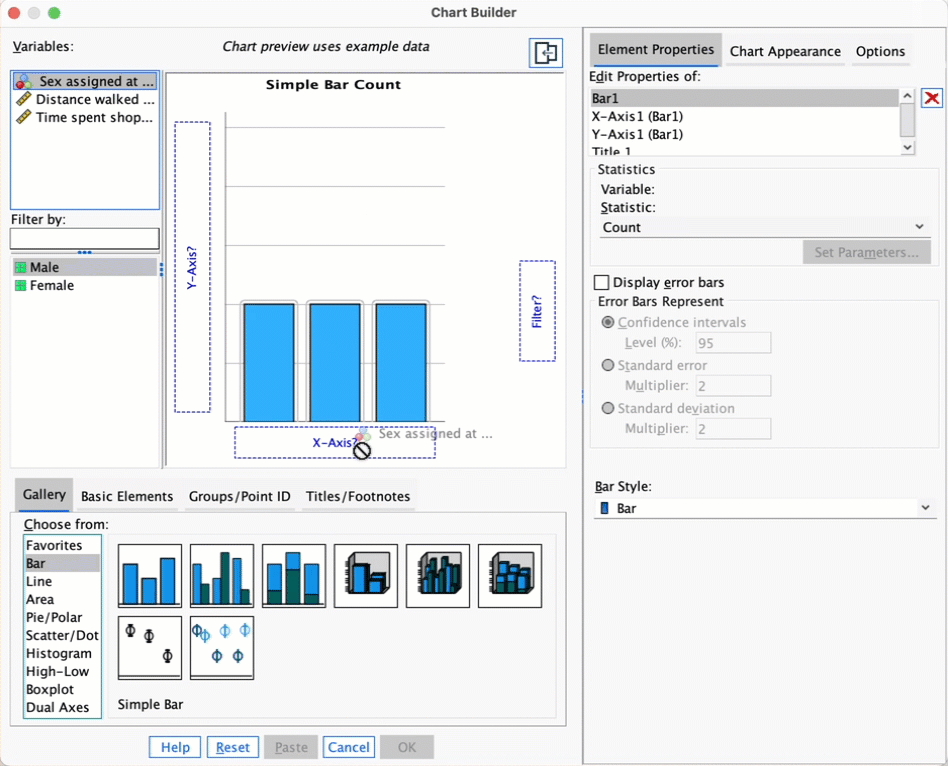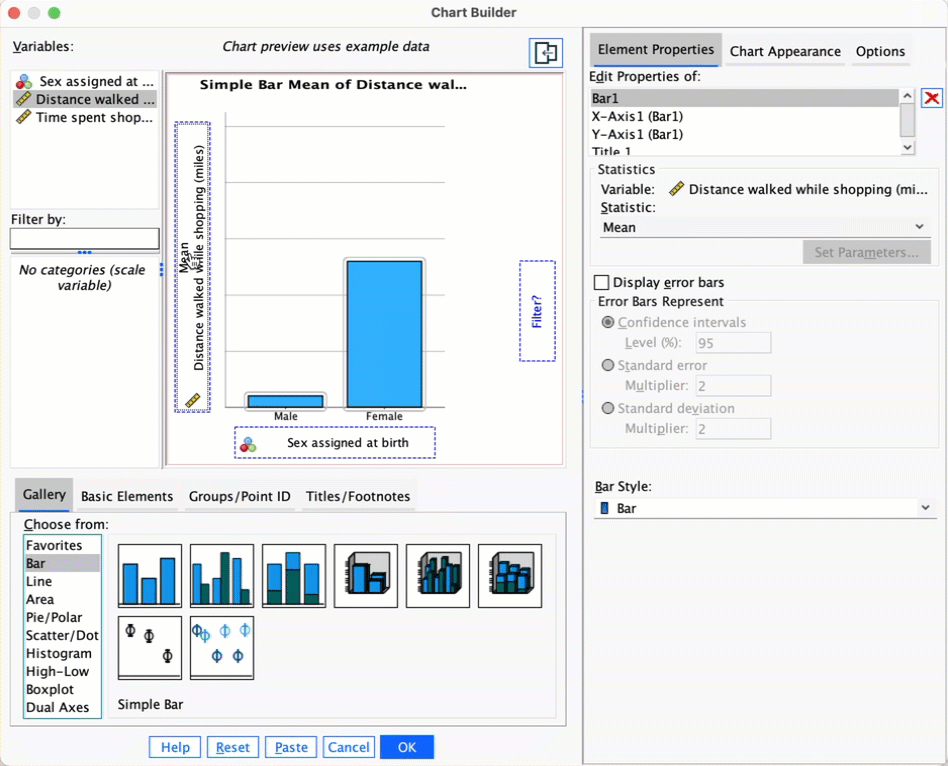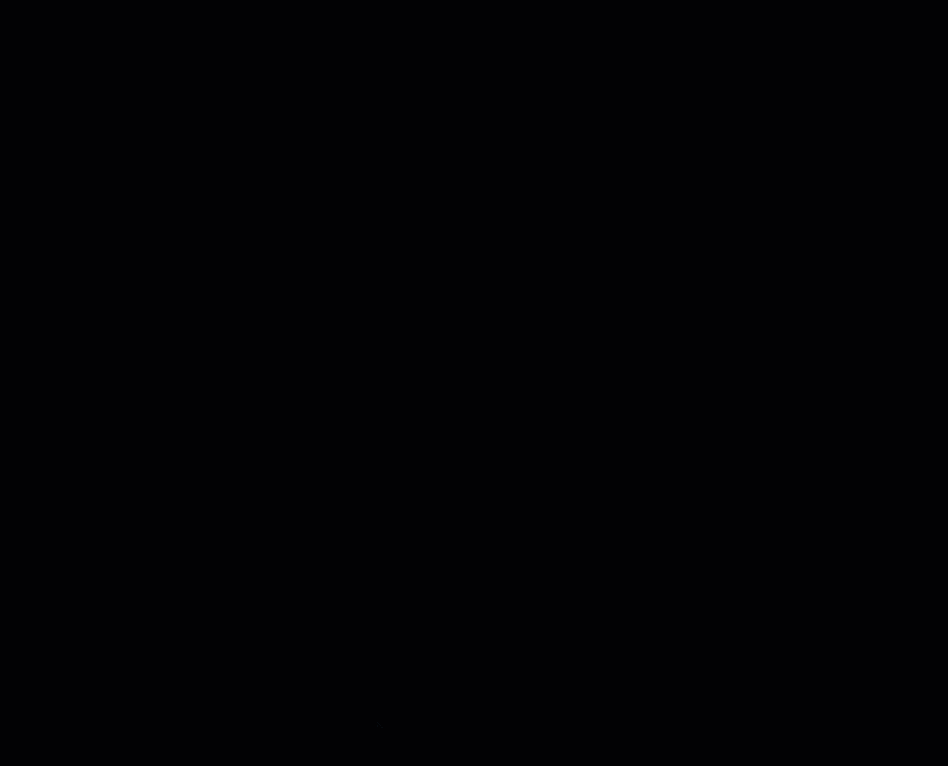
The resulting plot looks like this:
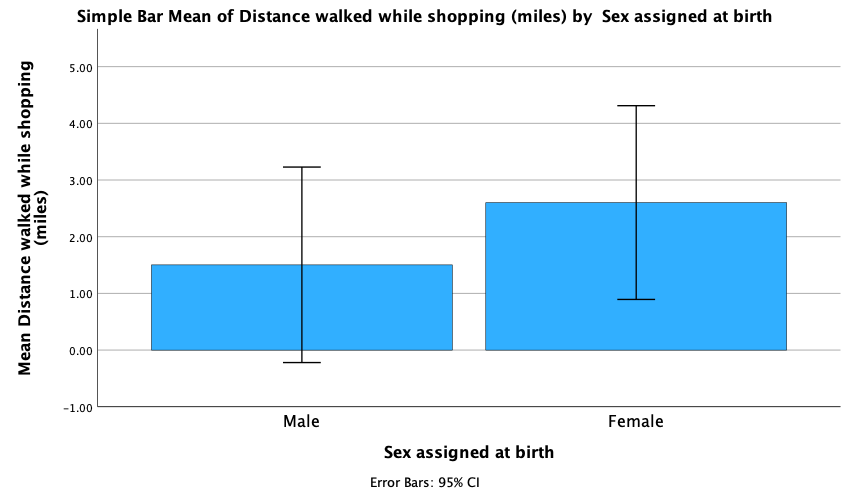
Looking at the plot above, we can see that, on average, females walk longer distances while shopping than males.
Next we need to do the plot for time spent shopping. In the chart builder double-click on the icon for a simple bar chart. Drag the time variable from the variable list into the  drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for males and females, drag the variable
drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for males and females, drag the variable sex from the variable list and into the drop zone for the x-axis ( ). Finally, add error bars to your bar chart by selecting
). Finally, add error bars to your bar chart by selecting  in the Element Properties dialog box. The finished chart builder will look like this:
in the Element Properties dialog box. The finished chart builder will look like this:
The resulting plot looks like this:
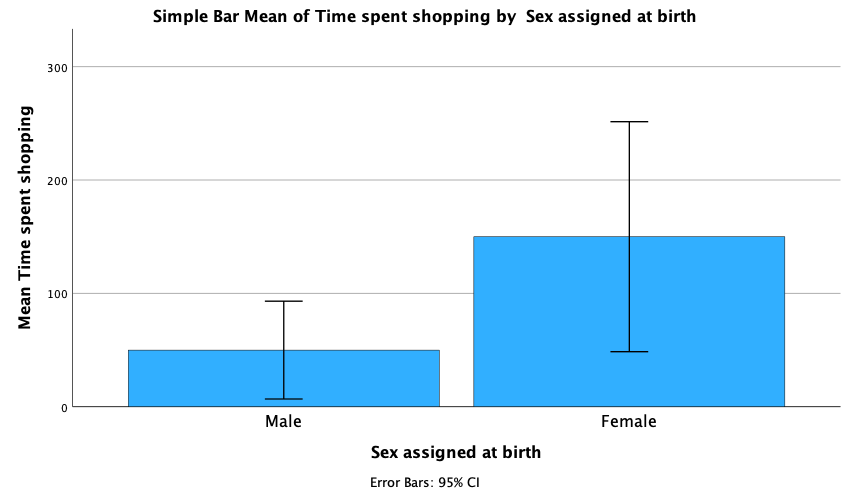
The plot shows that, on average, females spend more time shopping than males. The females’ scores are more variable than the males’ scores (longer error bar).
Task 5.10
Using the
pets.savdata from Chapter 4 (Task 6), plot two error bar charts comparing scores when having a fish or cat as a pet (x-axis): one for the animal liking variable, and the other for the life satisfaction.
Let’s first do the plot for the love of animals variable (animal). In the chart builder double-click on the icon for a simple bar chart, then drag the animal variable from the variable list into the  drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for different pets, drag the variable
drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for different pets, drag the variable pet from the variable list into the drop zone for the x-axis ( ). Finally, add error bars to your bar chart by selecting
). Finally, add error bars to your bar chart by selecting  in the Element Properties dialog box.
in the Element Properties dialog box.
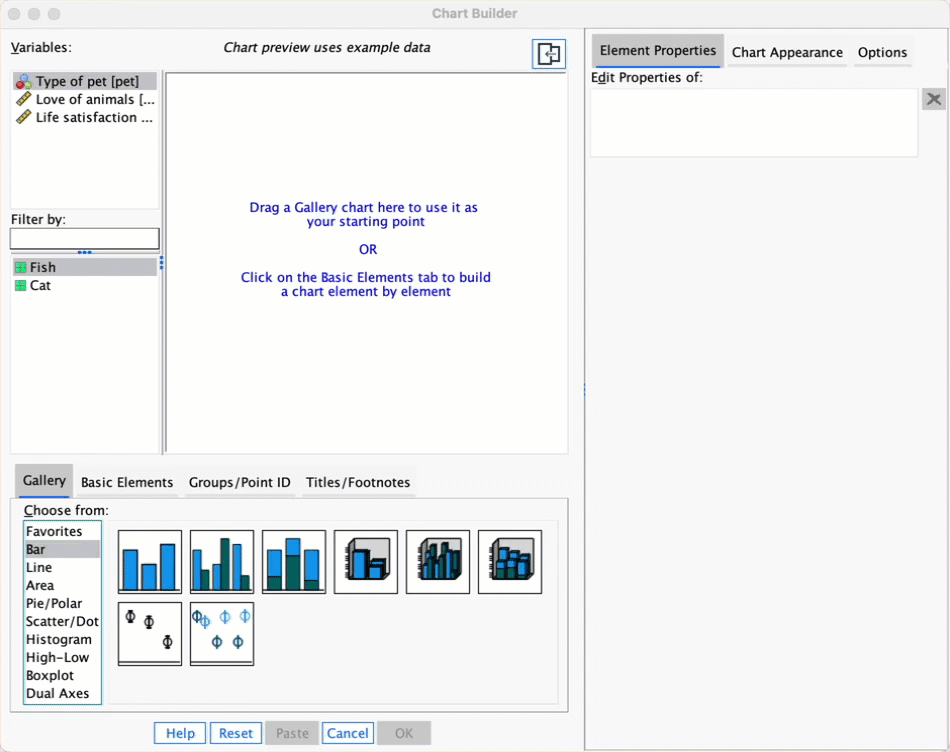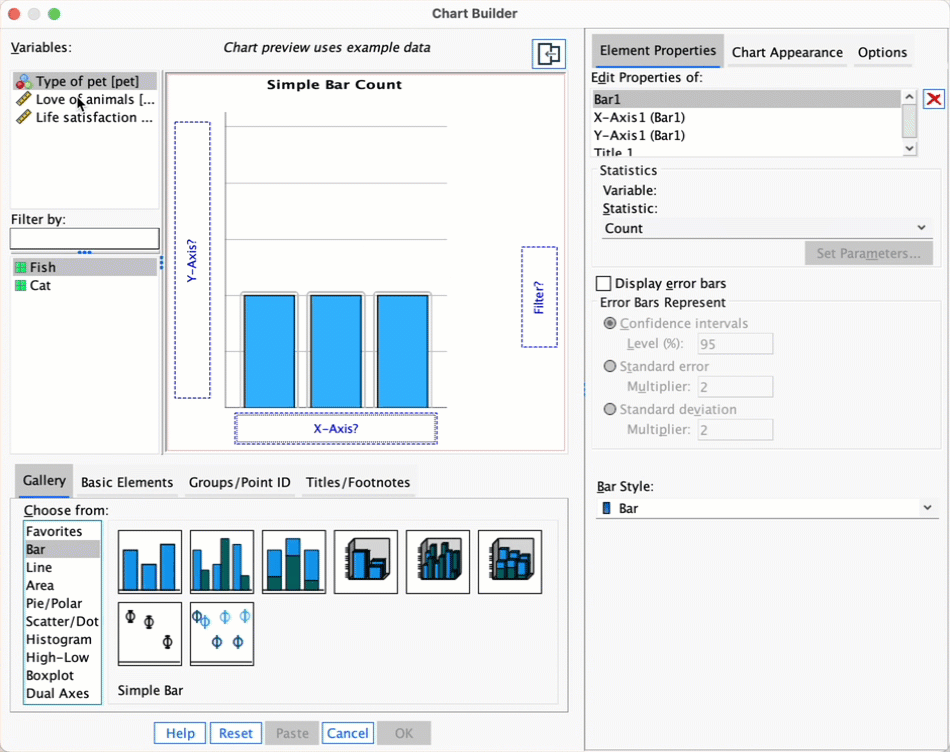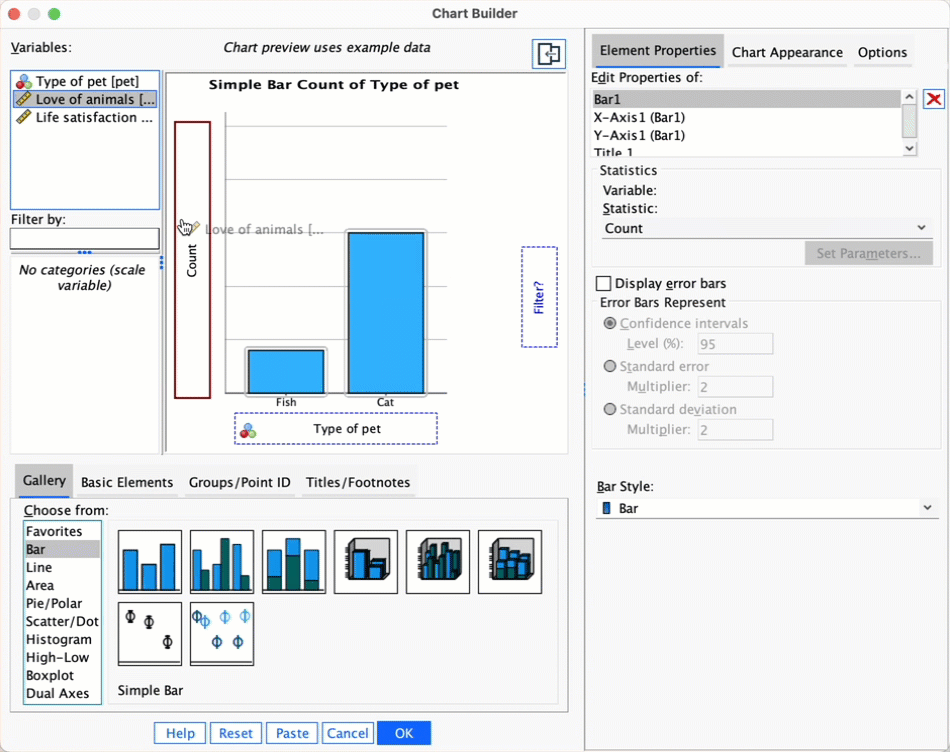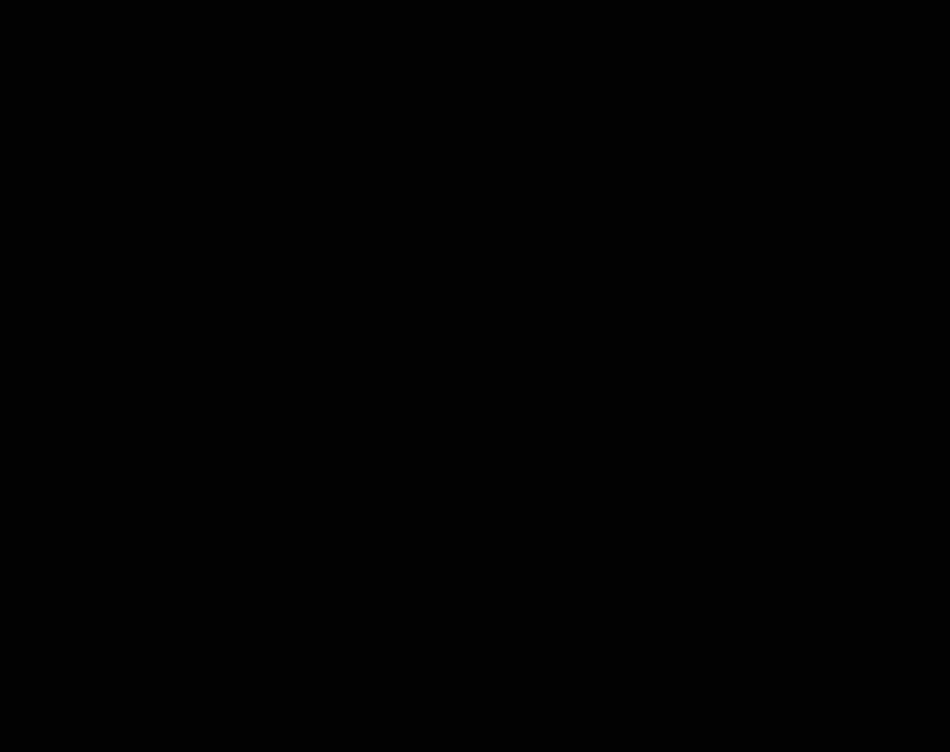
The resulting plot looks like this:
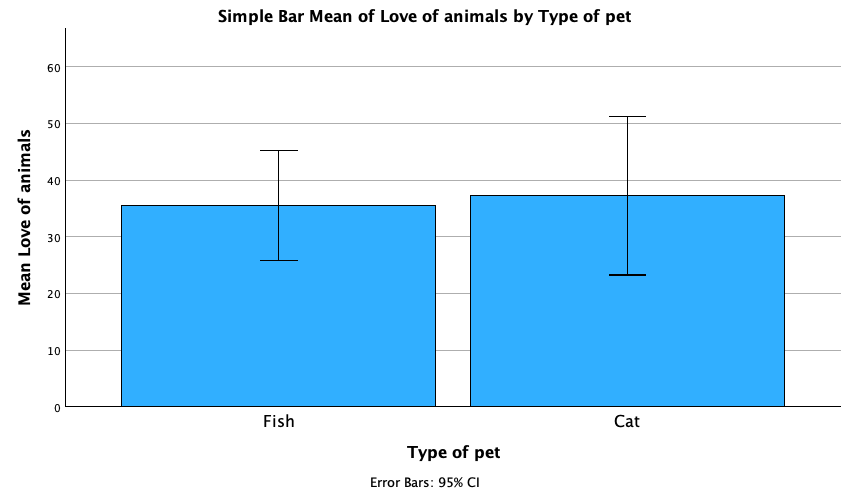
The plot shows that the mean love of animals was the same for people with cats and fish as pets.
Next we need to do the plot for life satisfaction. In the chart builder double-click on the icon for a simple bar chart. Drag the life_satisfaction variable from the variable list into the  drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for different pets, drag the variable
drop zone. The x-axis should be the variable by which we want to split the data. To plot the means for different pets, drag the variable pet from the variable list into the drop zone for the x-axis ( ). Finally, add error bars to your bar chart by selecting
). Finally, add error bars to your bar chart by selecting  in the Element Properties dialog box.
in the Element Properties dialog box.
The resulting plot looks like this:
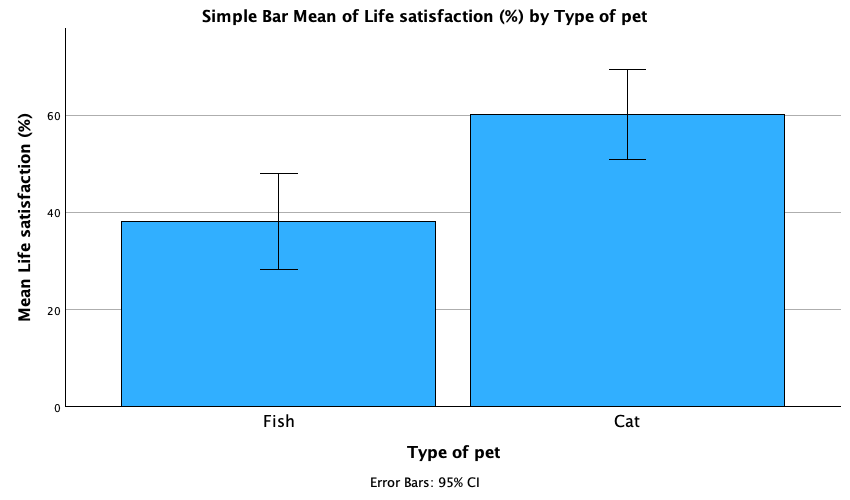
The plot shows that, on average, life satisfaction was higher in people who had cats for pets than for those with fish.
Task 5.11
Using the same data as above, plot a scatterplot of animal liking scores against life satisfaction (plot scores for those with fishes and cats in different colours).
Access the chart builder and select a grouped scatterplot. It doesn’t matter which way around we plot these variables, so let’s drag life_satisfaction from the variable list into the  drop zone and then drag
drop zone and then drag animal from the variable list into the drop zone for the x-axis ( ). We then need to split the scatterplot by cats and fish, so drag
). We then need to split the scatterplot by cats and fish, so drag pet to the  drop zone.
drop zone.
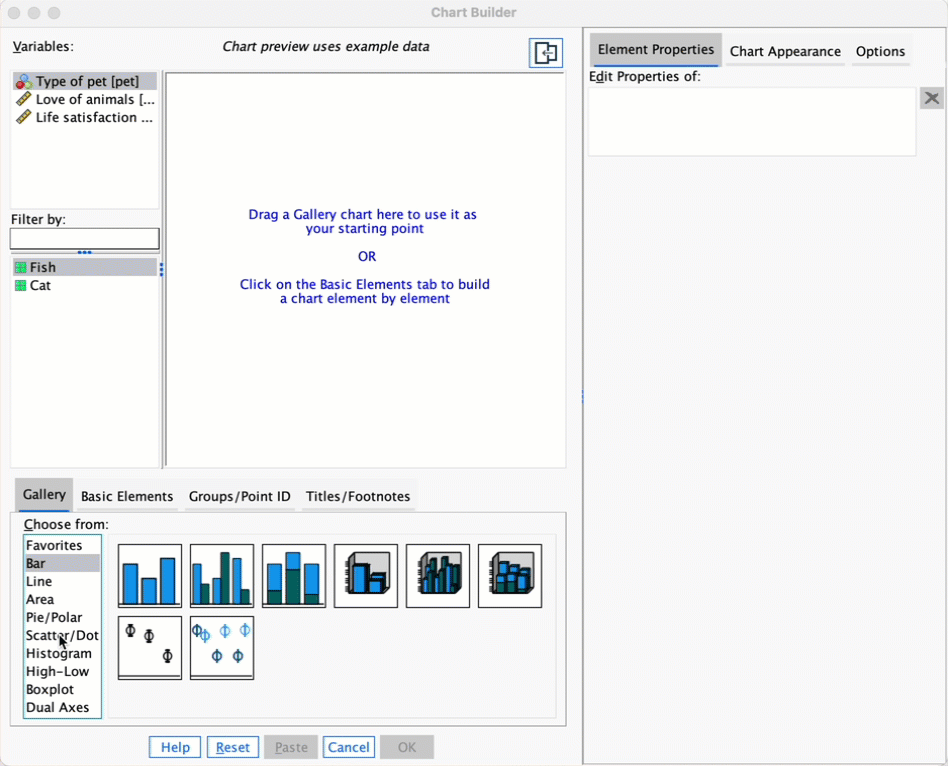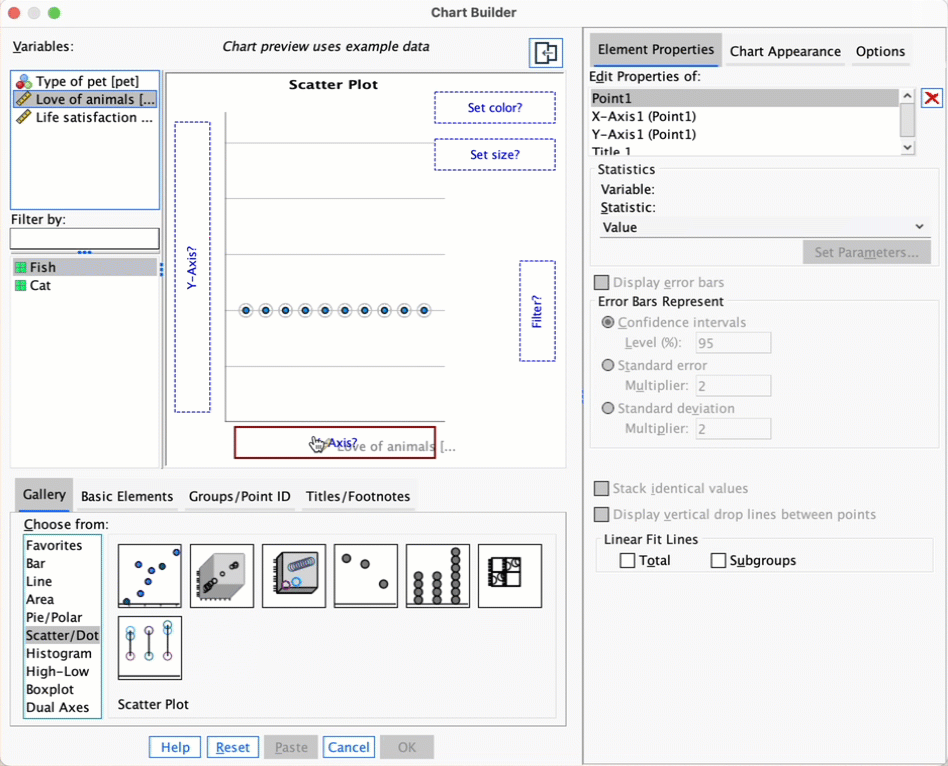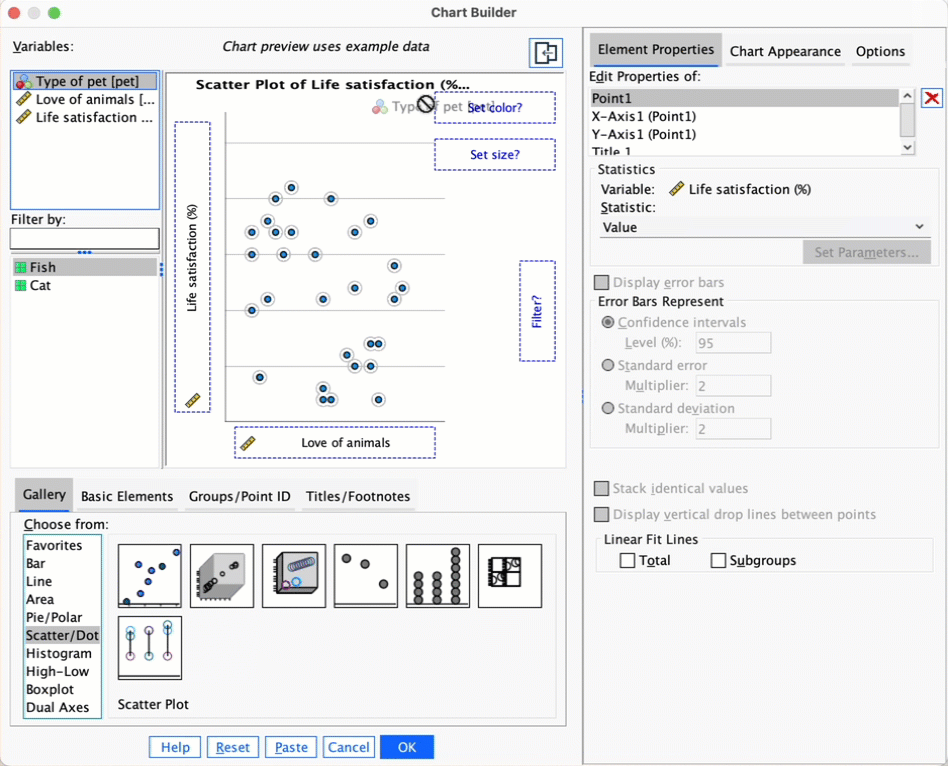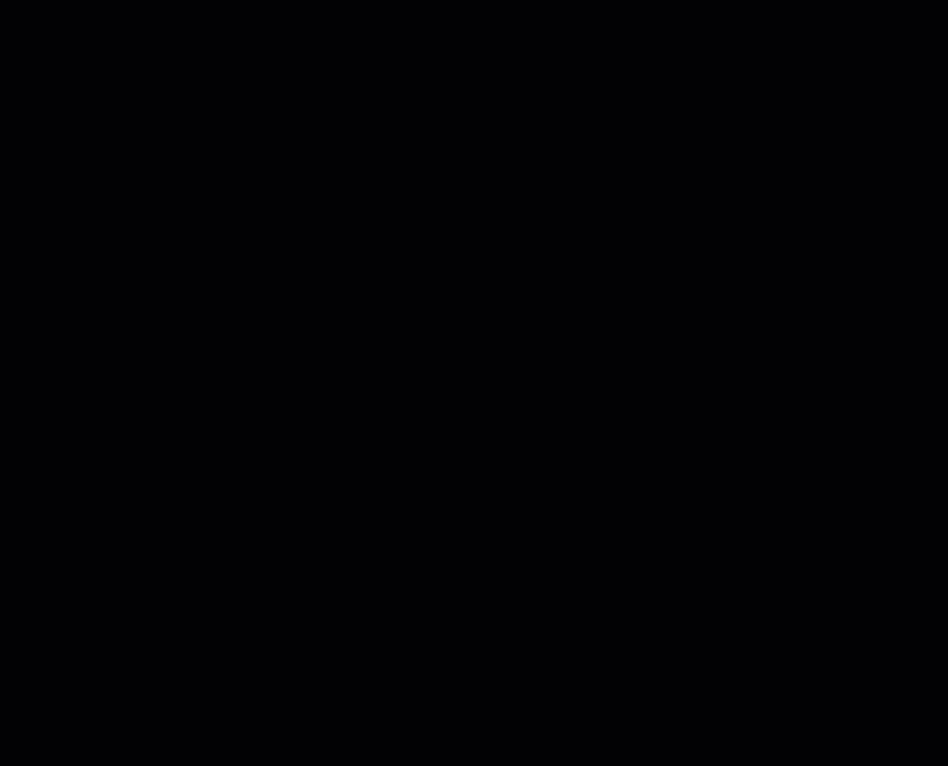
Click on  to produce the plot. Let’s fit some regression lines to make the plot easier to interpret. To do this, double-click on the plot in the SPSS viewer to open it in the SPSS chart editor. Then click on
to produce the plot. Let’s fit some regression lines to make the plot easier to interpret. To do this, double-click on the plot in the SPSS viewer to open it in the SPSS chart editor. Then click on ![]() in the chart editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on
in the chart editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on  to fit the lines:
to fit the lines:
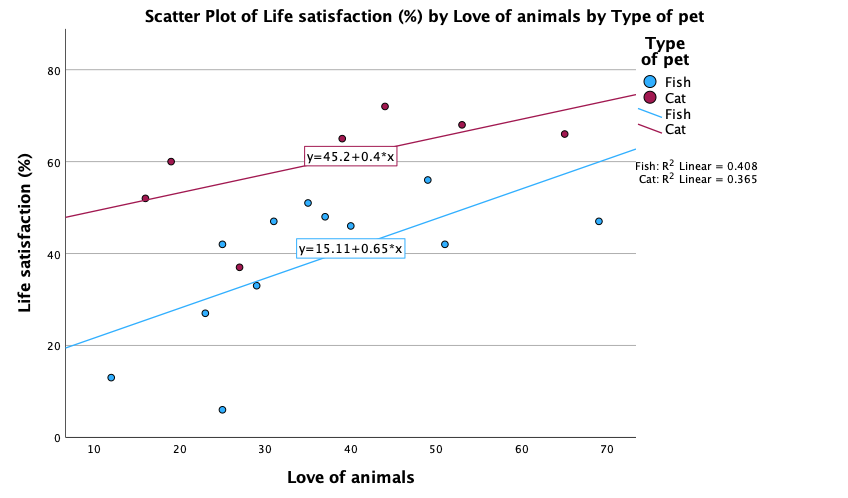
We can conclude that for men married to both goats and dogs, as love of animals increases so does life satisfaction (a positive relationship). However, this relationship is more pronounced for goats than for dogs (steeper regression line for goats than for dogs).
Task 5.12
Using the
tea_15.savdata from Chapter 4 (Task 7), plot a scatterplot showing the number of cups of tea drunk (x-axis) against cognitive functioning (y-axis).
In the chart builder double-click on the icon for a simple scatterplot. Select the cognitive functioning variable from the variable list and drag it into the  drop zone. The horizontal axis should display the independent variable (the variable that predicts the outcome variable). In this case is it is the number of cups of tea drunk, so click on this variable in the variable list and drag it into the drop zone for the x-axis (
drop zone. The horizontal axis should display the independent variable (the variable that predicts the outcome variable). In this case is it is the number of cups of tea drunk, so click on this variable in the variable list and drag it into the drop zone for the x-axis ( ). The completed dialog box will look like this:
). The completed dialog box will look like this:
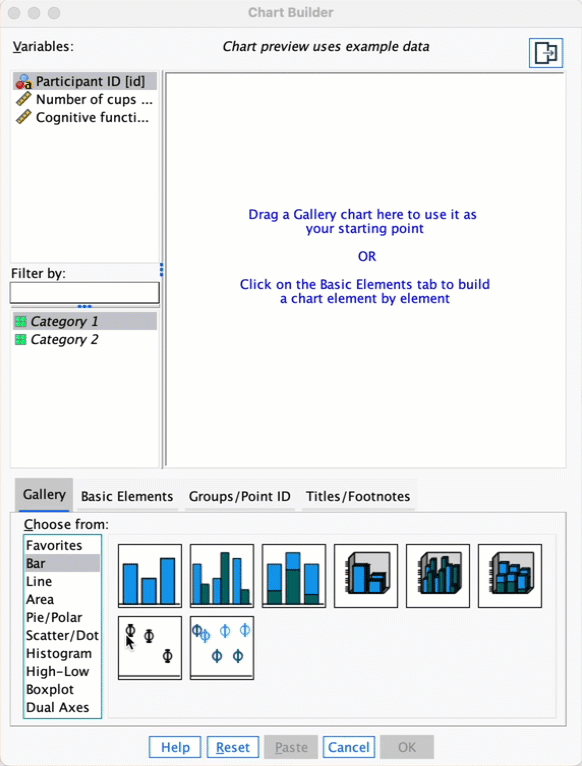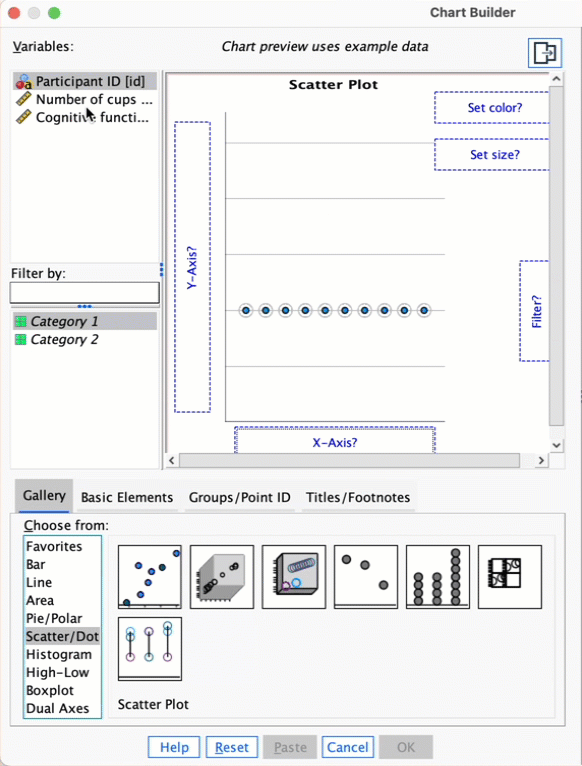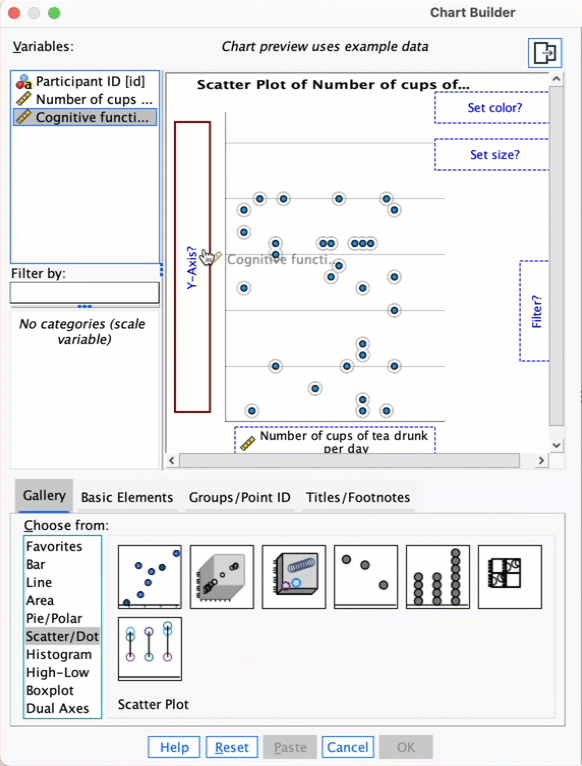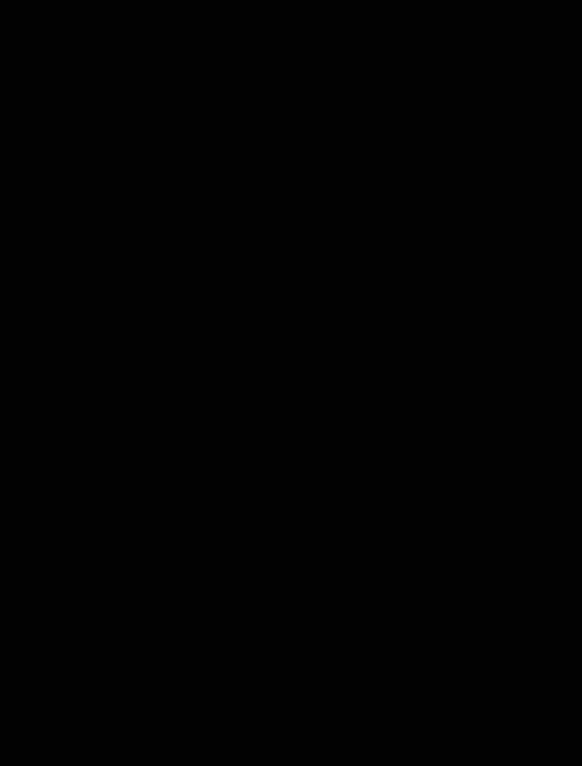
Click on  to produce the plot. Let’s fit a regression line to make the plot easier to interpret. To do this, double-click on the plot in the SPSS Viewer to open it in the SPSS Chart Editor. Then click on in the Chart Editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on
to produce the plot. Let’s fit a regression line to make the plot easier to interpret. To do this, double-click on the plot in the SPSS Viewer to open it in the SPSS Chart Editor. Then click on in the Chart Editor to open the properties dialog box. In this dialog box, ask for a linear model to be fitted to the data (this should be set by default). Click on ![]() to fit the line. The resulting plot should look like this:
to fit the line. The resulting plot should look like this:
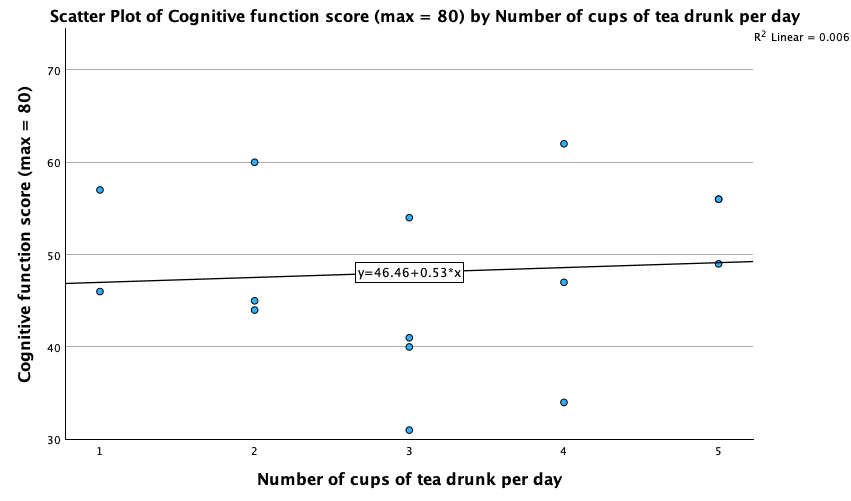
The scatterplot (and near-flat line especially) tells us that there is a tiny relationship (practically zero) between the number of cups of tea drunk per day and cognitive function.
Chapter 6
Task 6.1
Using the
notebook.savdata, check the assumptions of normality and homogeneity of variance for the two films (ignoresex). Are the assumptions met?
We can get descriptive information about our variables by following the general procedure. The resulting output is in Figure 42 to Figure 44.
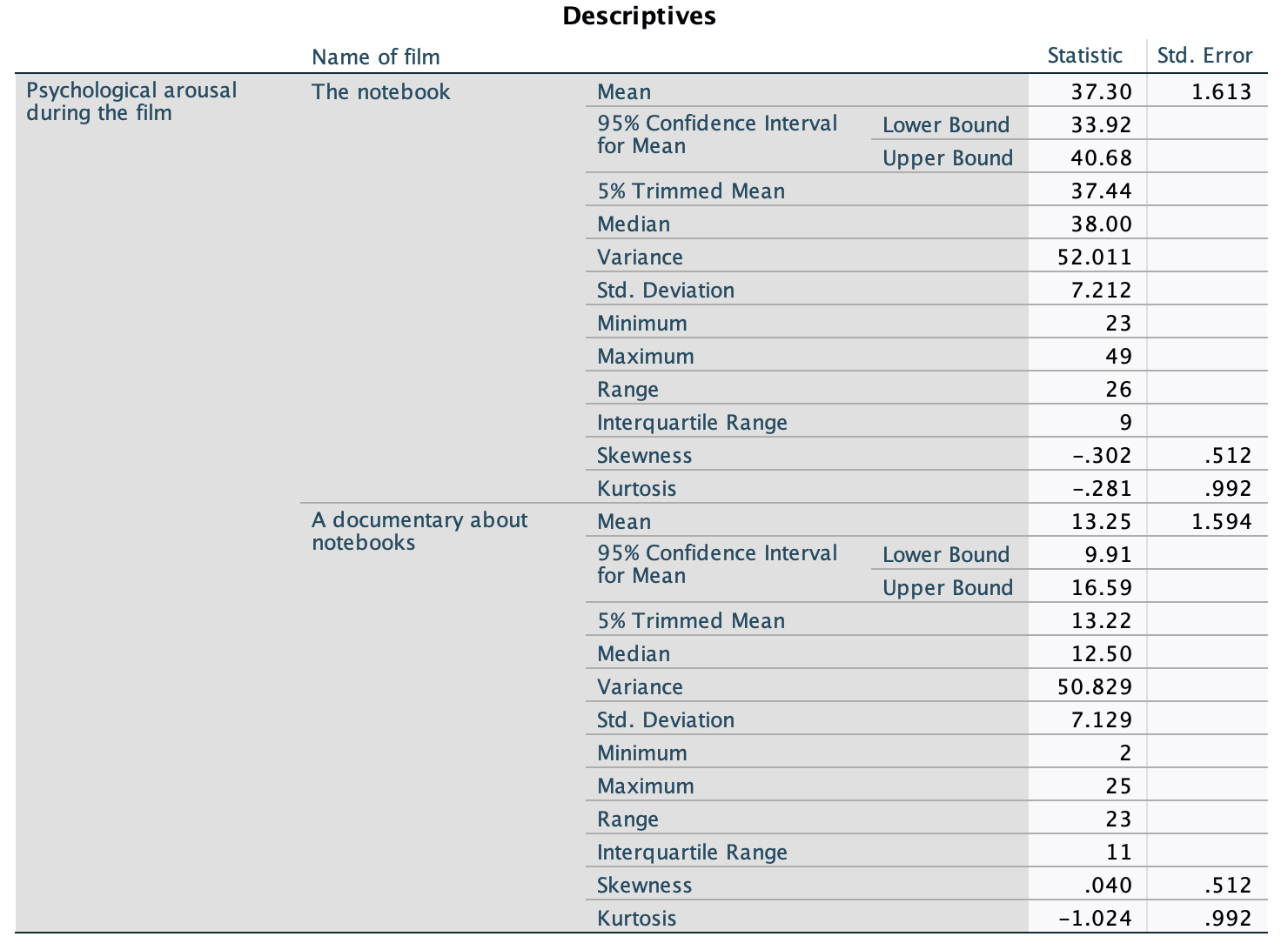
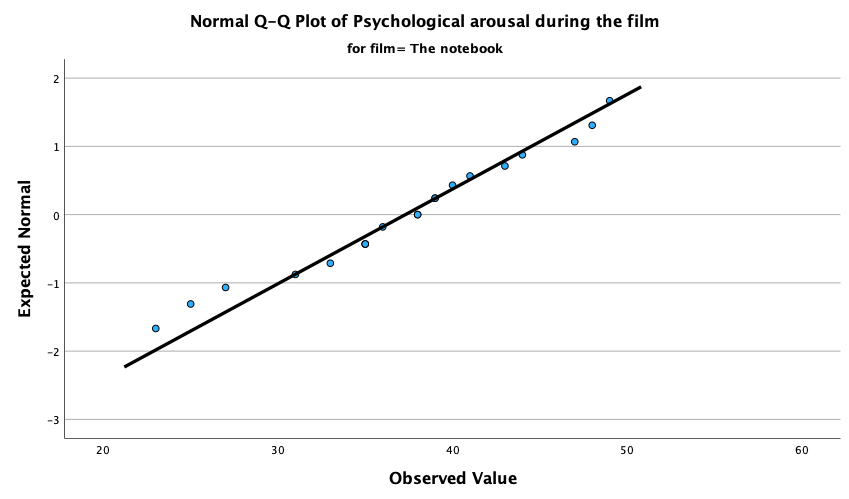
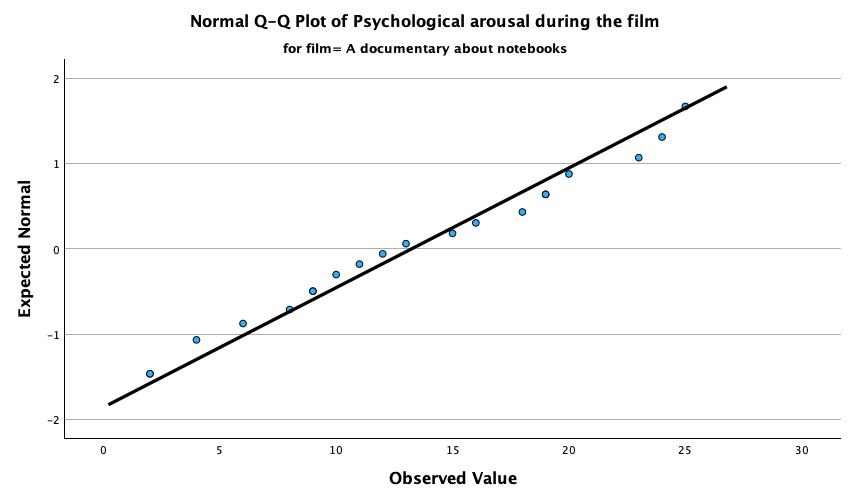
The Q-Q plots suggest that for both films the expected quantile points are close to those that would be expected from a normal distribution (i.e. the dots fall close to the diagonal line). The descriptive statistics confirm this conclusion. The skewness statistics gives rise to a z-score of \(z_\text{skew} = \frac{−0.320}{0.512} = –0.63\) for The Notebook, and \(z_\text{skew} = \frac{0.04}{0.512} = 0.08\) for a documentary about notebooks. These show no excessive (or significant) skewness. For kurtosis these values are \(z_\text{kurtosis} = \frac{−0.281}{0.992} = –0.28\) for The Notebook, and \(z_\text{kurtosis} = \frac{–1.024}{0.992} = –1.03\) for a documentary about notebooks. None of these z-scores are large enough to concern us. More important the raw values of skew and kurtosis are close enough to zero.
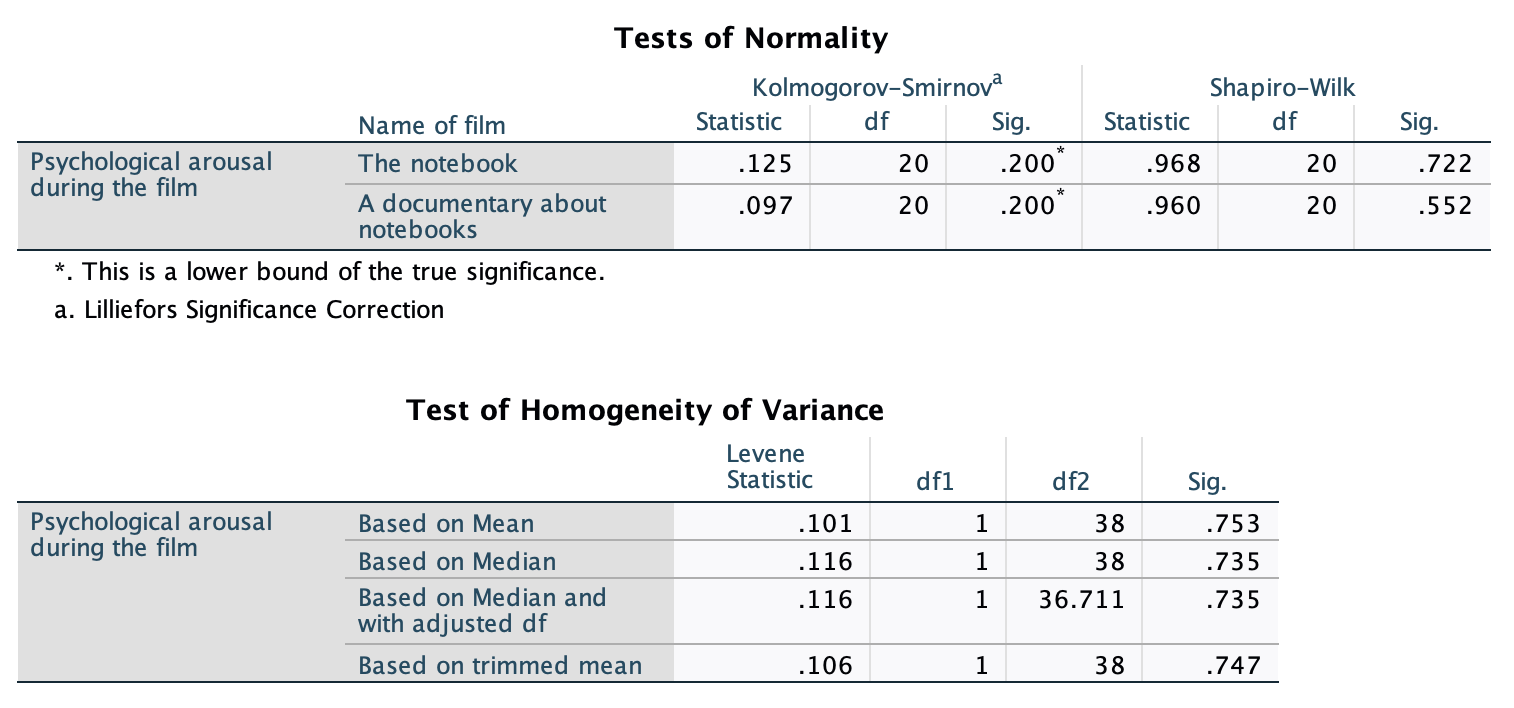
In the Chapter we talk a lot about NOT using significance tests of assumptions, so proceed with caution here. The K-S tests show no significant deviation from normality for both films. Arousal scores for The Notebook, D(20) = 0.13, p = 0.20, and a documentary about notebooks, D(20) = 0.10, p = 0.20, were both not significantly different from a normal distribution. If you chose to ignore my advice and use these sorts of tests then you might assume normality. However, the sample is small and these tests would have been very underpowered to detect a deviation from normal.
In terms of homogeneity of variance, again Levene’s test will be underpowered, and I prefer to ignore this test altogether, but if you’re the sort of person who doesn’t ignore it, it shows that the variances of arousal for the two films were not significantly different, F(1, 38) = 0.10, p = 0.753.
Task 6.2
The file
spss_exam.savcontains data on students’ performance on an SPSS exam. Four variables were measured:exam(first-year SPSS exam scores as a percentage),computer(measure of computer literacy as a percentage),lecture(percentage of SPSS lectures attended) andnumeracy(a measure of numerical ability out of 15). There is a variable calleduniindicating whether the student attended Sussex University (where I work) or Duncetown University. Compute and interpret descriptive statistics forexam,computer,lectureandnumeracyfor the sample as a whole.
We can again use the Explore command. Follow the general procedure and place all four variables (exam, computer, lecture and numeracy) in the Dependent List section of the main dialog box (Figure 46)
The output shows the table of descriptive statistics for the four variables in this example. We can put the different variable sin columns (rather than rows) by double clicking and pivoting the rows to columns:
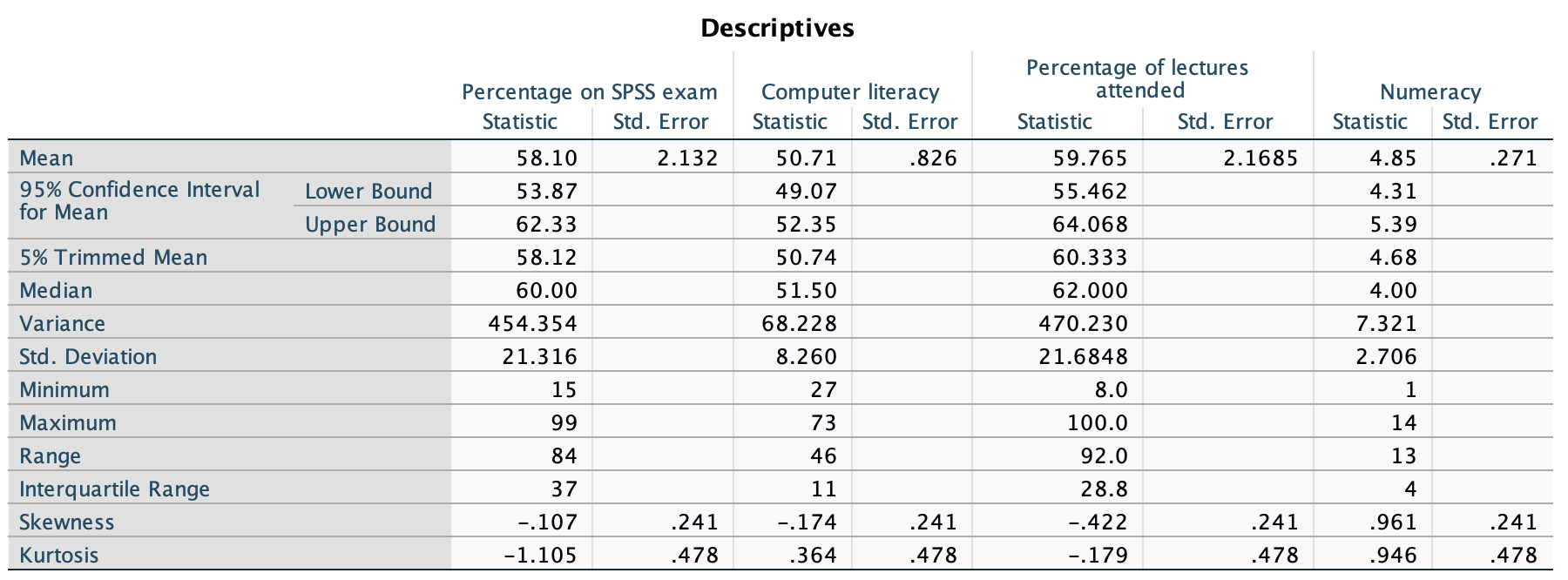
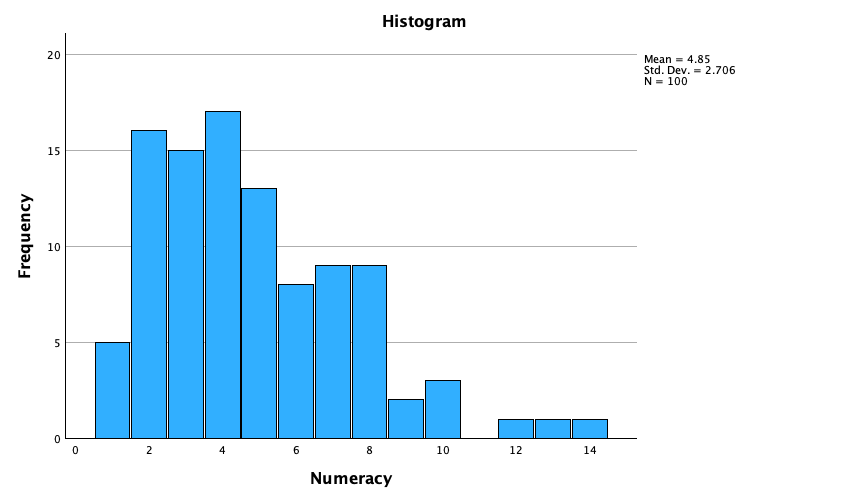
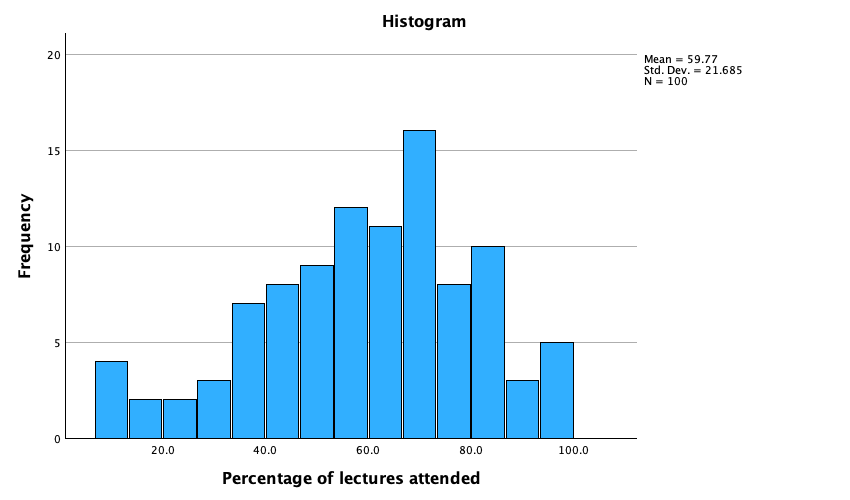
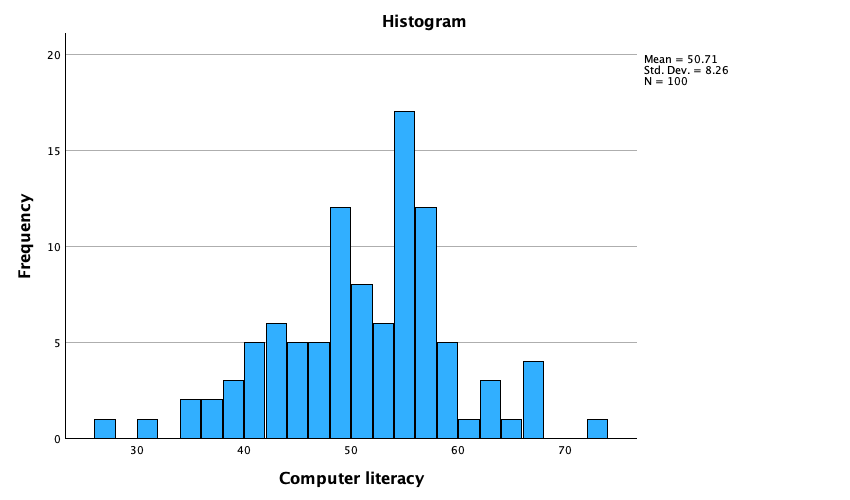
From this table (Figure 48), we can see that, on average, students attended nearly 60% of lectures, obtained 58% in their SPSS exam, scored only 51% on the computer literacy test, and only 5 out of 15 on the numeracy test. In addition, the standard deviation for computer literacy was relatively small compared to that of the percentage of lectures attended and exam scores. The range of scores on the exam was wide (15-99%) as was lecture attendence (8-100%).
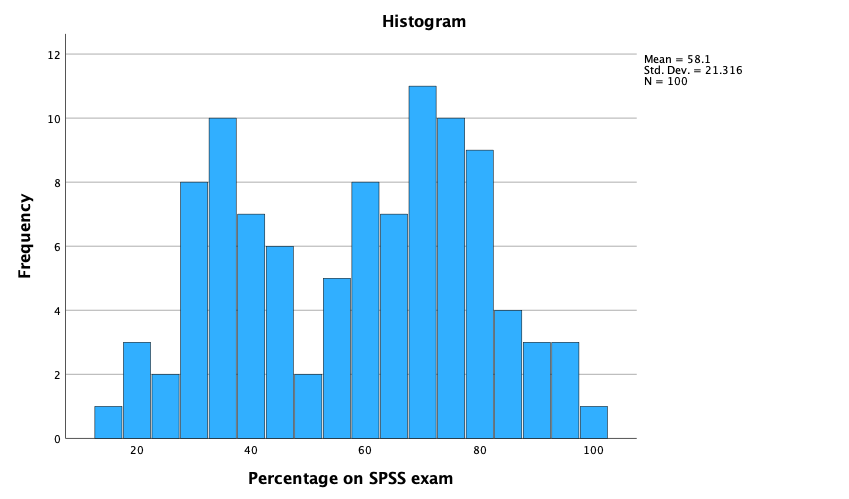
Descriptive statistics and histograms are a good way of getting an instant picture of the distribution of your data. This snapshot can be very useful:
- The exam scores (Figure 49) look suspiciously bimodal (there are two peaks, indicative of two modes). The bimodal distribution of SPSS exam scores alerts us to a trend that students are typically either very good at statistics or struggle with it (there are relatively few who fall in between these extremes). Intuitively, this finding fits with the nature of the subject: once everything falls into place it’s possible to do very well on statistics modules, but before that enlightenment occurs it all seems hopelessly difficult!
- The numeracy test (Figure 50) has produced very positively skewed data (the majority of people did very badly on this test and only a few did well). This corresponds to what the skewness statistic indicated.
- Lecture attendance (Figure 51) looks relatively normally distributed. There is a slight negative skew suggesting that although most students attend at least 40% of lectures there is a small tail of students whop attend very few lectures. These students might have disengaged from the module and perhaps need some help to get back on track.
- Computer literacy (Figure 52) is fairly normally distributed. A few people are very good with computers and a few are very bad, but the majority of people have a similar degree of knowledge).
Task 6.3
Calculate and interpret the z-scores for skewness for all variables.
\[ \begin{aligned} z_{\text{skew, spss}} &= \frac{−0.107}{0.241} = −0.44 \\ z_{\text{skew, numeracy}} &= \frac{0.961}{0.241} = 3.99 \\ z_{\text{skew, computer literacy}} &= \frac{-0.174}{0.241} = −0.72 \\ z_{\text{skew, attendance}} &= \frac{−0.422}{0.241} = −1.75 \\ \end{aligned} \]
It is pretty clear that the numeracy scores are quite positively skewed (as we saw in Figure 50) because they have a z-score that is unusually high (nearly 4 standard deviations above the expected value of 0). This skew indicates a pile-up of scores on the left of the distribution (so most students got low scores). For the other three variables, the z-scores fall within reasonable limits although (as we saw in Figure 50 attendance is quite negatively skewed suggesting sok estudents have disengaged from their statistics module.)
Task 6.4
Calculate and interpret the z-scores for kurtosis for all variables.
\[ \begin{aligned} z_{\text{kurtosis, spss}} &= \frac{−1.105}{0.478} = −2.31 \\ z_{\text{kurtosis, numeracy}} &= \frac{0.946}{0.478} = 1.98 \\ z_{\text{kurtosis, computer literacy}} &= \frac{0.364}{0.478} = 0.76 \\ z_{\text{kurtosis, attendance}} &= \frac{-0.179}{0.478} = −0.37 \\ \end{aligned} \]
- The SPSS scores have negative excess kurtosis and the distribution is so-called platykurtic. In practical terms this means that there are fewer extreme scores than expected in the the distribution (the tails of the distribution are said to be thin/light because there are fewer scores than expected in them).
- The numeracy scores have positive excess kurtosis and the distribution is so-called leptokurtic. In practical terms this means that there are more extreme scores than expected in the the distribution (the tails of the distribution are said to be fat/heavy because there are more scores than expected in them).
- For computer literacy and attendance scores, the levels of excess kurtosis are within reasonable boundaries of what we might expect. In a broad sense we can assume these distributions are approximately mesokurtic.
Task 6.5
Use the split file command to look at and interpret the descriptive statistics for
numeracyandexam.
If we want to obtain separate descriptive statistics for each of the universities, we can split the file, and then proceed using the Explore command. Select ![]() to access the Split File dialog box. Select the option Organize output by groups and drag
to access the Split File dialog box. Select the option Organize output by groups and drag Uni into the box labelled Groups Based on (Figure 53). Click  .
.
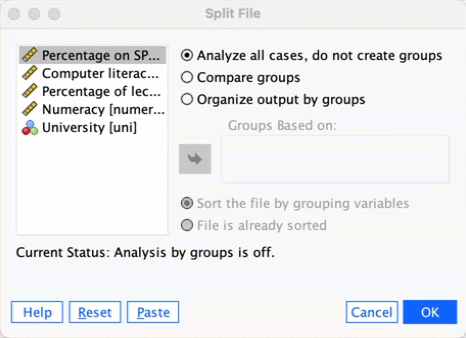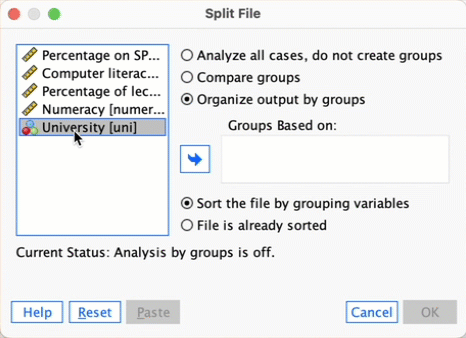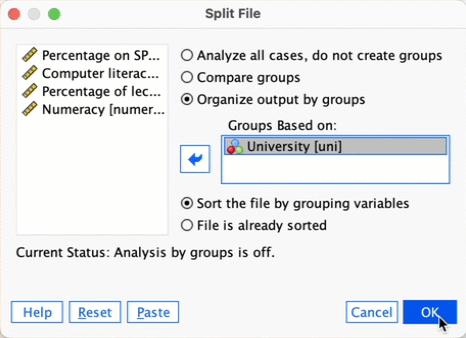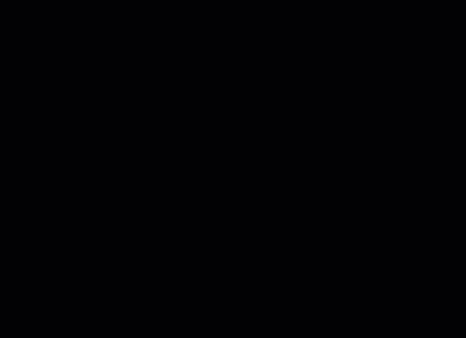
Once you have split the file, Follow the general procedure but drag exam and numeracy to the box labelled Dependent List.
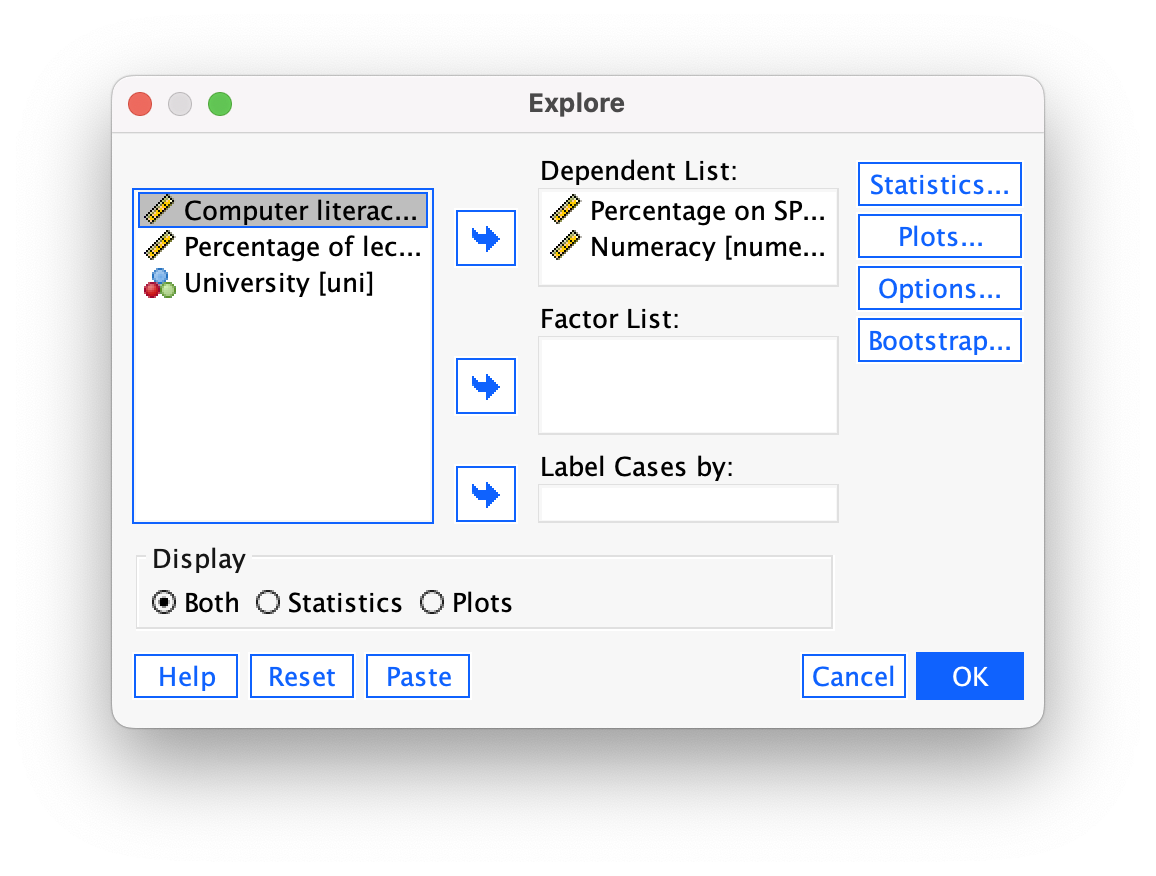
The output is split into two sections: first the results for students at Duncetown University (Figure 55), then the results for those attending Sussex University (Figure 56). From these tables it is clear that Sussex students scored higher on both their SPSS exam and the numeracy test than their Duncetown counterparts.Looking at the means, on average Sussex students scored an amazing 36% more on the SPSS exam than Duncetown students, and had higher numeracy scores too (what can I say, my students are the best).

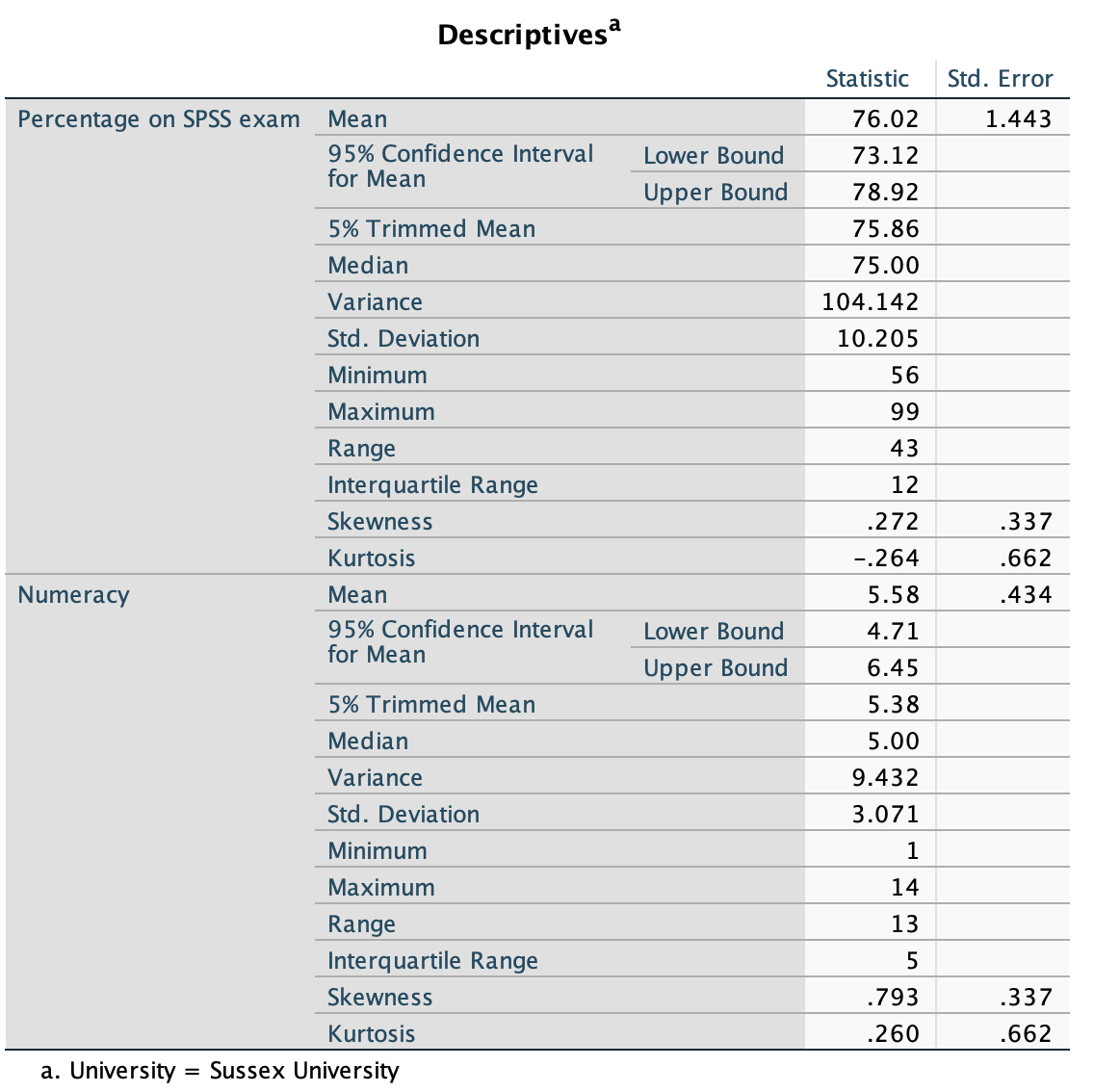
The histograms of these variables split according to the university attended show numerous things. The first interesting thing to note is that for exam marks, the distributions are both fairly normal (Figure 57 and Figure 58). This seems odd because the overall distribution was bimodal. However, it starts to make sense when you consider that for Duncetown the distribution is centred around a mark of about 40%, but for Sussex the distribution is centred around a mark of about 76%. This illustrates how important it is to look at distributions within groups. If we were interested in comparing Duncetown to Sussex it wouldn’t matter that overall the distribution of scores was bimodal; all that’s important is that residuals within each group are from a normal distribution, and in this case it appears to be true. When the two samples are combined, these two normal distributions create a bimodal one (one of the modes being around the centre of the Duncetown distribution, and the other being around the centre of the Sussex data).
For numeracy scores, the distribution is slightly positively skewed (there is a larger concentration at the lower end of scores) in both the Duncetown and Sussex groups (Figure 59 and Figure 60). Therefore, the overall positive skew observed before is due to the mixture of universities.
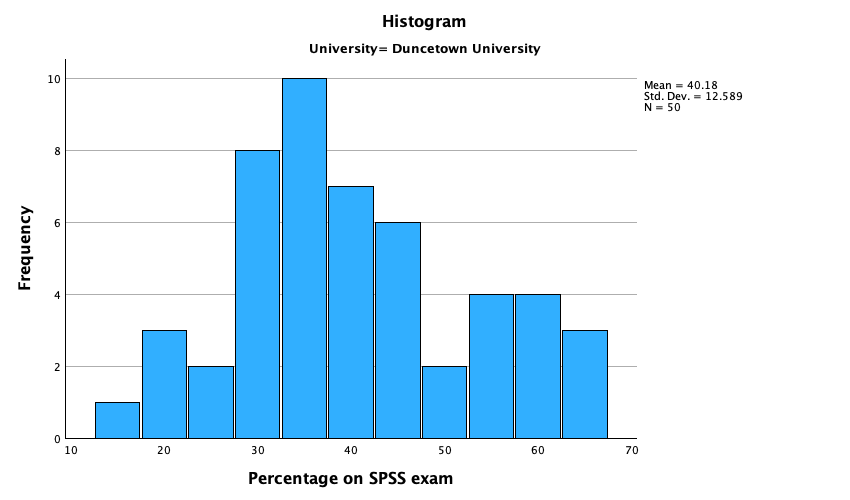
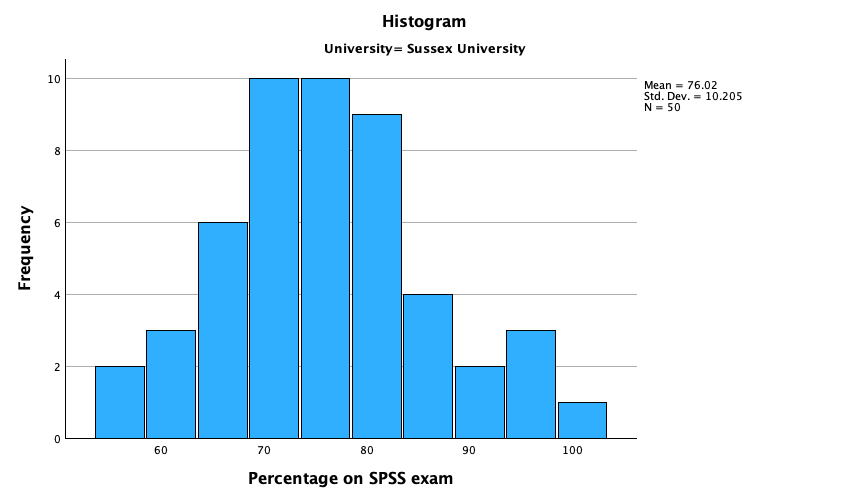
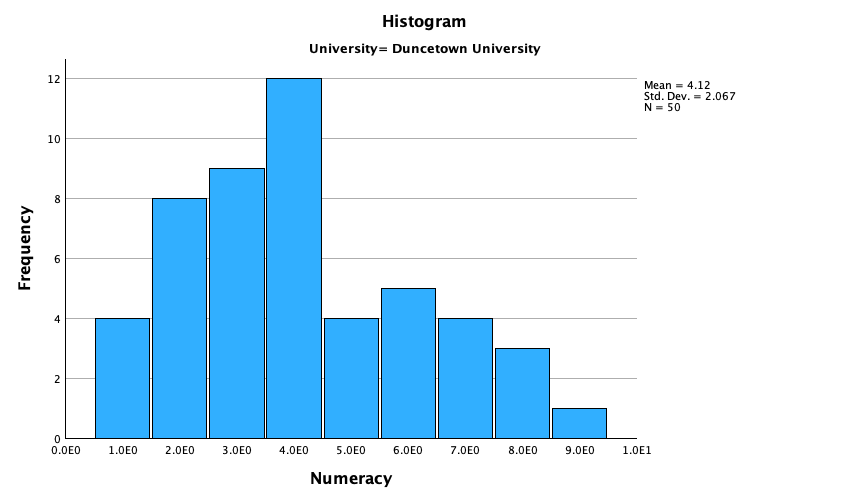
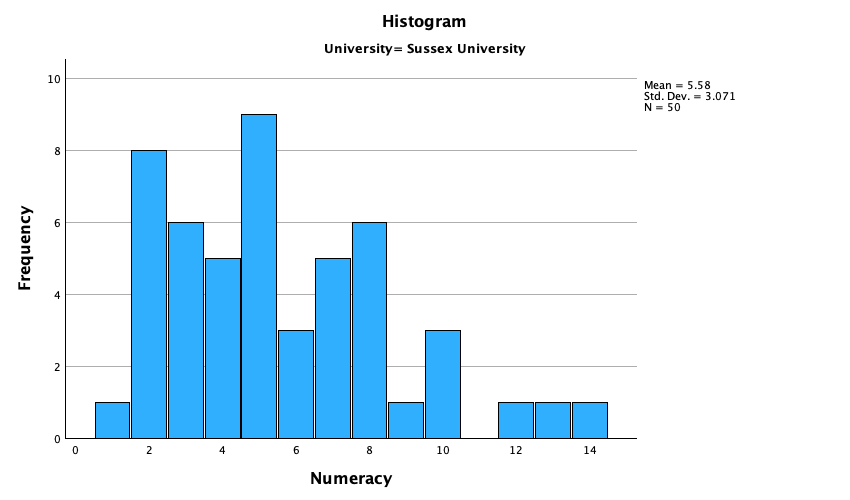
Task 6.6
Repeat Task 5 but for the computer literacy and percentage of lectures attended.
To run the analysis split the file using the instructions in the previous task (Figure 53). Next, Follow the general procedure but drag computer and attendance to the box labelled Dependent List.
The SPSS output is split into two sections: first, the results for students at Duncetown University (Figure 61), then the results for those attending Sussex University (Figure 62). From these tables it is clear that Sussex and Duncetown students scored similarly on computer literacy (both means are very similar). Sussex students attended slightly more lectures (63.27%) than their Duncetown counterparts (56.26%). The histograms are also split according to the university attended. All of the distributions look fairly normal. The only exception is the computer literacy scores for the Sussex students. This is a fairly flat distribution apart from a huge peak between 50 and 60%. It’s slightly heavy-tailed (right at the very ends of the curve the bars come above the line) and very pointy. This suggests positive kurtosis. If you examine the values of kurtosis you will find extreme positive kurtosis as indicated by a value that is more than 2 standard deviations from 0 (i.e. no excess kurtosis), \(z = \frac{1.38}{0.662} = 2.08\).
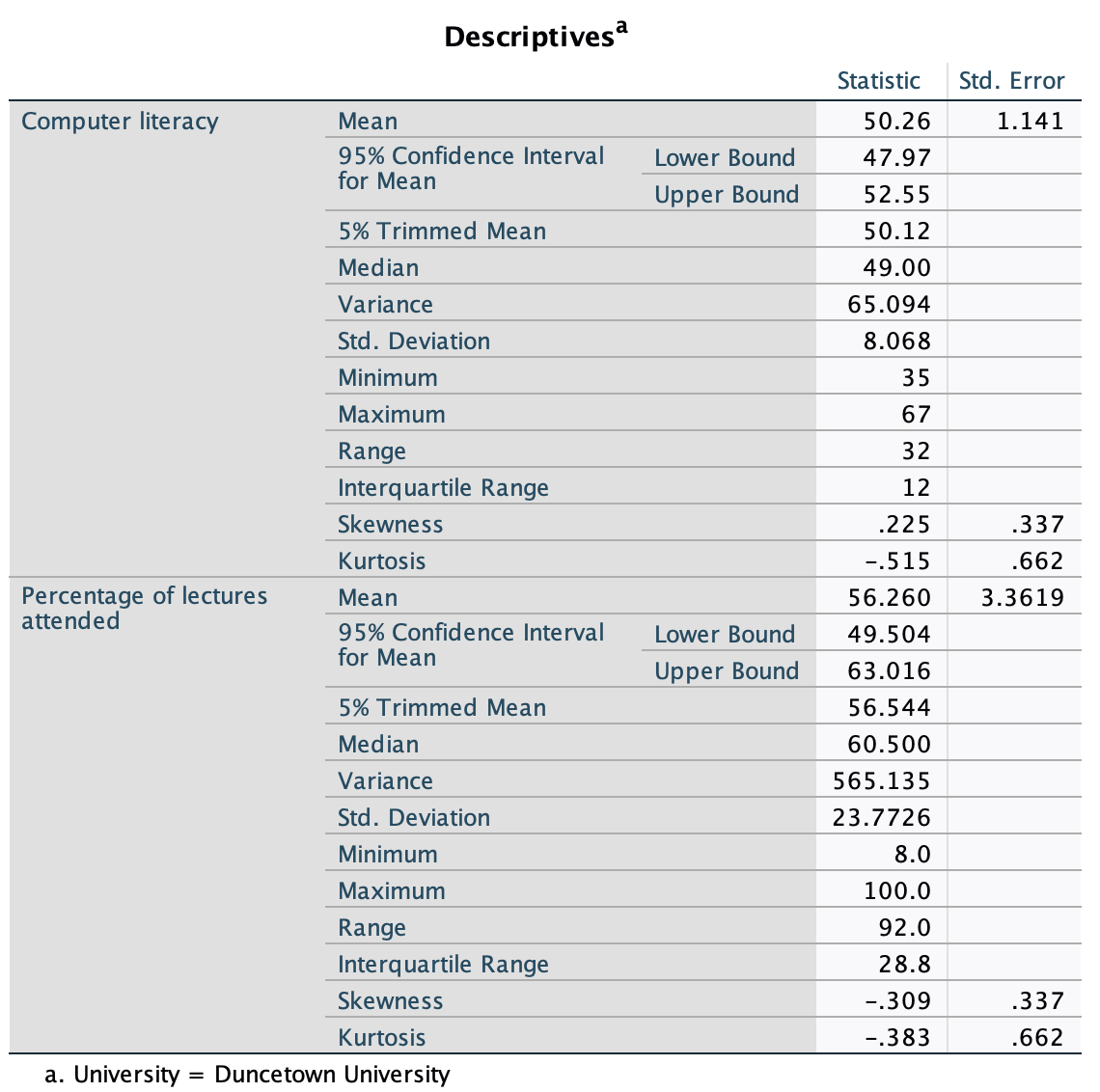
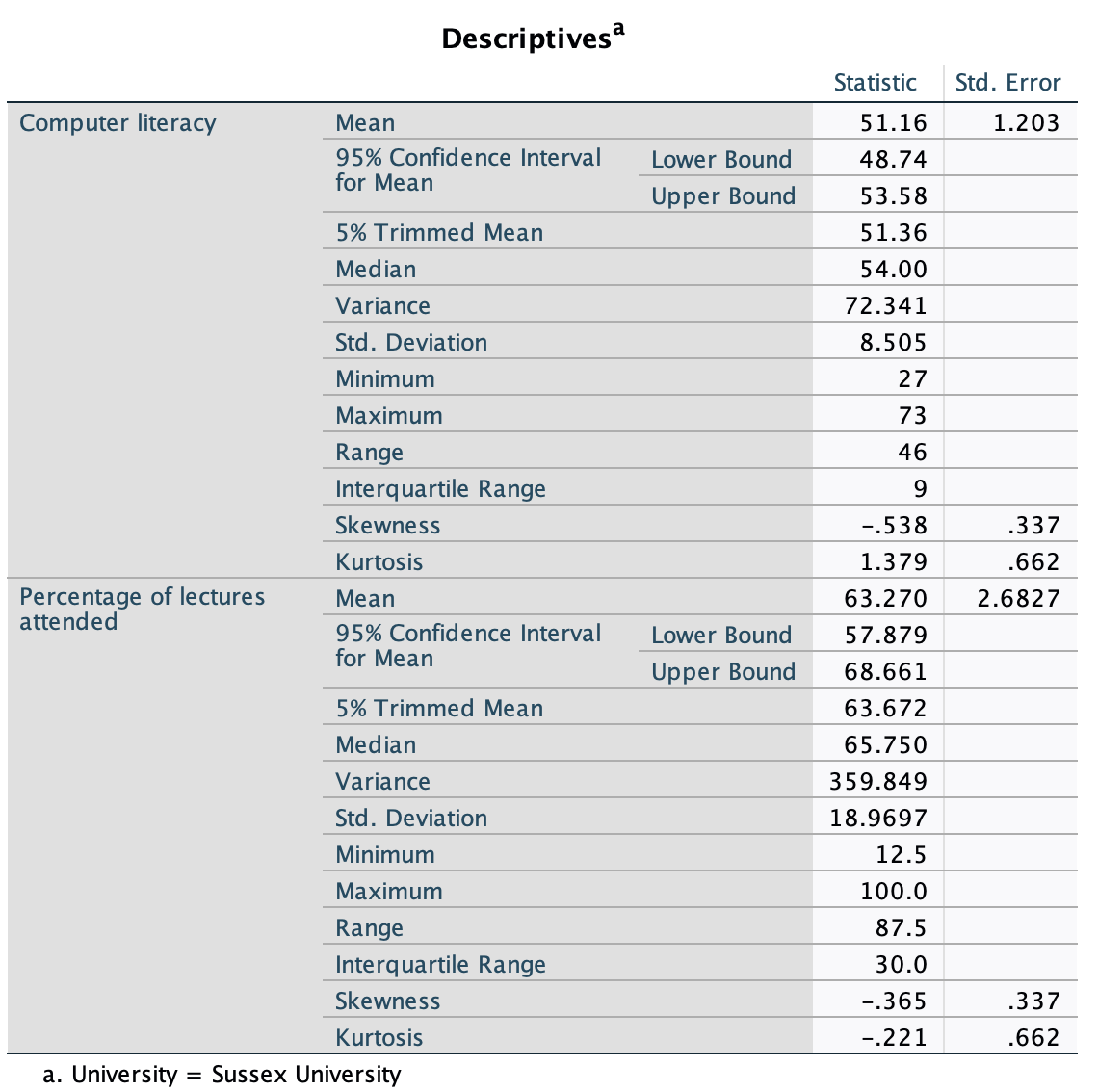
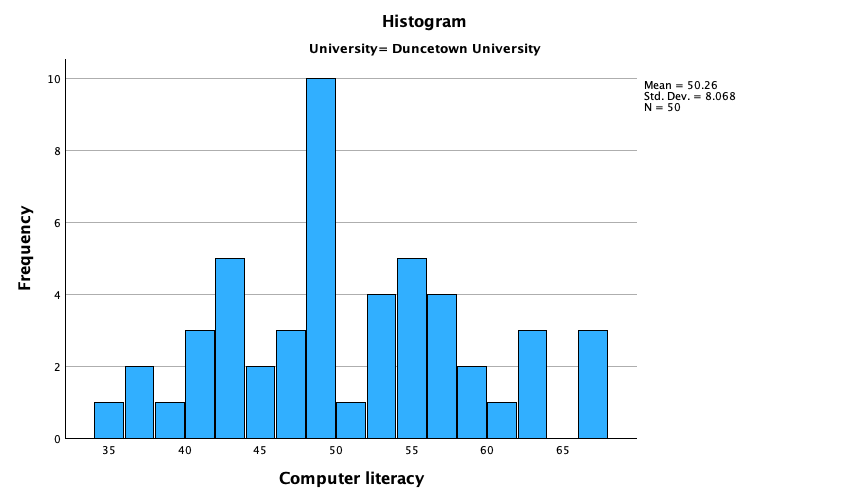
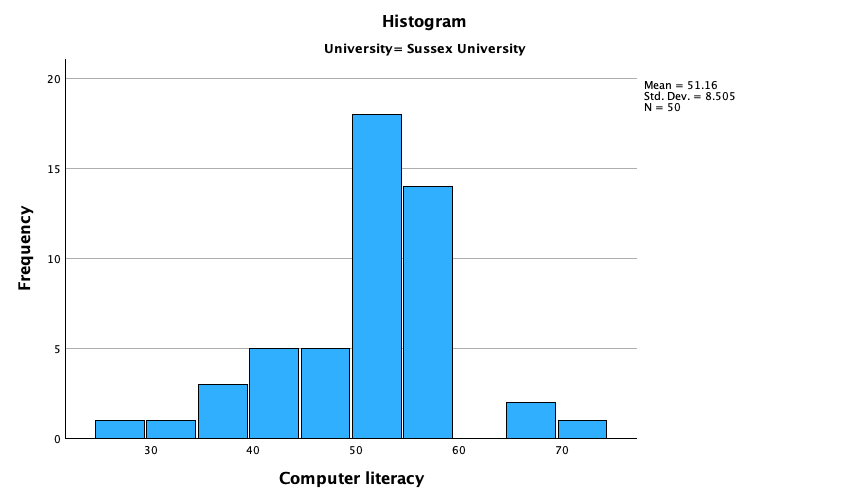
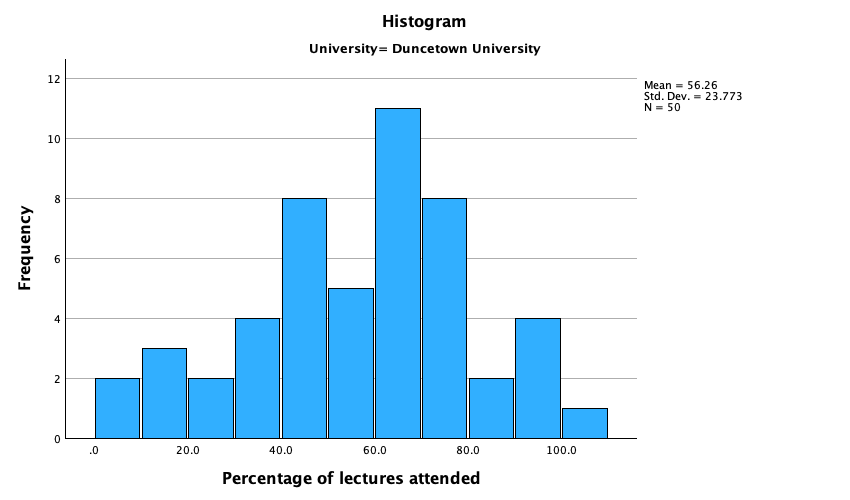
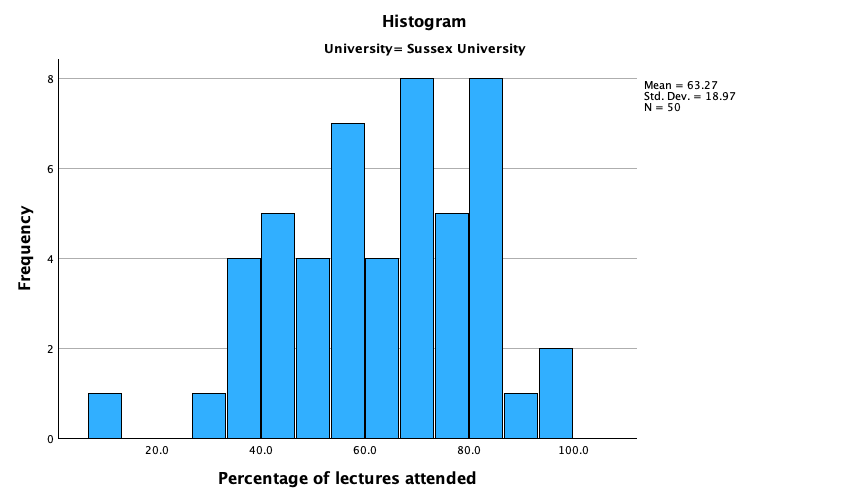
Task 6.7
Conduct and interpret a K-S test for
numeracyandexam.
The correct response to this task should be “but you told me never to do a Kolmogorov–Smirnov test”.
The Kolmogorov–Smirnov (K-S) test can be accessed through the Explore command. Follow the general procedure in Figure 41, but drag exam and numeracy to the box labelled Dependent List. Although we’re not asked to do this, so we won’t, it is possible to select a factor (or grouping variable) by which to split the output. For example, if you drag Uni to the box labelled Factor List, we’ll get a K-S test within each university — a bit like the split file command).

The output containing the K-S test, looks like this:
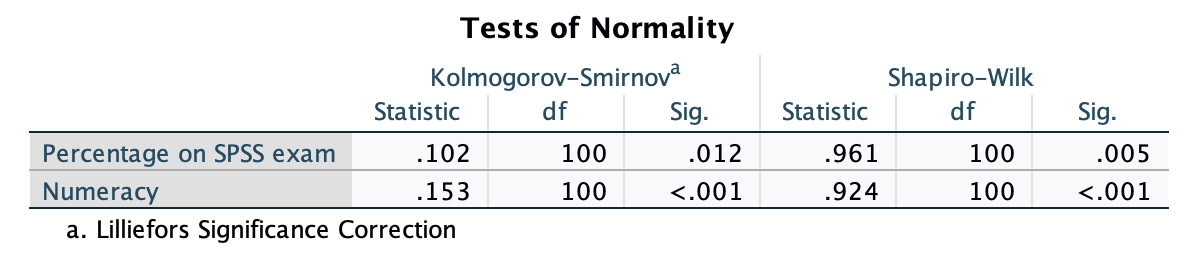
For SPSS exam scores, the K-S test is highly significant, D(100) = 0.10, p = 0.012, and this is true also for numeracy scores, D(100) = 0.15, p < .001. These tests indicate that both distributions are significantly different from normal. This result is likely to reflect the bimodal distribution found for exam scores (#fig-6_2d), and the positively skewed distribution observed in the numeracy scores (fig-6_2g). However, these tests confirm that these deviations were significant (but bear in mind that the sample is fairly big.)
As a final point, bear in mind that when we looked at the exam scores for separate groups, the distributions seemed quite normal; now if we’d asked for separate tests for the two universities (by dragging Uni in the box labelled Factor List) the K-S test will have been different. If you try this out, you’ll get this output:
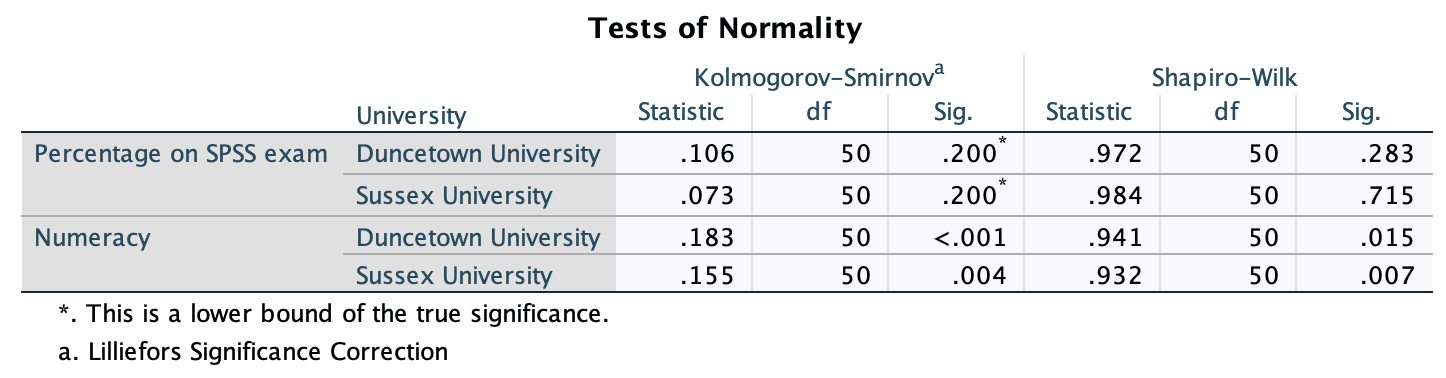
Note that the percentages on the SPSS exam are not significantly different from normal within the two groups. This point is important because if our analysis involves comparing groups, then what’s important is not the overall distribution but the distribution in each group.
Tests like K-S are at the mercy of sample size, so it’s also worth looking at the Q-Q plots. These plots confirm that both variables (overall) are not normal because the dots deviate substantially from the line. (incidentally, the deviation is greater for the numeracy scores, and this is consistent with the higher significance value of this variable on the K-S test.)
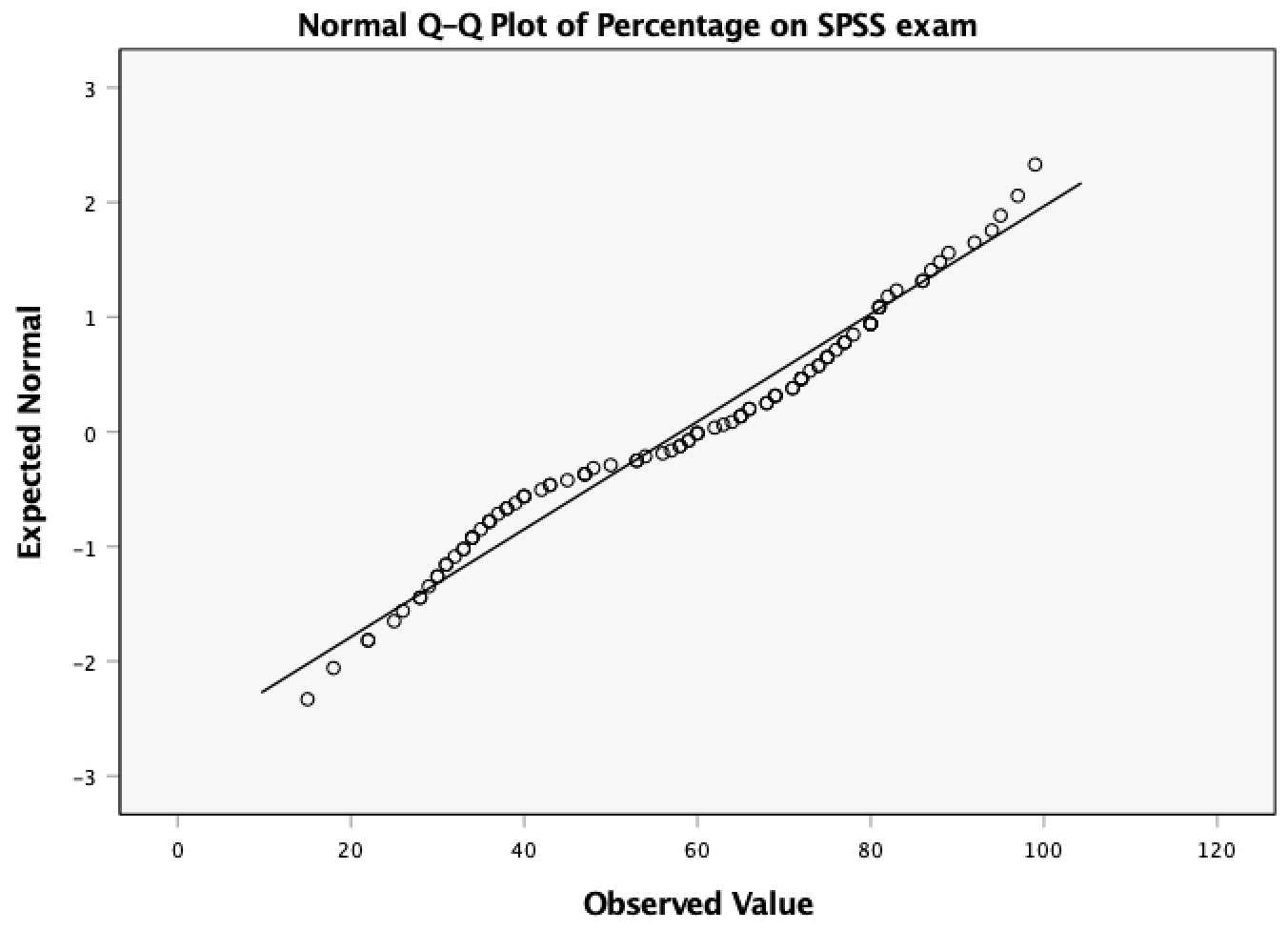
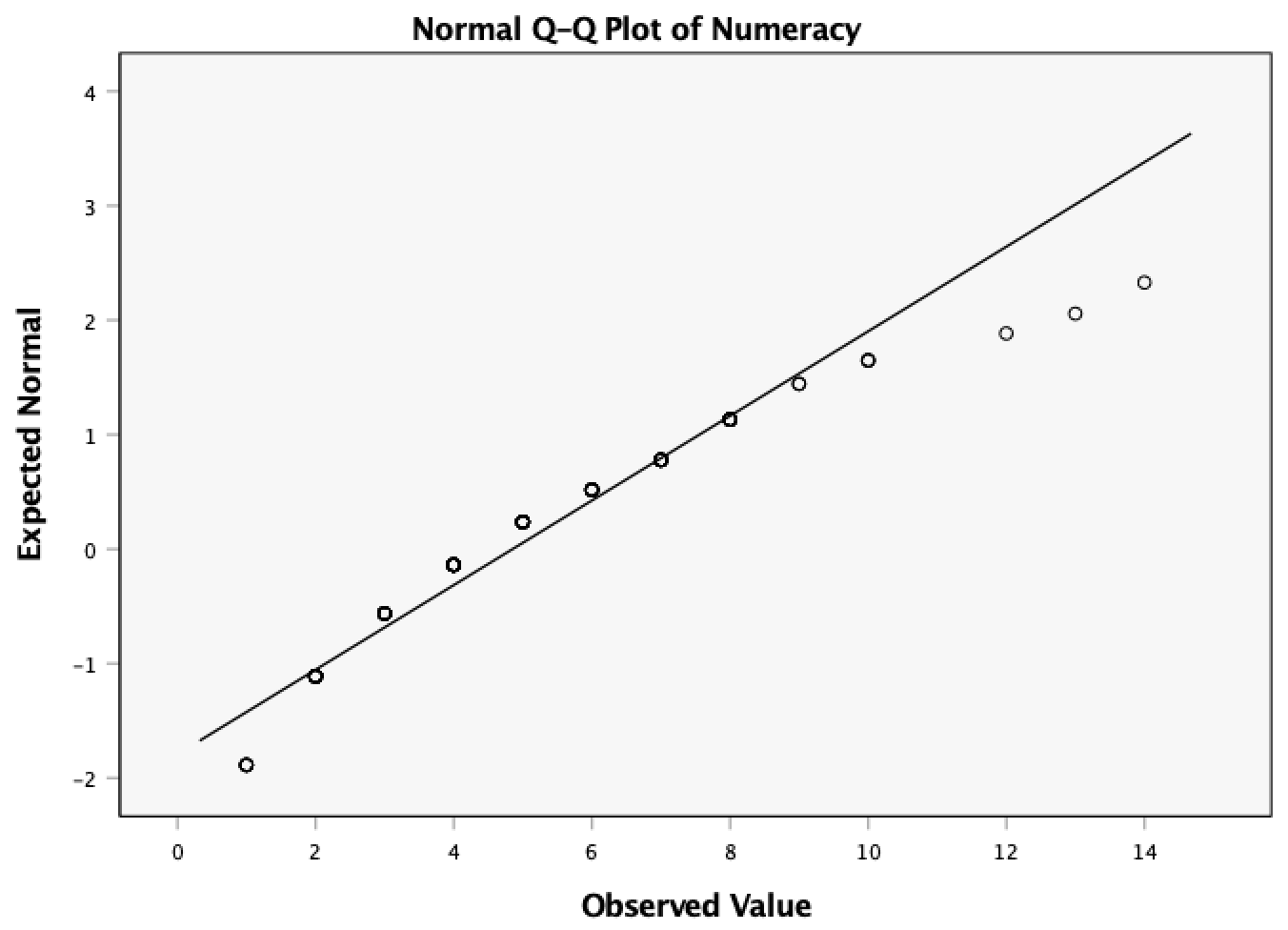
Task 6.8
Conduct and interpret a Levene’s test for
numeracyandexam.
Like the last task, the correct response to this task should be “but you told me never to do Levene’s test”.
Let’s first remind ourselves that Levene’s test is basically pointless (see the book!). Nevertheless, if you insist on consulting it, Levene’s test is obtained using the Explore command. Follow the general procedure in Figure 41, but drag exam and numeracy to the box labelled Dependent List:. To compare variances across the two universities drag the variable Uni to the box labelled Factor List:.
Levene’s test is non-significant for the SPSS exam scores indicating either that that the variances are not significantly different (i.e. they are similar and the homogeneity of variance assumption is tenable) or that the test is underpowered to detect a difference. For the numeracy scores, Levene’s test is significant indicating that the variances are significantly different (i.e., the homogeneity of variance assumption has been violated). We could report that for the percentage on the SPSS exam, the variances for Duncetown and Sussex University students were not significantly different, F(1, 98) = 2.58, p = 0.111, but for numeracy scores the variances were significantly different, F(1, 98) = 7.37, p = 0.008.
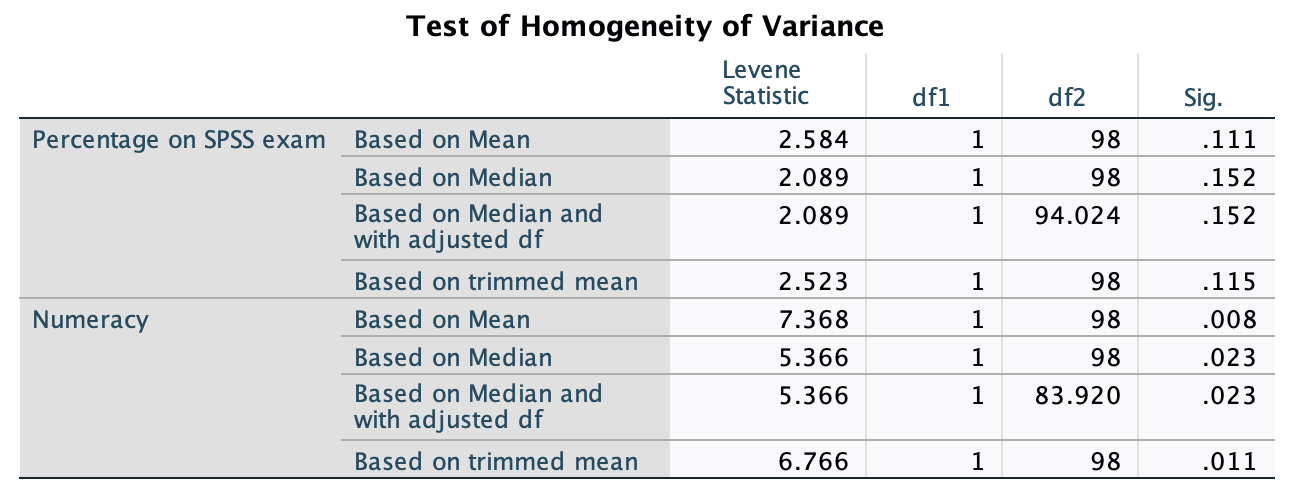
Task 6.9
Transform the
numeracyscores (which are positively skewed) using one of the transformations described in this chapter. Do the data become normal?
Remember to switch off Split File from the previous task.
We can achieve these transformations using the Compute command dialog boxes, but it’s faster to use syntax:
COMPUTE ln_numeracy = LN(numeracy).
COMPUTE sqrt_numeracy = SQRT(numeracy).
COMPUTE recip_numeracy = 1/numeracy.
EXECUTE.Having created these variables, follow the general procedure in Figure 41, but drag numeracy and whatever new variables you have created (in my case ln_numeracy, sqrt_numeracy, and recip_numeracy) to the box labelled Dependent List:.
Below are Q-Q plots of the original scores and the same scores after all three transformations discussed in the book. For each plot we want to compare the distance of the points to the diagonal line to the same distances for the raw scores. For the raw scores (Figure 75) the observed values deviate from normal (the diagonal) at the extremes, but mainly for large observed values (because the distributioon is positively skewed).
- The log transformation (Figure 76) improves the distribution a lot. The positive skew is mitigated by the log transformation (large scores are made less extreme) resulting in dots on the Q-Q plot that are much closer to the line for large observed values.
- Similarly, the square root transformation (Figure 77) mitigates the positive skew too by having a greater effect on large scores. The result is again a Q-Q plot with dots that are much closer to the line for large observed values that for the raw data.
- Conversely, the reciprocal transformation (Figure 78) makes things worse! The result is a Q-Q plot with dots that are much further from the line than for the raw data.
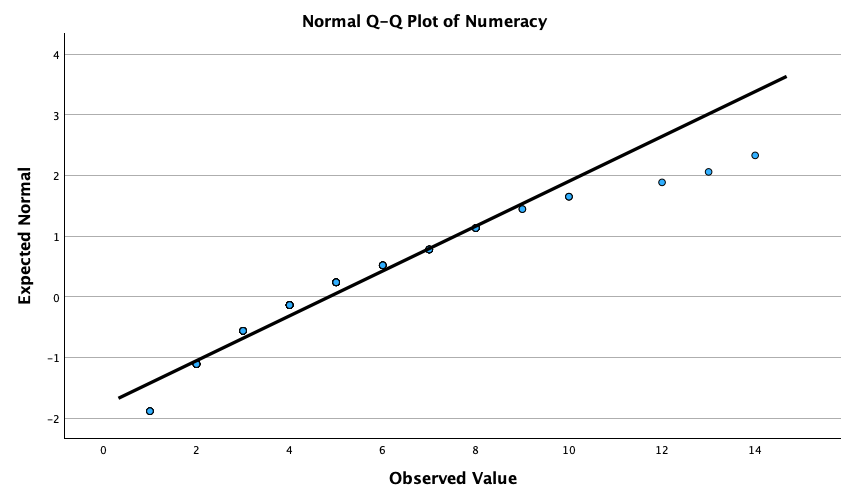
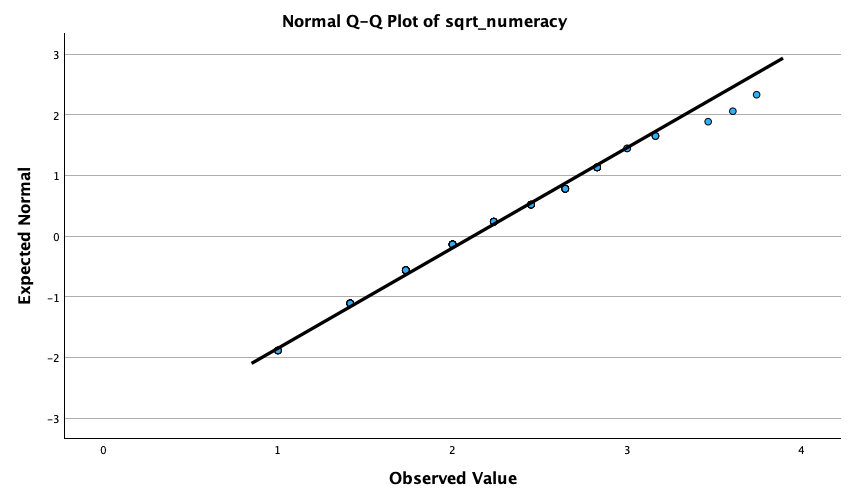
Task 6.10
Use the explore command to see what effect a natural log transformation would have on the four variables measured in
spss_exam.sav.
Follow the general procedure but drag uni to the box labelled Factor List: and the remaining variables to the box labelled Dependent List:. The completed dialog box should look like Figure 79.
Click  and select
and select  and select the default of natural log:
and select the default of natural log:
The output shows Levene’s test on the log-transformed scores. Compare this table to Figure 73 (which was conducted on the untransformed SPSS exam scores and numeracy). To recap, for the untransformed scores Levene’s test was non-significant for the SPSS exam scores (p = 0.111) indicating that the variances were not significantly different (i.e., the homogeneity of variance assumption is tenable). However, for the numeracy scores, Levene’s test was significant (p = 0.008) indicating that the variances were significantly different (i.e. the homogeneity of variance assumption was violated).
For the log-transformed scores (Figure 81), the problem has been reversed: Levene’s test is now significant for the SPSS exam scores (p < 0.001) but is no longer significant for the numeracy scores (p = 0.647). This reiterates my point from the book chapter that transformations are often not a magic solution to problems in the data.
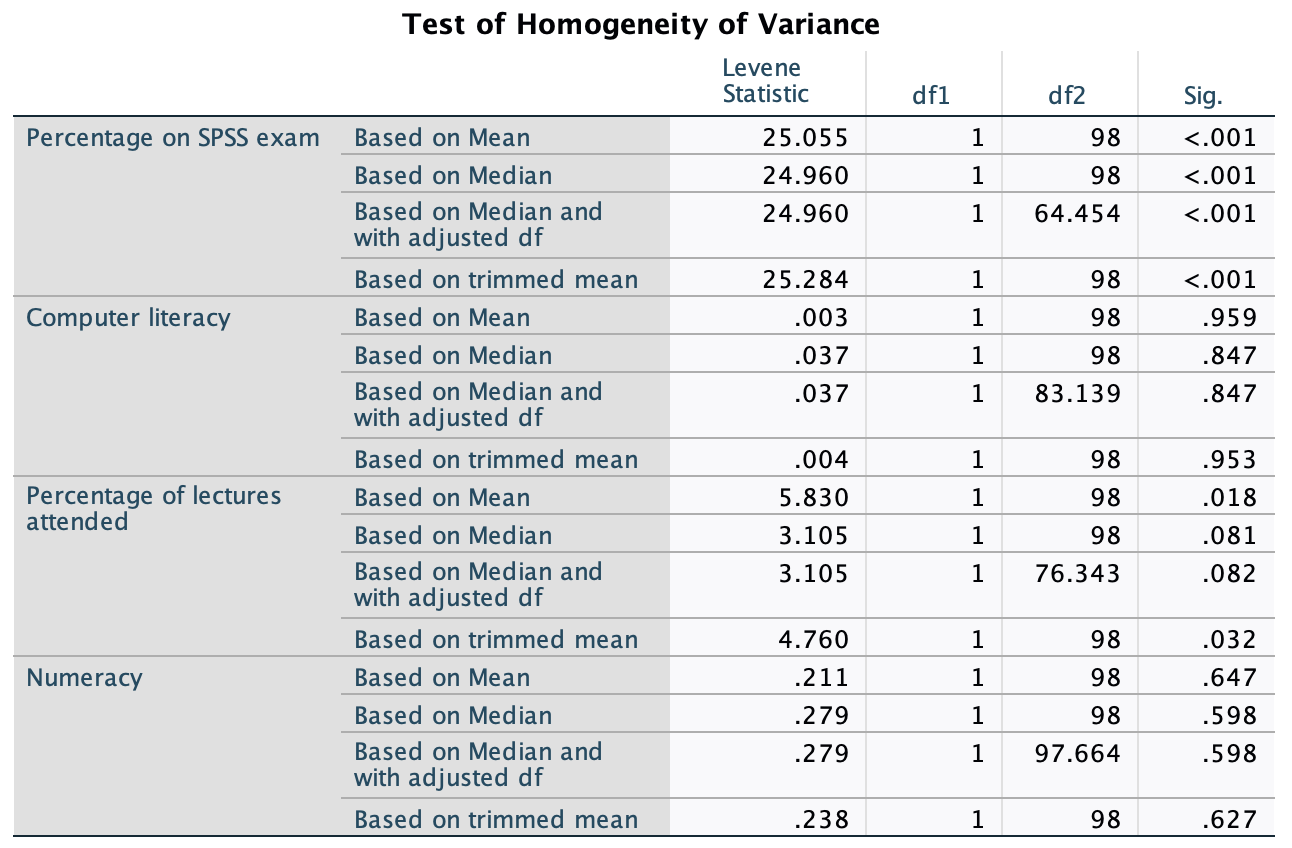
Chapter 7
Task 7.1
A psychologist was interested in the cross-species differences between men and dogs. She observed a group of dogs and a group of men in a naturalistic setting (20 of each). She classified several behaviours as being dog-like (urinating against trees and lampposts, attempts to copulate, and attempts to lick their own genitals). For each man and dog she counted the number of dog-like behaviours displayed in a 24-hour period. It was hypothesized that dogs would display more dog-like behaviours than men. Analyse the data in
men_dogs.savwith a Mann–Whitney test.
We need to conduct a Mann-Whitney test. Figure 82 shows the general procedure. Note that you drag the continuous outcome behaviour to the box labelled Test Fields: and drag the variable that defines the two groups (species) to the area labelled Groups:.

 The output tells us that U is 194.5, and we had 20 men and 20 dogs. The effect size is, therefore:
The output tells us that U is 194.5, and we had 20 men and 20 dogs. The effect size is, therefore:
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} \\ &= 1-\frac{2\times194.5}{20^2} \\ &\simeq 0.0275 \end{aligned} \]
This represents a tiny effect (it is close to zero), which tells us that there truly isn’t much difference between dogs and men.
We could report something like (note I’ve quoted the mean ranks for each group)
Task 7.2
Both Ozzy Osbourne and Judas Priest have been accused of putting backward masked messages on their albums that subliminally influence poor unsuspecting teenagers into doing things like blowing their heads off with shotguns. A psychologist was interested in whether backward masked messages could have an effect. He created a version of Taylor Swift’s ‘Shake it off’ that contained the masked message ‘deliver your soul to the dark lord’ repeated in the chorus. He took this version, and the original, and played one version (randomly) to a group of 32 people. Six months later he played them whatever version they hadn’t heard the time before. So each person heard both the original and the version with the masked message, but at different points in time. The psychologist measured the number of goats that were sacrificed in the week after listening to each version. Test the hypothesis that the backward message would lead to more goats being sacrificed using a Wilcoxon signed-rank test (
dark_lord.sav).
We are comparing scores from the same individuals after exposure to two songs, so we need to use the Wilcoxon signed-rank test. The general procedure is shown in Figure 84. Note that you drag the variables representing the outcomes after hearing the message and nomessage to the box labelled Test Fields:.
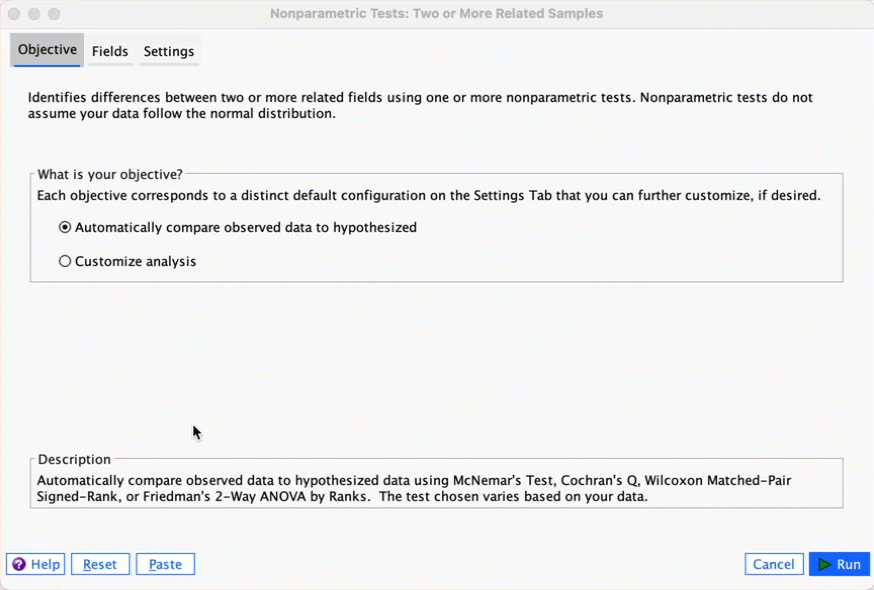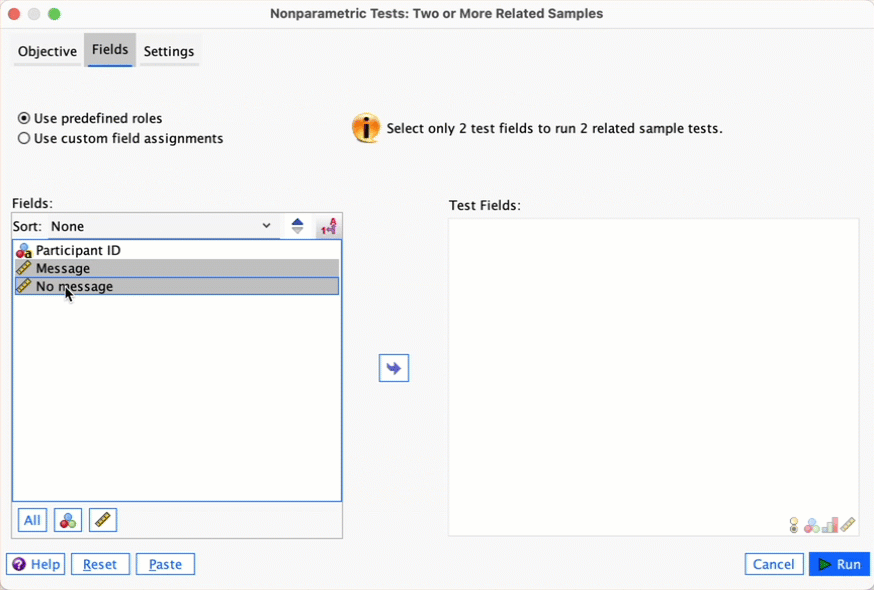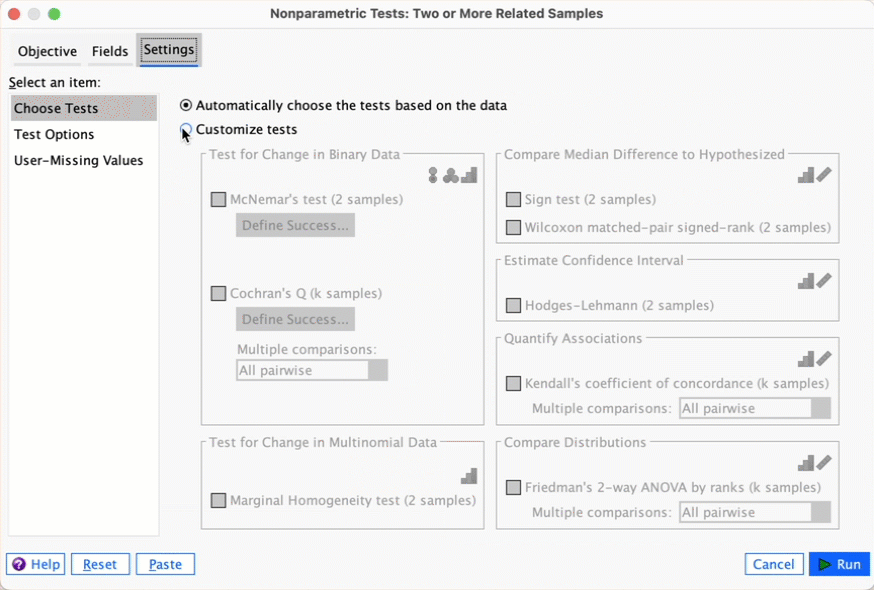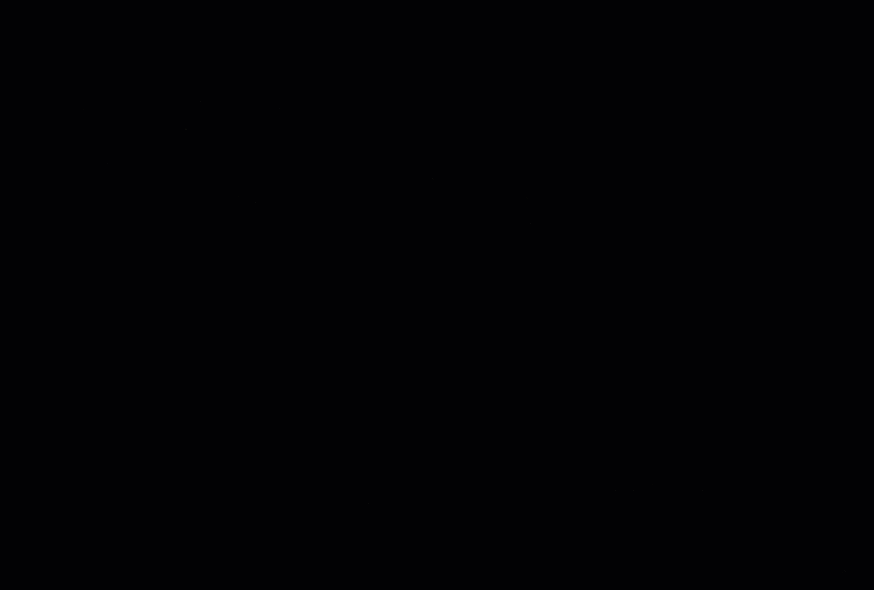
The output is as follows

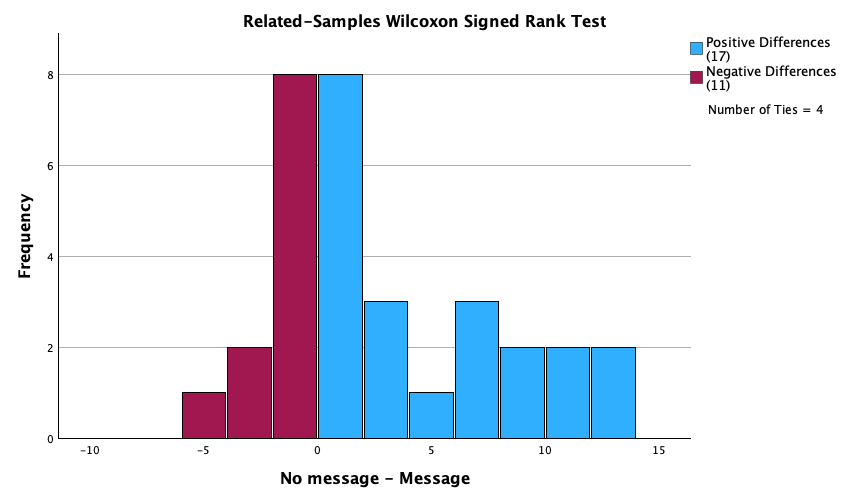
The output tells us that the test statistic is 294.5, and this is the sum of positive ranks so \(T_+ = 294.5\). With 32 participants there were 32 ranks in total and so the sum of all ranks (let’s label this \(T_\text{all}\)) is \(1 + 2 + 3 + \cdots + 32\) or \(T_\text{all} = \sum_{i = 1}^{32} x_i = 528\). The sum of negative ranks is, therefore, \(T_- = T_\text{all}-T_+ = 528 - 294.5 = 233.5\). The effect size is, therefore:
\[ \begin{aligned} r_{rb} &= \frac{T_+ - T_-}{T_+ + T_-} \\ &= \frac{294.5 - 233.5}{528} \\ &\simeq 0.1155303 \end{aligned} \]
From the plot (Figure 86) the ranks are based on subtracting scores for message from scores for no message (we can this from the x-axis). So, a positive rank is where more goats were sacrificed after no message than after a message (i.e. no message > message). This effect size tells us proportionately how many more positive ranks there were than negative ranks (0.12 or 12%). We can interpret the value as 12% more of the data favoured the idea of more goats being sacrificed after hearing a song without a hidden message than one with. We could report something like (note that I’ve quoted the mean ranks):
Task 7.3
A media researcher was interested in the effect of television programmes on domestic life. She hypothesized that through ‘learning by watching’, certain programmes encourage people to behave like the characters within them. She exposed 54 couples to three popular TV shows, after which the couple were left alone in the room for an hour. The experimenter measured the number of times the couple argued. Each couple viewed all TV shows but at different points in time (a week apart) and in a counterbalanced order. The TV shows were EastEnders (a UK TV show which portrays the lives of extremely miserable, argumentative, London folk who spend their lives assaulting each other, lying and cheating), Friends (which portrays unrealistically considerate and nice people who love each other oh so very much—but I love it anyway), and a National Geographic programme about whales (this was a control). Test the hypothesis with Friedman’s ANOVA (
eastenders.sav).
To conduct a Friedman’s ANOVA follow Figure 87. Note that you drag all variables to the box labelled Test Fields:. To get the information for effect sizes execute the following syntax:
NPAR TESTS
/WILCOXON=eastend eastend friends WITH friends whales whales (PAIRED)
/STATISTICS DESCRIPTIVES

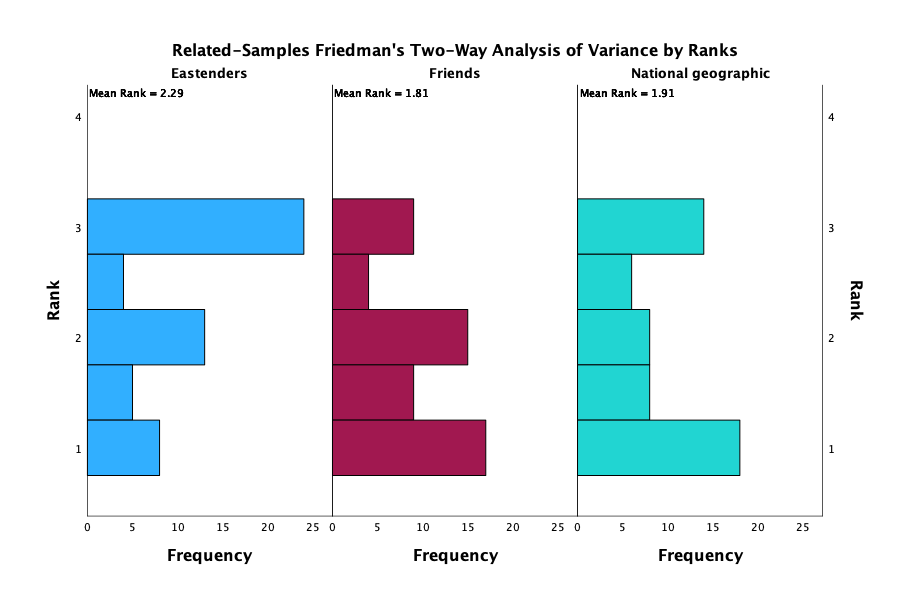
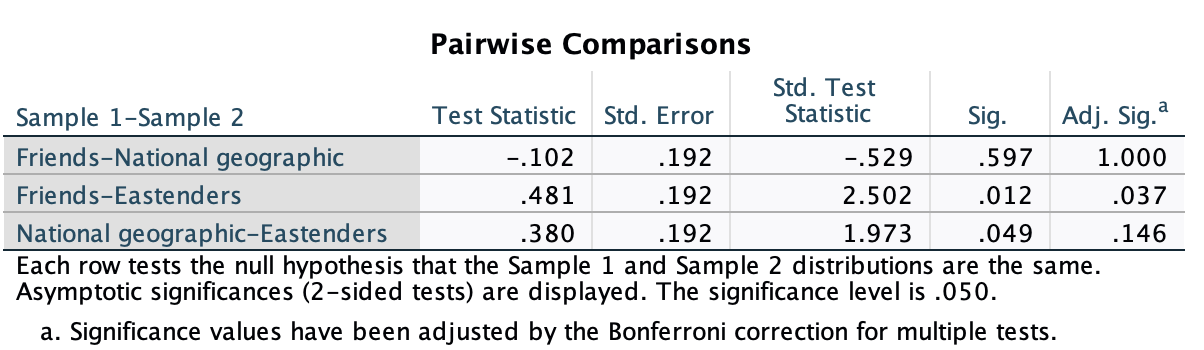
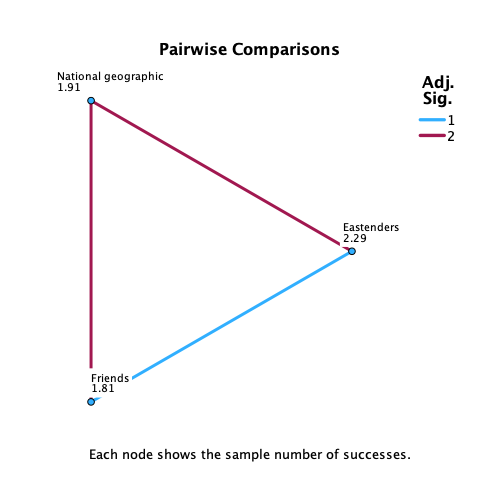
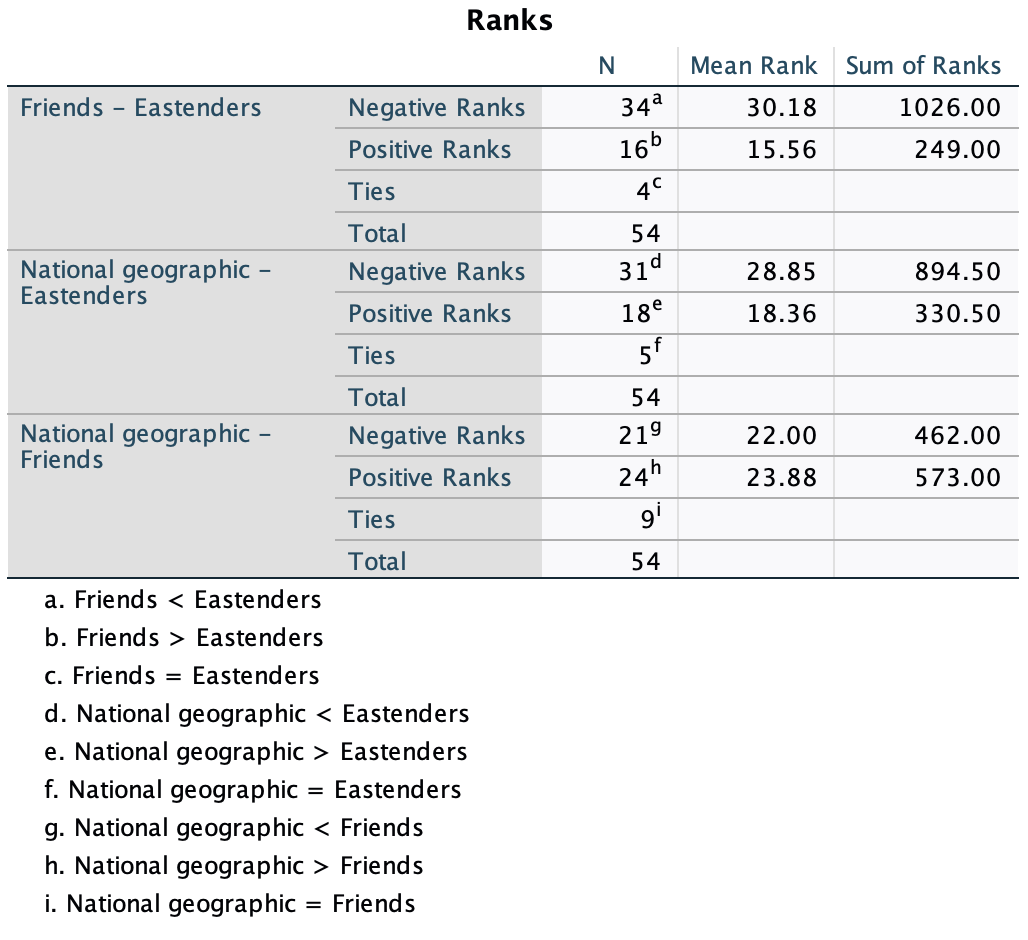
First let’s use Figure 92 to calculate the effect sizes
\[ \begin{aligned} r_{rb} &= \frac{T_+ - T_-}{T_+ + T_-} \\ r_{rb \ (\text{Friends-Eastenders})} &= \frac{249 - 1026}{249 + 1026} &\simeq -0.609 \\ r_{rb \ (\text{Whales-Eastenders})} &= \frac{330.5 - 894.5}{330.5 + 894.5} &\simeq -0.460 \\ r_{rb \ (\text{Whales-Friends})} &= \frac{573 - 462}{573 + 462} &\simeq 0.107 \\ \end{aligned} \]
Now, let’s report everything!
Task 7.4
A researcher was interested in preventing coulrophobia (fear of clowns) in children. She did an experiment in which different groups of children (15 in each) were exposed to positive information about clowns. The first group watched adverts in which Ronald McDonald is seen dancing with children and singing about how they should love their mums. A second group was told a story about a clown who helped some children when they got lost in a forest (what a clown was doing in a forest remains a mystery). A third group was entertained by a real clown, who made balloon animals for the children. A final, control, group had nothing done to them at all. Children rated how much they liked clowns from 0 (not scared of clowns at all) to 5 (very scared of clowns). Use a Kruskal–Wallis test to see whether the interventions were successful (
coulrophobia.sav).
To conduct a Kruskal-Wallis test follow Figure 93. Note that you drag the variable beliefs to the box labelled Test Fields: and infotype to the box labelled Groups:. To get the information for effect sizes execute the following syntax:
NPAR TESTS /M-W= beliefs BY infotype(1 2).
NPAR TESTS /M-W= beliefs BY infotype(1 3).
NPAR TESTS /M-W= beliefs BY infotype(2 3).

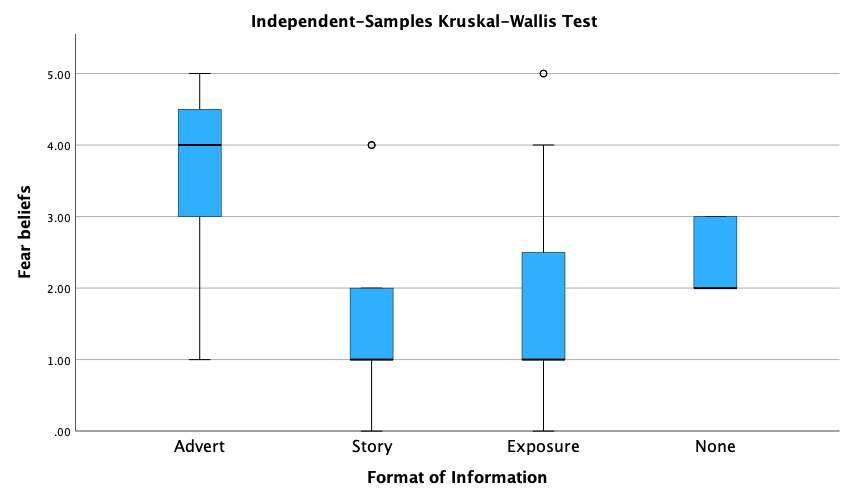
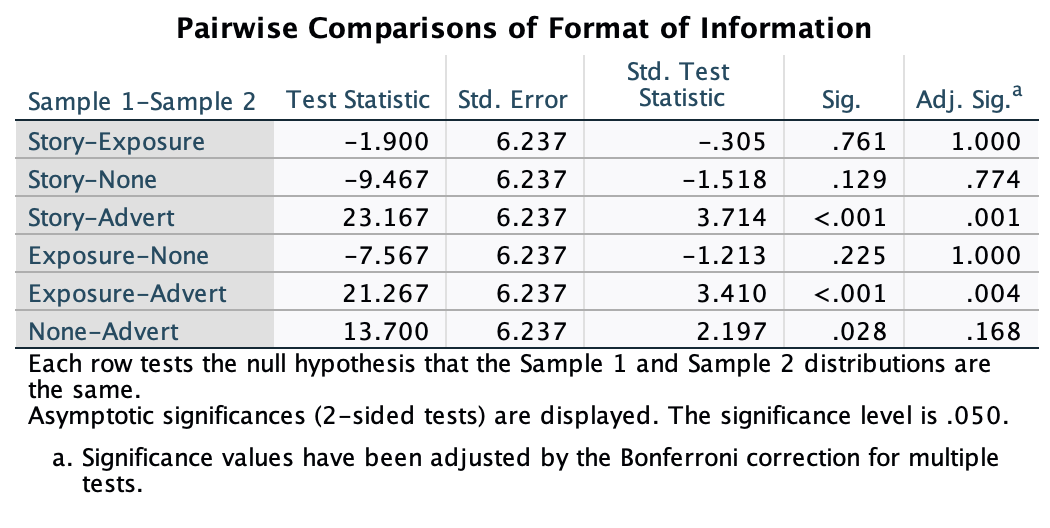
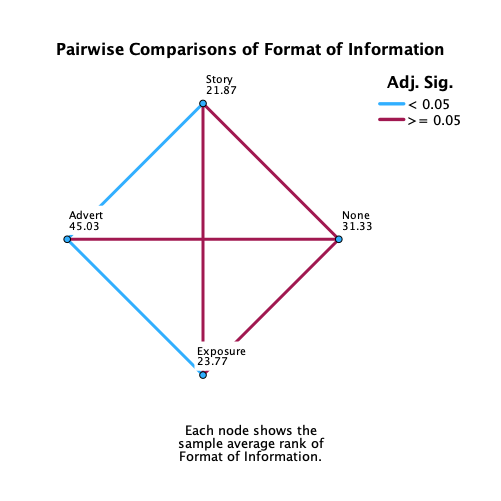
We can conclude that the type of information presented to the children about clowns significantly affected their fear ratings of clowns. The boxplot in the output above gives us an indication of the direction of the effects, but to see where the significant differences lie we need to look at the pairwise comparisons, and calculate the effect sizes (note that \(n\) = 15 in every group, so the denominator is always \(n_1n_2 = 15^2 = 225\)). I haven’t reproduced the Mann-Whitney test outputs but you should find:
- \(U_\text{Advert-Story} = 35.5\)
- \(U_\text{Advert-Exposure} = 46.5\)
- \(U_\text{Advert-None} = 37.5\)
- \(U_\text{Story-Exposure} = 107.5\)
- \(U_\text{Story-None} = 65\)
- \(U_\text{Exposure-None} = 72.5\)
Therefore,
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} \\ r_{pb\text{ (Advert-Story)}} &= 1-\frac{2\times 35.5}{225} &\simeq 0.684 \\ r_{pb\text{ (Advert-Exposure)}} &= 1-\frac{2\times 46.5}{225} &\simeq 0.587 \\ r_{pb\text{ (Story-None)}} &= 1-\frac{2\times 37.5}{225} &\simeq 0.667 \\ r_{pb\text{ (Story-Exposure)}} &= 1-\frac{2\times 107.5}{225} &\simeq 0.044 \\ r_{pb\text{ (Advert-None)}} &= 1-\frac{2\times 65}{225} &\simeq 0.422 \\ r_{pb\text{ (Exposure-None)}} &= 1-\frac{2\times 72.5}{225} &\simeq 0.356 \\ \end{aligned} \]
None of these are inconsequential effects.
Task 7.5
Thinking back to Labcoat Leni’s Real Research 4.1, test whether the number of offers was significantly different in people listening to Bon Scott compared to those listening to Brian Johnson (
acdc.sav). Compare your results to those reported by Oxoby (2008).
We need to conduct a Mann–Whitney test because we want to compare scores in two independent samples: participants who listened to Bon Scott vs. those who listened to Brian Johnson. Figure 82 shows the general procedure. Follow that but drag offers to the box labelled Test Fields: and drag the variable that defines the two groups (singer) to the area labelled Groups:.
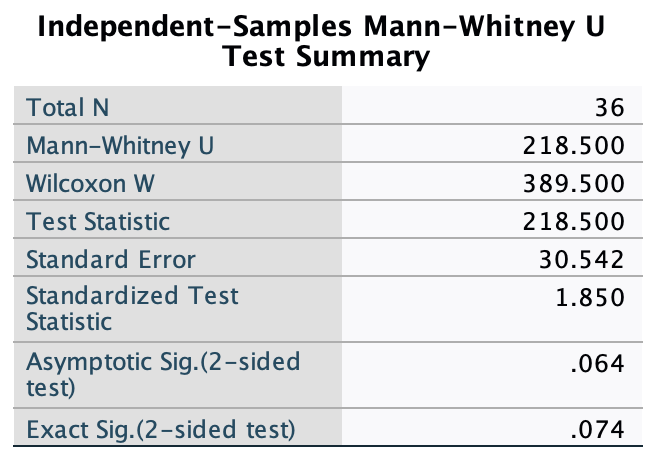
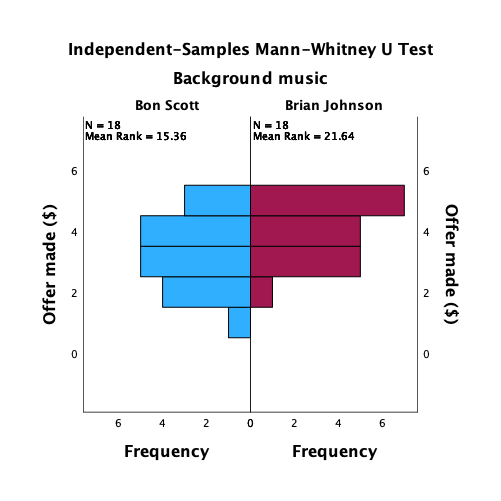
The output tells us that U is 218.5, and we had 18 people who listened to each singer (n_1 = n_2 = 18). The effect size is, therefore:
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} \\ &= 1-\frac{2 \times 218.5}{18^2} \\ &\simeq -0.3487654 \end{aligned} \]
This represents a medium effect: when listening to Brian Johnson people proposed higher offers than when listening to Bon Scott, suggesting that they preferred Brian Johnson to Bon Scott. Although this effect has some substance, it was not significant, which shows that a fairly substantial effect size can be non-significant in a small sample. We could report something like (note that I’ve quoted the mean ranks):
Task 7.6
Repeat the analysis above, but using the minimum acceptable offer – see Chapter 4, Task 3.
We again conduct a Mann–Whitney test. This is because we are comparing two independent samples (those who listened to Brian Johnson and those who listened to Bon Scott). Figure 82 shows the general procedure. Follow that but drag moa to the box labelled Test Fields: and drag the variable that defines the two groups (singer) to the area labelled Groups:.
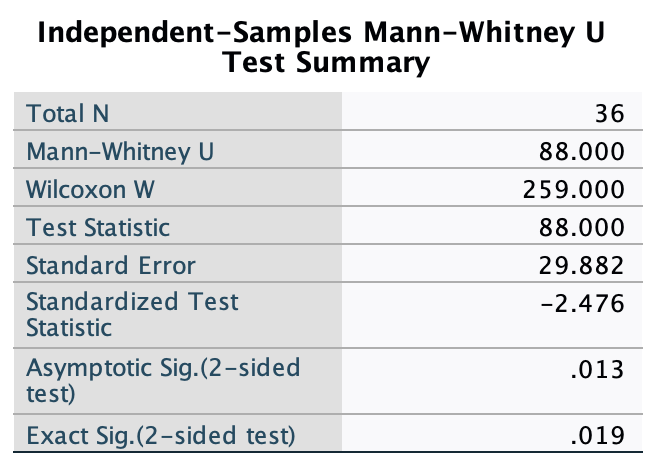
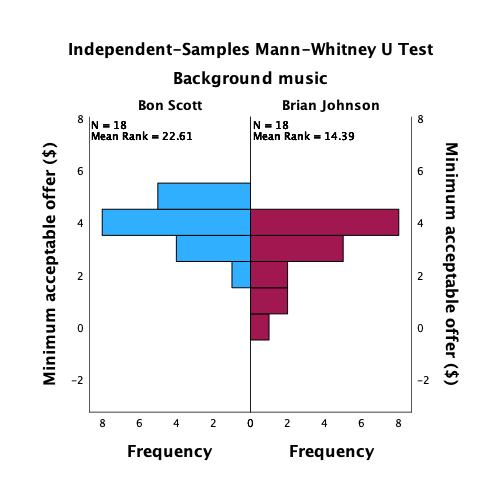
The output tells us that U is 88, and we had 18 people who listened to each singer (n_1 = n_2 = 18). The effect size is, therefore:
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} \\ &= 1-\frac{2 \times 88}{18^2} \\ &\simeq 0.4567901 \end{aligned} \]
This represents a fairly strong effect: looking at the mean ranks in the output above, we can see that people accepted lower offers when listening to Brian Johnson than when listening to Bon Scott. We could report something like (note that I’ve quoted the mean ranks):
Task 7.7
Using the data in
shopping.sav(Chapter 4, Task 4), test whether men and women spent significantly different amounts of time shopping?
We need to conduct a Mann–Whitney test because we are comparing two independent samples (men and women). Figure 82 shows the general procedure. Follow that but drag time to the box labelled Test Fields: and drag the variable that defines the two groups (sex) to the area labelled Groups:.

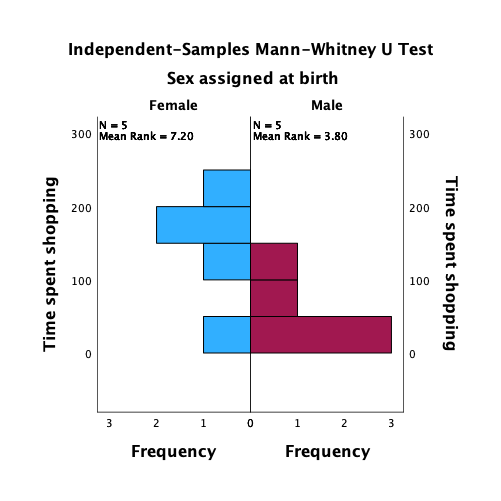
The output tells us that U is 21, and we had 5 men and women (n_1 = n_2 = 5). The effect size is, therefore:
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} \\ &= 1-\frac{2 \times 21}{5^2} \\ &\simeq -0.68 \end{aligned} \]
This represents a large effect, which highlights how large effects can be non-significant in small samples. The mean ranks show that women spent more time shopping than men. We could report something like (note that I’ve quoted the mean ranks):
Task 7.8
Using the same data, test whether men and women walked significantly different distances while shopping.
Again, we conduct a Mann–Whitney test because – yes, you guessed it – we are once again comparing two independent samples (men and women). Figure 82 shows the general procedure. Follow that but drag distance to the box labelled Test Fields: and drag the variable that defines the two groups (sex) to the area labelled Groups:.
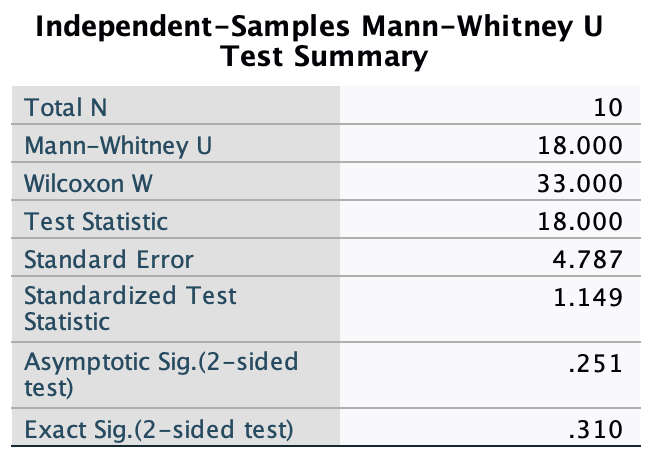
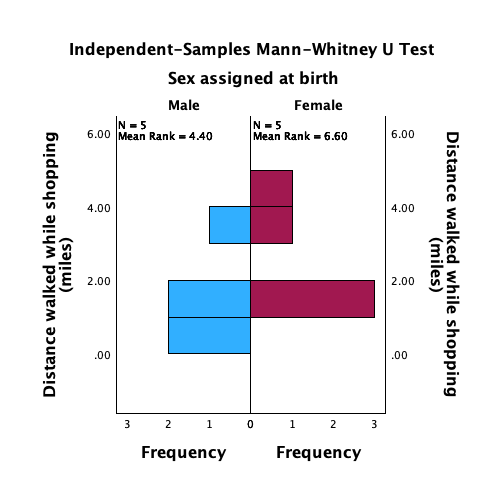
The output tells us that U is 18, and we had 5 men and women (n_1 = n_2 = 5). The effect size is, therefore:
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} \\ &= 1-\frac{2 \times 18}{5^2} \\ &\simeq -0.44 \end{aligned} \]
Again this represents a fairly strong effect, and highlights how large effects can be non-significant in small samples. The mean ranks show that women spent more time shopping than men. We could report something like (note that I’ve quoted the mean ranks):
Task 7.9
Using the data in
pets.sav(Chapter 4, Task 5), test whether people with fish or cats as pets differed significantly in their life satisfaction.
To answer this question we run a Mann–Whitney test. The reason for choosing this test is that we are comparing two independent groups (people with fish or cats as pets). Figure 82 shows the general procedure. Follow that but drag moa to the box labelled Test Fields: and drag the variable that defines the two groups (singer) to the area labelled Groups:.
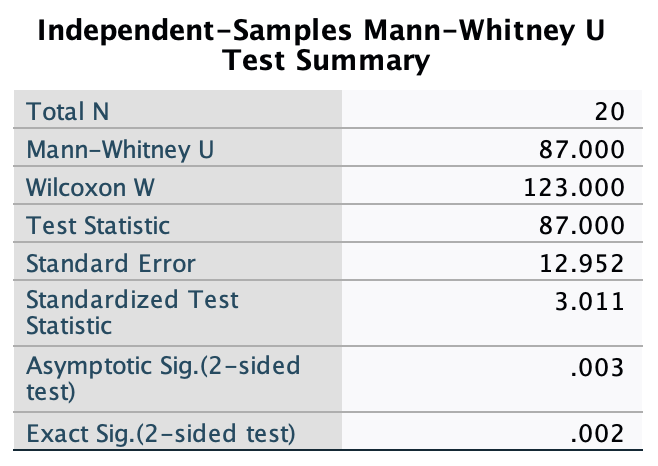
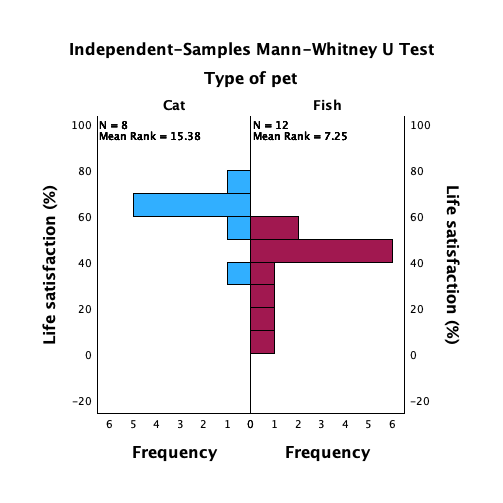
The output tells us that U is 87, and we had 12 fish owners (\(n_1 = 12\)) and 8 cat owners (\(n_2 = 8\)). The effect size is, therefore:
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} \\ &= 1-\frac{2 \times 87}{ 12\times 8} \\ &\simeq -0.8125 \end{aligned} \]
This represents a very strong effect: looking at the mean ranks in the output above, we can see that life satisfaction was higher in those who had cats for a pet. We could report something like (note that I’ve quoted the mean ranks):
Task 7.10
Use the
spss_exam.sav(Chapter 6, Task 2) data to test whether students at the Universities of Sussex and Duncetown differed significantly in their SPSS exam scores, their numeracy, their computer literacy, and the number of lectures attended.
To answer this question run a series of Mann–Whitney tests. The reason for choosing this test is that we are comparing two unrelated groups (students who attended Sussex University and students who attended Duncetown University).
The outputs are below
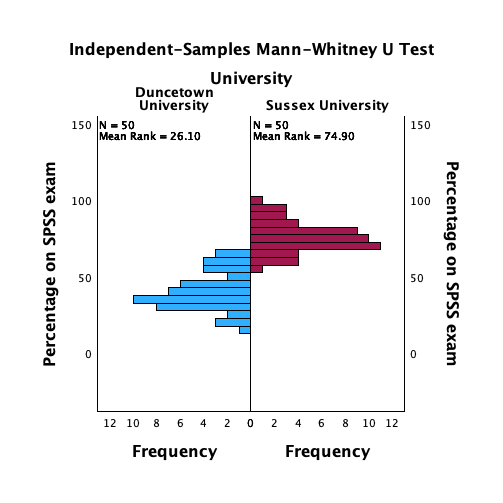
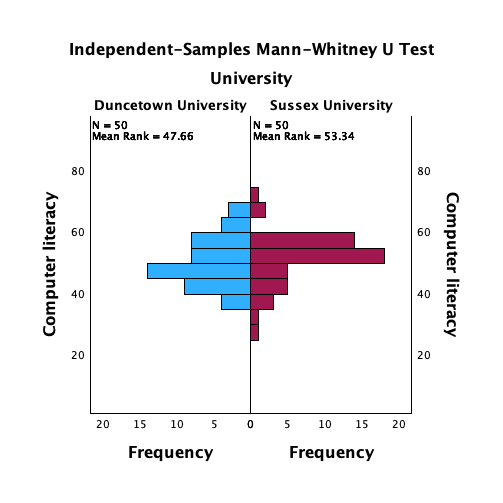
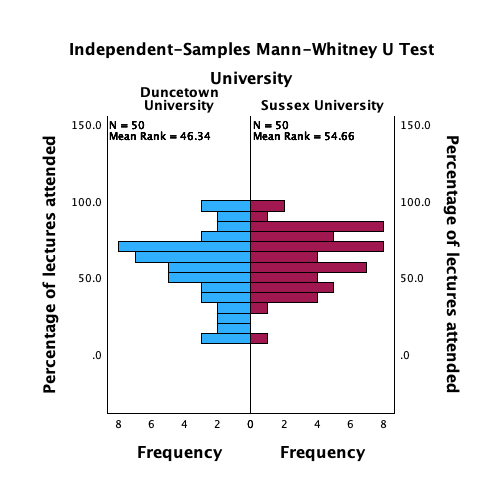
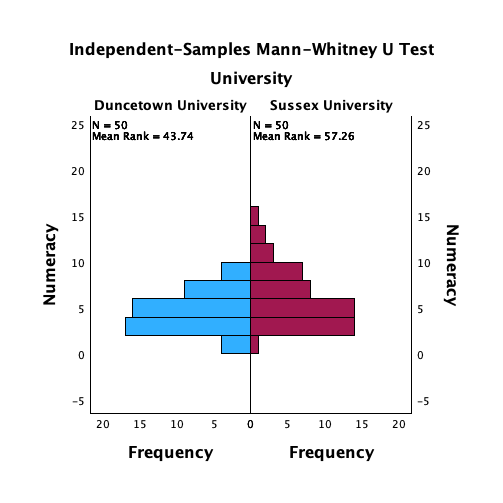
Let’s calculate the effect sizes for the difference between Duncetown and Sussex universities for each outcome. In each case there are 50 students from each university so \(n_1 = n_2 = 50\). From the outputs \(U\) = 2470 for exam scores (Figure 105), \(U\) = 1392 for computer literacy (Figure 107), \(U\) = 1458 for lecture attendance (Figure 109) and \(U\) = 1588 for numeracy (Figure 111).
\[ \begin{aligned} r_{rb} &= 1-\frac{2U}{n_1 n_2} = 1-\frac{2U}{50\times 50}\\ r_{rb \text{ (SPSS exam)}} &= 1-\frac{2 \times 2470}{50^2} = -0.976 \\ r_{rb \text{ (Computer literacy)}} &= 1-\frac{2 \times 1392}{50^2} = -0.1136 \\ r_{rb \text{ (Lecture attendance)}} &= 1-\frac{2 \times 1458}{50^2} = -0.1664 \\ r_{rb \text{ (Numeracy)}} &= 1-\frac{2 \times 1588}{50^2} = -0.2704 \\ \end{aligned} \]
Task 7.11
Use the
download.savdata from Chapter 6 to test whether hygiene levels changed significantly over the three days of the festival.
Conduct a Friedman’s ANOVA because we want to compare more than two (day 1, day 2 and day 3) related samples (the same participants were used across the three days of the festival). To run the analysis follow Figure 87 noting that you drag day_1, day_2 and day_3 to the box labelled Test Fields:. To get the information for effect sizes execute the following syntax:
NPAR TESTS
/WILCOXON=day_1 day_1 day_2 WITH day_2 day_3 day_3 (PAIRED)
/STATISTICS DESCRIPTIVES
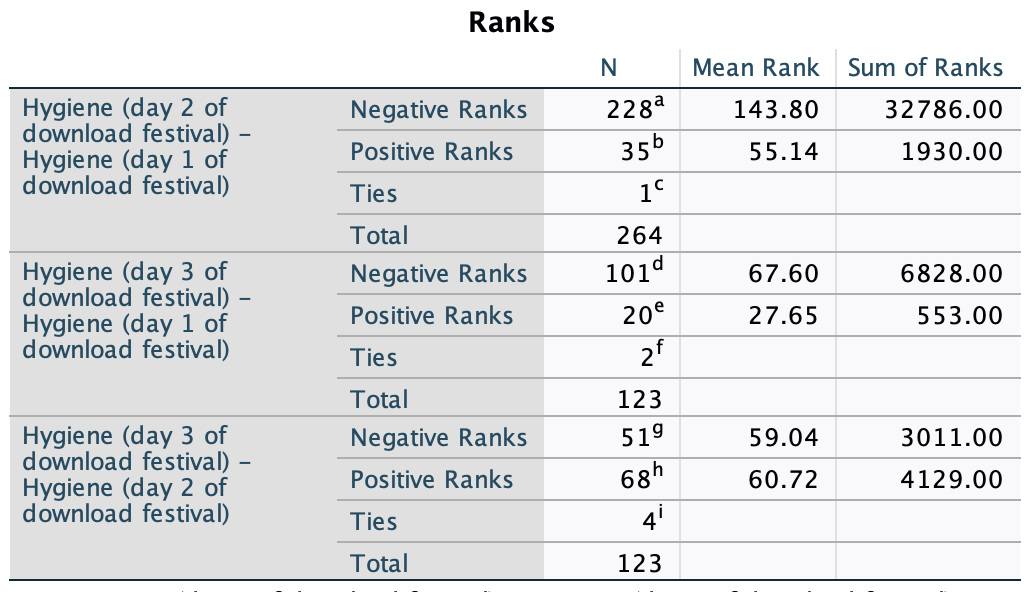
First let’s use Figure 117 to calculate the effect sizes
\[ \begin{aligned} r_{rb} &= \frac{T_+ - T_-}{T_+ + T_-} \\ r_{rb \ (\text{Day 1-Day 2})} &= \frac{1930 - 32786}{1930 + 32786} &\simeq -0.889 \\ r_{rb \ (\text{Day 1-Day 3})} &= \frac{553 - 6828}{553 + 6828} &\simeq -0.850 \\ r_{rb \ (\text{Day 2-Day 3})} &= \frac{4129 - 3011}{4129 + 3011} &\simeq 0.157 \\ \end{aligned} \]
Now, let’s report everything!
Chapter 8
Task 8.1
A student was interested in whether there was a positive relationship between the time spent doing an essay and the mark received. He got 45 of his friends and timed how long they spent writing an essay (hours) and the percentage they got in the essay (
essay). He also translated these grades into their degree classifications (grade): in the UK, a student can get a first-class mark (the best), an upper-second-class mark, a lower second, a third, a pass or a fail (the worst). Using the data in the fileessay_marks.savfind out what the relationship was between the time spent doing an essay and the eventual mark in terms of percentage and degree class (draw a scatterplot too).
We’re interested in looking at the relationship between hours spent on an essay and the grade obtained. We could create a scatterplot of hours spent on the essay (x-axis) and essay mark (y-axis). I’ve chosen to highlight the degree classification grades using different colours. The resulting scatterplot is in Figure 118.
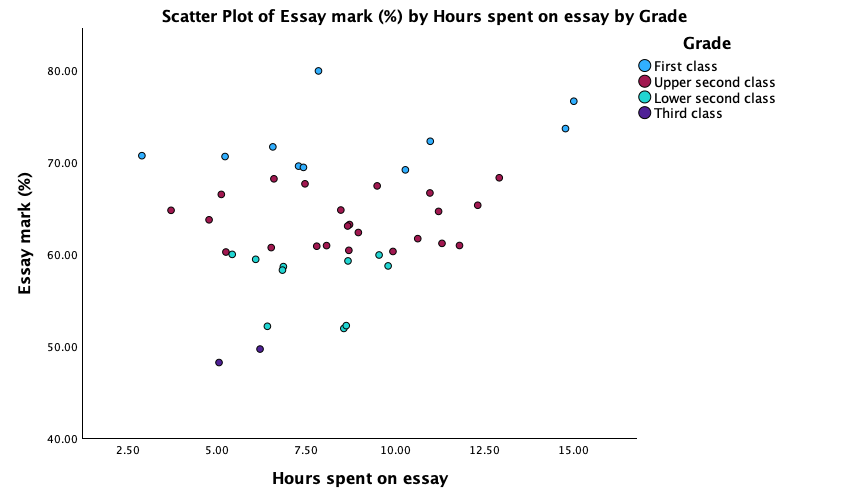
We can use the Explore menu to look at the distributions of scores. The Q-Q plots (Figure 119 and Figure 120) both look fairly normal.
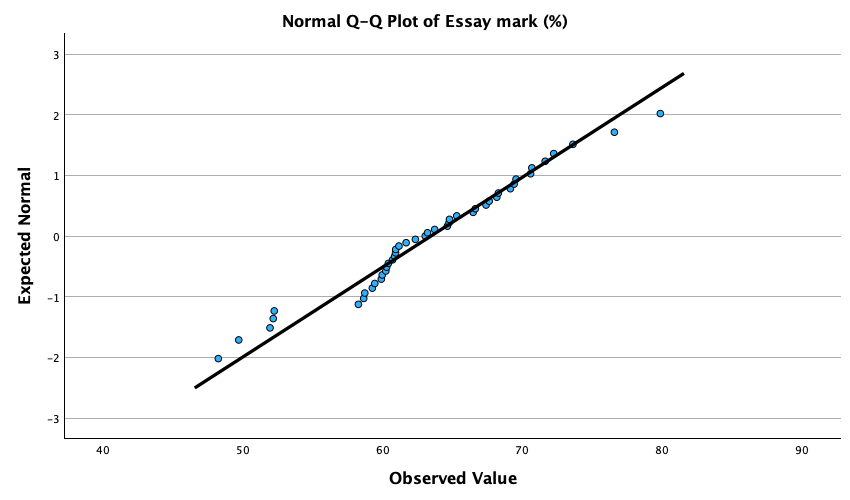
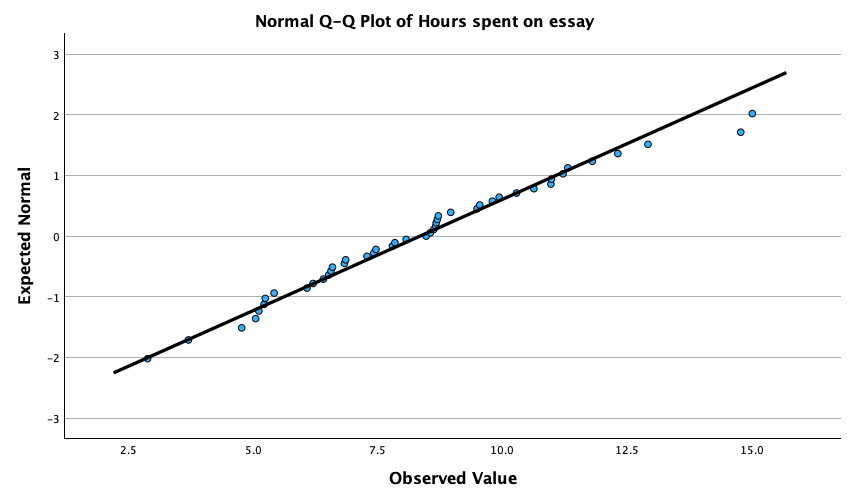
On balance, we can probably use Pearson’s correlation coefficient. I chose a two-tailed test because it is never really appropriate to conduct a one-tailed test (see the book chapter). I also requested the bootstrapped confidence intervals even though the data were normal because they are robust. The results in Figure 121 above indicate that the relationship between time spent writing an essay and grade awarded was not significant, Pearson’s r = 0.27, 95% BCa CI [-0.018, 0.506], p = 0.077.
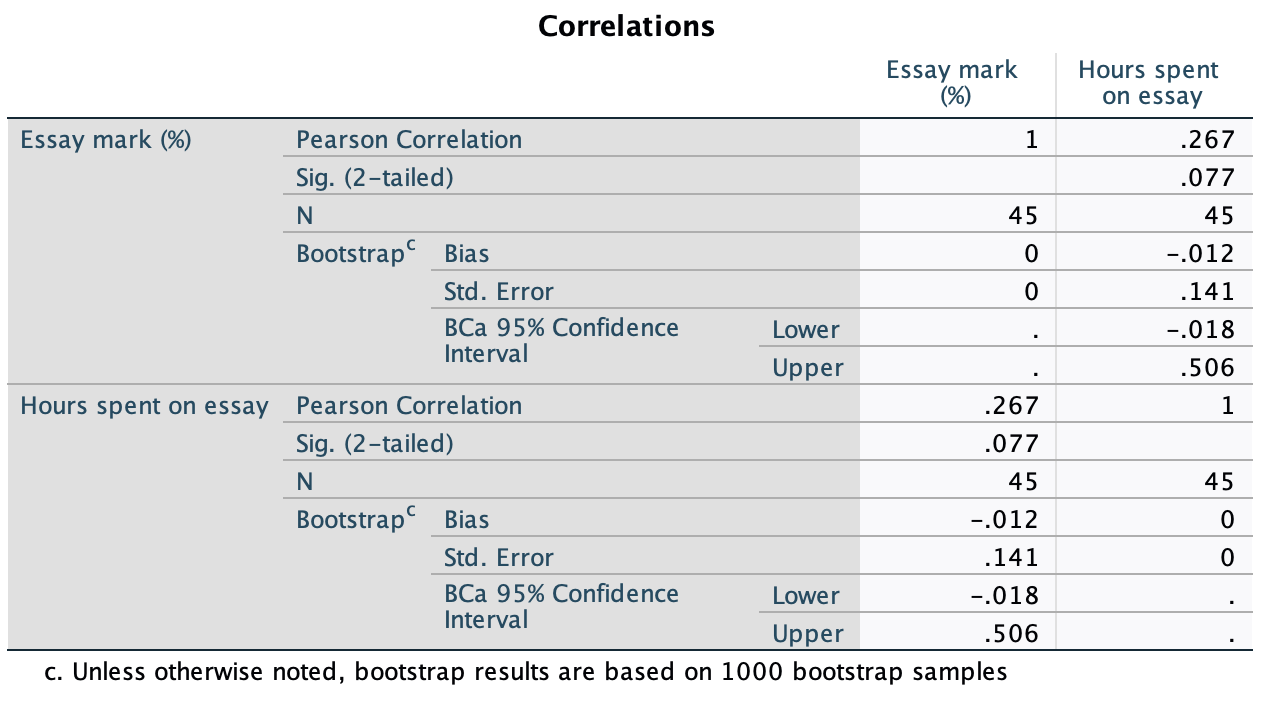
The second part of the question asks us to do the same analysis but when the percentages are recoded into degree classifications. The degree classifications are ordinal data (not interval): they are ordered categories. So we shouldn’t use Pearson’s test statistic, but Spearman’s and Kendall’s ones instead (Figure 122).
In both cases the correlation is non-significant. There was no significant relationship between degree grade classification for an essay and the time spent doing it, \(\rho\) = 0.19, p = 0.204, and \(\tau\) = –0.16, p = 0.178. Note that the direction of the relationship has reversed. This has happened because the essay marks were recoded as 1 (first), 2 (upper second), 3 (lower second), and 4 (third), so high grades were represented by low numbers. This example illustrates one of the benefits of not taking continuous data (like percentages) and transforming them into categorical data: when you do, you lose information and often statistical power!
Task 8.2
Using the
notebook.savdata from Chapter 3, quantify the relationship between the participant’s gender and arousal.
Gender identity is a categorical variable with two categories, therefore, we need to quantify this relationship using a point-biserial correlation. I used a two-tailed test because one-tailed tests should never really be used. I have also asked for the bootstrapped confidence intervals as they are robust. Figure 123 shows that there was no significant relationship between biological sex and arousal because the p-value is larger than 0.05 and the bootstrapped confidence intervals cross zero, \(r_\text{pb}\) = –0.20, 95% BCa CI [–0.50, 0.13], p = 0.266.
Task 8.3
Using the notebook data again, quantify the relationship between the film watched and arousal.
There was a significant relationship between the film watched and arousal, \(r_\text{pb}\) = –0.87, 95% BCa CI [–0.91, –0.81], p < 0.001. Looking in the data at how the groups were coded, you should see that The Notebook had a code of 1, and the documentary about notebooks had a code of 2, therefore the negative coefficient reflects the fact that as film goes up (changes from 1 to 2) arousal goes down. Put another way, as the film changes from The Notebook to a documentary about notebooks, arousal decreases. So The Notebook gave rise to the greater arousal levels.
Task 8.4
As a statistics lecturer I am interested in the factors that determine whether a student will do well on a statistics course. Imagine I took 25 students and looked at their grades for my statistics course at the end of their first year at university: first, upper second, lower second and third class (see Task 1). I also asked these students what grade they got in their high school maths exams. In the UK GCSEs are school exams taken at age 16 that are graded A, B, C, D, E or F (an A grade is the best). The data for this study are in the file
grades.sav. To what degree does GCSE maths grade correlate with first-year statistics grade?
Let’s look at these variables. In the UK, GCSEs are school exams taken at age 16 that are graded A, B, C, D, E or F. These grades are categories that have an order of importance (an A grade is better than all of the lower grades). In the UK, a university student can get a first-class mark, an upper second, a lower second, a third, a pass or a fail. These grades are categories, but they have an order to them (an upper second is better than a lower second). When you have categories like these that can be ordered in a meaningful way, the data are said to be ordinal. The data are not interval, because a first-class degree encompasses a 30% range (70–100%), whereas an upper second only covers a 10% range (60–70%). When data have been measured at only the ordinal level they are said to be non-parametric and Pearson’s correlation is not appropriate. Therefore, the Spearman correlation coefficient is used.
In the file, the scores are in two columns: one labelled stats and one labelled gcse. Each of the categories described above has been coded with a numeric value. In both cases, the highest grade (first class or A grade) has been coded with the value 1, with subsequent categories being labelled 2, 3 and so on. Note that for each numeric code I have provided a value label (just like we did for coding variables).
In the question I predicted that better grades in GCSE maths would correlate with better degree grades for my statistics course. This hypothesis is directional and so a one-tailed test could be selected; however, in the chapter I advised against one-tailed tests so I have done two-tailed.
The SPSS output (Figure 125) shows the Spearman correlation on the variables stats and gcse. The output shows a matrix giving the correlation coefficient between the two variables (0.455), underneath is the significance value of this coefficient (0.022) and then the sample size (25). [Note: it is good to check that the value of N corresponds to the number of observations that were made. If it doesn’t then data may have been excluded for some reason.]
I also requested the bootstrapped confidence intervals (–0.014, 0.738). The significance value for this correlation coefficient is less than 0.05; therefore, it can be concluded that there is a significant relationship between a student’s grade in GCSE maths and their degree grade for their statistics course. However, the bootstrapped confidence interval crosses zero, suggesting (under the usual assumptions) that the effect in the population could be zero. It is worth remembering that if we were to rerun the analysis we would get different results for the bootstrap confidence interval. In fact, I have rerun the analysis (Figure 126), and the resulting output is below. You can see that this time the confidence interval does not cross zero (0.079, 0.705), which suggests that there is likely to be a positive effect in the population (as GCSE grades improve, there is a corresponding improvement in degree grades for statistics). The p-value is only just significant (0.022), although the correlation coefficient is fairly large (0.455). This situation demonstrates that it is important to replicate studies.
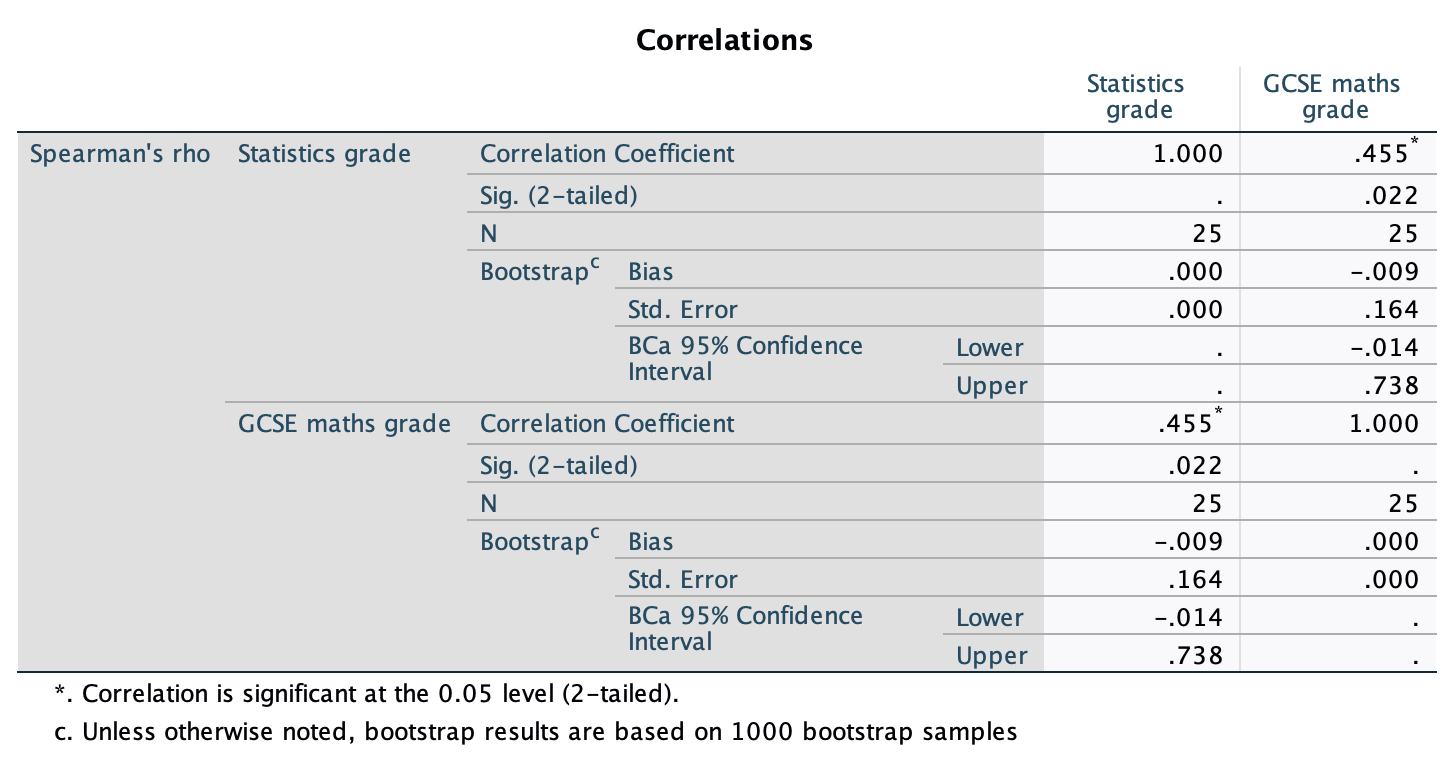
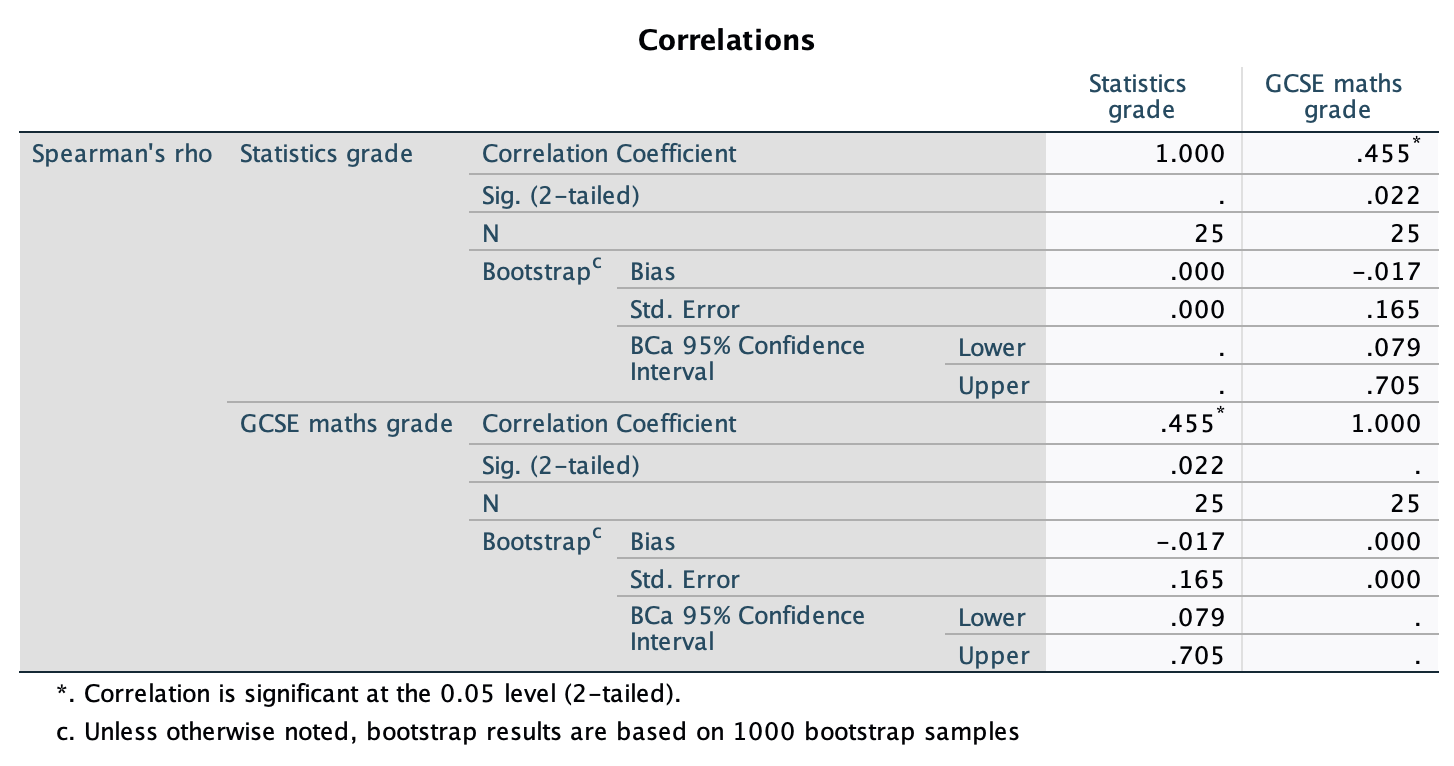
We could also look at Kendall’s correlation. The output (Figure 127) is much the same as for Spearman’s correlation. The value of Kendall’s coefficient is less than Spearman’s (it has decreased from 0.455 to 0.354), but it is still statistically significant (because the p-value of 0.029 is less than 0.05). The bootstrapped confidence intervals do not cross zero (0.042, 0.632) suggesting that there is likely to be a positive relationship in the population. We cannot assume that the GCSE grades caused the degree students to do better in their statistics course.
We could report these results as follows:
Task 8.5
In Figure 2.3 (in the book) we saw some data relating to people’s ratings of dishonest acts and the likeableness of the perpetrator (for a full description see Jane Superbrain Box 2.1). Compute the Spearman correlation between ratings of dishonesty and likeableness of the perpetrator. The data are in
honesty_lab.sav.
Figure 128 shows that the relationship between ratings of dishonesty and likeableness of the perpetrator was significant because the p-value is less than 0.05 (p = 0.000) and the bootstrapped confidence intervals do not cross zero (0.770, 0.895). The value of Spearman’s correlation coefficient is quite large and positive (0.844), indicating a large positive effect: the more likeable the perpetrator was, the more positively their dishonest acts were viewed.
Task 8.6
: In Chapter 4 (Task 6) we looked at data from people who had fish or cats as pets and measured their life satisfaction and, also, how much they like animals (
pets.sav). Is there a significant correlation between life satisfaction and the type of animal the person had as a pet?
pet is a categorical variable with two categories (fish or cat). Therefore, we need to look at this relationship using a point-biserial correlation. I also asked for 95% confidence intervals (given the small sample, we might have been better off with bootstrap confidence intervals, but I want to mix things up). I used a two-tailed test because one-tailed tests should never really be used (see book chapter for more explanation). Figure 129 shows that there was a significant relationship between type of pet and life satisfaction because the oberved p-value is less than the criterion of 0.05 and the confidence intervals do not cross zero, \(r_\text{pb}\) = 0.63, BCa CI [0.25, 0.83], p = 0.003. Looking at how the groups were coded, fish had a code of 1 and cat had a code of 2, therefore this result reflects the fact that as the type of pet changes (from fish to cat) life satisfaction goes up. Put another way, as having a cat as a pet was associated with greater life satisfaction.
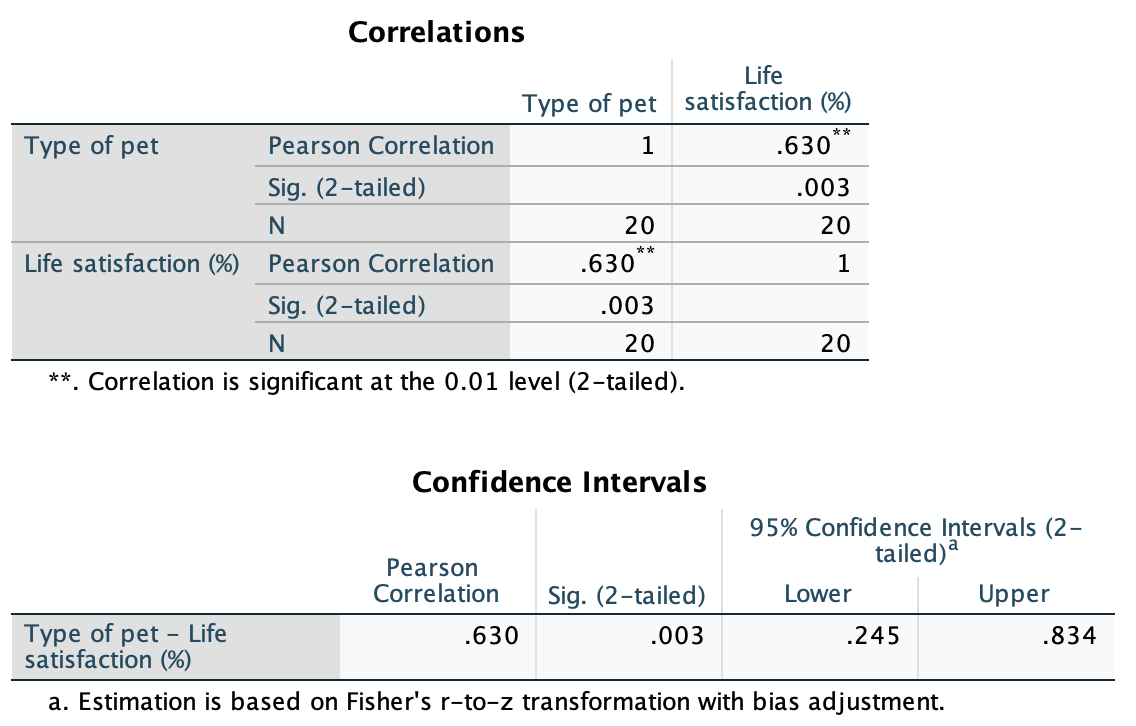
Task 8.7
Repeat the analysis above taking account of animal liking when computing the correlation between life satisfaction and the type of animal the person had as a pet.
We can conduct a partial correlation between life satisfaction and the pet the person has while ‘adjusting’ for the effect of liking animals. The output (Figure 130) for the partial correlation is a matrix of correlations for the variables pet and life_satisfaction but adjusting for the love of animals. Note that the top and bottom of the table contain identical values, so we can ignore one half of the table. First, notice that the partial correlation between pet and life_satisfaction is 0.701, which is greater than the correlation when the effect of animal liking is not adjusted for (r = 0.630). The correlation has become more statistically significant (its p-value has decreased from 0.003 to < 0.001) and the confidence interval [0.47, 0.87] still doesn’t contain zero. In terms of variance, the value of \(R^2\) for the partial correlation is 0.491, which means that type of pet shares 49.1% of the variance in life satisfaction (compared to 39.7% when when not adjusting for love of animals). Running this analysis has shown us that the relationship between the type of pet and life satisfaction is not due to how much the owners love animals.
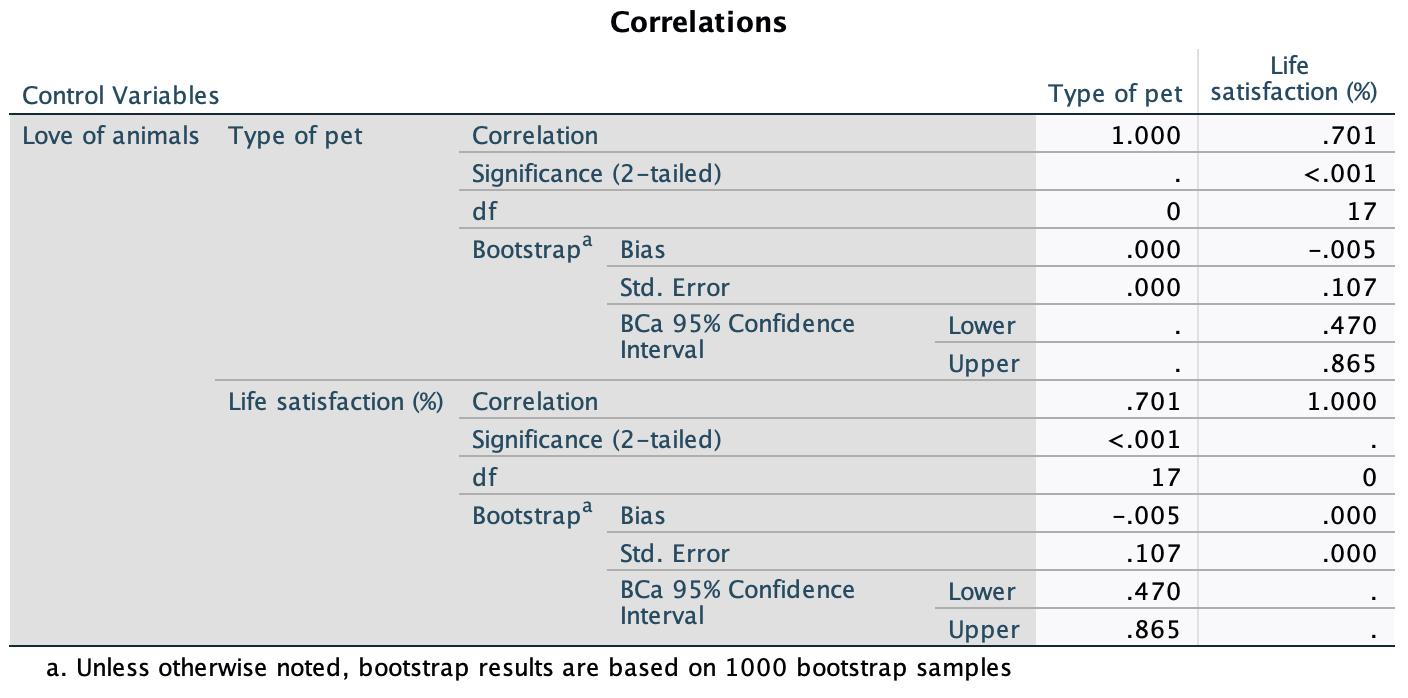
Task 8.8
In Chapter 4 (Task 7) we looked at data based on findings that the number of cups of tea drunk was related to cognitive functioning (Feng et al., 2010). The data are in the file
tea_15.sav. What is the correlation between tea drinking and cognitive functioning? Is there a significant effect?
Because the numbers of cups of tea and cognitive function are both interval variables, we can conduct a Pearson’s correlation coefficient. If we request bootstrapped confidence intervals then we don’t need to worry about checking whether the data are normal because they are robust. I chose a two-tailed test because it is never really appropriate to conduct a one-tailed test (see the book chapter). Figure 131 indicates that the relationship between number of cups of tea drunk per day and cognitive function was not significant. We can tell this because our p-value is greater than 0.05 (the typical criterion), and the bootstrapped confidence intervals cross zero, indicating that under the usual assumption that this sample is one of the 95% that generated a confidence interval containing the true value, the effect in the population could be zero (i.e. no effect). Pearson’s r = 0.078, 95% BCa CI [–0.38, 0.52], p = 0.783.
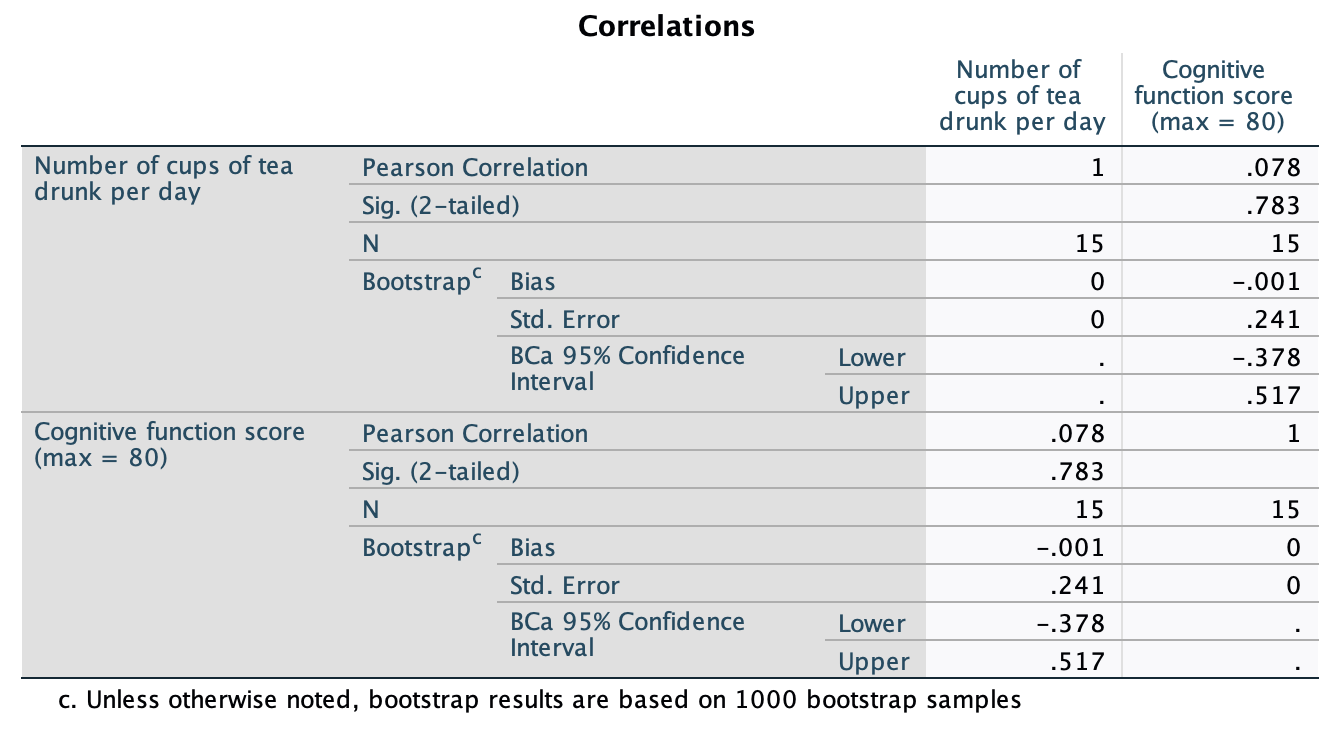
Task 8.9
The research in the previous task was replicated but in a larger sample (N = 716), which is the same as the sample size in Feng et al.’s research (
tea_716.sav). Conduct a correlation between tea drinking and cognitive functioning. Compare the correlation coefficient and significance in this large sample, with the previous task. What statistical point do the results illustrate?
Figure 132 shows that although the value of Pearson’s r has not changed, it is still very small (0.078), the relationship between the number of cups of tea drunk per day and cognitive function is now just significant (p = 0.038) if you use the common criterion of \(\alpha = 0.05\), and the confidence intervals no longer cross zero (0.001, 0.156). (Although note that the lower confidence interval is very close to zero, suggesting that under the usual assumptions the effect in the population could be very close to zero.)
This example indicates one of the downfalls of significance testing; you can get significant results when you have large sample sizes even if the effect is very small. Basically, whether you get a significant result or not is at the mercy of the sample size.
Task 8.10
In Chapter 6 we looked at hygiene scores over three days of a rock music festival (
download.sav). Using Spearman’s correlation, were hygiene scores on day 1 of the festival significantly correlated with those on day 3?
The hygiene scores on day 1 of the festival correlated significantly with hygiene scores on day 3 (Figure 133). The value of Spearman’s correlation coefficient is 0.344, which is a positive value suggesting that the smellier you are on day 1, the smellier you will be on day 3, \(r_\text{s}\) = 0.34, 95% BCa CI [0.16, 0.50], p < 0.001.
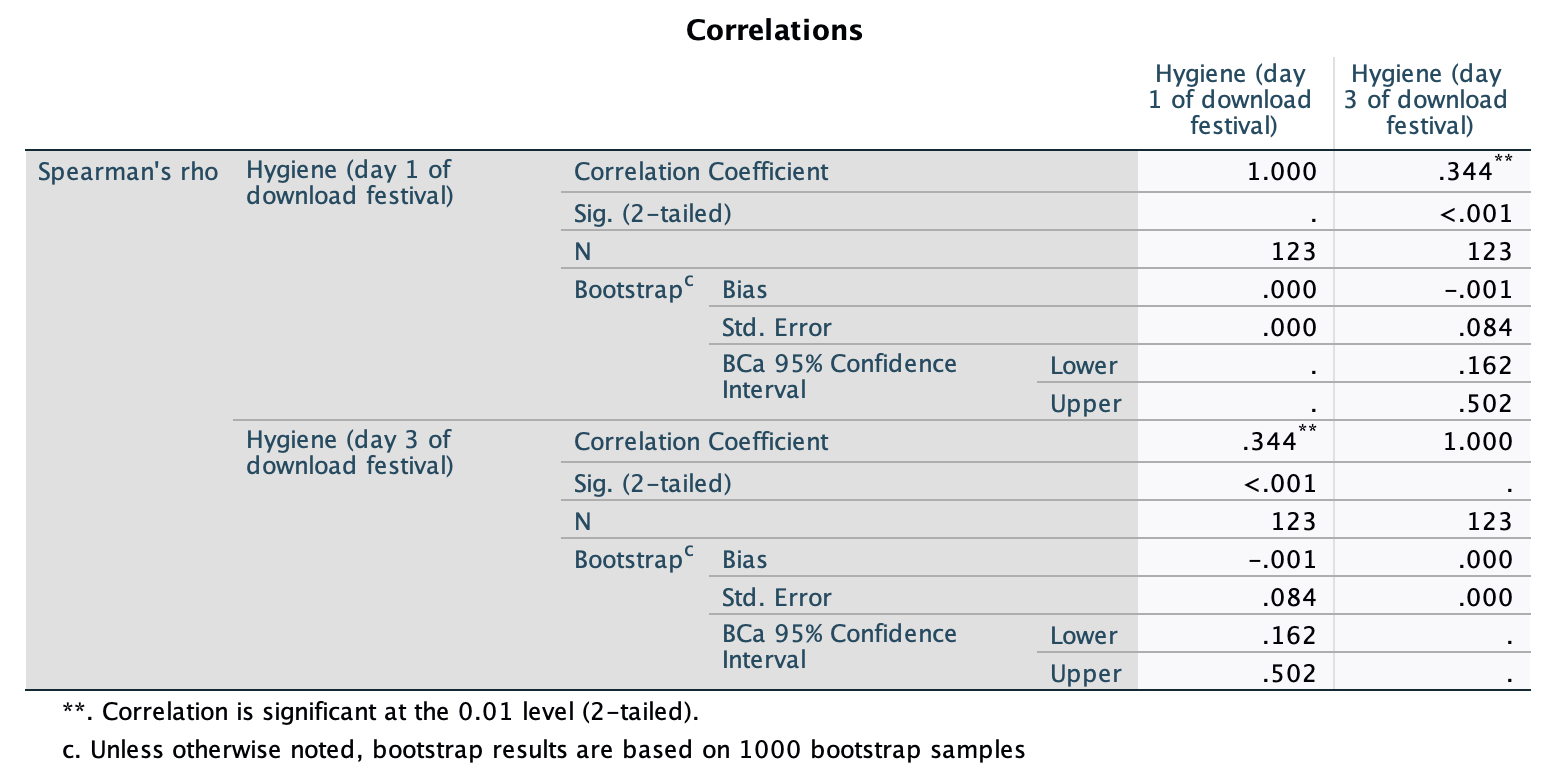
Task 8.11
Using the data in shopping.sav (Chapter 4, Task 5), find out if there is a significant relationship between the time spent shopping and the distance covered.
The variables time and distance are both interval. Therefore, we can conduct a Pearson’s correlation. I chose a two-tailed test because it is never really appropriate to conduct a one-tailed test (see the book chapter). Figure 134 indicates that there was a significant positive relationship between time spent shopping and distance covered using the common criterion of \(\alpha = 0.05\). We can tell that the relationship was significant because the p-value is smaller than 0.05. More important, the robust confidence intervals do not cross zero suggesting (under the usual assumptions) that the effect in the population is unlikely to be zero. Also, our value for Pearson’s r is very large (0.83) indicating a large effect. Pearson’s r = 0.83, 95% BCa CI [0.59, 0.96], p = 0.003.
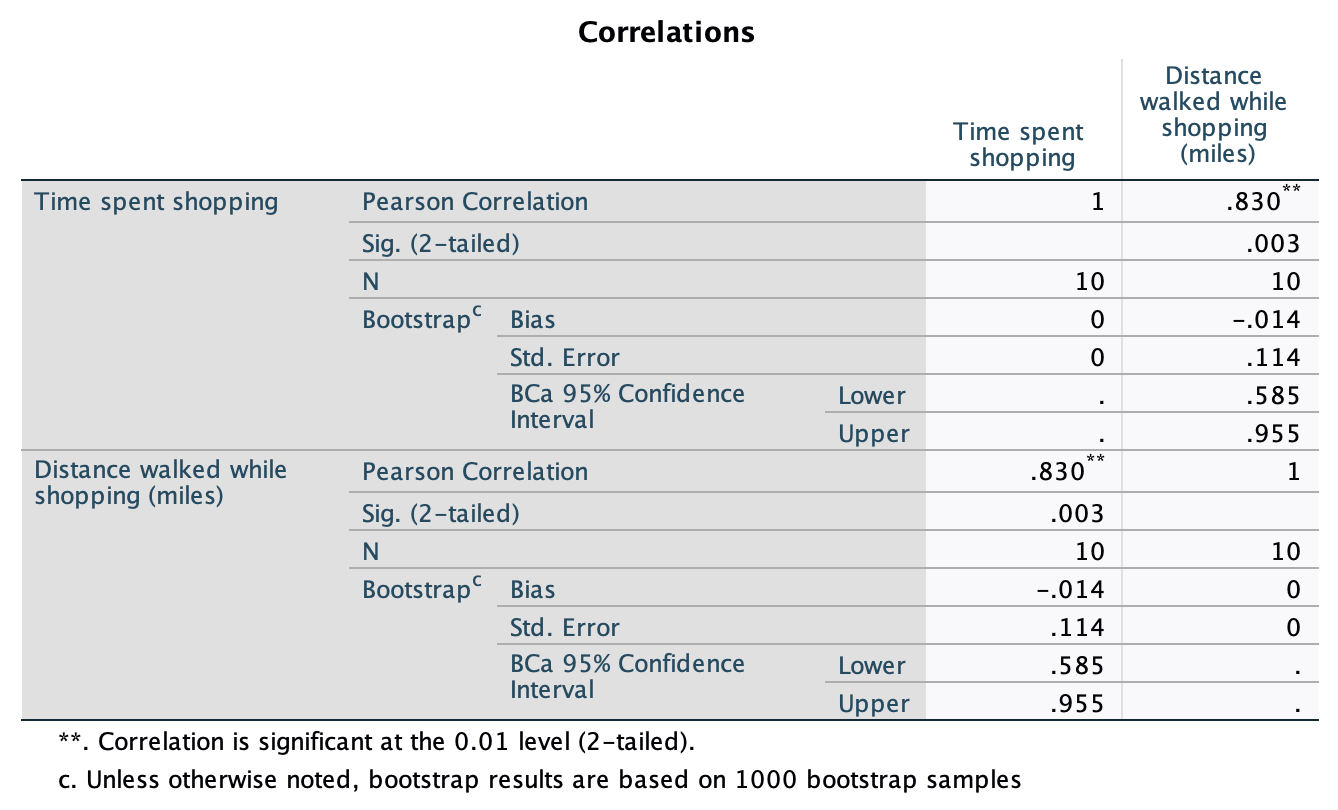
Task 8.12
What effect does accounting for the participant’s sex have on the relationship between the time spent shopping and the distance covered?
To answer this question, we need to conduct a partial correlation between the time spent shopping (interval variable) and the distance covered (interval variable) while ‘adjusting’ for the effect of sex (dichotomous variable). The partial correlation between time and distance is 0.820, which is slightly smaller than the correlation when we don’t adjust for sex (r = 0.830). The correlation has become slightly less statistically significant (its p-value has increased from 0.003 to 0.007). In terms of variance, the value of \(R^2\) for the partial correlation is 0.672, which means that time spent shopping now shares 67.2% of the variance in distance covered when shopping (compared to 68.9% when not adjusted for sex). Running this analysis has shown us that time spent shopping alone explains a large portion of the variation in distance covered.
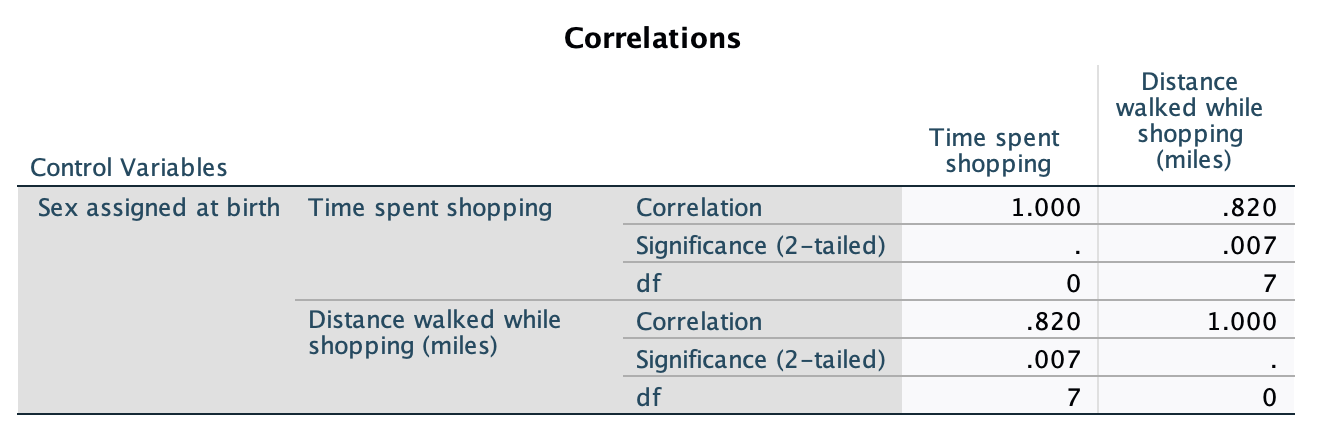
Chapter 9
Task 9.1
In Chapter 8 (Task 9) we looked at data based on findings that the number of cups of tea drunk was related to cognitive functioning (Feng et al., 2010). Using a linear model that predicts cognitive functioning from tea drinking, what would cognitive functioning be if someone drank 10 cups of tea? Is there a significant effect? (
tea_716.sav)
The basic output from SPSS Statistics is as follows:
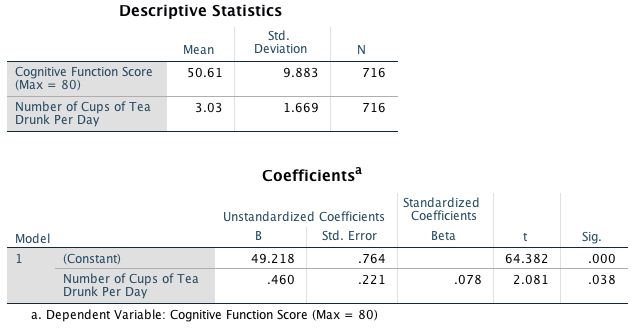
Looking at the output below, we can see that we have a model that significantly improves our ability to predict cognitive functioning. The positive standardized beta value (0.078) indicates a positive relationship between number of cups of tea drunk per day and level of cognitive functioning, in that the more tea drunk, the higher your level of cognitive functioning. We can then use the model to predict level of cognitive functioning after drinking 10 cups of tea per day. The first stage is to define the model by replacing the b-values in the equation below with the values from the Coefficients output. In addition, we can replace the X and Y with the variable names so that the model becomes:
\[ \begin{aligned} \widehat{\text{Cognitive functioning}}_i &= b_0 + b_1 \text{Tea drinking}_i \\ \ &= 49.22 +(0.460 \times \text{Tea drinking}_i) \end{aligned} \]
We can predict cognitive functioning, by replacing Tea drinking in the equation with the value 10:
\[ \begin{aligned} \widehat{\text{Cognitive functioning}}_i &= 49.22 +(0.460 \times \text{Tea drinking}_i) \\ &= 49.22 +(0.460 \times 10) \\ &= 53.82 \end{aligned} \]
Therefore, if you drank 10 cups of tea per day, your predicted level of cognitive functioning would be 53.82.
Task 9.2
Estimate a linear model for the
pubs.savdata in Jane Superbrain Box 9.1 predictingmortalityfrom the number ofpubs. Try repeating the analysis but bootstrapping the confidence intervals.
Looking at the output (Figure 137), we can see that the number of pubs significantly predicts mortality, t(6) = 3.33, p = 0.016. The positive beta value (0.806) indicates a positive relationship between number of pubs and death rate in that, the more pubs in an area, the higher the rate of mortality (as we would expect). The value of \(R^2\) tells us that number of pubs accounts for 64.9% of the variance in mortality rate – that’s over half!
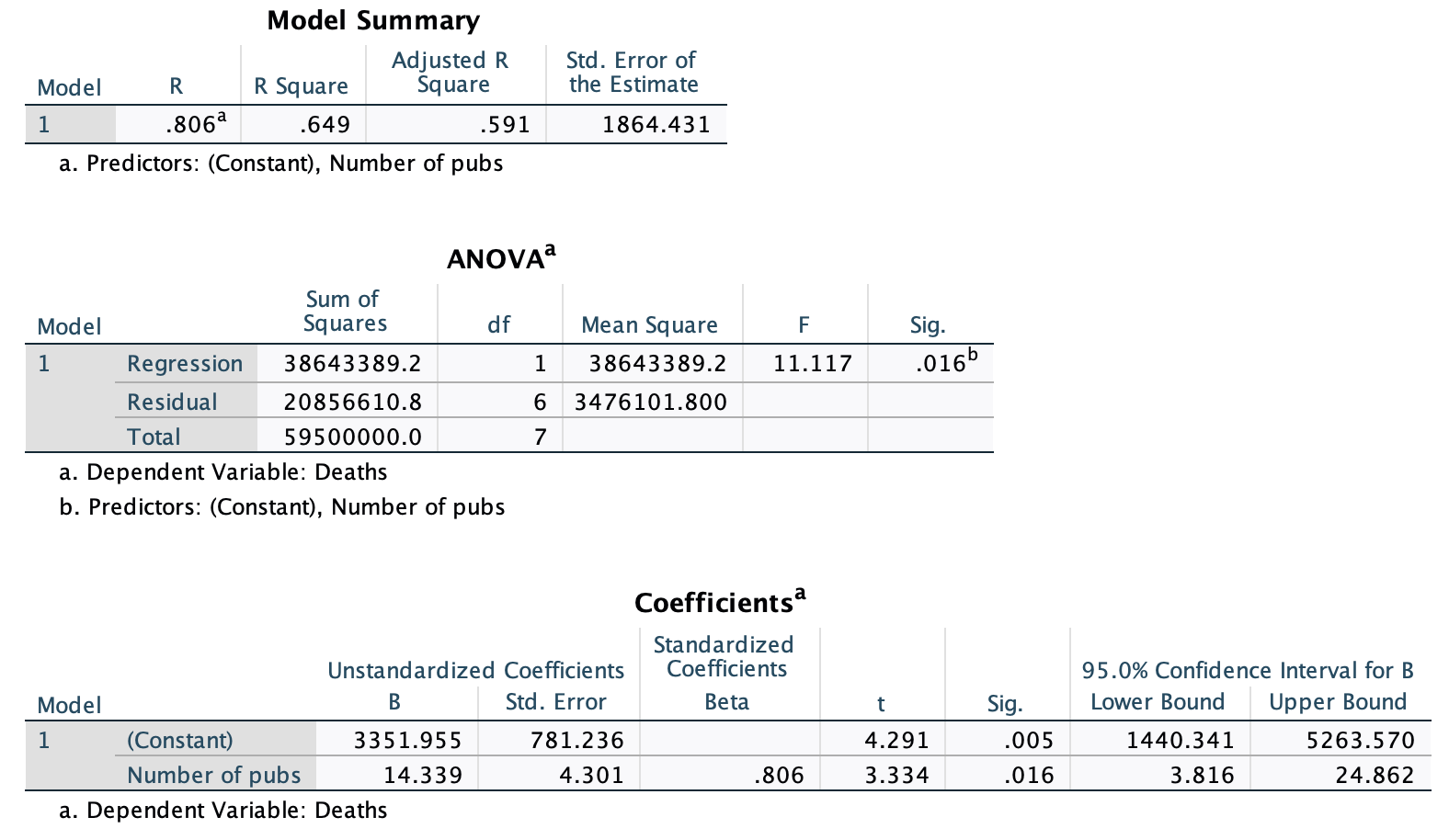
To get the bootstrap confidence intervals to work, you’ll need to select Percentile bootstrap (not BCa). Figure 138 shows that the bootstrapped confidence intervals are both positive values – they do not cross zero (10.76, 100.00). Assuming this interval is one of the 95% that contain the population value then it appears that there is a positive and non-zero relationship between number of pubs in an area and its mortality rate.
Task 9.3
In Jane Superbrain Box 2.1 we encountered data (
honesty_lab.sav) relating to people’s ratings of dishonest acts and the likeableness of the perpetrator. Run a linear model with bootstrapping to predict ratings ofdishonestyfrom thelikeablenessof the perpetrator.
Figure 139 shows that the likeableness of the perpetrator significantly predicts ratings of dishonest acts, t(98) = 14.80, p < 0.001. The positive standardized beta value (0.83) indicates a positive relationship between likeableness of the perpetrator and ratings of dishonesty, in that, the more likeable the perpetrator, the more positively their dishonest acts were viewed (remember that dishonest acts were measured on a scale from 0 = appalling behaviour to 10 = it’s OK really). The value of \(R^2\) tells us that likeableness of the perpetrator accounts for 69.1% of the variance in the rating of dishonesty, which is over half.
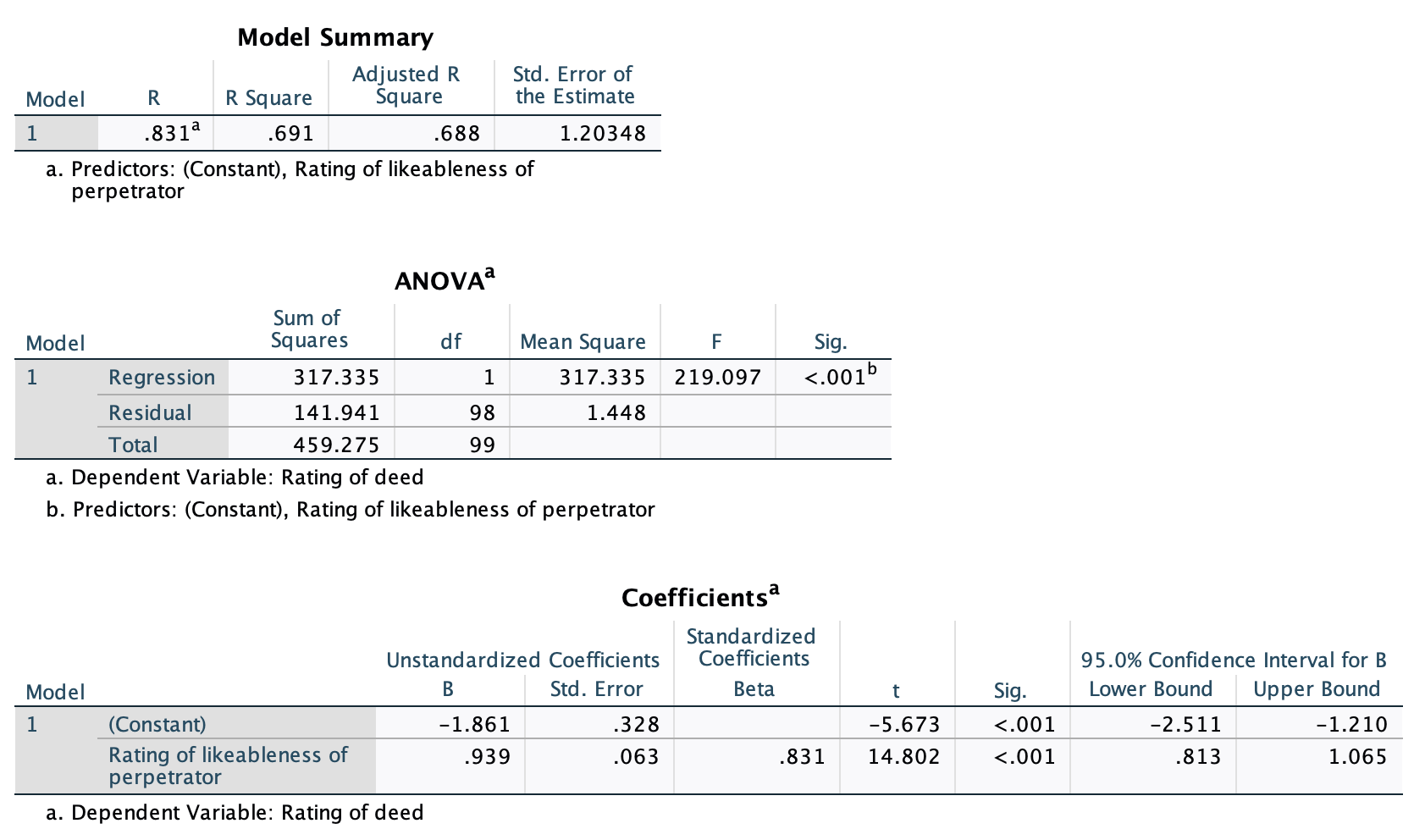
Figure 140 shows that the bootstrapped confidence intervals do not cross zero (0.81, 1.07). Assuming sample is one of the 95% that produces an interval containing the population value it appears that there is a non-zero relationship between the likeableness of the perpetrator and ratings of dishonest acts.
Task 9.4
A fashion student was interested in factors that predicted the salaries of catwalk models. She collected data from 231 models (
supermodel.sav). For each model she asked them their salary per day (salary), their age (age), their length of experience as models (years), and their industry status as a model as reflected in their percentile position rated by a panel of experts (status). Use a linear model to see which variables predict a model’s salary. How valid is the model?
The model
To begin with, a sample size of 231 with three predictors seems reasonable because this would easily detect medium to large effects (see the diagram in the chapter). Overall, the model is a significant fit to the data, F(3, 227) = 17.07, p < .001 (Figure 141). The adjusted \(R^2\) (0.17) suggests that 17% of the variance in salaries can be explained by the model when adjusting for the number of predictors.
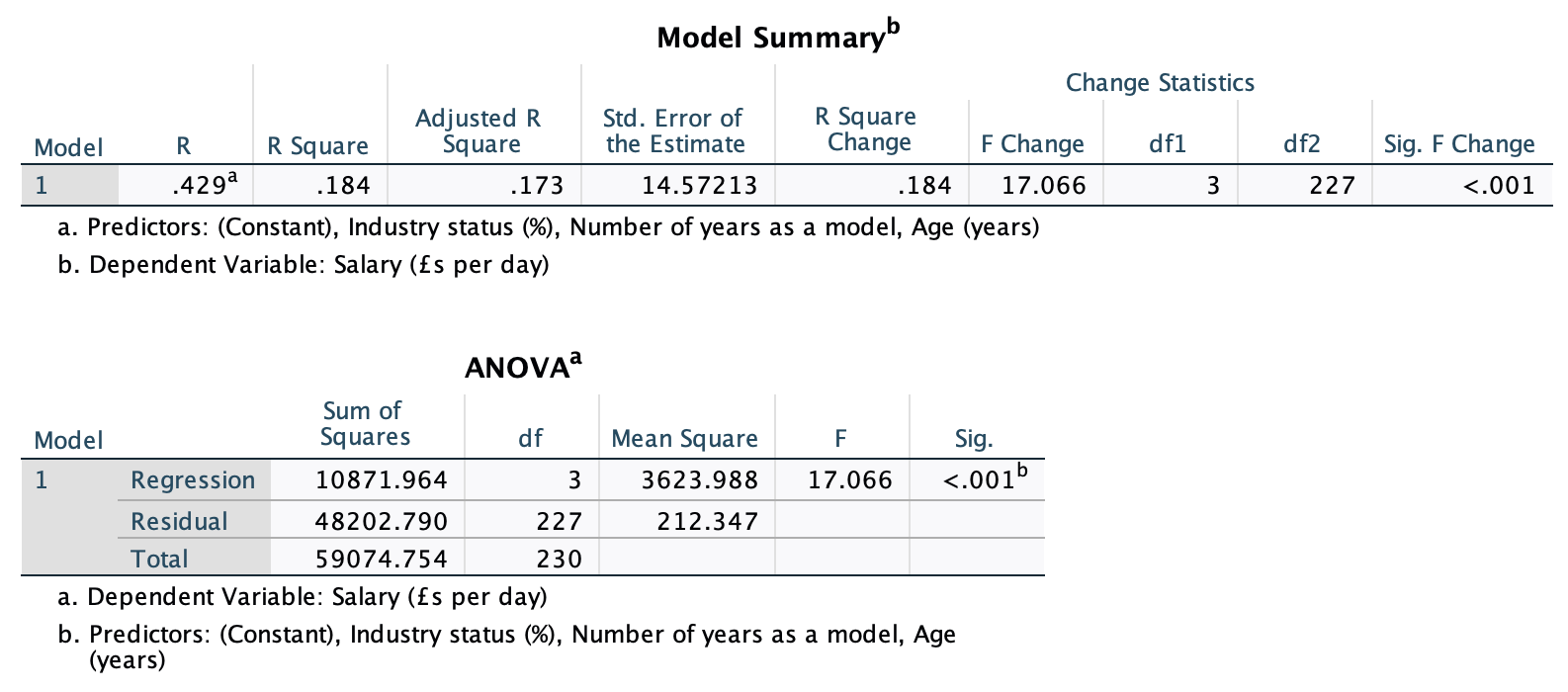
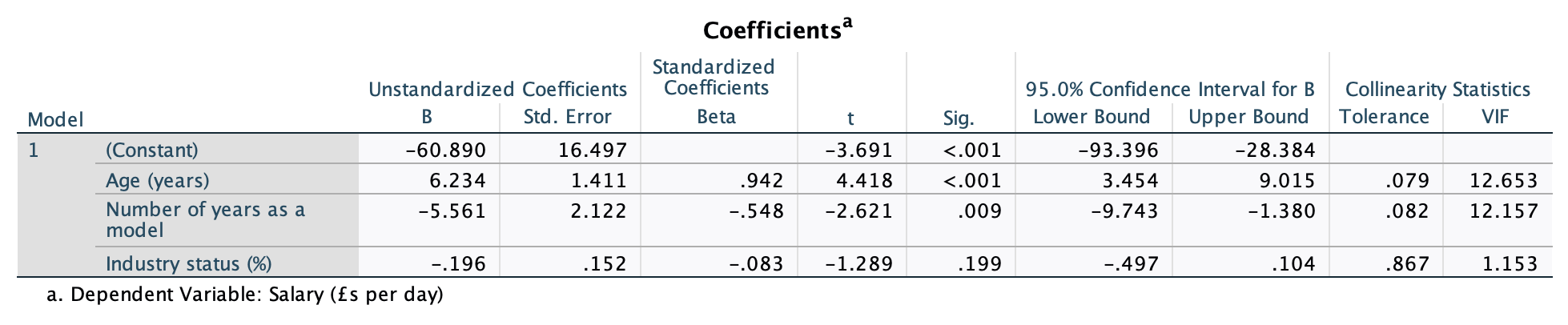
In terms of the individual predictors we could report (Figure 142):
The next part of the question asks whether this model is valid.
- Residuals (Figure 143): There are six cases that have a standardized residual greater than 3, and two of these are fairly substantial (case 5 and 135). We have 5.19% of cases with standardized residuals above 2, so that’s as we expect, but 3% of cases with residuals above 2.5 (we’d expect only 1%), which indicates possible outliers.
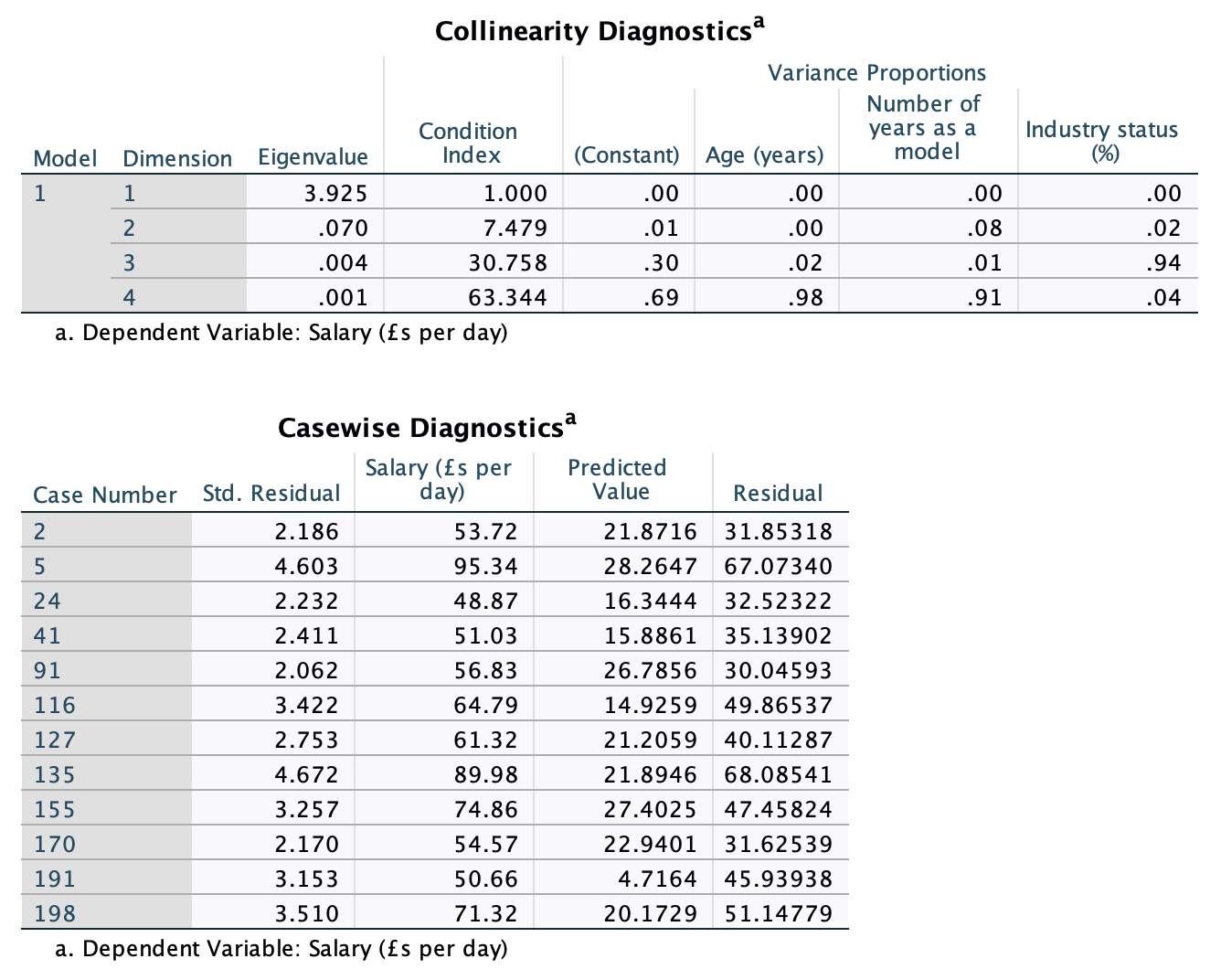
- Normality of errors: The histogram reveals a skewed distribution (Figure 144), indicating that the normality of errors assumption has been broken. The normal P–P plot (Figure 145) verifies this because the dashed line deviates considerably from the straight line (which indicates what you’d get from normally distributed errors).
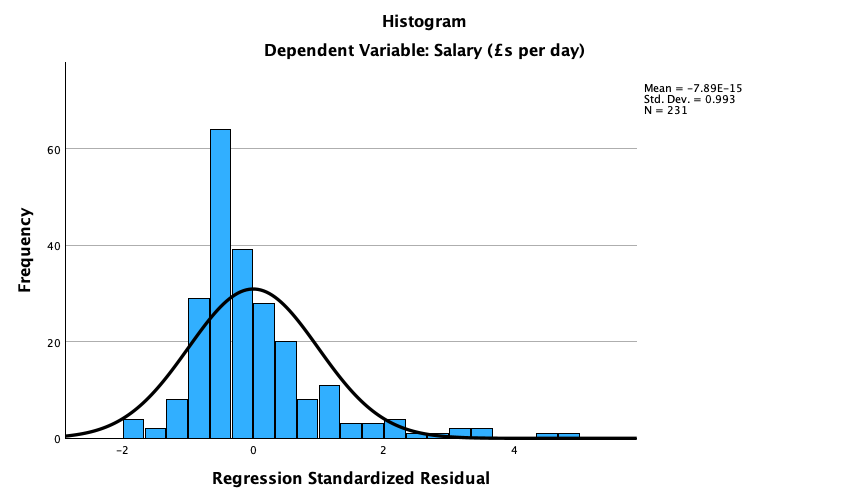
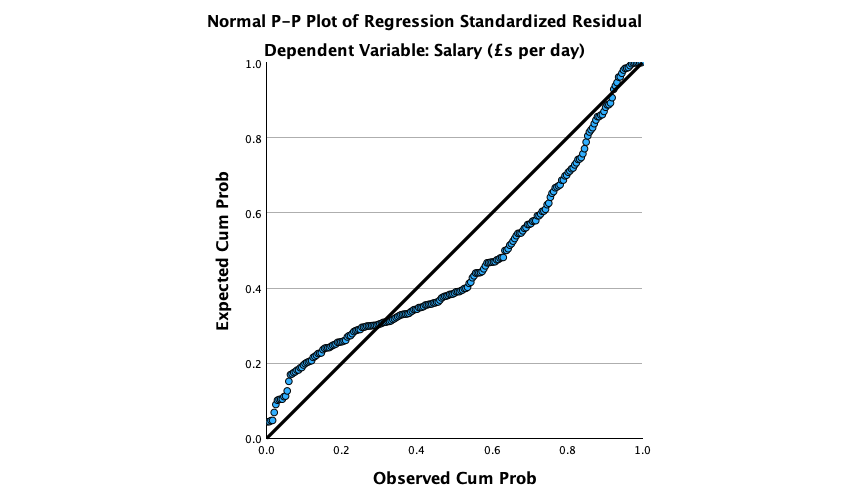
-
Homoscedasticity and independence of errors: The scatterplot of ZPRED vs. ZRESid does not show a random pattern. There is a distinct funnelling, indicating heteroscedasticity (Figure 146). The partial plots (especially the one for
age) also seem to indicate some heteroscedasticity (Figure 147, Figure 148, Figure 149).
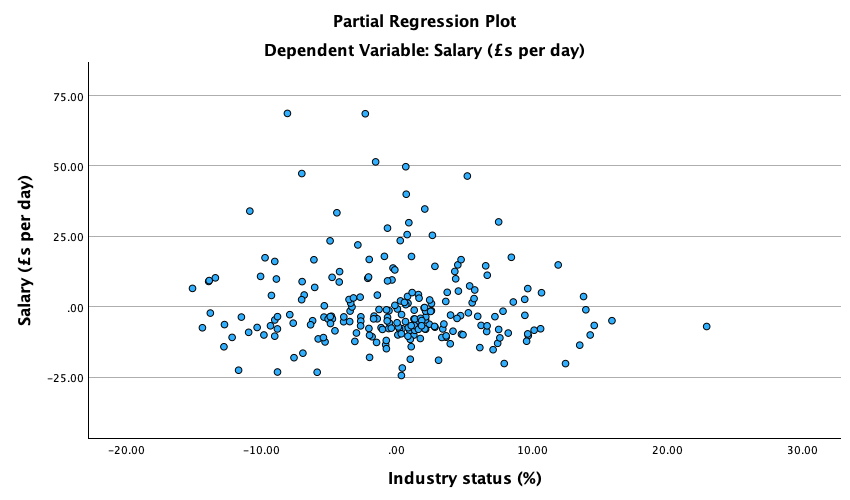
-
Multicollinearity: For the
ageandyearsvariables, VIF values are above 10 (or alternatively, tolerance values are all well below 0.2), indicating multicollinearity in the data (Figure 142). Looking at the variance proportions for these variables (Figure 143) it seems like they are expressing similar information. In fact, the correlation between these two variables is around .9! So, these two variables are measuring very similar things. Of course, this makes perfect sense because the older a model is, the more years she would’ve spent modelling! So, it was fairly stupid to measure both of these things! This also explains the weird result that the number of years spent modelling negatively predicted salary (i.e. more experience = less salary!): in fact if you do a simple regression withyearsas the only predictor of salary you’ll find it has the expected positive relationship. This hopefully demonstrates why multicollinearity can bias the regression model.
All in all, several assumptions have not been met and so this model is probably fairly unreliable.
Task 9.5
A study was carried out to explore the relationship between aggression and several potential predicting factors in 666 children who had an older sibling. Variables measured were
parenting_style(high score = bad parenting practices),computer_games(high score = more time spent playing computer games),television(high score = more time spent watching television),diet(high score = the child has a good diet low in harmful additives), andsibling_aggression(high score = more aggression seen in their older sibling). Past research indicated that parenting style and sibling aggression were good predictors of the level of aggression in the younger child. All other variables were treated in an exploratory fashion. Analyse them with a linear model (child_aggression.sav).
We need to conduct this analysis hierarchically, entering parenting style and sibling aggression in the first step (forced entry) as in Figure 150. The remaining variables are entered in a second step (stepwise) as in Figure 151.
The key output is in Figure 152 to Figure 154.
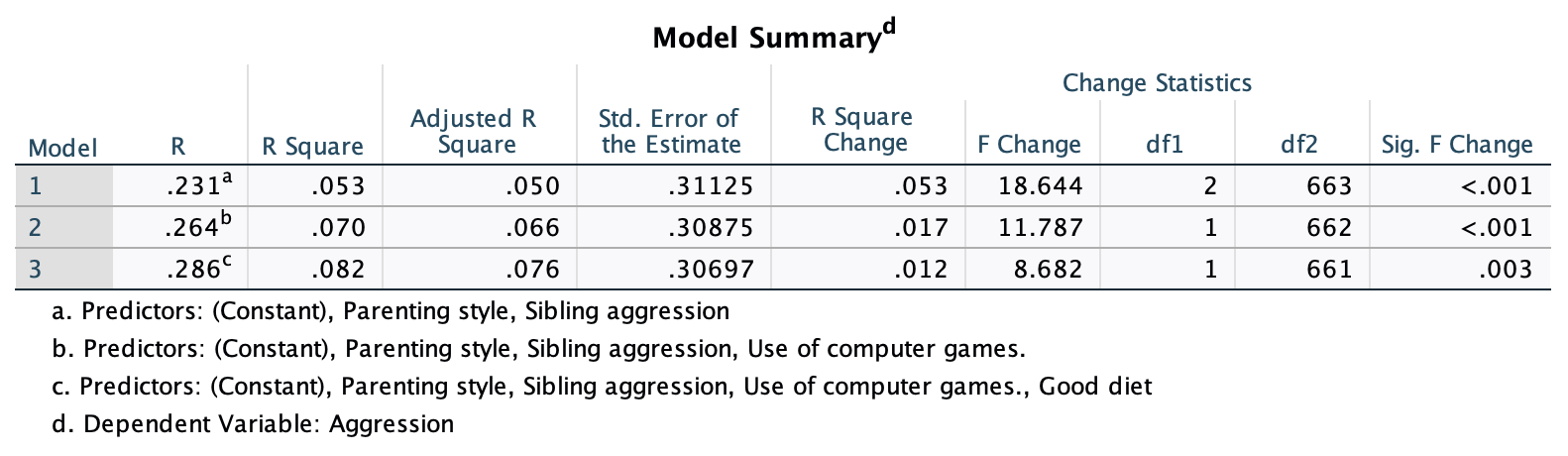
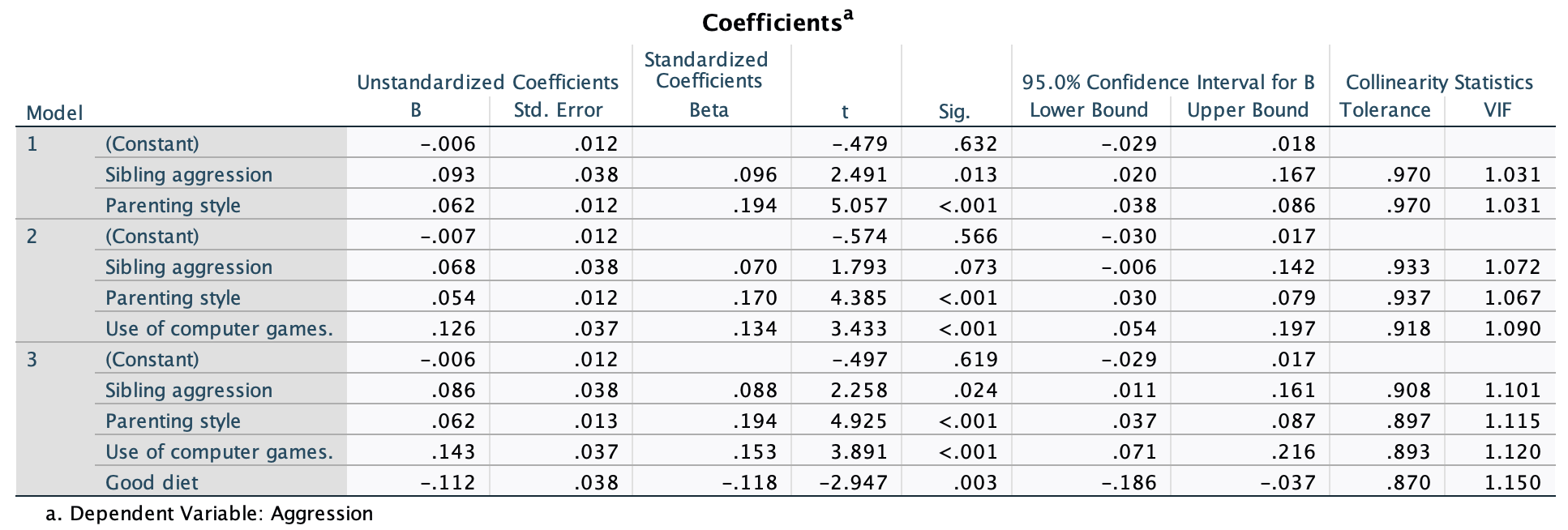
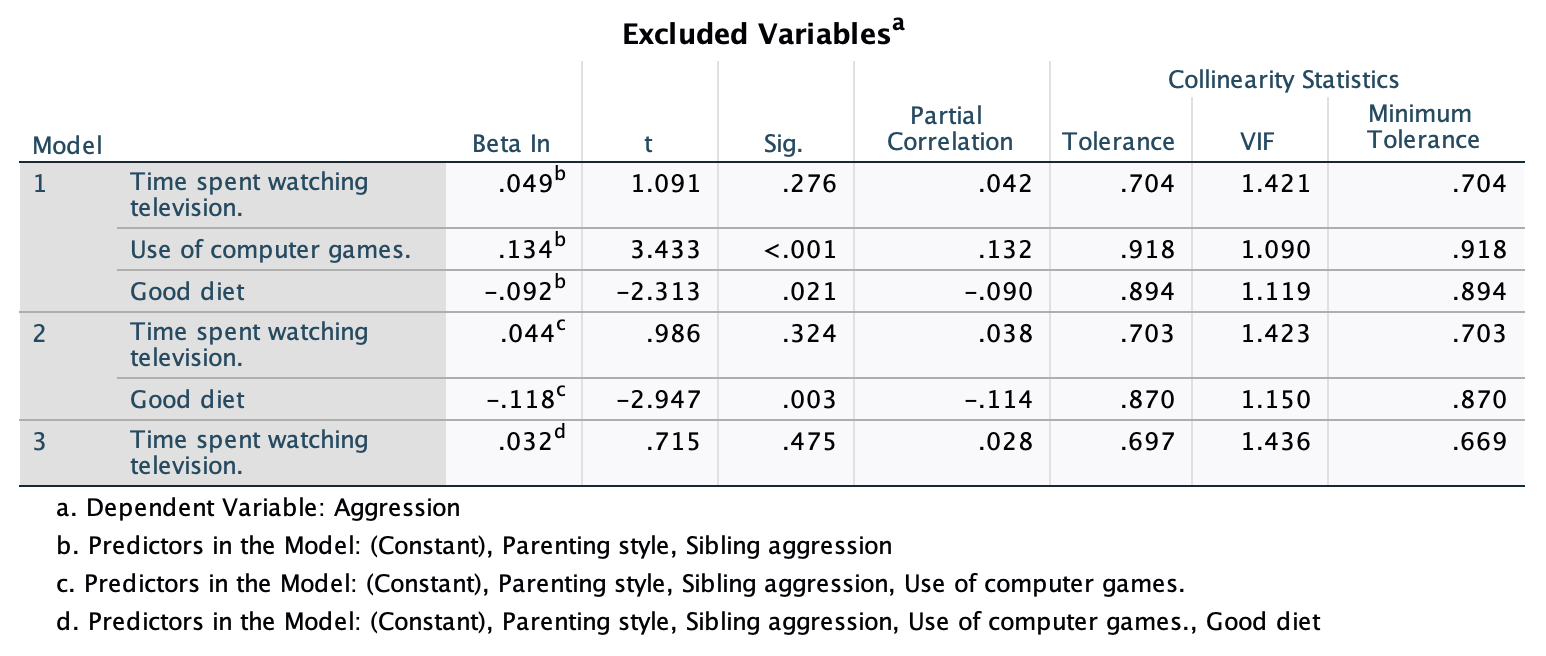
Based on the final model (which is actually all we’re interested in) the following variables predict aggression:
The histogram (Figure 155) and P-P plots (Figure 156) suggest that errors are (approximately) normally distributed. The scatterplot (Figure 157) helps us to assess both homoscedasticity and independence of errors. The scatterplot of ZPRED vs. ZRESid does show a random pattern and so indicates no violation of the independence of errors assumption. Also, the errors on the scatterplot do not funnel out, indicating homoscedasticity of errors, thus no violations of these assumptions.
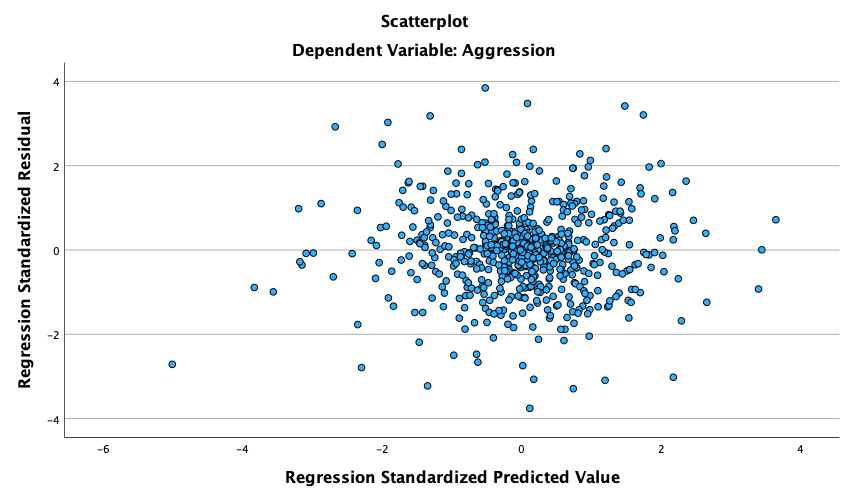
Task 9.6
Repeat the analysis in Labcoat Leni’s Real Research 9.1 using bootstrapping for the confidence intervals. What are the confidence intervals for the regression parameters?
To recap the dialog boxes to run the analysis (see also the Labcoat Leni answers). First, enter grade, age and sex into the model (Figure 158). In a second block, enter NEO_FFI (extroversion) as in Figure 159. In the final block, enter NPQC_R (narcissism) as in Figure 160. We can activate bootstrapping with the options in Figure 161.
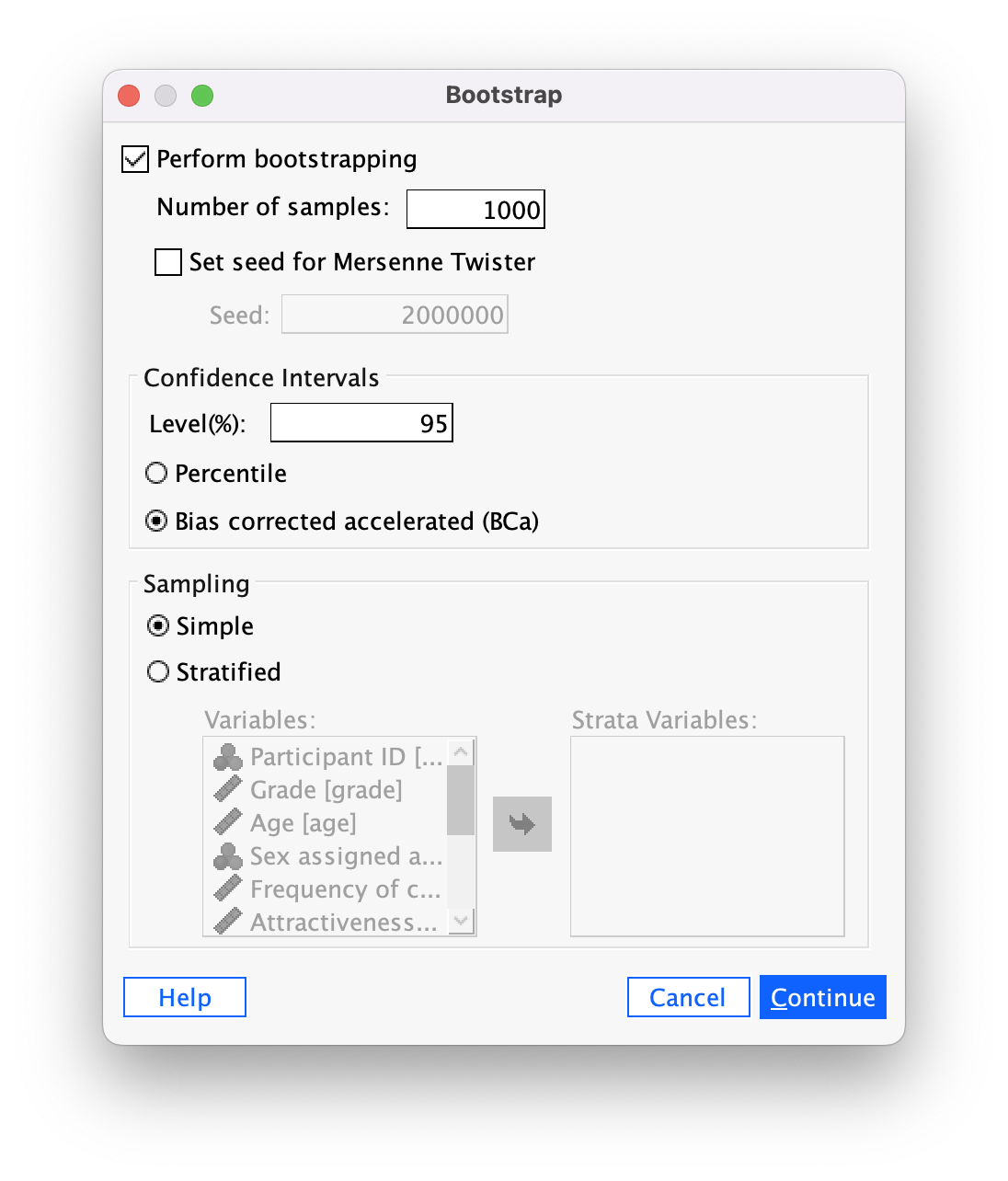
Facebook status update frequency: The main benefit of the bootstrap confidence intervals and significance values is that they do not rely on assumptions of normality or homoscedasticity, so under the usual assumptions they give us an accurate estimate of the true population value of b for each predictor. The bootstrapped confidence intervals in Figure 162 do not affect the conclusions reported in Ong et al. (2011). Ong et al.’s prediction was still supported in that, after controlling for age, grade and gender, narcissism significantly predicted the frequency of Facebook status updates over and above extroversion, b = 0.066 [0.03, 0.10], p = 0.003.
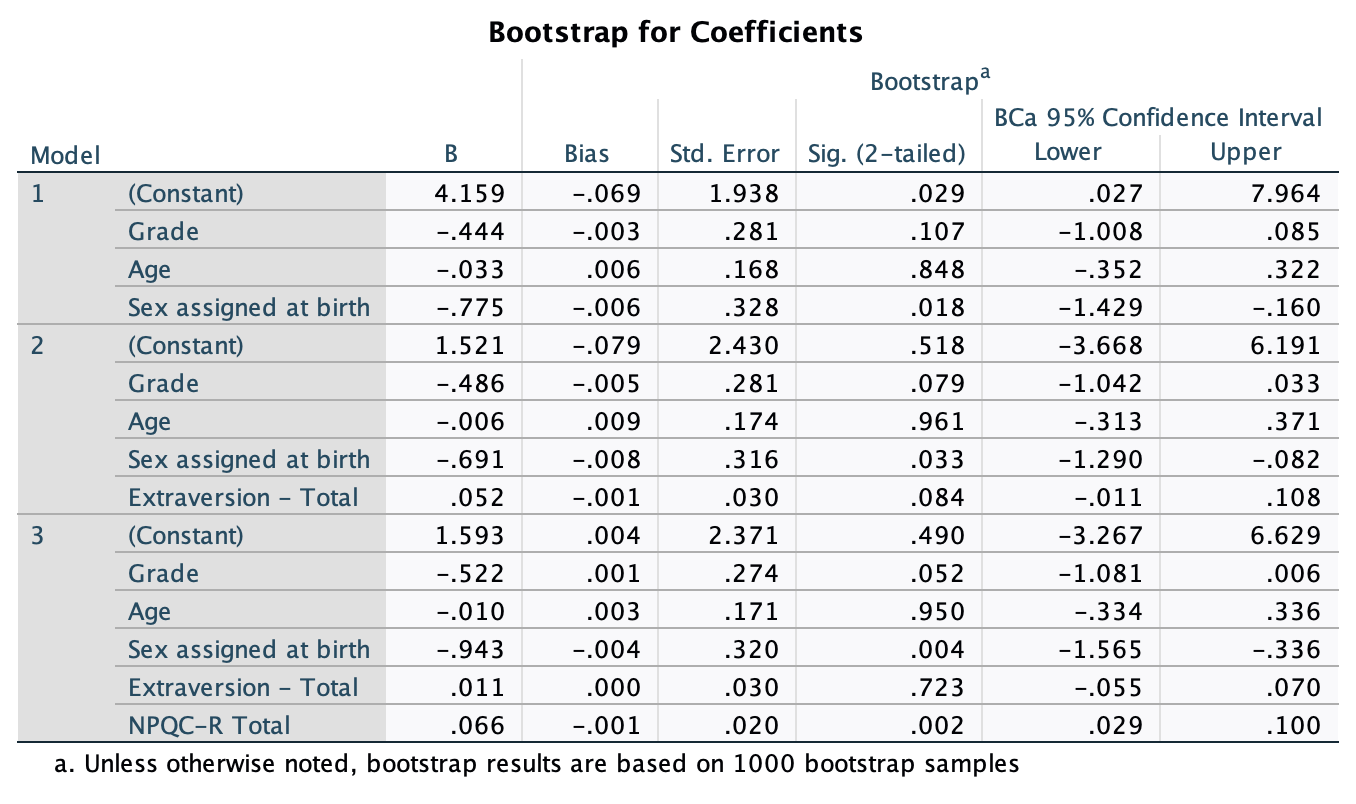
Facebook profile picture rating: Similarly, the bootstrapped confidence intervals for the second regression (Figure 163) are consistent with the conclusions reported in Ong et al. (2011). That is, after adjusting for age, grade and gender, narcissism significantly predicted the Facebook profile picture ratings over and above extroversion, b = 0.173 [0.10, 0.23], p = 0.001.
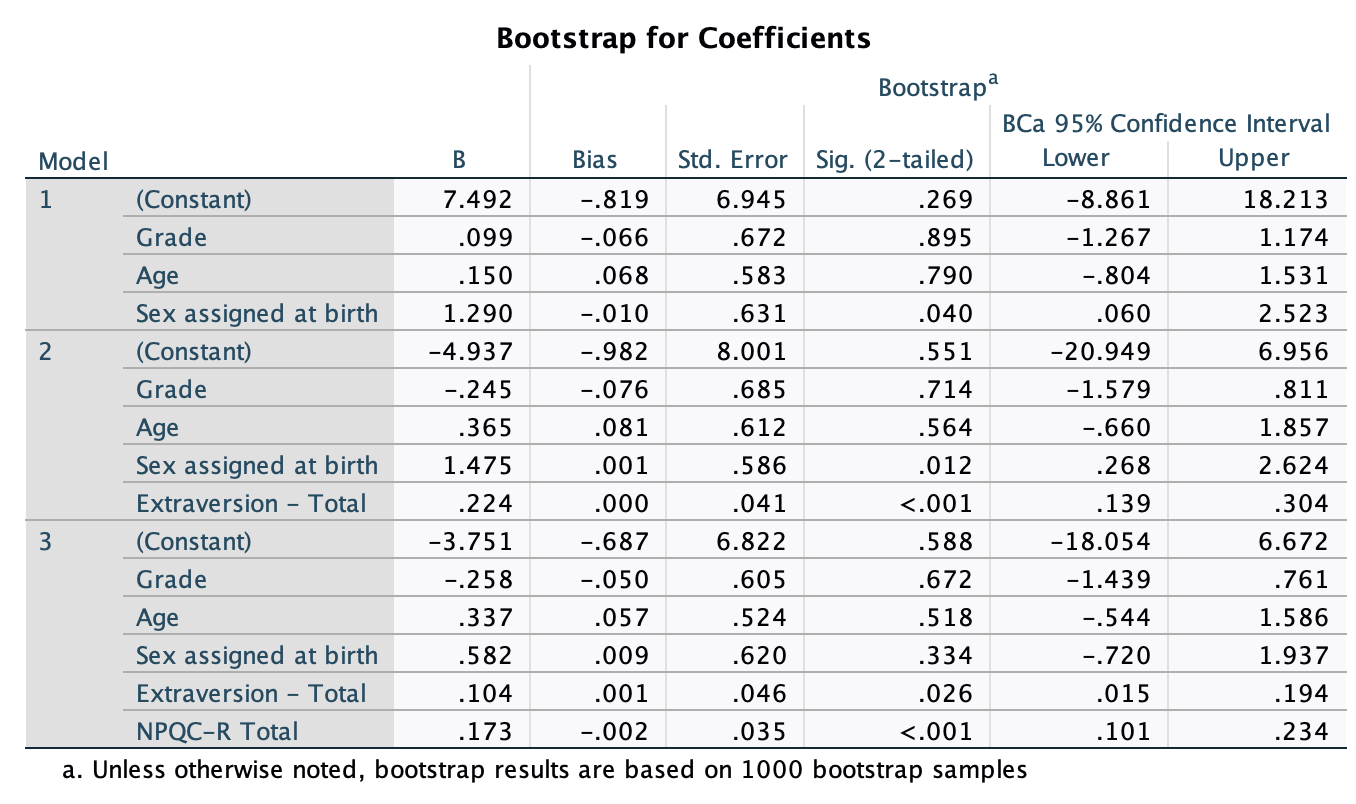
Task 9.7
Coldwell et al. (2006) investigated whether household chaos predicted children’s problem behaviour over and above parenting. From 118 families they recorded the age and gender of the youngest child (
child_ageandchild_gender). They measured dimensions of the child’s perceived relationship with their mum: (1) warmth/enjoyment (child_warmth), and (2) anger/hostility (child_anger). Higher scores indicate more warmth/enjoyment and anger/hostility respectively. They measured the mum’s perceived relationship with her child, resulting in dimensions of positivity (mum_pos) and negativity (mum_neg). Household chaos (chaos) was assessed. The outcome variable was the child’s adjustment (sdq): the higher the score, the more problem behaviour the child was reported to be displaying. Conduct a hierarchical linear model in three steps: (1) enter child age and gender; (2) add the variables measuring parent–child positivity, parent–child negativity, parent–child warmth, parent–child anger; (3) add chaos. Is household chaos predictive of children’s problem behaviour over and above parenting? (coldwell_2006.sav).
To summarize the dialog boxes to run the analysis, first, enter child_age and child_gender into the model and set sdq as the outcome variable (Figure 164). In a new block, add child_anger, child_warmth, mum_pos and mum_neg into the model (Figure 165). In a final block, add chaos to the model (Figure 166). Set some basic options such as those in Figure 167.
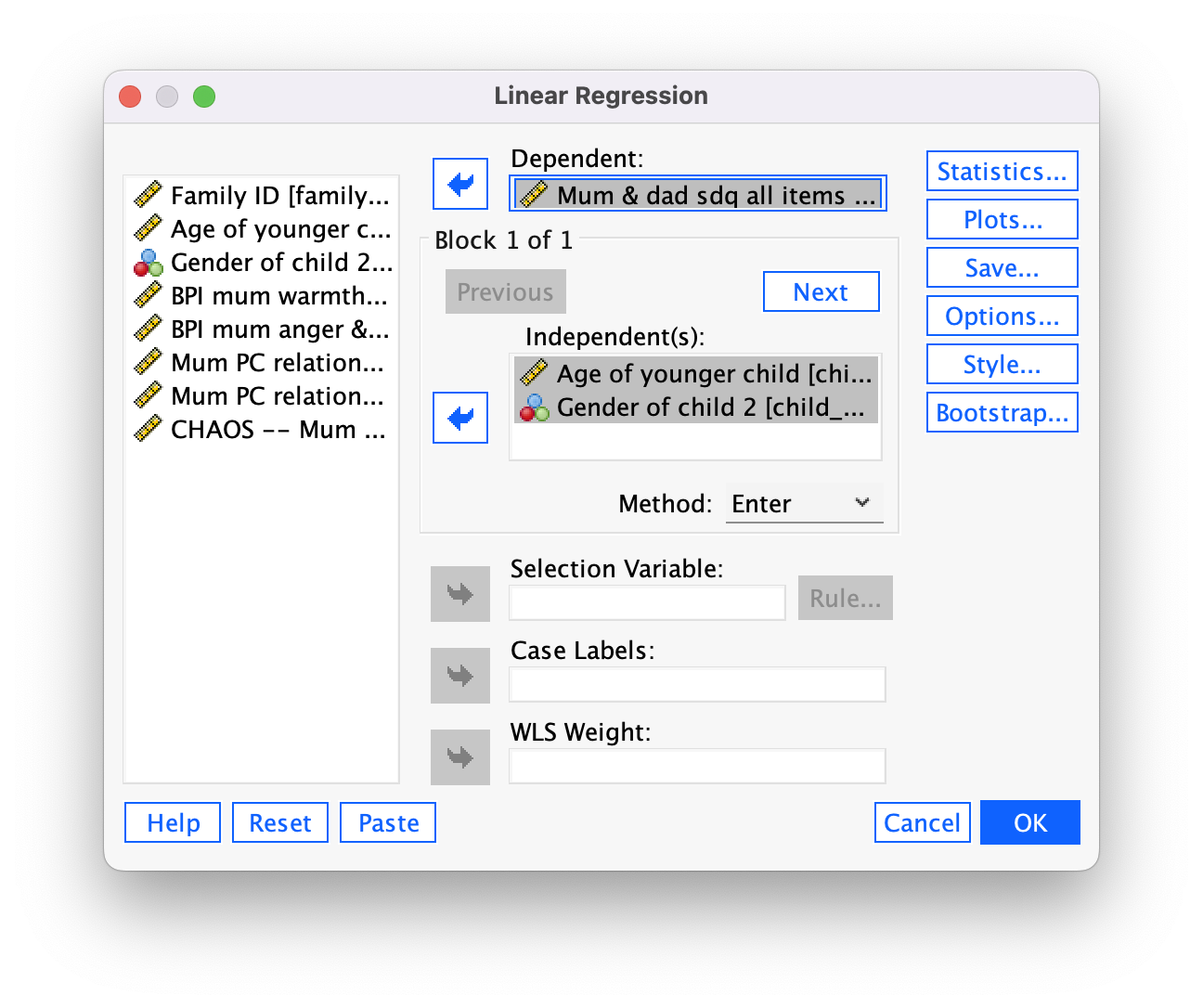

From the output (Figure 170) we can conclude that household chaos significantly predicted younger sibling’s problem behaviour over and above maternal parenting, child age and gender, t(88) = 2.09, p = 0.039. The positive standardized beta value (0.218) indicates that there is a positive relationship between household chaos and child’s problem behaviour. In other words, the higher the level of household chaos, the more problem behaviours the child displayed. The value of \(R^2\) (0.11) tells us that household chaos accounts for 11% of the variance in child problem behaviour (Figure 168).
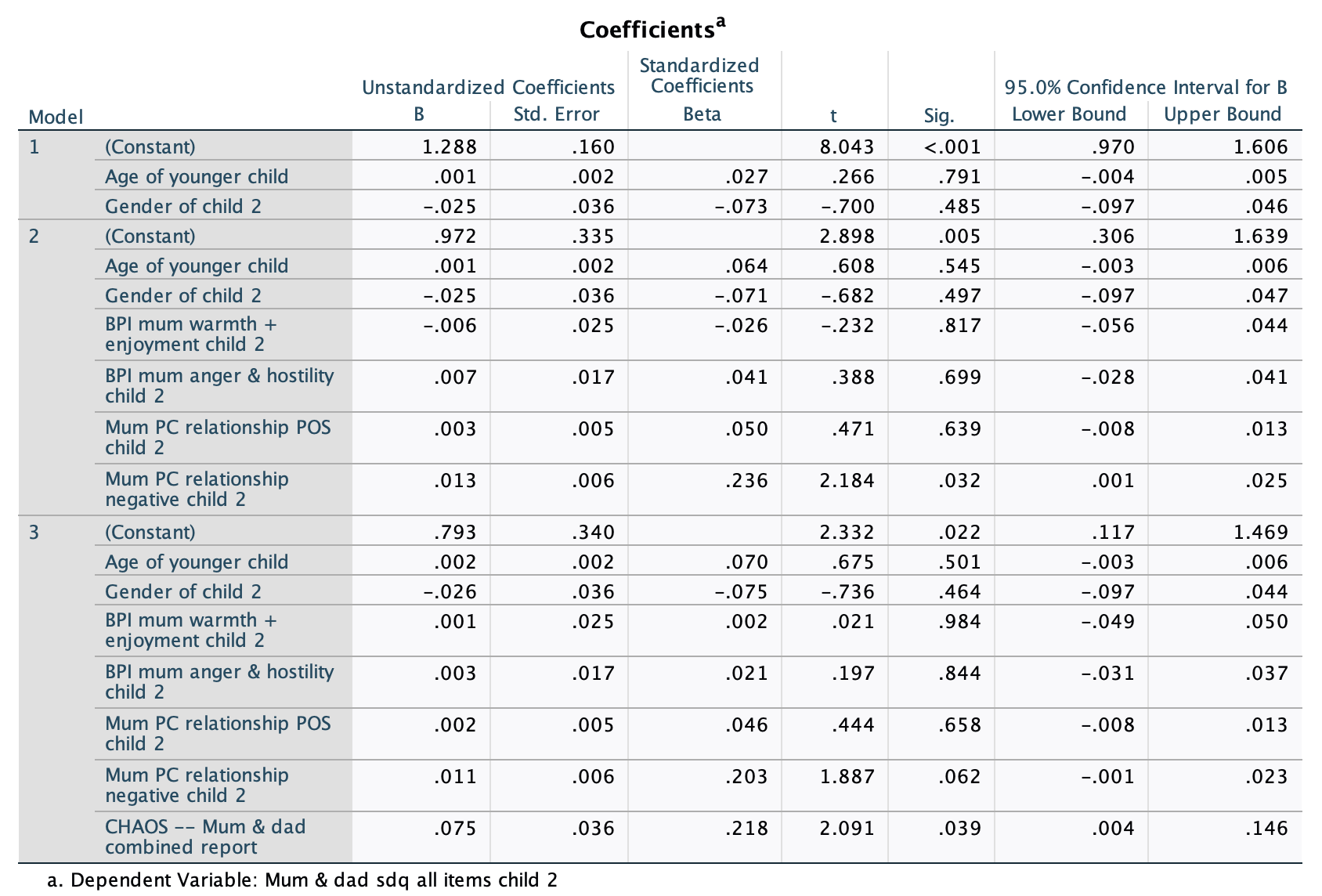
Chapter 10
Task 10.1
Is arachnophobia (fear of spiders) specific to real spiders or will pictures of spiders evoke similar levels of anxiety? Twelve arachnophobes were asked to play with a big hairy tarantula with big fangs and an evil look in its eight eyes and at a different point in time were shown only pictures of the same spider. The participants’ anxiety was measured in each case. Do a t-test to see whether anxiety is higher for real spiders than pictures (
big_hairy_spider.sav).
We have 12 arachnophobes who were exposed to a picture of a spider (picture) and on a separate occasion a real live tarantula (real). Their anxiety was measured in each condition (half of the participants were exposed to the picture before the real spider while the other half were exposed to the real spider first). First, we need to access the main dialog box by selecting Analyze > Compare Means > Paired-Samples T Test …. Once the dialog box is activated, select the pair of variables to be analysed (real and picture) by clicking on one and holding down the Ctrl key (Cmd on a Mac) while clicking on the other. Drag these variables to the box labelled Paired Variables: (or click  ). To run the analysis click
). To run the analysis click  (Figure 171).
(Figure 171).
The resulting output contains three tables. The first contains summary statistics for the two experimental conditions. For each condition we are told the mean, the number of participants (N) and the standard deviation of the sample. In the final column we are told the standard error. The second table contains the Pearson correlation between the two conditions. For these data the experimental conditions yield a fairly large, but not significant, correlation coefficient, r = 0.545, p = 0.067.
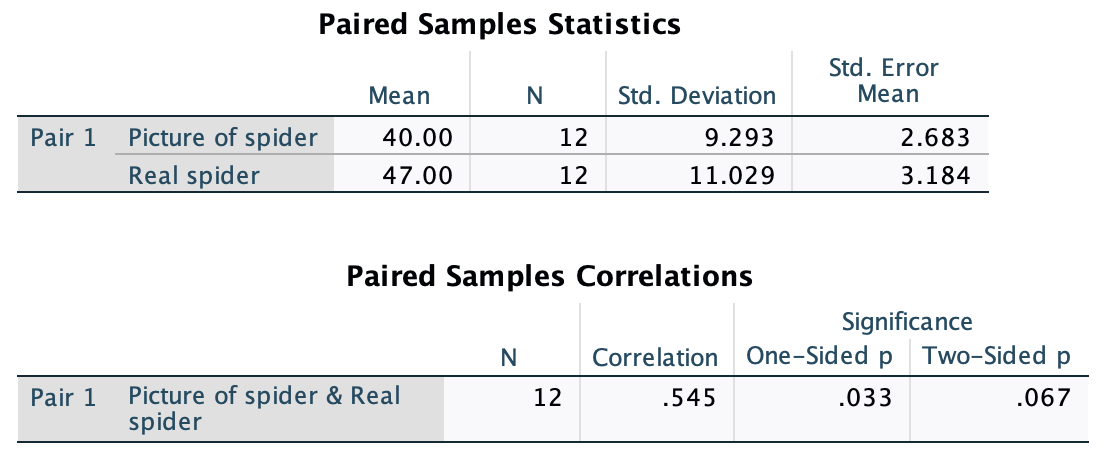
The final table tells us whether the difference between the means of the two conditions was significant;y different from zero. First, the table tells us the mean difference between scores. The table also reports the standard deviation of the differences between the means and, more important, the standard error of the differences between participants’ scores in each condition. The test statistic, t, is calculated by dividing the mean of differences by the standard error of differences (t = −7/2.8311 = −2.47). The size of t is compared against known values (under the null hypothesis) based on the degrees of freedom. When the same participants have been used, the degrees of freedom are the sample size minus 1 (df = N − 1 = 11). SPSS uses the degrees of freedom to calculate the exact probability that a value of t at least as big as the one obtained could occur if the null hypothesis were true (i.e., there was no difference between these means). This probability value is in the column labelled Sig. The two-tailed probability for the spider data is very low (p = 0.031) and significant because 0.031 is smaller than the widely-used criterion of 0.05. The fact that the t-value is a negative number tells us that the first condition (the picture condition) had a smaller mean than the second (the real condition) and so the real spider led to greater anxiety than the picture. Therefore, we can conclude that exposure to a real spider caused significantly more reported anxiety in arachnophobes than exposure to a picture, t(11) = −2.47, p = .031.
Finally, this output contains a 95% confidence interval for the mean difference. Assuming that this sample’s confidence interval is one of the 95 out of 100 that contains the population value, we can say that the true mean difference lies between −13.231 and −0.769. The importance of this interval is that it does not contain zero (i.e., both limits are negative) because this tells us that the true value of the mean difference is unlikely to be zero.

The effect size is given in Figure 174 as \(\hat{d} = -0.63\). Therefore, as well as being statistically significant, this effect is large and probably a substantive finding.
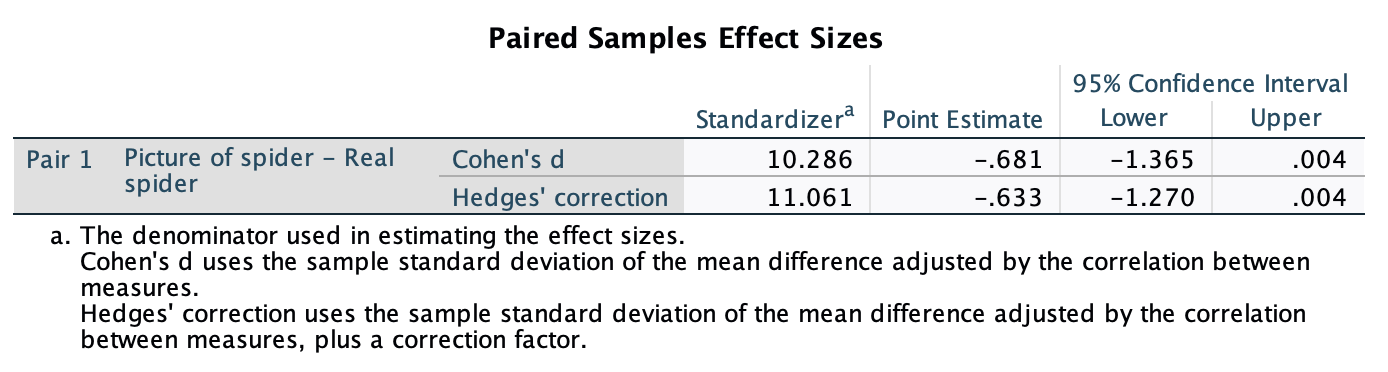
Task 10.2
Plot an error bar plot of the data in Task 1 (remember to adjust for the fact that the data are from a repeated measures design.)
Step 1: Calculate the mean for each participant
To correct the repeated-measures error bars, we need to use the compute command. To begin with, we need to calculate the average anxiety for each participant and so we use the mean function. Access the main compute dialog box by selecting Transform > Compute Variable. Enter the name mean into the box labelled Target Variable and then in the list labelled Function group select Statistical and then in the list labelled Functions and Special Variables select Mean. Transfer this command to the command area by clicking on  . When the command is transferred, it appears in the command area as MEAN(?,?); the question marks should be replaced with variable names (which can be typed manually or transferred from the variables list). So replace the first question mark with the variable
. When the command is transferred, it appears in the command area as MEAN(?,?); the question marks should be replaced with variable names (which can be typed manually or transferred from the variables list). So replace the first question mark with the variable picture and the second one with the variable real. The completed dialog box should look like @#fig-10_2a. Click on  to create this new variable, which will appear as a new column in the data editor.
to create this new variable, which will appear as a new column in the data editor.
Step 2: Calculate the grand mean
Access the descriptives command by selecting Analyze > Descriptive Statistics > Descriptives …. The dialog box shown below should appear. The descriptives command is used to get basic descriptive statistics for variables, and by clicking  a second dialog box is activated. Select the variable
a second dialog box is activated. Select the variable mean from the list and drag it to the box labelled Variable(s) (or click  ). Then use the Options dialog box to specify only the mean (you can leave the default settings as they are, but it is only the mean in which we are interested). If you run this analysis the output should provide you with some self-explanatory descriptive statistics for each of the three variables (assuming you selected all three). You should see that we get the mean of the picture condition, and the mean of the real spider condition, but it’s the final variable we’re interested in: the mean of the picture and spider condition. The mean of this variable is the grand mean, and you can see from the summary table that its value is 43.50. We will use this grand mean in the following calculations.
). Then use the Options dialog box to specify only the mean (you can leave the default settings as they are, but it is only the mean in which we are interested). If you run this analysis the output should provide you with some self-explanatory descriptive statistics for each of the three variables (assuming you selected all three). You should see that we get the mean of the picture condition, and the mean of the real spider condition, but it’s the final variable we’re interested in: the mean of the picture and spider condition. The mean of this variable is the grand mean, and you can see from the summary table that its value is 43.50. We will use this grand mean in the following calculations.
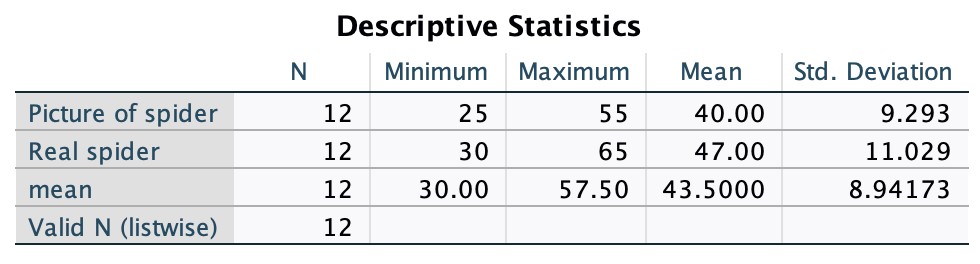
Step 3: Calculate the adjustment factor
Next, we equalize the means between participants (i.e., adjust the scores in each condition such that when we take the mean score across conditions, it is the same for all participants). To do this, we calculate an adjustment factor by subtracting each participant’s mean score from the grand mean. We can use the compute function to do this calculation for us. Activate the compute dialog box, give the target variable a name (I suggest adjustment) and then use the command ‘43.5-mean’. This command will take the grand mean (43.5) and subtract from it each participant’s average anxiety level (Figure 179).
This process creates a new variable in the data editor called adjustment. The scores in the adjustment column represent the difference between each participant’s mean anxiety and the mean anxiety level across all participants. You’ll notice that some of the values are positive, and these participants are one’s who were less anxious than average. Other participants were more anxious than average and they have negative adjustment scores. We can now use these adjustment values to eliminate the between-subject differences in anxiety.
Step 4: Create adjusted values for each variable
So far, we have calculated the difference between each participant’s mean score and the mean score of all participants (the grand mean). This difference can be used to adjust the existing scores for each participant. First we need to adjust the scores in the picture condition. Once again, we can use the compute command to make the adjustment. Activate the compute dialog box in the same way as before, and then title our new variable picture_adjusted. All we are going to do is to add each participant’s score in the picture condition to their adjustment value. Select the variable picture and drag it to the command area (or click  , then click on
, then click on  and drag the variable
and drag the variable adjustment to the command area (or click  ) - see Figure 180.
) - see Figure 180.
picture
Now do the same thing for the variable real: create a variable called real_adjusted that contains the values of real added to the value in the adjustment column (Figure 181)
real
Now, the variables real_adjusted and picture_adjusted represent the anxiety experienced in each condition, adjusted so as to eliminate any between-subject differences. You can plot an error bar graph using the chart builder. The finished dialog box will look like Figure 182:
The resulting error bar plot is in Figure 183. The error bars don’t overlap which suggests that the groups are significantly different (although we knew this already from the previous task).
Big Hairy Spider.sav
Task 10.3
‘Pop psychology’ books sometimes spout nonsense that is unsubstantiated by science. As part of my plan to rid the world of pop psychology I took 20 people in relationships and randomly assigned them to one of two groups. One group read the famous popular psychology book Women are from Bras and men are from Penis, and the other read Marie Claire. The outcome variable was their relationship happiness after their assigned reading. Were people happier with their relationship after reading the pop psychology book? (
penis.sav).
The main output for this example is in Figure 184, and we can obtain the effect size as \(\hat{d} = -0.91 [-1.79, -0.01]\) (Figure 185). This means that reading the self-help book reduced relationship happiness by about one standard deviation, which is a fairly massive effect.
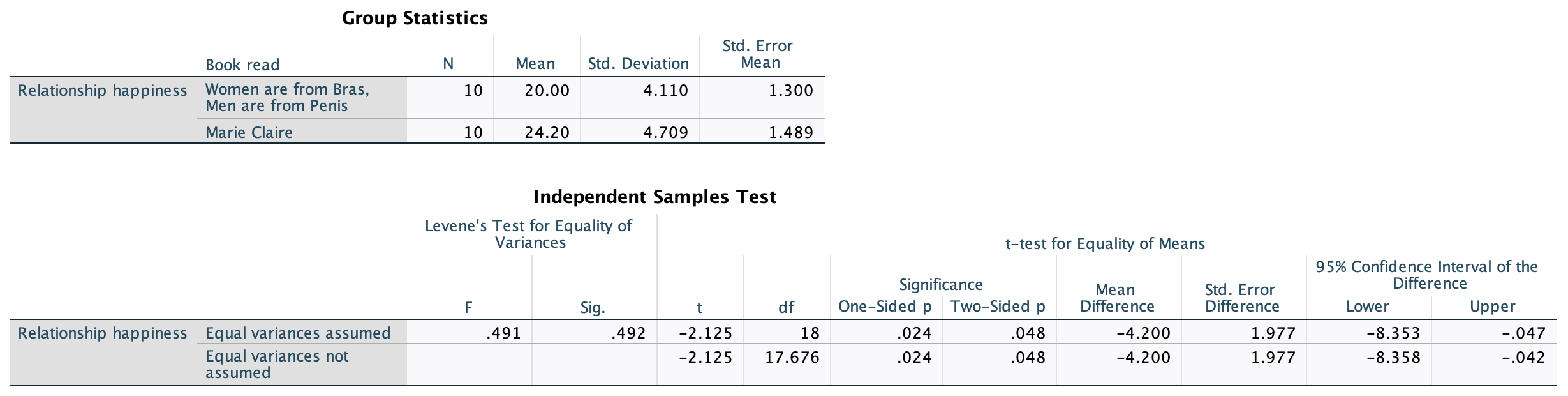
Task 10.4
Twaddle and Sons, the publishers of Women are from Bras and men are from Penis, were upset about my claims that their book was as useful as a paper umbrella. They ran their own experiment (N = 500) in which relationship happiness was measured after participants had read their book and after reading one of mine (Field & Hole, 2003). (Participants read the books in counterbalanced order with a six-month delay.) Was relationship happiness greater after reading their wonderful contribution to pop psychology than after reading my tedious tome about experiments? (
field_hole.sav).
The main output for this example is in Figure 186, and we can obtain the effect size as \(\hat{d} = 0.16 [0.04, 0.28]\) (Figure 187). Therefore, although this effect is highly statistically significant, the size of the effect is very small and represents a trivial finding. In this example, it would be tempting for Twaddle and Sons to conclude that their book produced significantly greater relationship happiness than our book. However, to reach such a conclusion is to confuse statistical significance with the importance of the effect. By calculating the effect size we’ve discovered that although the difference in happiness after reading the two books is statistically different, the size of effect that this represents is very small. Of course, this latter interpretation would be unpopular with Twaddle and Sons who would like to believe that their book had a huge effect on relationship happiness.
Task 10.5
In Chapter 4 (Task 6) we looked at data from people who had fish or cats as pets and measured their life satisfaction as well as how much they like animals (pets.sav). Conduct a t-test to see whether life satisfaction depends upon the type of pet a person has.
The main output for this example is in Figure 188, and we can obtain the effect size as \(\hat{d} = -1.51 [-2.48, -0.50]\) (Figure 189). As well as being statistically significant, this effect is very large and so represents a substantive finding.
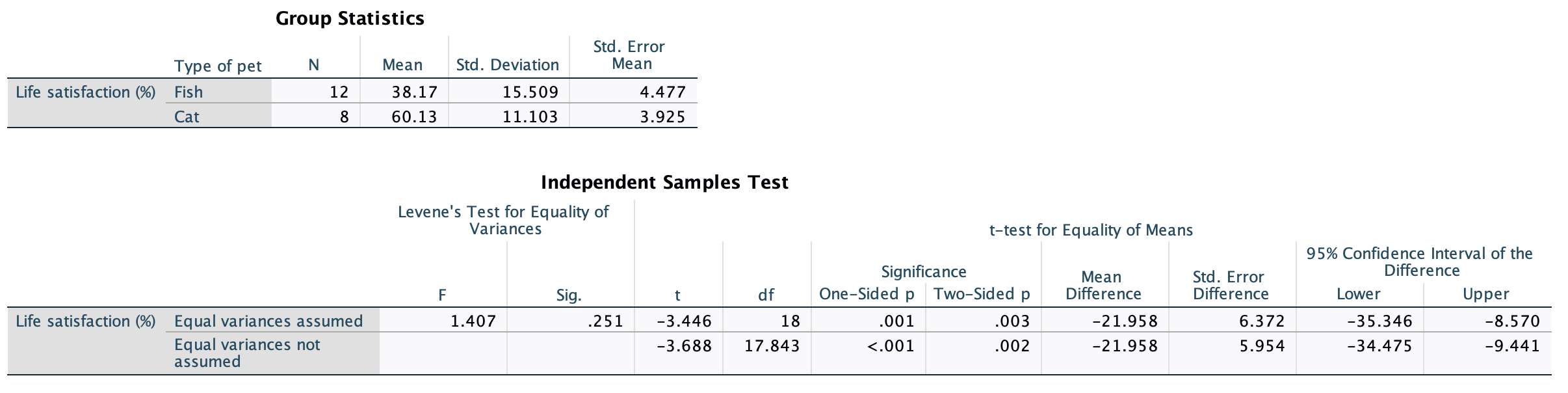
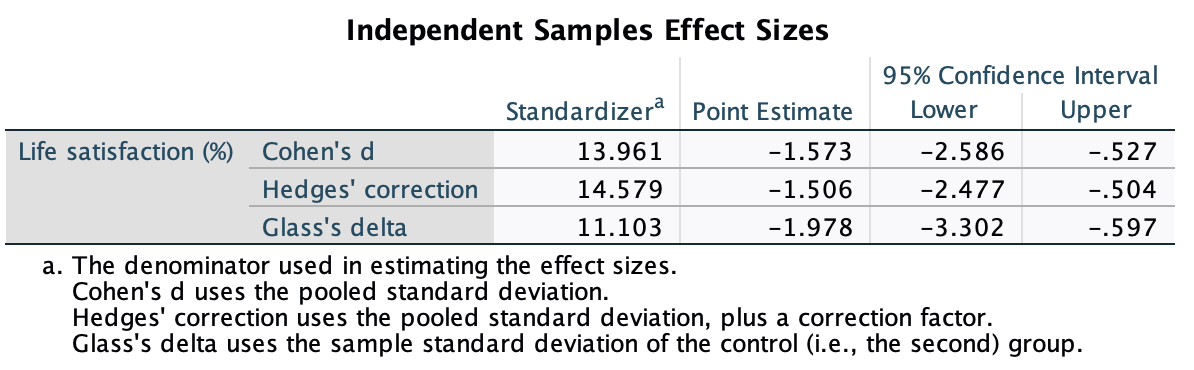
Task 10.6
Fit a linear model to the data in Task 5 to see whether life satisfaction is significantly predicted from the type of animal. What do you notice about the t-value and significance in this model compared to Task 5.
The output from the linear model is in Figure 190. Compare this output with the one from the previous task (Figure 188) the values of t and p are the same. (Technically, t is different because for the linear model it is a positive value and for the t-test it is negative However, the sign of t merely reflects which way around you coded the dog and goat groups. The linear model, by default, has coded the groups the opposite way around to the t-test.) The main point I wanted to make here is that whether you run these data through the regression or t-test menus, the results are identical.

Task 10.7
In Chapter 6 we looked at hygiene scores over three days of a rock music festival (
download.sav). Do a paired-samples t-test to see whether hygiene scores on day 1 differed from those on day 3.
The main output for this example is in Figure 191, and we can obtain the effect size as \(\hat{d} = 0.99 [0.76, 1.21]\) (Figure 192). This represents a very large effect. Therefore, as well as being statistically significant, this effect is large and represents a substantive finding.
Task 10.8
Analyse the data in Chapter 6, Task 1 (whether men and dogs differ in their dog-like behaviours) using an independent t-test with bootstrapping. Do you reach the same conclusions?
men_dogs.sav
The main output for this example is in Figure 193 and Figure 194. We would conclude that men and dogs do not significantly differ in the amount of dog-like behaviour they engage in. The output also shows the results of bootstrapping. The confidence interval ranged from -5.49 to 7.90, which implies (assuming that this confidence interval is one of the 95% containing the true effect) that the difference between means in the population could be negative, positive or even zero. In other words, it’s possible that the true difference between means is zero. Therefore, this bootstrap confidence interval confirms our conclusion that men and dogs do not differ in amount of dog-like behaviour. We can obtain the effect size as \(\hat{d} = 0.11 [-0.50, 0.72]\) (Figure 195) and this shows a small effect with a very wide confidence interval that crosses zero. Again, assuming that this confidence interval is one of the 95% containing the true effect., the effect in the population could be negative, positive or zero.
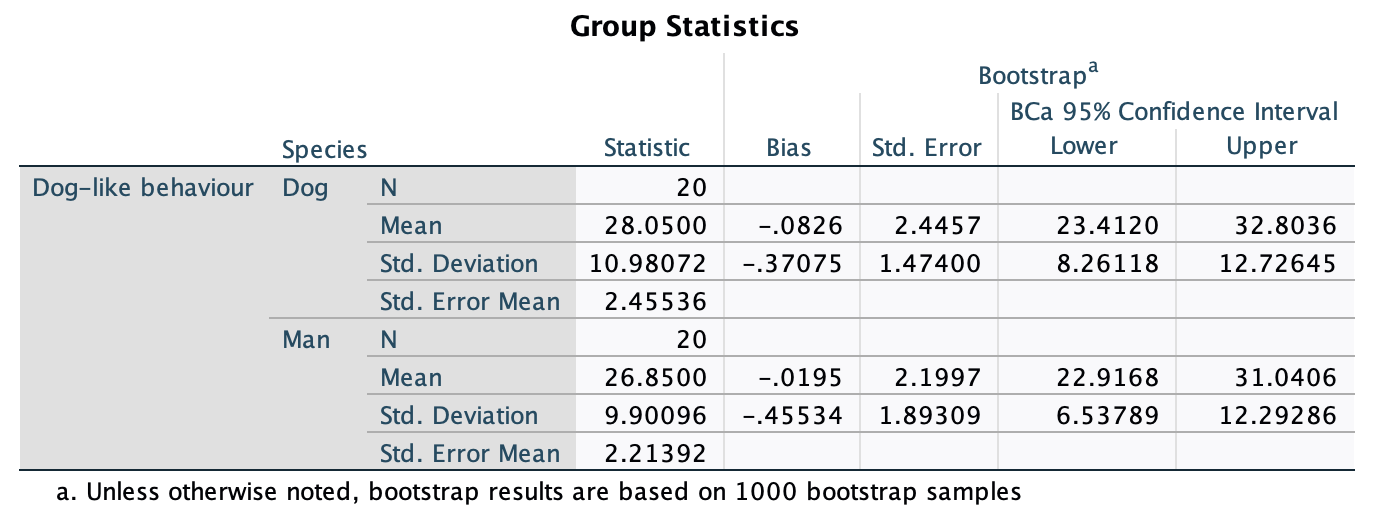
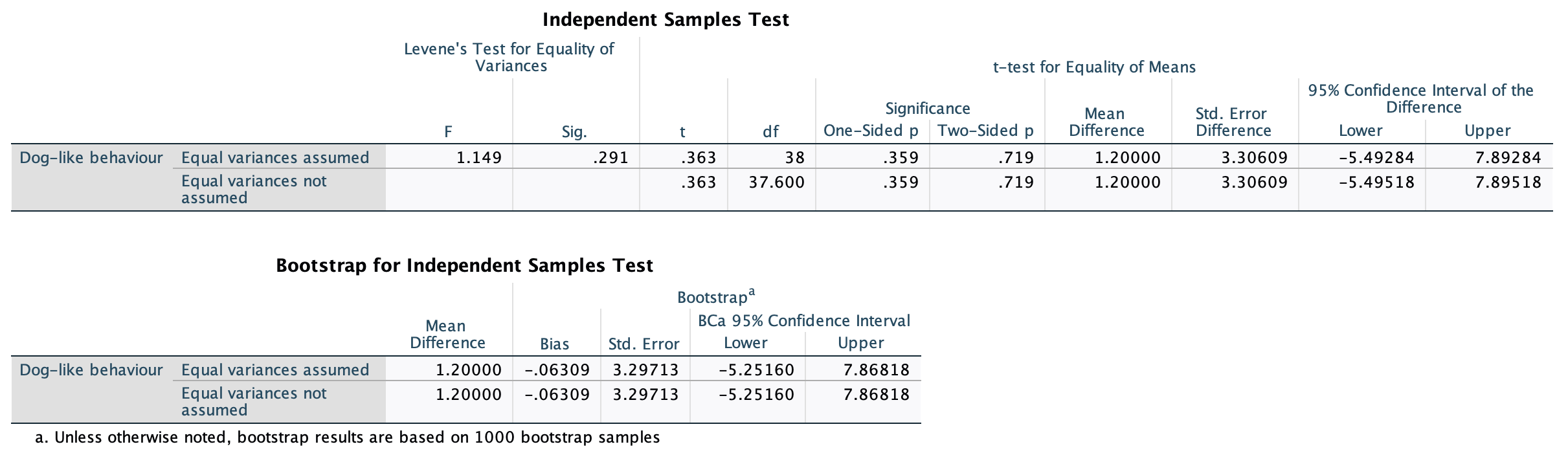
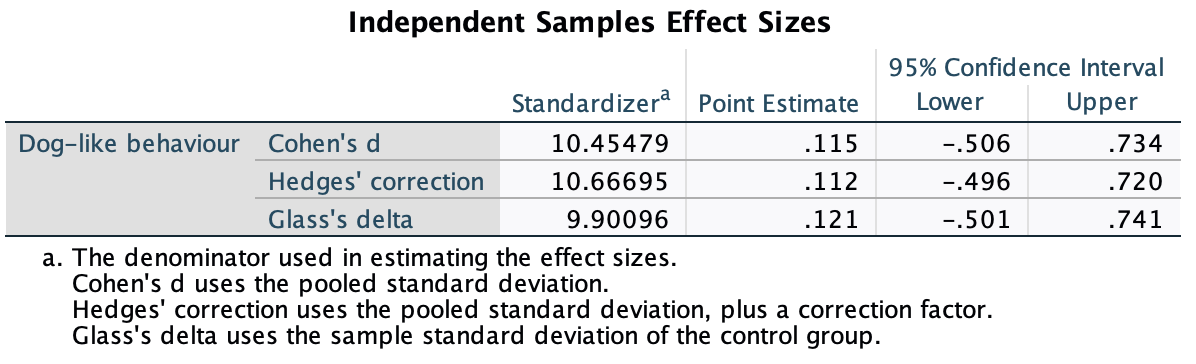
Task 10.9
Analyse the data in Chapter 6, Task 2 (whether the type of music you hear influences goat sacrificing –
dark_lord.sav), using a paired-samples t-test with bootstrapping. Do you reach the same conclusions?
The main output for this example is in Figure 196 and Figure 197. The bootstrap confidence interval ranges from -4.19 to -0.72. It does not cross zero suggesting (if we assume that it is one of the 95% of confidence intervals that contain the true value) that the effect in the population is unlikely to be zero. Therefore, this bootstrap confidence interval confirms our conclusion that there is a significant difference between the number of goats sacrificed when listening to the song containing the backward message compared to when listing to the song played normally. We can obtain the effect size as \(\hat{d} = -0.48 [-0.83, -0.12]\) (Figure 197). This represents a fairly large effect.
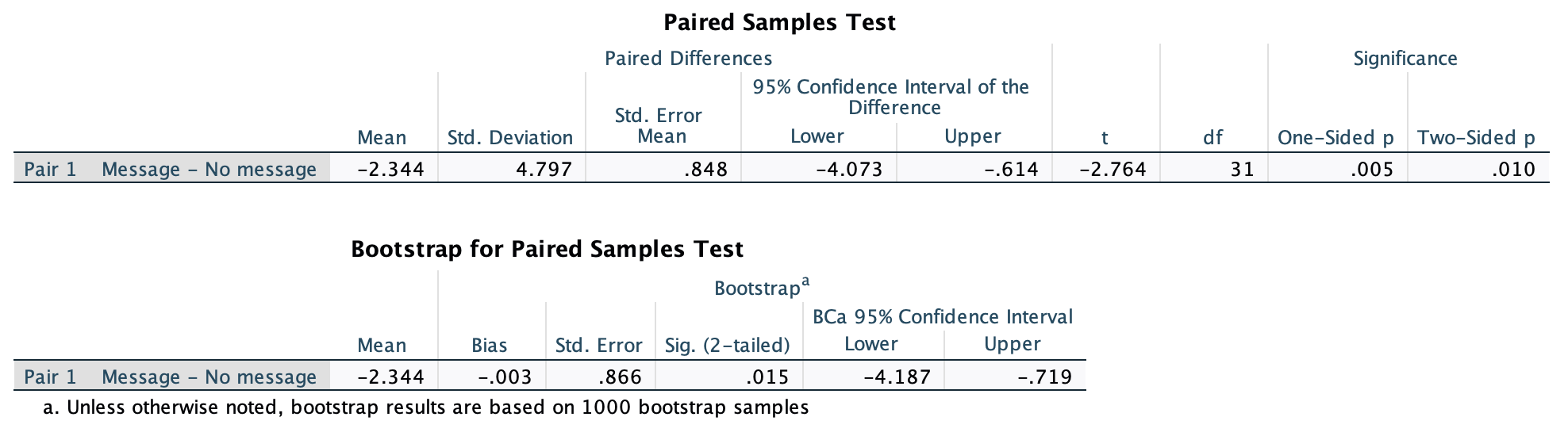 #fig-10_9b}
#fig-10_9b}
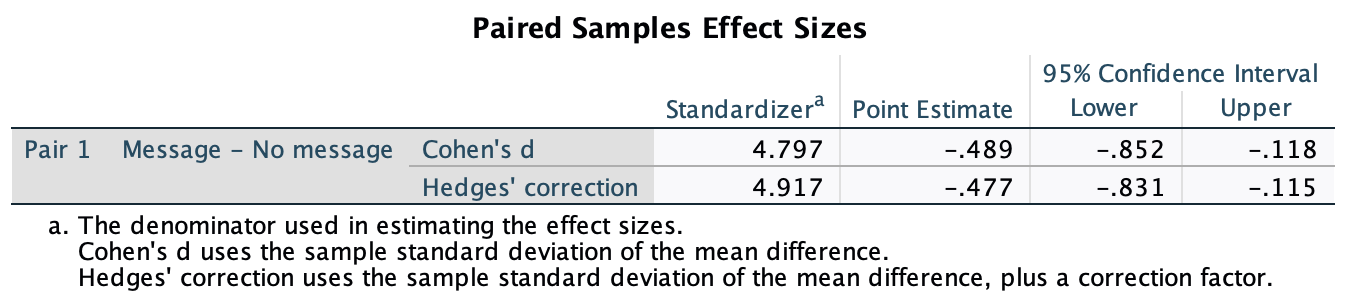
Task 10.10
Thinking back to Labcoat Leni’s Real Research 4.1 test whether the number of offers was significantly different in people listening to Bon Scott than in those listening to Brian Johnson (
acdc.sav), using an independent t-test and bootstrapping. Do your results differ from Oxoby (2008)?
The main output for this example is in Figure 198 and Figure 199. The bootstrap confidence interval ranged from -1.399 to -0.045, which does not cross zero suggesting that (if we assume that it is one of the 95% of confidence intervals that contain the true value) that the effect in the population is unlikely to be zero. We can obtain the effect size as \(\hat{d} = -0.65 [-1.31, 0.01]\) (Figure 200).
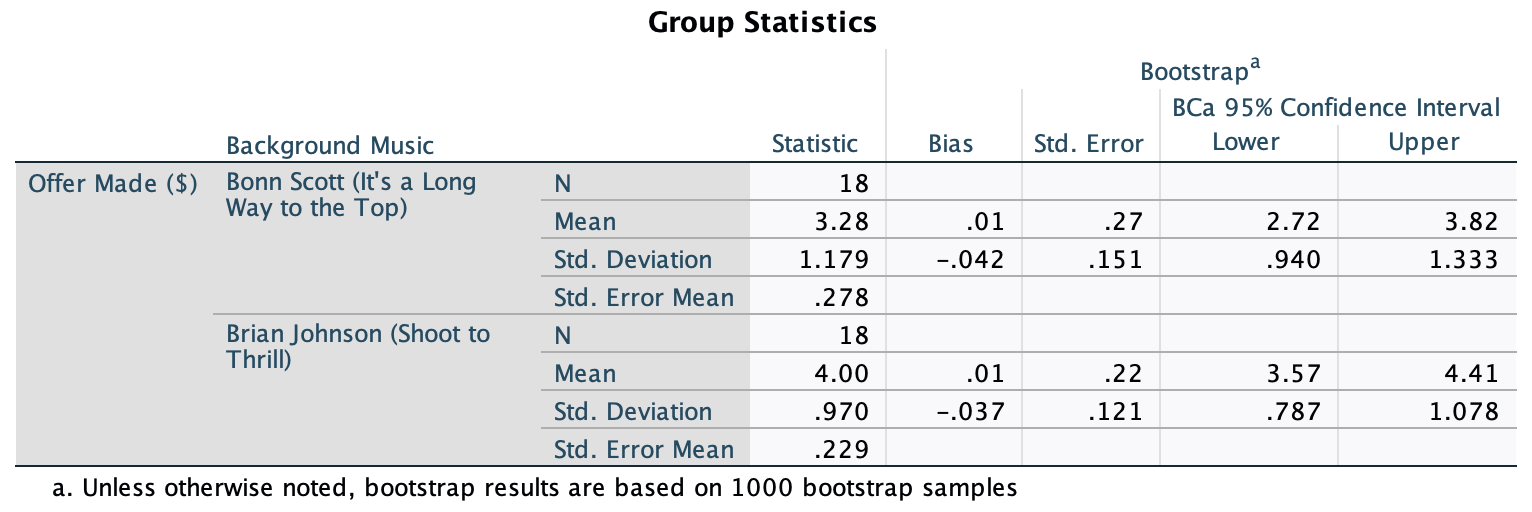
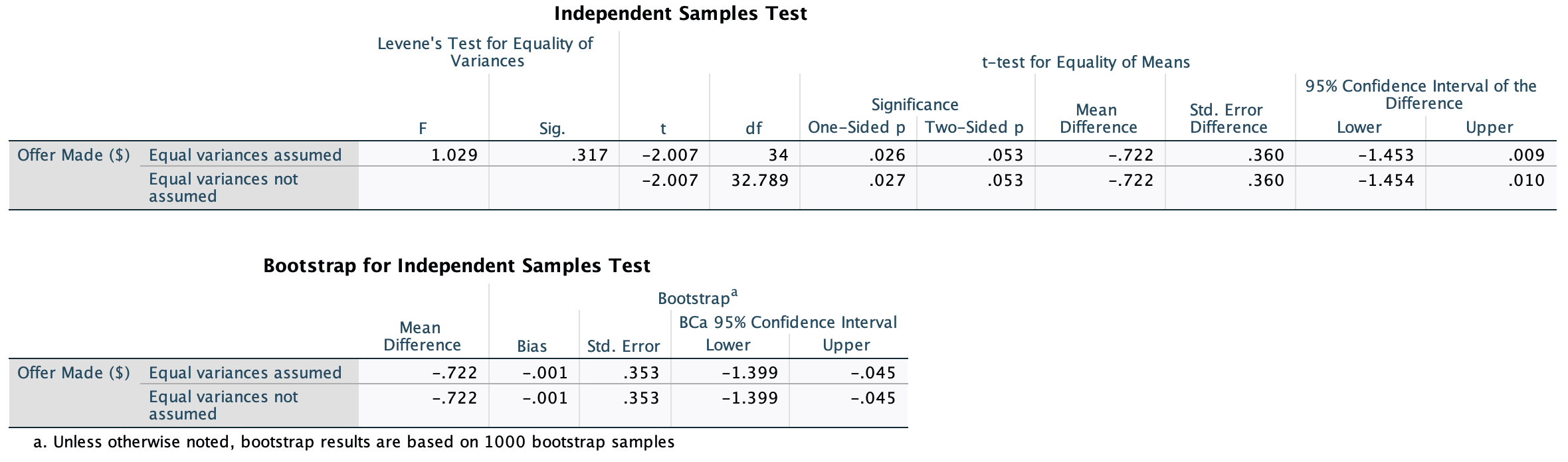
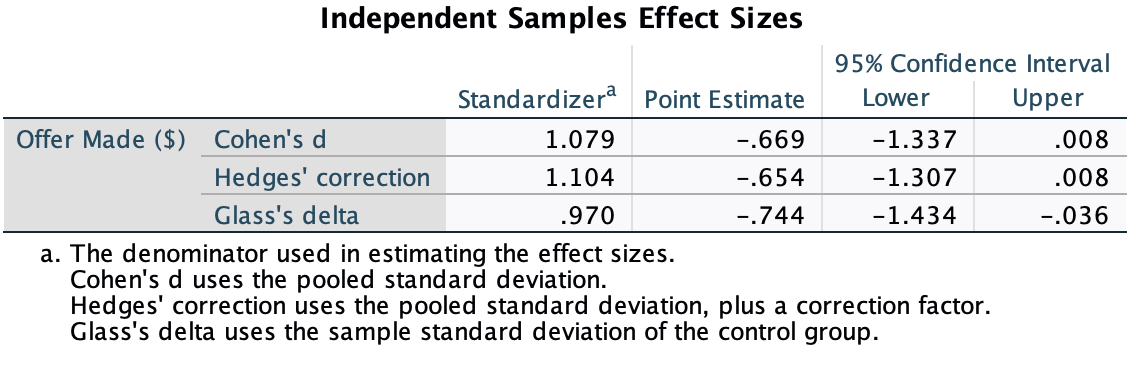
Chapter 11
Task 11.1
McNulty et al. (2008) found a relationship between a person’s attractiveness and how much
supportthey give their partner among newlywed heterosexual couples. The data are inmcnulty_2008.sav, Is this relationship moderated byspouse(i.e., whether the data were from the husband or wife)?
We need to specify three variables:
- Drag the outcome variable (
support) to the box labelled Y variable. - Drag the predictor variable (
attractiveness) to the box labelled X variable. - Drag the moderator variable (
spouse) to the box labelled Moderator variable W.
The models tested by PROCESS are listed in the drop-down box labelled Model number. Simple moderation analysis is represented by model 1, so activate this drop-down list and select  (Figure 201). Click on
(Figure 201). Click on  and set the options in Figure 202. Finally, because our data file has variables with names longer than 8 characters, click on
and set the options in Figure 202. Finally, because our data file has variables with names longer than 8 characters, click on  and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click
and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click  to run the analysis.
to run the analysis.
The first part of the output contains the main moderation analysis. Moderation is shown up by a significant interaction effect, and in this case the interaction is highly significant, b = 0.105, 95% CI [0.047, 0.164], t = 3.57, p < 0.001, indicating that the relationship between attractiveness and support is moderated by spouse:
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.2921 .0853 .0411 4.8245 3.0000 160.0000 .0030
Model
coeff se(HC4) t p LLCI ULCI
constant .1976 .0510 3.8721 .0002 .0968 .2984
attracti -.1652 .0462 -3.5751 .0005 -.2564 -.0739
spouse .0239 .0319 .7487 .4551 -.0391 .0869
Int_1 .1053 .0298 3.5395 .0005 .0466 .1641
Product terms key:
Int_1 : attracti x spouse
Test(s) of highest order unconditional interaction(s):
R2-chng F(HC4) df1 df2 p
X*W .0812 12.5280 1.0000 160.0000 .0005To interpret the moderation effect we can examine the simple slopes, which are shown in the next part of the output. Essentially, the output shows the results of two different regressions: the regression for attractiveness as a predictor of support (1) when the value for spouse is 1. Because husbands were coded as 1, this represents the value for husbands; and (2) when the value for gender is 2. Because wives were coded as 2, this represents wives. We can interpret these regressions as we would any other: we’re interested the value of b (called Effect in the output), and its significance. From what we have already learnt about regression we can interpret the two models as follows:
- For husbands (
spouse= 1), there is a significant negative relationship between attractiveness and support, b = 0.060, 95% CI [-0.100, -0.020], t = -2.95, p = 0.004. - for wives (
spouse= 2), there is a significant positive relationship between attractiveness and support, b = 0.046, 95% CI [0.003, 0.088], t = 2.12, p = 0.036.
These results tell us that the relationship between attractiveness of a person and amount of support given to their spouse is different for husbands and wives. Specifically, for wives, as attractiveness increases the level of support that they give to their husbands increases, whereas for husbands, as attractiveness increases the amount of support they give to their wives decreases.
Focal predict: attracti (X)
Mod var: spouse (W)
Conditional effects of the focal predictor at values of the moderator(s):
spouse Effect se(HC4) t p LLCI ULCI
1.0000 -.0598 .0204 -2.9326 .0039 -.1001 -.0195
2.0000 .0455 .0217 2.1002 .0373 .0027 .0883Task 11.2
Produce the simple slopes plots for Task 1.
If you set the options that I suggested in task 1, your output should contain the syntax that you need to plot the simple slopes
DATA LIST FREE/
attracti spouse support .
BEGIN DATA.
-1.1720 1.0000 .2916
.0460 1.0000 .2188
1.1460 1.0000 .1530
-1.1720 2.0000 .1921
.0460 2.0000 .2475
1.1460 2.0000 .2976
END DATA.
GRAPH/SCATTERPLOT=
attracti WITH support BY spouse .In your workbook click ![]() to create a new syntax paragraph, copy and paste the syntax from the PROCESS output (above), and then click
to create a new syntax paragraph, copy and paste the syntax from the PROCESS output (above), and then click  .
.
The resulting plot (I have edited to include the lines and make the dots clearer in Figure 204) confirms our results from the simple slops analysis in the previous task. The direction of the relationship between attractiveness and support is different for husbands and wives: the two regression lines slope in different directions. Specifically, for husbands (blue line) the relationship is negative (the regression line slopes downwards), whereas for wives (green line) the relationship is positive (the regression line slopes upwards). Additionally, the fact that the lines cross indicates a significant interaction effect (moderation). So basically, we can conclude that the relationship between attractiveness and support is positive for wives (more attractive wives give their husbands more support), but negative for husbands (more attractive husbands give their wives less support than unattractive ones). Although they didn’t test moderation, this mimics the findings of McNulty et al. (2008).
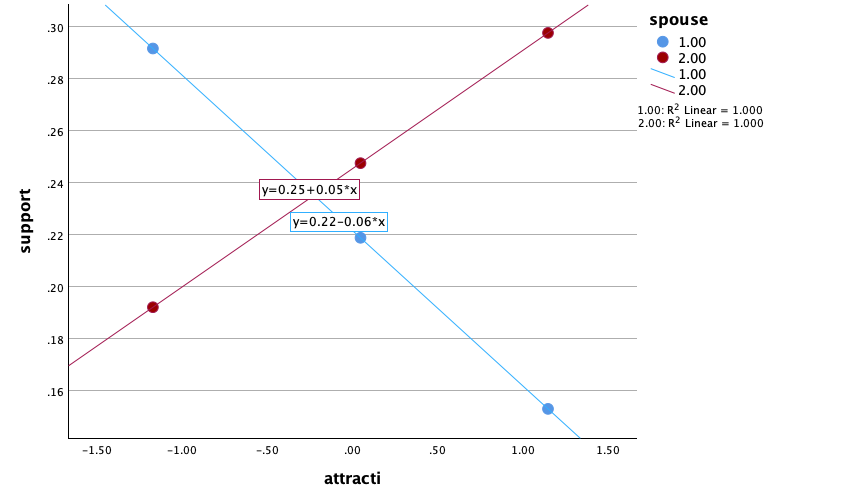
Task 11.3
McNulty et al. (2008) also found a relationship between a person’s
attractivenessand their relationshipsatisfactionamong newlyweds. Using the same data as in Tasks 1 and 2, find out if this relationship is moderated byspouse.
We need to specify three variables:
- Drag the outcome variable (
satisfaction) to the box labelled Y variable. - Drag the predictor variable (
attractiveness) to the box labelled X variable. - Drag the moderator variable (
spouse) to the box labelled Moderator variable W.
The models tested by PROCESS are listed in the drop-down box labelled Model number. Simple moderation analysis is represented by model 1, so activate this drop-down list and select  . The finished dialog box looks like Figure 205. Click on
. The finished dialog box looks like Figure 205. Click on  and set the options in Figure 202. Finally, because our data file has variables with names longer than 8 characters, click on
and set the options in Figure 202. Finally, because our data file has variables with names longer than 8 characters, click on  and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click
and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click  to run the analysis.
to run the analysis.
The first part of the output contains the main moderation analysis. Moderation is shown up by a significant interaction effect, and in this case the interaction is not significant, b = 0.547, 95% CI [-0.594, 1.687], t = 0.95, p = 0.345, indicating that the relationship between attractiveness and relationship satisfaction is not significantly moderated by spouse (i.e. the relationship between attractiveness and relationship satisfaction is not significantly different for husbands and wives)
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.1679 .0282 19.7492 2.0119 3.0000 160.0000 .1144
Model
coeff se(HC4) t p LLCI ULCI
constant 33.7513 .9889 34.1297 .0000 31.7983 35.7044
attracti -1.4305 .8748 -1.6352 .1040 -3.1581 .2972
spouse -.0236 .6959 -.0339 .9730 -1.3978 1.3507
Int_1 .5467 .5750 .9508 .3432 -.5889 1.6824
Product terms key:
Int_1 : attracti x spouse
Test(s) of highest order unconditional interaction(s):
R2-chng F(HC4) df1 df2 p
X*W .0048 .9039 1.0000 160.0000 .3432Task 11.4
In this chapter we tested a mediation model of infidelity for Lambert et al.’s data (Lambert et al., 2012). Repeat this analysis but using
hook_upsas the measure of infidelity.
We need to specify three variables:
- Drag the outcome variable (
hook_ups) to the box labelled Y variable. - Drag the predictor variable (
ln-porn) to the box labelled X variable. - Drag the mediator variable (
commit) to the box labelled Mediator(s) M.
The models tested by PROCESS are listed in the drop-down box labelled Model number. Simple mediation analysis is represented by model 4 (the default). If the drop-down list is not already set to  then select this option. The finished dialog box looks like Figure 206. Click on
then select this option. The finished dialog box looks like Figure 206. Click on  and set the options in Figure 207. Finally, because our data file has variables with names longer than 8 characters, click on
and set the options in Figure 207. Finally, because our data file has variables with names longer than 8 characters, click on  and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click
and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click  to run the analysis.
to run the analysis.

The first part of the output shows us the results of the linear model that predicts commitment from pornography consumption. Pornography consumption significantly predicts relationship commitment, b = -0.47, t = -1.99, p = 0.048. The \(R^2\) value tells us that pornography consumption explains 2% of the variance in relationship commitment, and the fact that the b is negative tells us that the relationship is negative also: as consumption increases, commitment declines (and vice versa).
OUTCOME VARIABLE:
commit
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.1418 .0201 .5354 3.9438 1.0000 237.0000 .0482
Model
coeff se(HC4) t p LLCI ULCI
constant 4.2027 .0530 79.2857 .0000 4.0983 4.3071
ln_porn -.4697 .2365 -1.9859 .0482 -.9356 -.0038
Standardized coefficients
coeff
ln_porn -.1418The next part of the output shows the results of the linear model that predicts the number of hook-ups from both pornography consumption and commitment. We can see that pornography consumption significantly predicts number of hook-ups even with relationship commitment in the model, b = 1.28, t = 2.41, p = 0.0169; relationship commitment also significantly predicts number of hook-ups, b = −0.62, t = −4.61, p < .001. The \(R^2\) value tells us that the model explains 14.0% of the variance in number of hook-ups. The negative b for commitment tells us that as commitment increases, number of hook-ups declines (and vice versa), but the positive b for consumptions indicates that as pornography consumption increases, the number of hook-ups increases also. These relationships are in the predicted direction.
OUTCOME VARIABLE:
hook_ups
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.3739 .1398 2.0411 12.2970 2.0000 236.0000 .0000
Model
coeff se(HC4) t p LLCI ULCI
constant 3.2427 .6124 5.2954 .0000 2.0363 4.4491
ln_porn 1.2811 .5325 2.4060 .0169 .2321 2.3301
commit -.6218 .1350 -4.6057 .0000 -.8877 -.3558
Standardized coefficients
coeff
ln_porn .1860
commit -.2990The next part of the output shows the total effect of pornography consumption on number of hook-ups (outcome). When relationship commitment is not in the model, pornography consumption significantly predicts the number of hook-ups, b = 1.57, t = 2.79, p = .006. The \(R^2\) value tells us that the model explains 5.22% of the variance in number of hook-ups. As is the case when we include relationship commitment in the model, pornography consumption has a positive relationship with number of hook-ups (as shown by the positive b-value).
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
hook_ups
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.2284 .0522 2.2395 7.8037 1.0000 237.0000 .0056
Model
coeff se(HC4) t p LLCI ULCI
constant .6296 .0967 6.5130 .0000 .4391 .8200
ln_porn 1.5731 .5631 2.7935 .0056 .4637 2.6825
Standardized coefficients
coeff
ln_porn .2284The next part of the output is the most important because it displays the results for the indirect effect of pornography consumption on number of hook-ups (i.e. the effect via relationship commitment). We’re told the effect of pornography consumption on the number of hook-ups when relationship commitment is included as a predictor as well (the direct effect). The first bit of new information is the Indirect effect(s) of X on Y, which in this case is the indirect effect of pornography consumption on the number of hook-ups. We’re given an estimate of this effect (b = 0.292) as well as a bootstrapped standard error and confidence interval. As we have seen many times before, 95% confidence intervals contain the true value of a parameter in 95% of samples. Assuming our sample is one of the 95% that ‘hits’ the true value, we can infer that the true b-value for the indirect effect falls between 0.0135 and 0.6282. This range does not include zero, and remember that b = 0 would mean ‘no effect whatsoever’; therefore, the fact that the confidence interval does not contain zero means that there is likely to be a genuine indirect effect. Put another way, relationship commitment is a mediator of the relationship between pornography consumption and the number of hook-ups. The standardized effect is \(ab_{\text{CS}}\) = 0.042, 95% BCa CI [0.002, 0.086]. Again the confidence interval doesn’t include zero so under the usual assumptions, we can infer that the indirect effect is greater than ‘no effect’.
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se(HC4) t p LLCI ULCI c_cs
1.5731 .5631 2.7935 .0056 .4637 2.6825 .2284
Direct effect of X on Y
Effect se(HC4) t p LLCI ULCI c'_cs
1.2811 .5325 2.4060 .0169 .2321 2.3301 .1860
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
commit .2920 .1561 .0135 .6282
Completely standardized indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
commit .0424 .0214 .0020 .0863
*********** BOOTSTRAP RESULTS FOR REGRESSION MODEL PARAMETERS ************
OUTCOME VARIABLE:
commit
Coeff BootMean BootSE BootLLCI BootULCI
constant 4.2027 4.2014 .0529 4.0943 4.3027
ln_porn -.4697 -.4688 .2300 -.9283 -.0219
----------
OUTCOME VARIABLE:
hook_ups
Coeff BootMean BootSE BootLLCI BootULCI
constant 3.2427 3.2480 .6191 2.0912 4.5211
ln_porn 1.2811 1.2769 .5338 .2748 2.3723
commit -.6218 -.6226 .1365 -.9038 -.3695You could report the results as:
Task 11.5
Tablets like the iPad are very popular. A company owner was interested in how to make his brand of tablets more desirable. He collected data on how cool people perceived a product’s advertising to be (
advert_cool), how cool they thought the product was (product_cool), and how desirable they found the product (desirability). Test his theory that the relationship between cool advertising and product desirability is mediated by how cool people think the product is (tablets.sav). Am I showing my age by using the word ‘cool’?
We need to specify three variables:
- Drag the outcome variable (
desirability) to the box labelled Outcome Variable (Y). - Drag the predictor variable (
advert_cool) to the box labelled Independent Variable (X). - Drag the mediator variable (
product_cool) to the box labelled M Variable(s).
The models tested by PROCESS are listed in the drop-down box labelled Model Number. Simple mediation analysis is represented by model 4 (the default). If the drop-down list is not already set to  then select this option. The finished dialog box looks like Figure 208. Click on
then select this option. The finished dialog box looks like Figure 208. Click on  and set the options in Figure 207. Finally, because our data file has variables with names longer than 8 characters, click on
and set the options in Figure 207. Finally, because our data file has variables with names longer than 8 characters, click on  and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click
and set the option to accept the risks of long names (Figure 203). Back in the main dialog box, click  to run the analysis.
to run the analysis.
The first part of the output shows us the results of the linear model that predicts the perceived ‘coolness’ of the product from the perceived ‘coolness’ of the advertising. We can see that how cool people perceive the advertising to be significantly predicts how cool they think the product is, b = 0.15, t = 2.37, p = .018. The \(R^2\) value tells us that cool advertising explains 2.54% of the variance in how cool they think the product is, and the fact that the b is positive tells us that the relationship is positive also: the more ‘cool’ people think the advertising is, the more ‘cool’ they think the product is (and vice versa).
OUTCOME VARIABLE:
product_
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.1593 .0254 .5397 5.6393 1.0000 238.0000 .0184
Model
coeff se(HC4) t p LLCI ULCI
constant .5985 .1500 3.9897 .0001 .3030 .8941
advert_c .1517 .0639 2.3747 .0184 .0259 .2776
Standardized coefficients
coeff
advert_c .1593The next part of the output shows the results of the linear model predicting desirability from how cool people perceived both the advertising and product to be. Cool advertising significantly predicts product desirability even with product_cool in the model, b = 0.20, t = 3.06, p = .003; product_cool also significantly predicts product desirability, b = 0.23, t = 3.90, p < .001. The \(R^2\) values tells us that the model explains 11.04% of the variance in product desirability. The positive bs for product_cool and advert_cool tells us that as adverts and products increase in how cool they are perceived to be, product desirability increases also (and vice versa). These relationships are in the predicted direction.
OUTCOME VARIABLE:
desirabi
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.3323 .1104 .5085 16.6978 2.0000 237.0000 .0000
Model
coeff se(HC4) t p LLCI ULCI
constant 3.1107 .1364 22.8137 .0000 2.8420 3.3793
advert_c .2003 .0655 3.0574 .0025 .0712 .3294
product_ .2318 .0594 3.9041 .0001 .1148 .3487
Standardized coefficients
coeff
advert_c .2074
product_ .2286The next part of the output shows the total effect of cool advertising on product desirability (outcome). You will get this bit of the output only if you selected Total effect model. The total effect is the effect of the predictor on the outcome when the mediator is not present in the model. When product_cool is not in the model, cool advertising significantly predicts product desirability, b = .24, t = 3.62, p < .001. The \(R^2\) values tells us that the model explains 5.95% of the variance in product desirability. As is the case when we include product_cool in the model, advert_cool has a positive relationship with product desirability (as shown by the positive b-value).
************************** TOTAL EFFECT MODEL ****************************
OUTCOME VARIABLE:
desirabi
Model Summary
R R-sq MSE F(HC4) df1 df2 p
.2439 .0595 .5353 13.0797 1.0000 238.0000 .0004
Model
coeff se(HC4) t p LLCI ULCI
constant 3.2494 .1399 23.2222 .0000 2.9737 3.5250
advert_c .2355 .0651 3.6166 .0004 .1072 .3637
Standardized coefficients
coeff
advert_c .2439The next part of the output is the most important because it displays the results for the indirect effect of cool advertising on product desirability (i.e. the effect via product_cool). First, we’re again told the effect of cool advertising on the product desirability in isolation (the total effect). Next, we’re told the effect of cool advertising on the product desirability when product_cool is included as a predictor as well (the direct effect). The first bit of new information is the Indirect effect(s) of X on Y, which in this case is the indirect effect of cool advertising on the product desirability. We’re given an estimate of this effect (b = 0.035) as well as a bootstrapped standard error and confidence interval. As we have seen many times before, 95% confidence intervals contain the true value of a parameter in 95% of samples. Assuming our sample is one of the 95% that ‘hits’ the true value, we can infer that the true b-value for the indirect effect falls between 0.0054 and 0.0767. This range does not include zero, and remember that b = 0 would mean ‘no effect whatsoever’; therefore, the fact that the confidence interval does not contain zero means that there is likely to be a genuine indirect effect. Put another way, product_cool is a mediator of the relationship between cool advertising and product desirability. The standardized effect is \(ab_{\text{CS}}\) = 0.04 95% BCa CI [.006, .079]. Again the confidence interval doesn’t include zero so unde rthe usual assumptions, we can infer that the indirect effect is greater than ‘no effect’.
************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y **************
Total effect of X on Y
Effect se(HC4) t p LLCI ULCI c_cs
.2355 .0651 3.6166 .0004 .1072 .3637 .2439
Direct effect of X on Y
Effect se(HC4) t p LLCI ULCI c'_cs
.2003 .0655 3.0574 .0025 .0712 .3294 .2074
Indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
product_ .0352 .0179 .0054 .0767
Completely standardized indirect effect(s) of X on Y:
Effect BootSE BootLLCI BootULCI
product_ .0364 .0185 .0056 .0790
*********** BOOTSTRAP RESULTS FOR REGRESSION MODEL PARAMETERS ************
OUTCOME VARIABLE:
product_
Coeff BootMean BootSE BootLLCI BootULCI
constant .5985 .5976 .1489 .3043 .8886
advert_c .1517 .1520 .0627 .0268 .2761
----------
OUTCOME VARIABLE:
desirabi
Coeff BootMean BootSE BootLLCI BootULCI
constant 3.1107 3.1083 .1341 2.8445 3.3691
advert_c .2003 .2006 .0644 .0693 .3223
product_ .2318 .2326 .0585 .1188 .3477
Chapter 12
Task 12.1
To test how different teaching methods affected students’ knowledge I took three statistics modules (
group) where I taught the same material. For one module I wandered around with a large cane and beat anyone who asked daft questions or got questions wrong (punish). In the second I encouraged students to discuss things that they found difficult and gave anyone working hard a nice sweet (reward). In the final course I neither punished nor rewarded students’ efforts (indifferent). I measured the students’ exam marks (exam). The data are in the fileteaching.sav. Fit a model with planned contrasts to test the hypotheses that: (1) reward results in better exam results than either punishment or indifference; and (2) indifference will lead to significantly better exam results than punishment.
The first part of the output (Figure 209) shows the table of descriptive statistics. These diagnostics are important for interpretation later on: it looks as though marks are highest after reward and lowest after punishment.
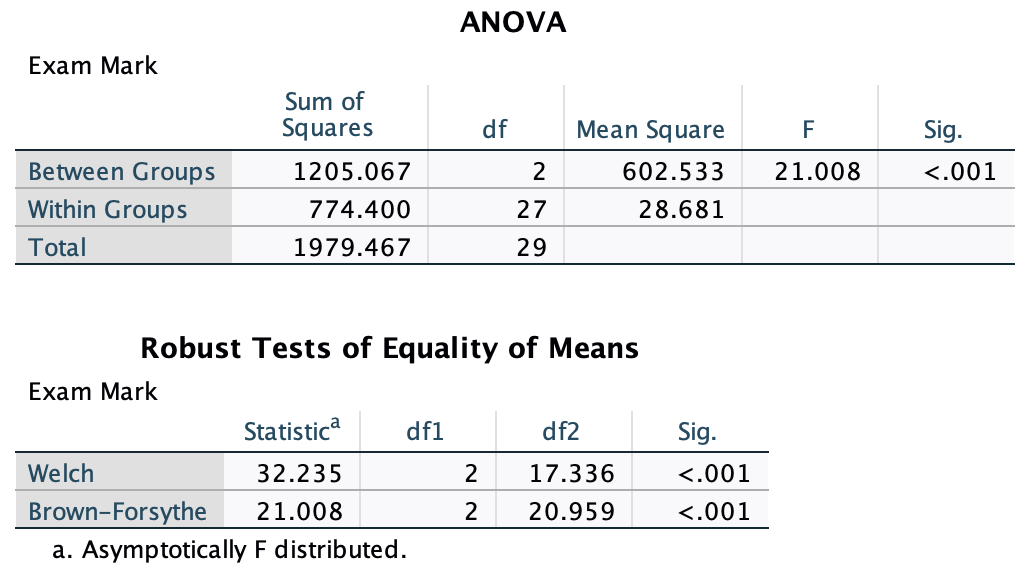
The next part of the output (Figure 210) is the main ANOVA summary table. We should routinely look at the robust Fs. Assuming we’re using a 0.05 criterion for significance, because the observed significance value is less than 0.05 we can say that there was a significant effect of teaching style on exam marks. This effect was fairly large, \(\omega^2\) = 0.57 [0.26, 0.70] (Figure 211).
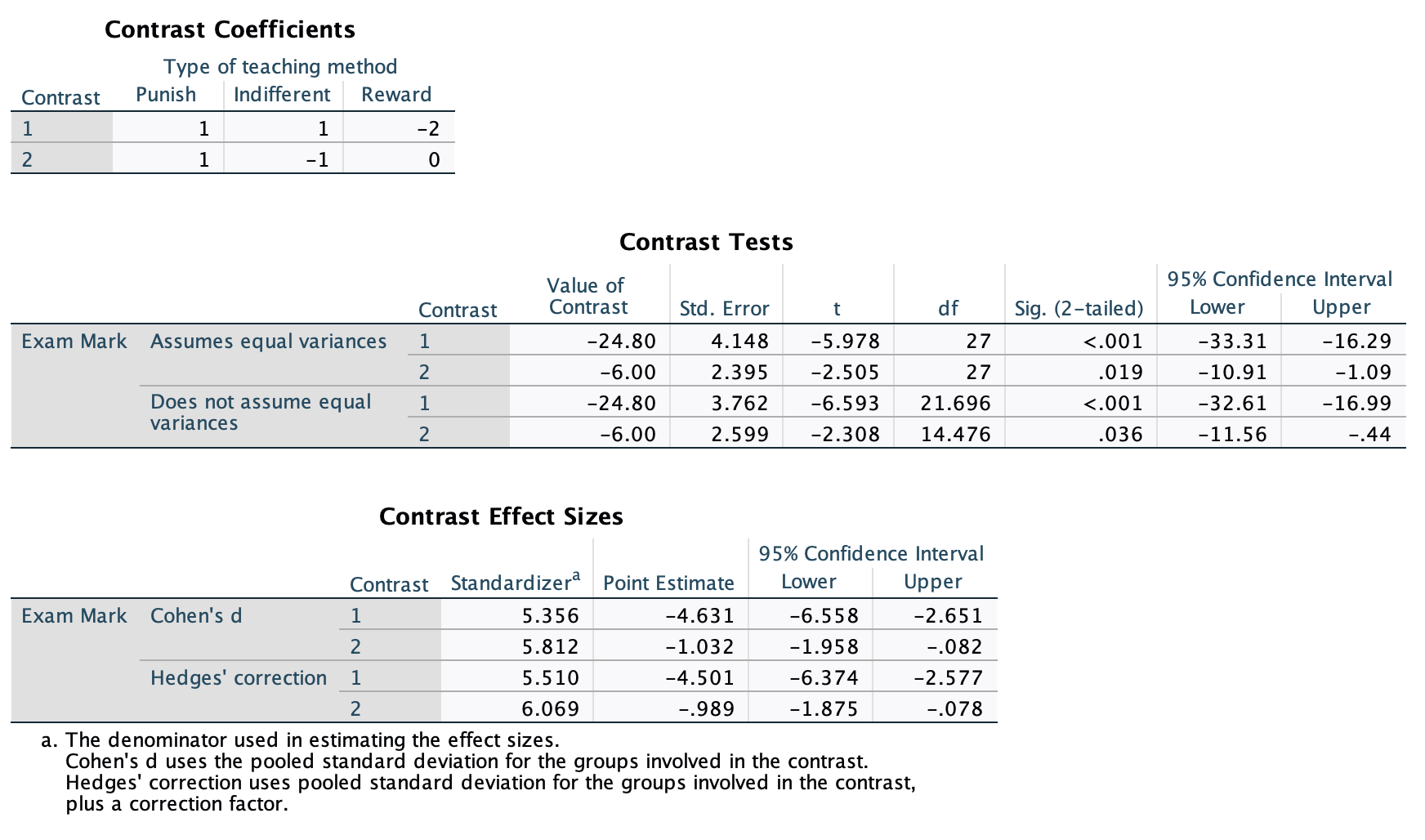
At this stage we do not know exactly what the effect of the teaching style was (we don’t know which groups differed). However, I specified contrasts to test the specific hypotheses in the question. The next part of the output shows the codes I used (Figure 212). The first contrast compares reward (coded with −2) against punishment and indifference (both coded with 1). The second contrast compares punishment (coded with 1) against indifference (coded with −1). Note that the codes for each contrast sum to zero, and that in contrast 2, reward has been coded with a 0 because it is excluded from that contrast.
It is safest to interpret the part of the table labelled Does not assume equal variances. The t-test for the first contrast tells us that reward was significantly different from punishment and indifference (it’s significantly different because the value in the column labelled Sig. is less than our criterion of 0.05). Looking at the direction of the means (Figure 209), this contrast suggests that the average mark after reward was significantly higher than the average mark for punishment and indifference combined. This is a massive1 effect \(\hat{d} = -4.50 \ [-6.37, -2.58]\). The second contrast (together with the descriptive statistics) tells us that the marks after punishment were significantly lower than after indifference (again, significantly different because the value in the column labelled Sig. is less than our criterion of 0.05). This effect is also very large, \(\hat{d} = -0.99 \ [-1.88, -0.08]\) As such we could conclude that reward produces significantly better exam grades than punishment and indifference, and that punishment produces significantly worse exam marks than indifference. In short, lecturers should reward their students, not punish them.
1 So big that if these were real data I’d be incredibly suspicious.

Task 12.2
Fit a robust model for Task 1.
We can fit this model using the following syntax
BEGIN PROGRAM R.
library(WRS2)
mySPSSdata = spssdata.GetDataFromSPSS(factorMode = "labels")
t1waybt(exam~group, data = mySPSSdata, tr = 0.2, nboot = 1000)
mcppb20(exam~group, data = mySPSSdata, tr = 0.2, nboot = 1000)
END PROGRAM.The output is below and confirms the finding of the non-robust analysis (see the Write it up! box for the interpretation).
Call:
t1waybt(formula = exam ~ group, data = mySPSSdata, tr = 0.2,
nboot = 1000)
Effective number of bootstrap samples was 996.
Test statistic: 21.4559
p-value: 0.00301
Variance explained: 0.62
Effect size: 0.787
Warning message:
In t1waybt(exam ~ group, data = mySPSSdata, tr = 0.2, nboot = 1000) :
Some bootstrap estimates of the test statistic could not be computed.
Call:
mcppb20(formula = exam ~ group, data = mySPSSdata, tr = 0.2,
nboot = 1000)
psihat ci.lower ci.upper p-value
Punish vs. Indifferent -5.83333 -14.16667 1.16667 0.051
Punish vs. Reward -16.00000 -20.66667 -11.16667 0.000
Indifferent vs. Reward -10.16667 -16.50000 -2.00000 0.005Task 12.3
Children wearing superhero costumes are more likely to injure themselves because of the unrealistic impression of invincibility that these costumes could create. For example, children have reported to hospital with severe injuries because of trying ‘to initiate flight without having planned for landing strategies’ (Davies et al., 2007). I can relate to the imagined power that a costume bestows upon you; indeed, I have been known to dress up as Fisher by donning a beard and glasses and trailing a goat around on a lead in the hope that it might make me more knowledgeable about statistics. Imagine we had data (
superhero.sav) about the severity ofinjury(on a scale from 0, no injury, to 100, death) for children reporting to the accident and emergency department at hospitals, and information on which superhero costume they were wearing (hero): Spiderman, Superman, the Hulk or a teenage mutant ninja turtle. Fit a model with planned contrasts to test the hypothesis that those wearing costumes of flying superheroes (Superman and Spiderman) have more severe injuries.
The means (Figure 213) suggest that children wearing a Ninja Turtle costume had the least severe injuries (M = 26.25), whereas children wearing a Superman costume had the most severe injuries (M = 60.33). Let’s assume we’re using \(\alpha = 0.05\). In the ANOVA output (we should routinely look at the robust Fs.), the observed significance value is much less than 0.05 and so we can say that there was a significant effect of superhero costume on injury severity (Figure 214). At this stage we still do not know exactly what the effect of superhero costume was (we don’t know which groups differed).
Because there were no specific hypotheses, only that the groups would differ, we can’t look at planned contrasts but we can conduct some post hoc tests. I am going to use Gabriel’s post hoc test because the group sizes are slightly different (Spiderman, N = 8; Superman, N = 6; Hulk, N = 8; Ninja Turtle, N = 8). The output (Figure 215) tells us that wearing a Superman costume was significantly different from wearing either a Hulk or Ninja Turtle costume in terms of injury severity, but that none of the other groups differed significantly.
The post hoc test has shown us which differences between means are significant; however, if we want to see the direction of the effects we can look back to the means in the table of descriptives (Figure 213). We can conclude that wearing a Superman costume resulted in significantly more severe injuries than wearing either a Hulk or a Ninja Turtle costume.
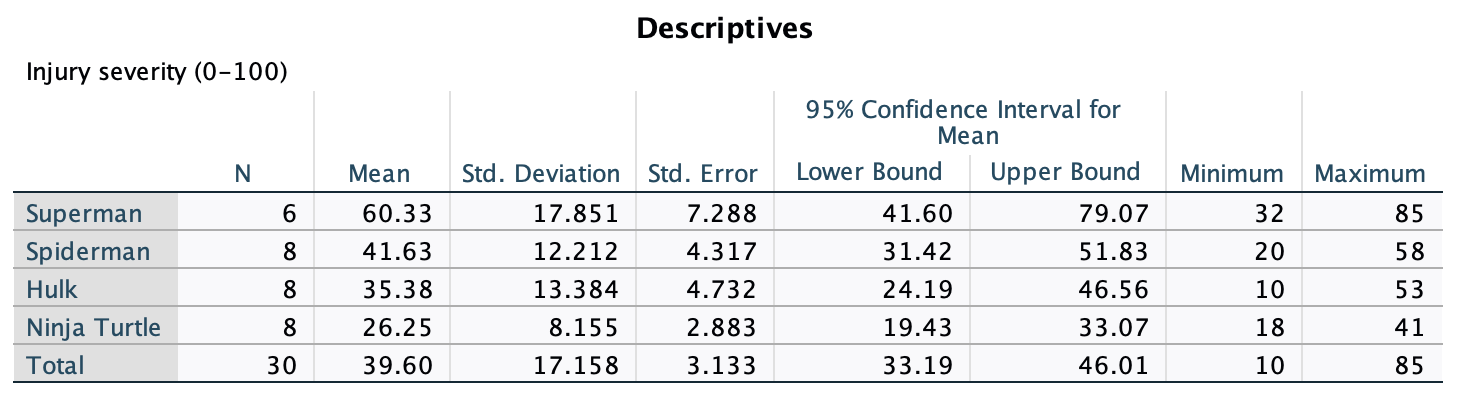
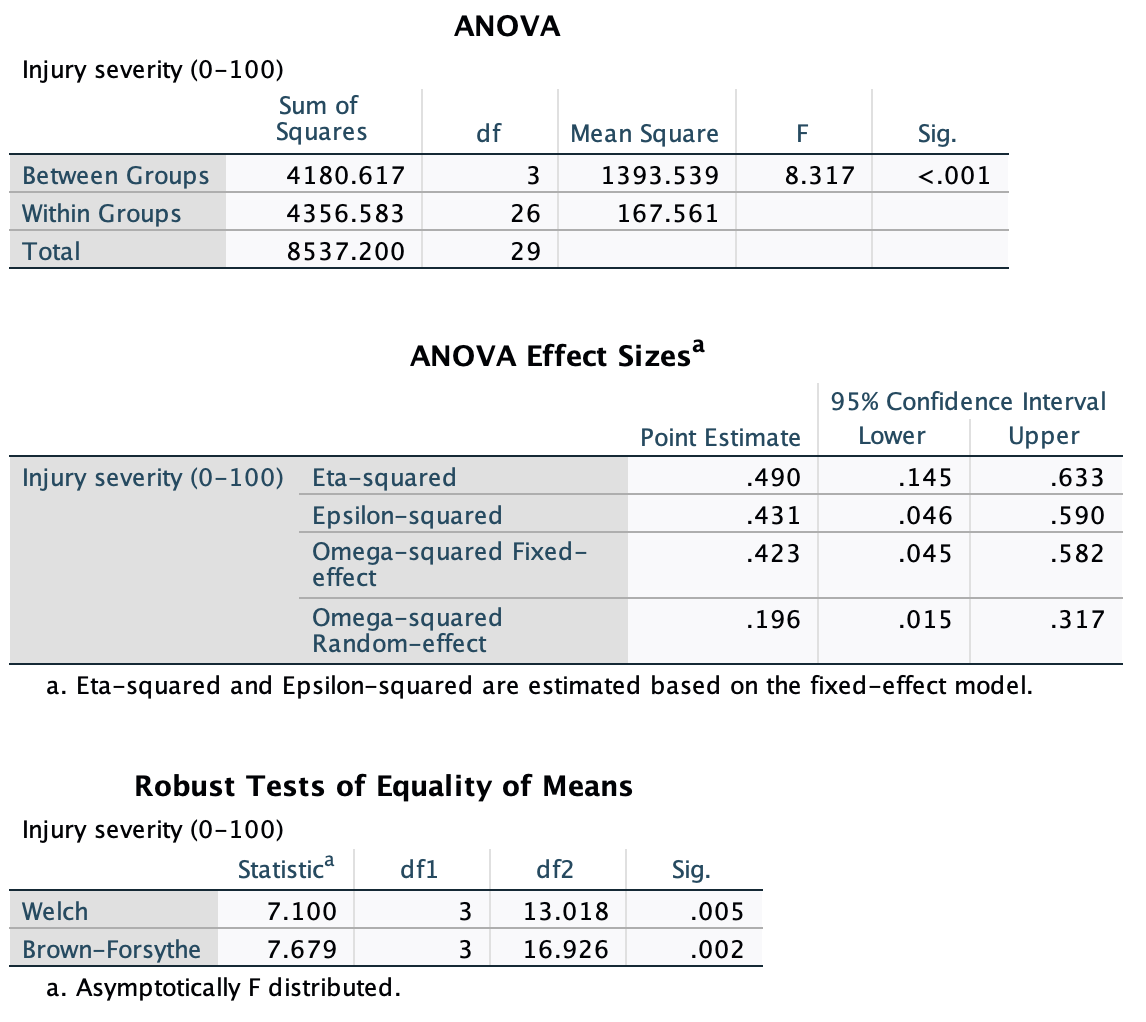
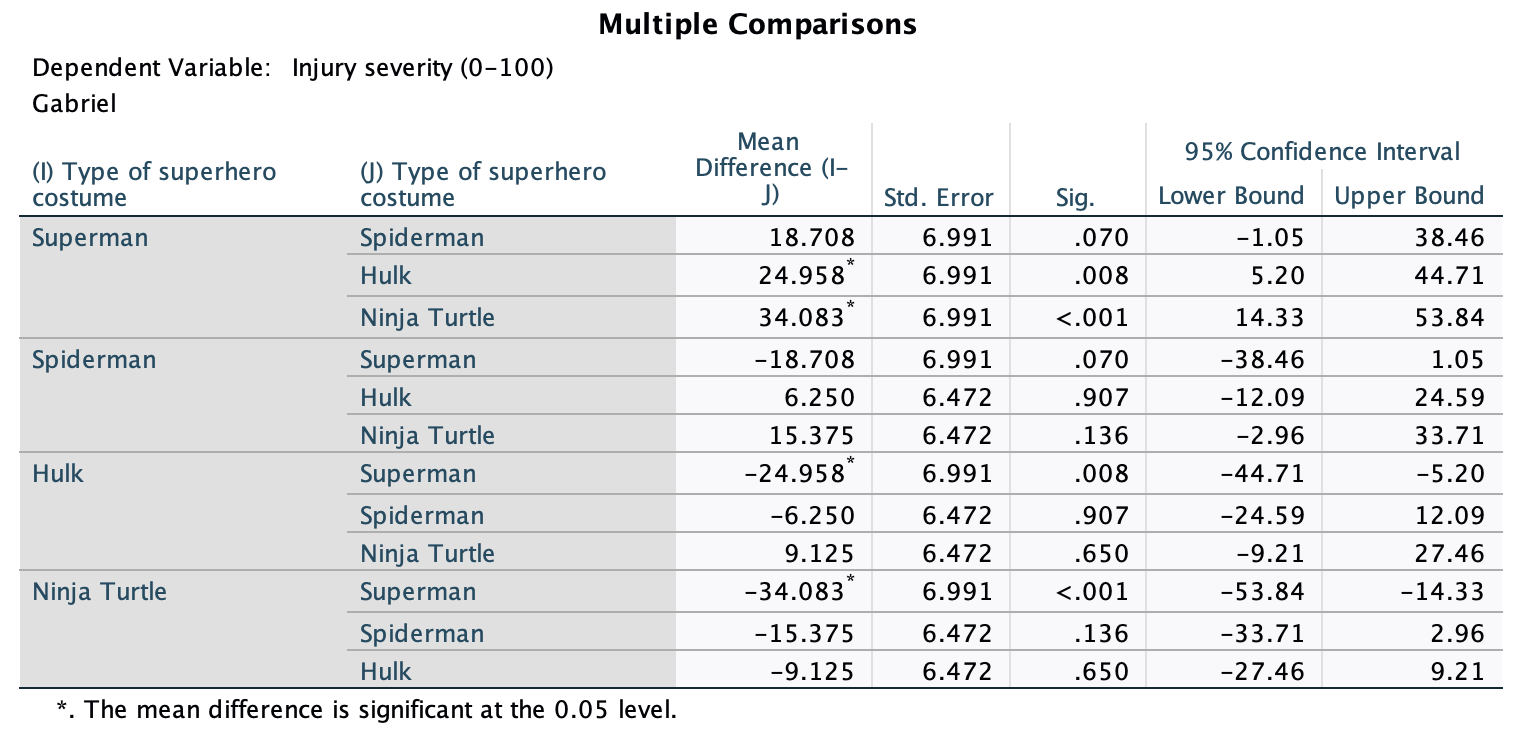
Task 12.4
In Chapter 6 (Section 7.6) there are some data looking at whether eating soya meals reduces your sperm count. Analyse these data with a linear model (ANOVA). What’s the difference between what you find and what was found in Section 7.6.5? Why do you think this difference has arisen? The data are in
soya.sav.
A boxplot of the data suggests that (1) scores within conditions are skewed; and (2) variability in scores is different across groups (Figure 216). The table of descriptive statistics suggests that as soya intake increases, sperm counts decrease as predicted (Figure 217). The next part of the output is the main ANOVA summary table (Figure 218). We should routinely look at the robust Fs. Note that the Welch test agrees with the non-parametric test in Chapter 7 in that the significance of F is below the 0.05 threshold. However, the Brown-Forsythe F is non-significant (it is just above the threshold). This illustrates the relative superiority (with respect to power) of the Welch procedure. The unadjusted F is also not significant. The effect size is very small, \(\omega^2\) = 0.06 [-0.04, 0.17], and if we assume that this sample is one of the 95% that produces a confidence interval capturing the true value then the effect could plausibly be zero.
If we were using the unadjusted F then we would conclude that, because the observed significance value is greater than 0.05, there was no significant effect of soya intake on men’s sperm count. This may seem strange because if you read Chapter 7, from where this example came, the Kruskal–Wallis test produced a significant result.The reason for this difference is that the data violate the assumptions of normality and homogeneity of variance. As I mention in Chapter 7, although parametric tests have more power to detect effects when their assumptions are met, when their assumptions are violated non-parametric tests have more power! This example was arranged to prove this point: because the parametric assumptions are violated, the non-parametric tests produced a significant result and the parametric test did not because, in these circumstances, the non-parametric test has the greater power. Also, the Welch F, which does adjust for these violations yields a significant result.
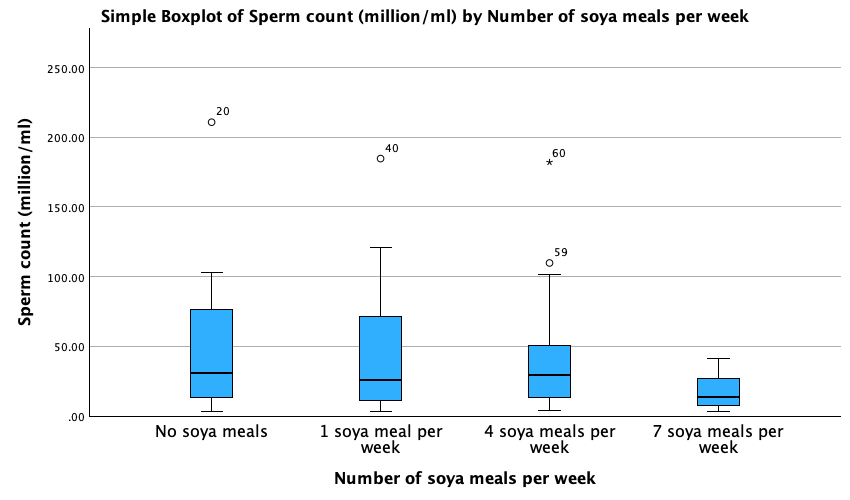
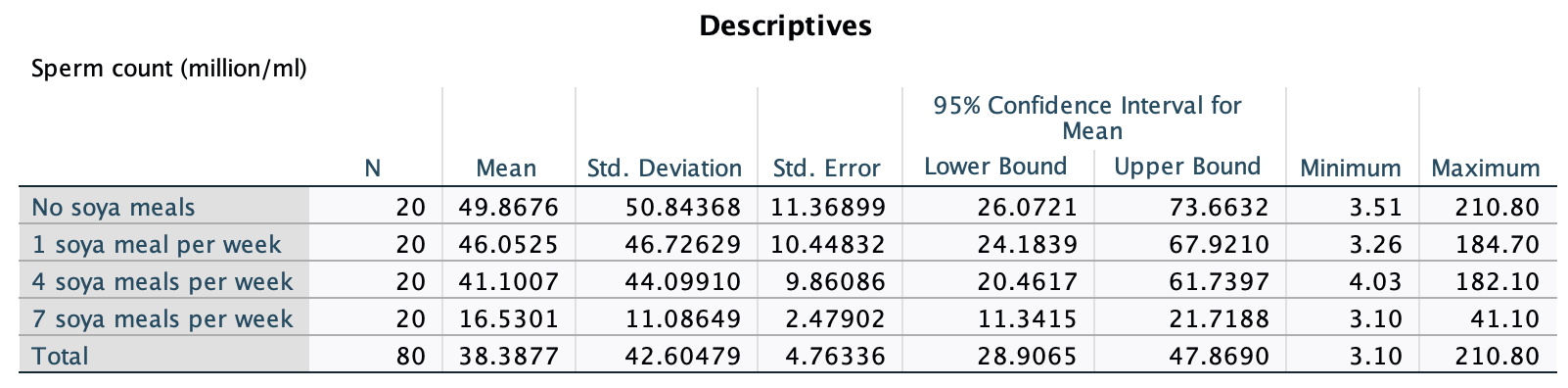
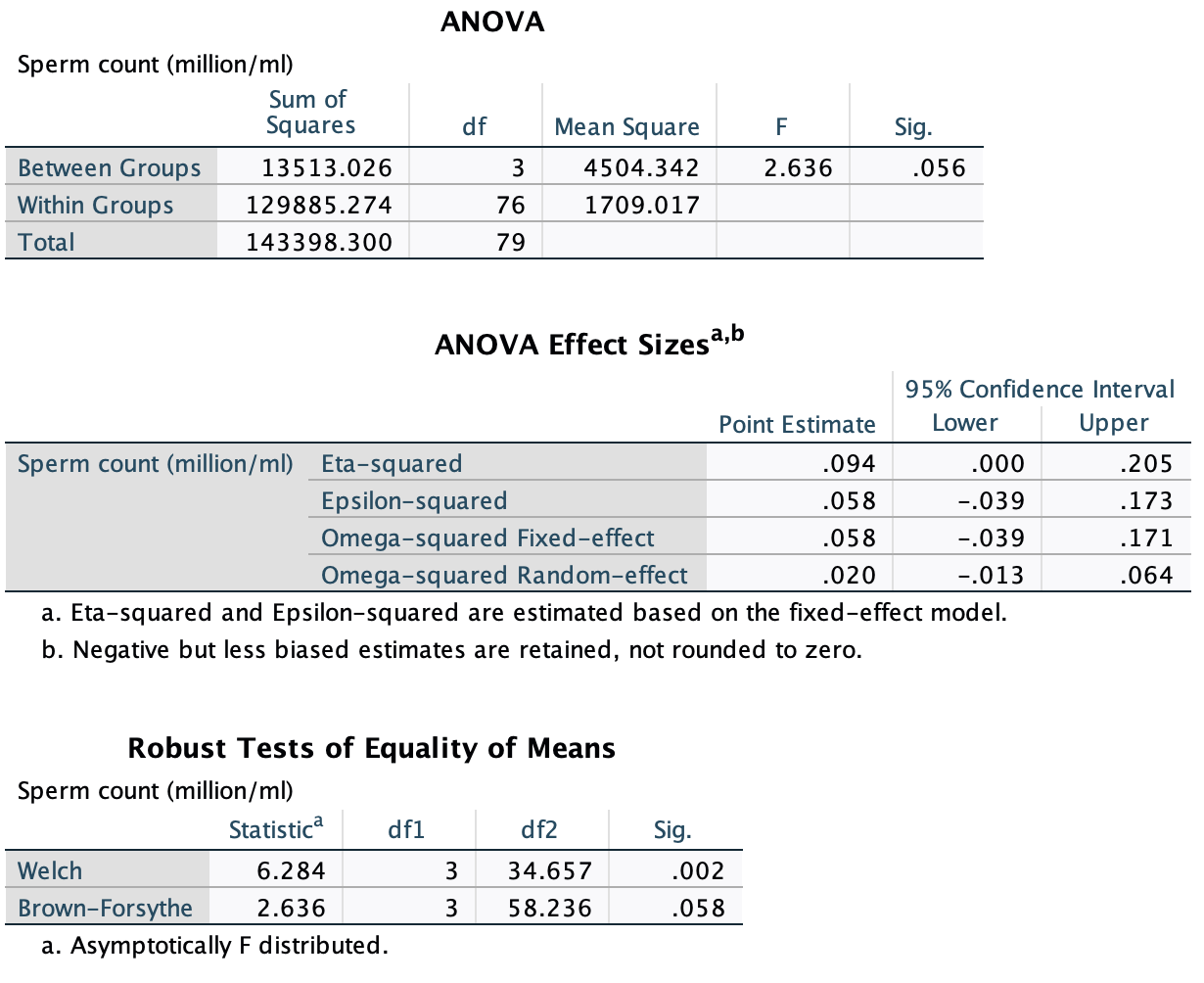
Task 12.5
Mobile phones emit microwaves, and so holding one next to your brain for large parts of the day is a bit like sticking your brain in a microwave oven and pushing the ‘cook until well done’ button. If we wanted to test this experimentally, we could get six groups of people and strap a mobile phone on their heads, then by remote control turn the phones on for a certain amount of time each day. After 6 months, we measure the size of any tumour (in mm3) close to the site of the phone antenna (just behind the ear). The six groups experienced 0, 1, 2, 3, 4 or 5 hours per day of phone microwaves for 6 months. Do tumours significantly increase with greater daily exposure? The data are in
tumour.sav.
Figure 219 displays the error bar chart of the mobile phone data. Note that in the control group (0 hours), the mean size of the tumour is virtually zero (we wouldn’t actually expect them to have a tumour) and the error bar shows that there was very little variance across samples - this almost certainly means we cannot assume equal variances. Figure 220 shows the table of descriptive statistics. The means should correspond to those plotted. These diagnostics are important for interpretation later on.
Figure 221 shows the main ANOVA summary table. We should routinely look at the robust Fs. Let’s assume we’re using \(\alpha\) = 0.05, because the observed significance of Welch’s F is less than 0.05 we can say that there was a significant effect of mobile phones on the size of tumour.
At this stage we still do not know exactly what the effect of the phones was (we don’t know which groups differed). Because there were no specific hypotheses I carried out post hoc tests and stuck to my favourite Games–Howell procedure (because variances were unequal). Each group of participants is compared to all of the remaining groups (Figure 222). First, the control group (0 hours) is compared to the 1, 2, 3, 4 and 5 hour groups and reveals a significant difference in all cases (all the values in the column labelled Sig. are less than 0.05). In the next part of the table, the 1 hour group is compared to all other groups. Again all comparisons are significant (all the values in the column labelled Sig. are less than 0.05). In fact, all of the comparisons appear to be highly significant except the comparison between the 4 and 5 hour groups, which is non-significant because the value in the column labelled Sig. is larger than 0.05.
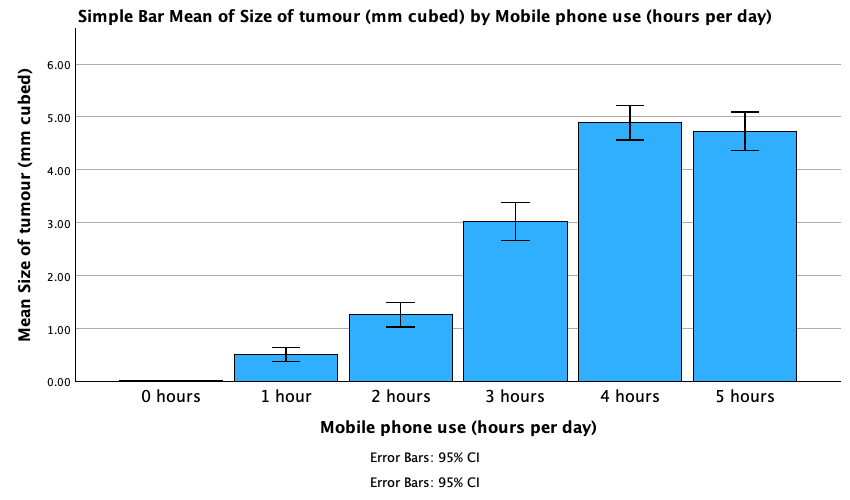
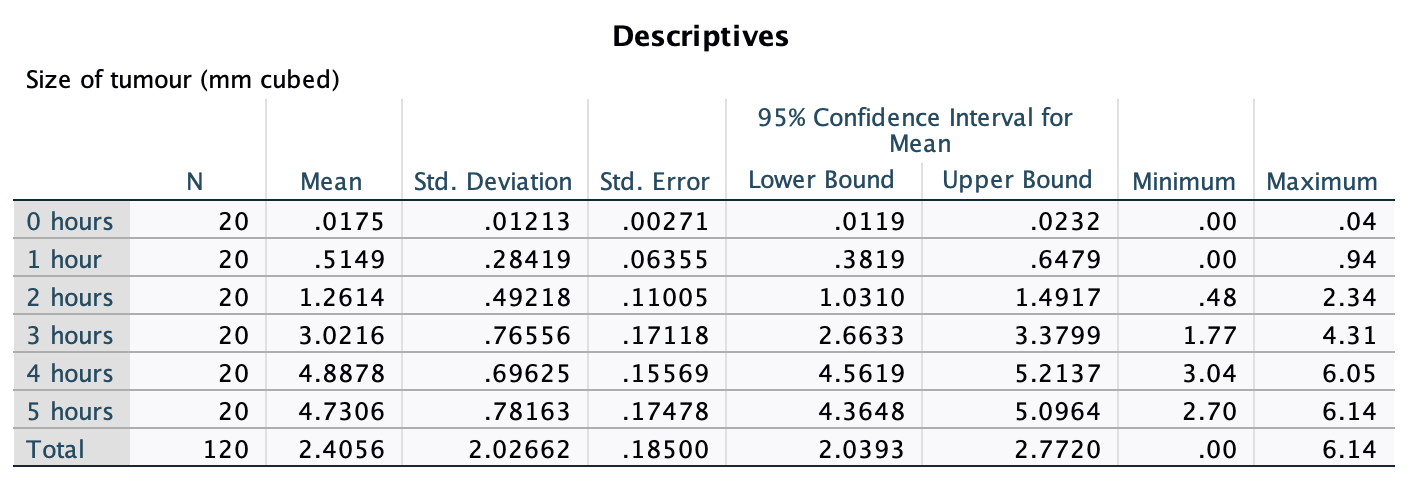
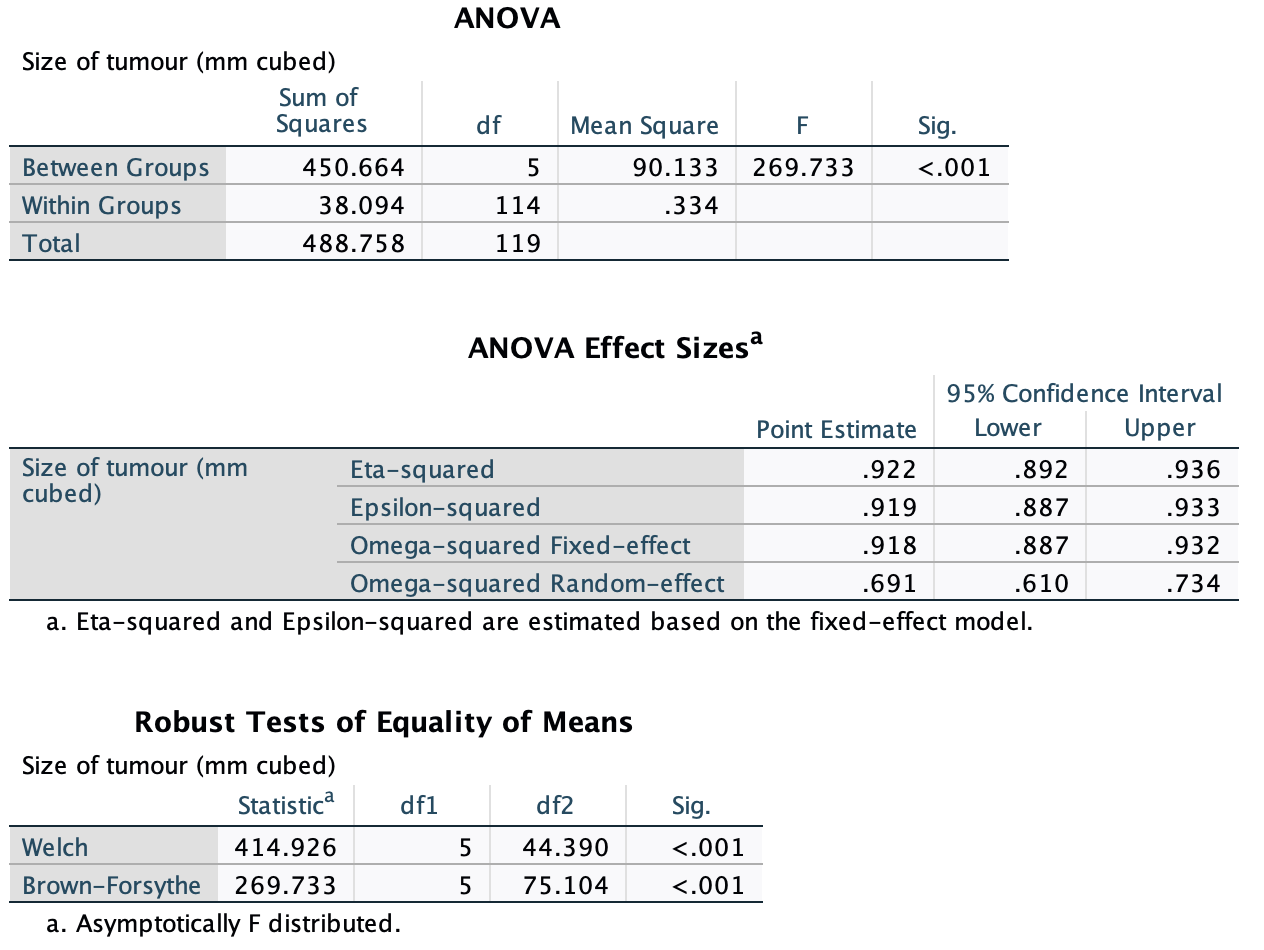
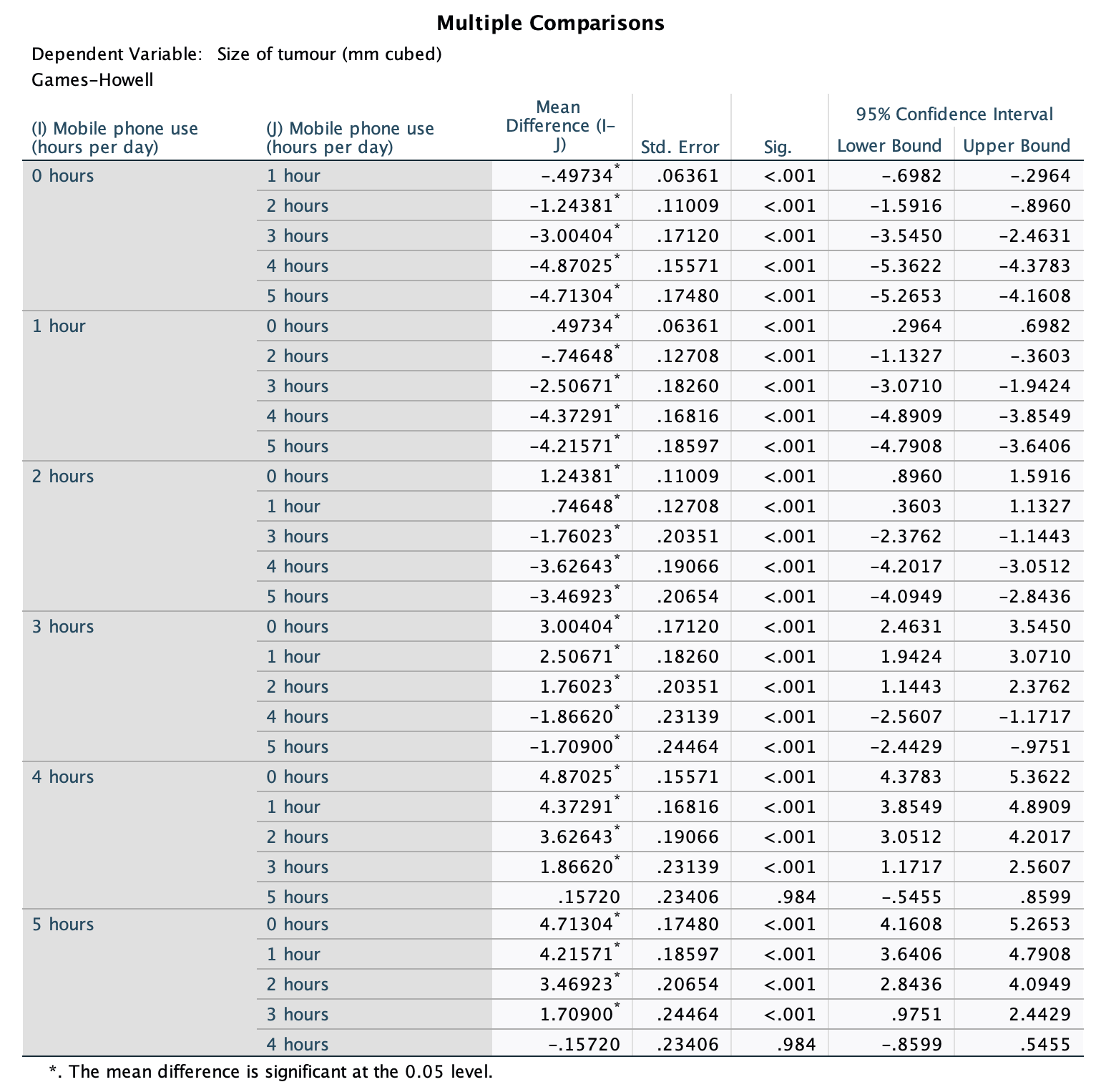
Task 12.6
Using the data in
glastonbury.sav, fit a model to see if the change in hygiene (change) is significant across people with different musical tastes (music). Use a simple contrast to compare each group against the no subculture group.
Figure 223 shows the main ANOVA table. Let’s assume we’re using \(\alpha\) = 0.05, because the observed significance of Welch’s F is less than 0.05 we can say that the change in hygiene scores was significantly different across the different musical subcultures, F(3, 43.19) = 3.08, p = 0.037.
Figure 224 shows the codes I used to get simple contrasts that compare each group to the no affiliation group, and the subsequent contrasts.
Task 12.7
Labcoat Leni’s Real Research 7.2 describes an experiment on quails with fetishes for terrycloth objects. There were two outcome variables (time spent near the terrycloth object and copulatory efficiency) that we didn’t analyse. Read Labcoat Leni’s Real Research 7.2 to get the full story then fit a model with Bonferroni post hoc tests on the time spent near the terrycloth object.
Figure 225 shows the descriptive statistics for each group. Figure 226 tells usb that the group (fetishistic, non-fetishistic or control group) had a significant effect on the time spent near the terrycloth object. The authors report the unadjusted F, although I would recommend using Welch’s F (not that it affects the conclusions from this model). To find out exactly what’s going on we can look at our post hoc tests (Figure 227). These results show that male quails do show fetishistic behaviour (the time spent with the terrycloth).
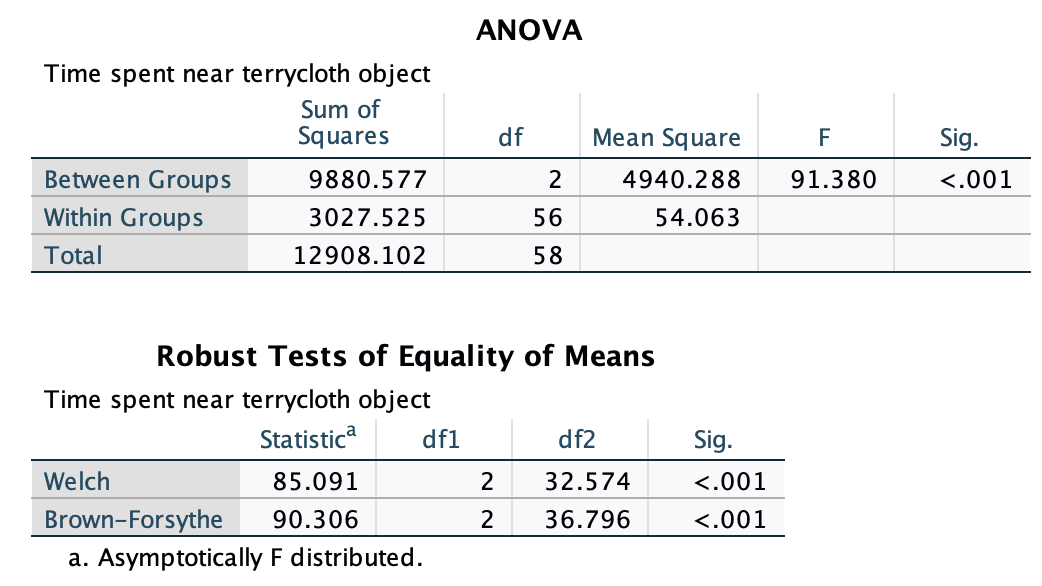
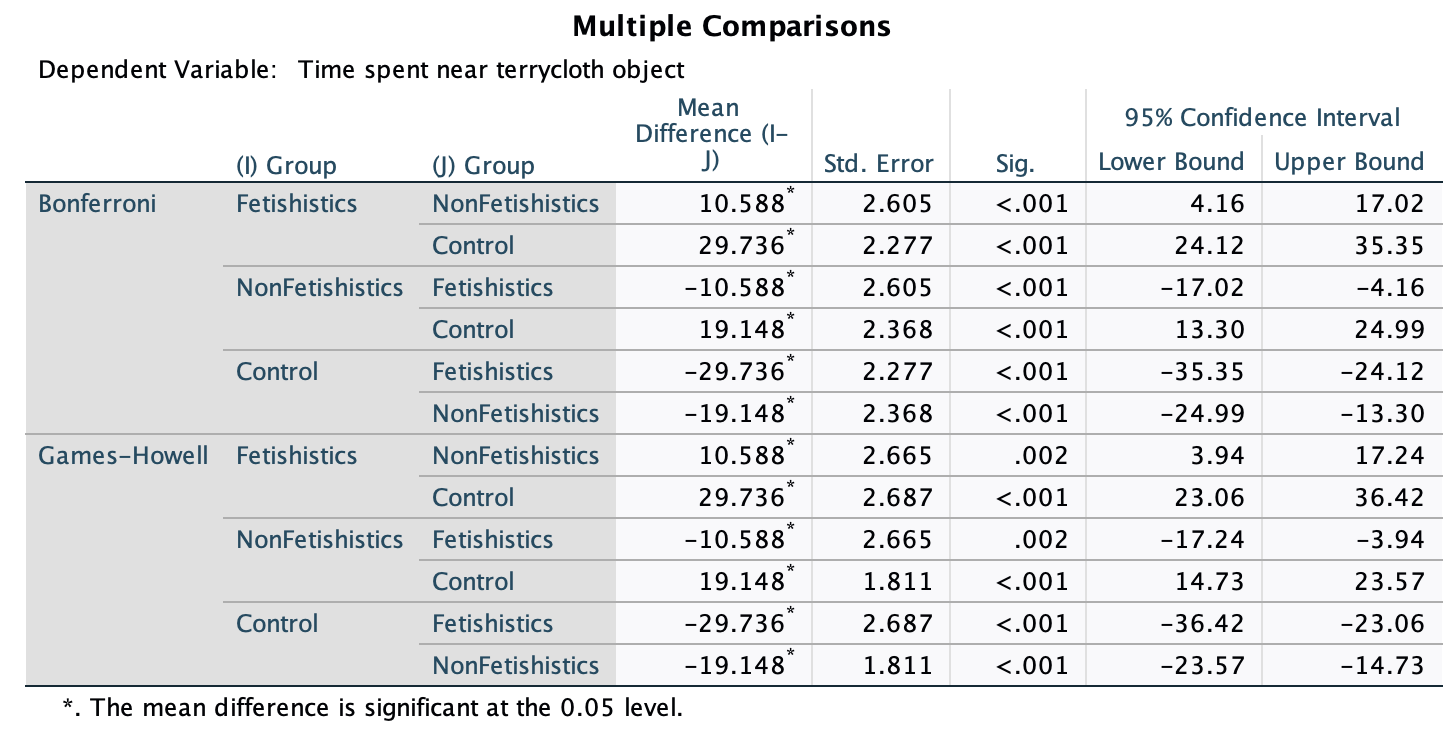
Task 12.8
Repeat the analysis in Task 7 but using copulatory efficiency as the outcome.
Figure 228 show the descriptive statistics. Figure 229 shows that the group (fetishistic, non-fetishistic or control group) had a significant effect on copulatory efficiency. The authors report the unadjusted F, although I would recommend using Welch’s F (not that it affects the conclusions from this model). To find out exactly what’s going on we can look at our post hoc tests (Figure 230).
These results show that male quails do show fetishistic behaviour (the time spent with the terrycloth – see Task 7 above) and that this affects their copulatory efficiency (they are less efficient than those that don’t develop a fetish, but it’s worth remembering that they are no worse than quails that had no sexual conditioning – the controls). If you look at Labcoat Leni’s box then you’ll also see that this fetishistic behaviour may have evolved because the quails with fetishistic behaviour manage to fertilize a greater percentage of eggs (so their genes are passed on).
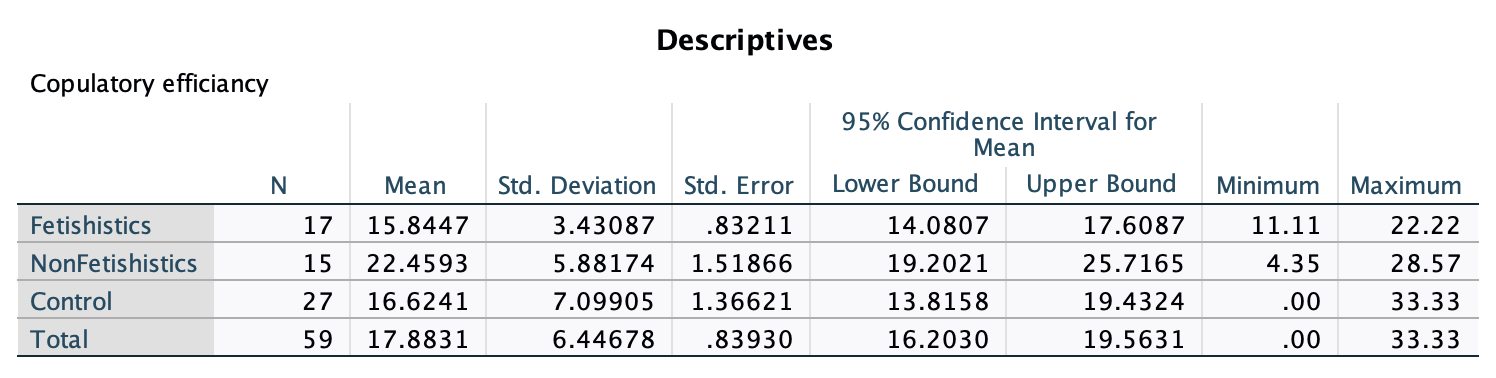
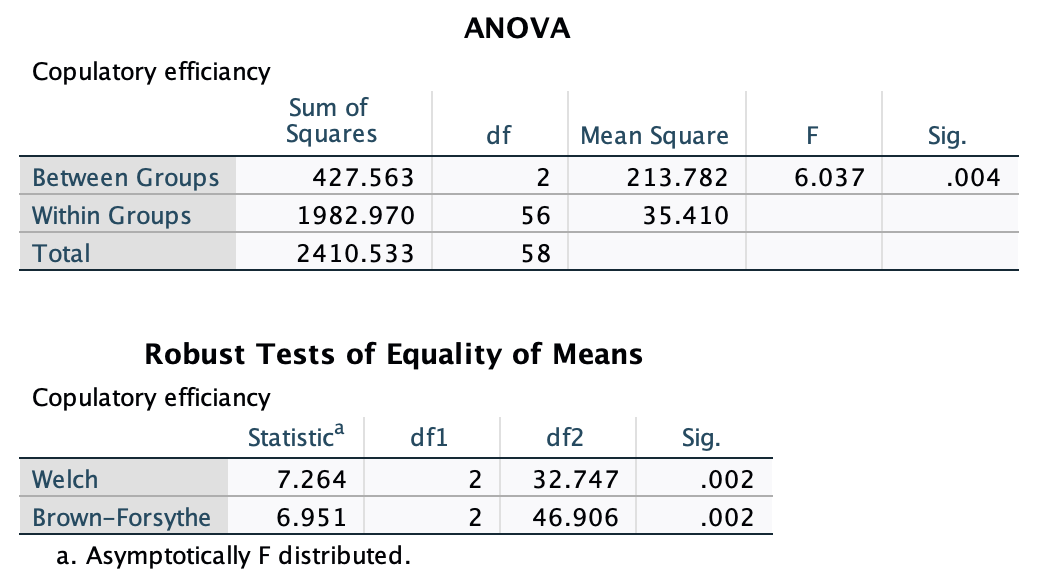
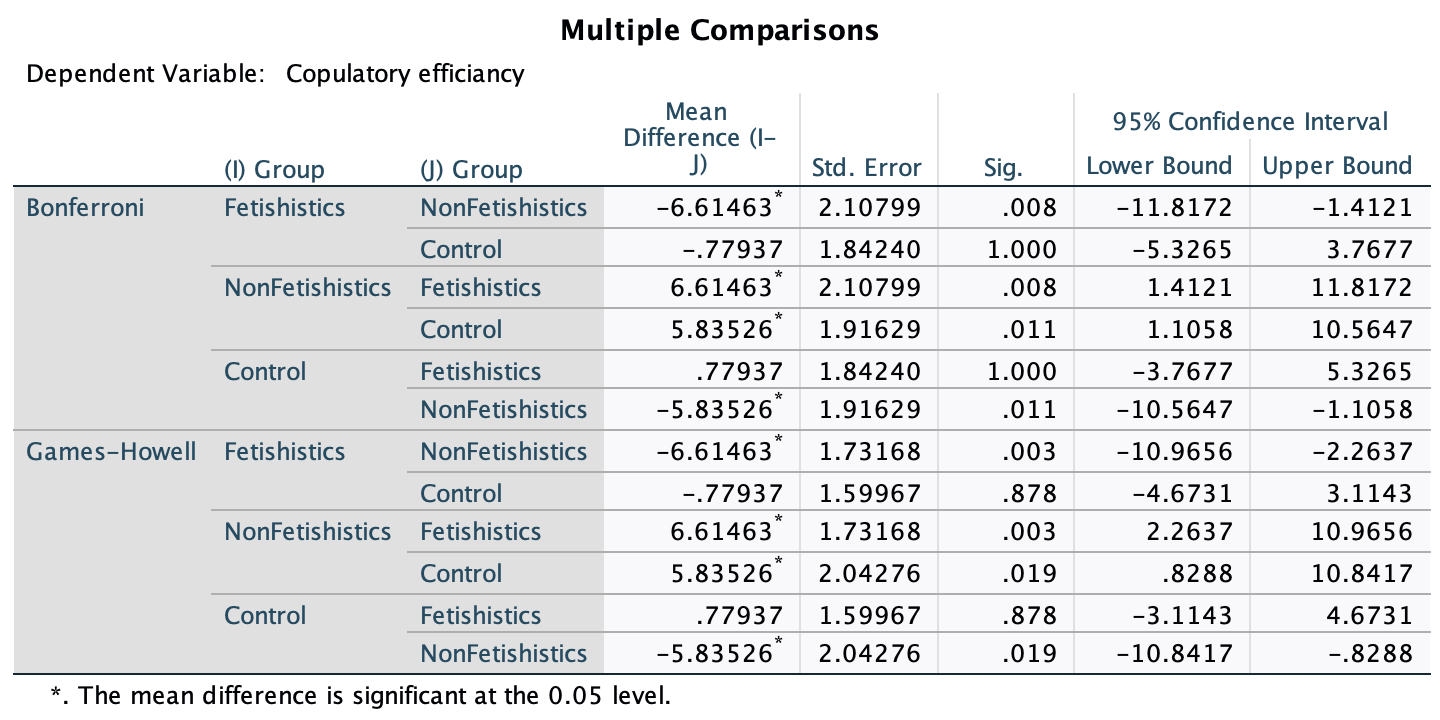
Task 12.9
A sociologist wanted to compare murder rates (
murder) recorded in each month in a year at three high-profile locations in London (street): Ruskin Avenue, Acacia Avenue and Rue Morgue. Fit a robust model with bootstrapping to see in which streets the most murders happened. The data are inmurder.sav.
Looking at the means (Figure 231) we can see that Rue Morgue had the highest mean number of murders (M = 2.92) and Ruskin Avenue had the smallest mean number of murders (M = 0.83). These means will be important in interpreting the post hoc tests later. Figure 232 shows us the F-statistic for predicting mean murders from location. We should routinely look at the robust Fs. Let’s assume we’re using \(\alpha\) = 0.05. For all tests, because the observed significance value is less than 0.05 we can say that there was a significant effect of street on the number of murders. However, at this stage we still do not know exactly which streets had significantly more murders (we don’t know which groups differed).
Because there were no specific hypotheses I carried out post hoc tests and stuck to my favourite Games–Howell procedure (because variances were unequal).Each street is compared to all of the remaining streets (Figure 233). If we look at the values in the column labelled Sig. we can see that the only significant comparison was between Ruskin Avenue and Rue Morgue (p = 0.024); all other comparisons were non-significant because all the other values in this column are greater than 0.05. However, Acacia Avenue and Rue Morgue were close to being significantly different (p = 0.089). The question asked us to bootstrap the post hoc tests and this has been done. The columns of interest are the ones containing the BCa 95% confidence intervals (lower and upper limits). We can see that the difference between Ruskin Avenue and Rue Morgue remains significant after bootstrapping the confidence intervals; we can tell this because the confidence intervals do not cross zero for this comparison. Surprisingly, it appears that the difference between Acacia Avenue and Rue Morgue is now significant after bootstrapping the confidence intervals, because again the confidence intervals do not cross zero. This seems to contradict the p-values in the previous output; however, the p-value was close to being significant (p = 0.089). The mean values in the table of descriptives tell us that Rue Morgue had a significantly higher number of murders than Ruskin Avenue and Acacia Avenue; however, Acacia Avenue did not differ significantly in the number of murders compared to Ruskin Avenue.
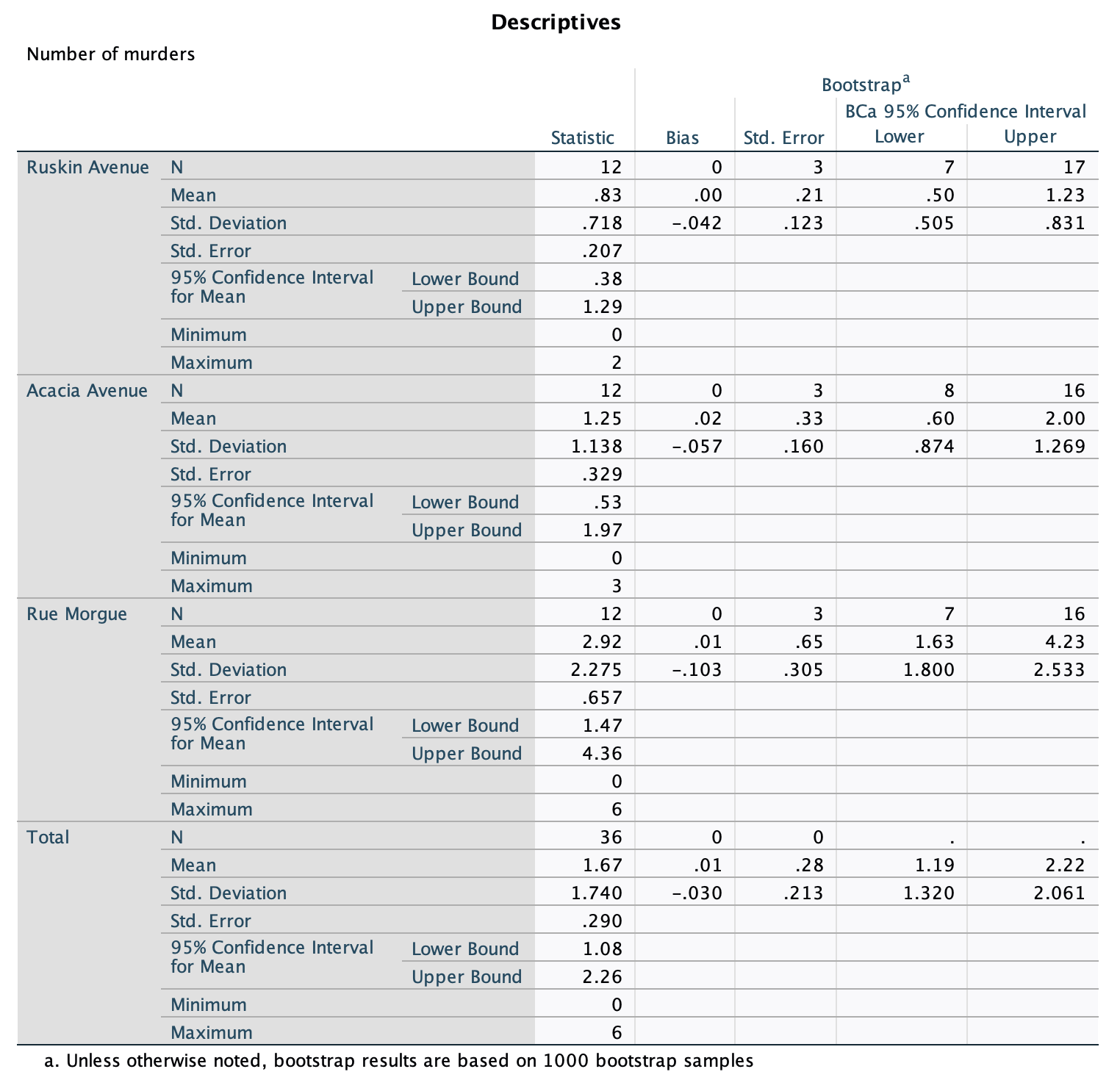
Chapter 13
Task 13.1
A few years back I was stalked. You’d think they could have found someone a bit more interesting to stalk, but apparently times were hard. It wasn’t particularly pleasant, but could have been a lot worse. I imagined a world in which a psychologist tried two different therapies on different groups of stalkers (25 stalkers in each group – this variable is called
therapy). To the first group he gave cruel-to-be-kind therapy (every time the stalkers followed him around, or sent him a letter, the psychologist attacked them with a cattle prod). The second therapy was psychodyshamic therapy, in which stalkers were hypnotized and regressed into their childhood to discuss their penis (or lack of penis), their dog’s penis, the seventh penis of a seventh penis, and any other penis that sprang to mind. The psychologist measured the number of hours stalking in one week both before (stalk_pre) and after (stalk_post) treatment (stalker.sav). Analyse the effect of therapy on stalking behaviour after therapy, adjusting for the amount of stalking behaviour before therapy.
First, conduct an ANOVA to test whether the number of hours spent stalking before therapy (our covariate) is independent of the type of therapy (our predictor variable). Your completed dialog box should look like Figure 236.
Figure 237 shows that the main effect of group is not significant, F(1, 48) = 0.06, p = 0.804, which shows that the average level of stalking behaviour before therapy was roughly the same in the two therapy groups. In other words, the mean number of hours spent stalking before therapy is not significantly different in the cruel-to-be-kind and psychodyshamic therapy groups. This result is good news for using this model to adjust for stalking behaviour before therapy.
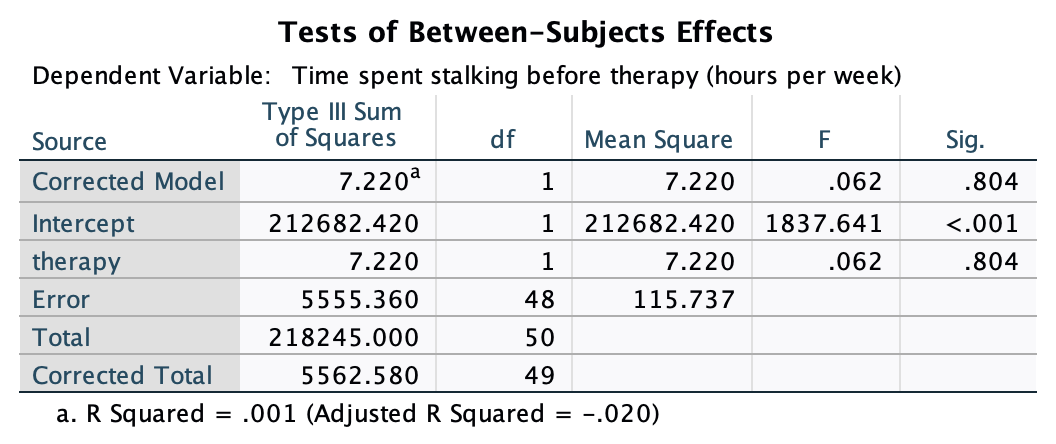
To conduct the ANCOVA, access the main dialog box and:
- Drag the outcome variable (
stalk_post) to the box labelled Dependent Variable. - Drag the predictor variable (
group) to the box labelled Fixed Factor(s). - Drag the covariate (
stalk_pre) to the box labelled Covariate(s).
Your completed dialog box should look like Figure 238. Click  and select the options in Figure 234, then click
and select the options in Figure 234, then click  and select the options in Figure 235.
and select the options in Figure 235.
Figure 239 shows that the covariate significantly predicts the outcome variable, so the hours spent stalking after therapy depend on the extent of the initial problem (i.e. the hours spent stalking before therapy). More interesting is that after adjusting for the effect of initial stalking behaviour, the effect of therapy is significant. To interpret the results of the main effect of therapy we look at the adjusted means, which tell us that stalking behaviour was significantly lower after the therapy involving the cattle prod than after psychodyshamic therapy (after adjusting for baseline stalking).
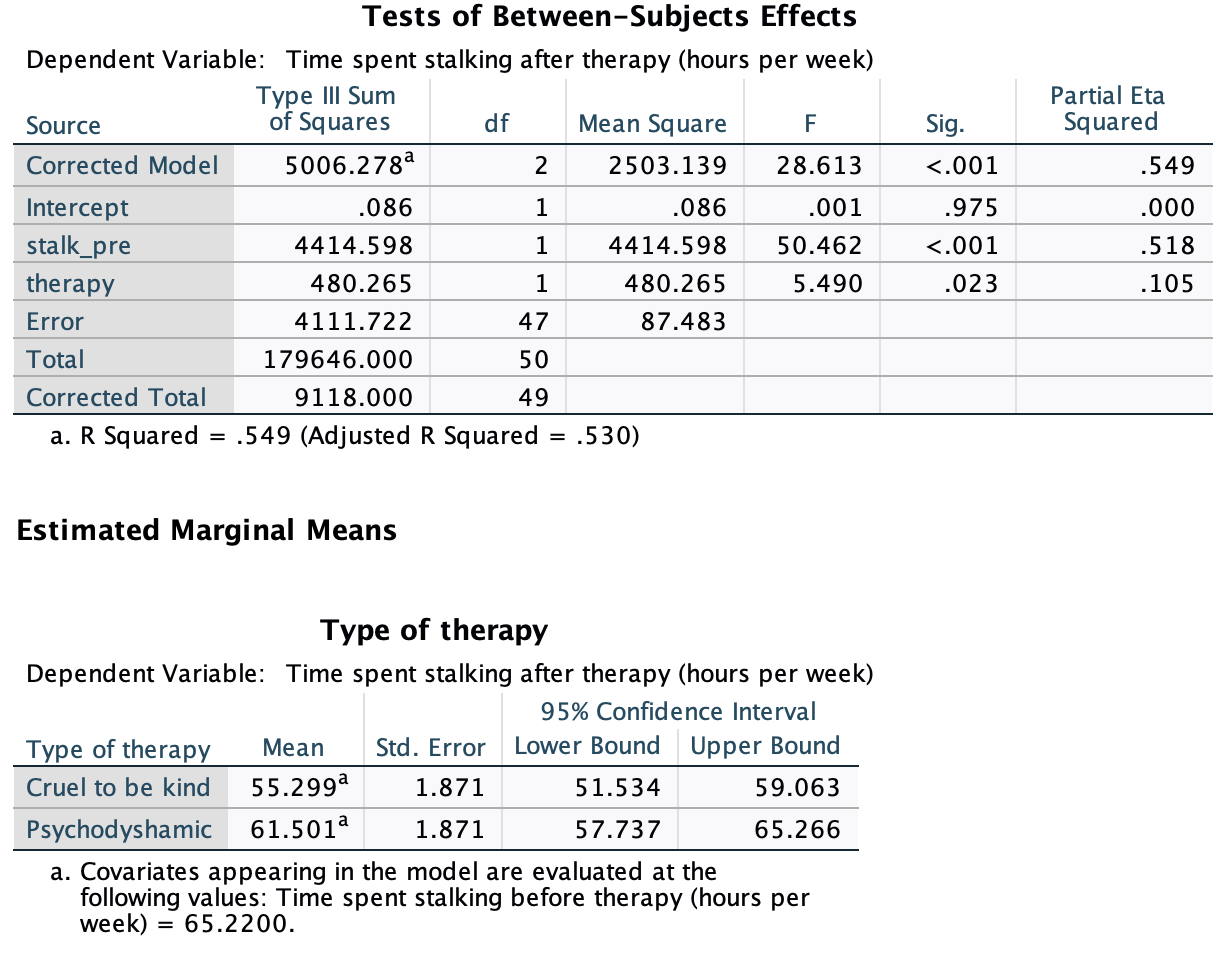
To interpret the covariate create a plot of the time spent stalking after therapy (outcome variable) and the initial level of stalking (covariate) using the chart builder (Figure 240). The resulting plot (Figure 241) shows that there is a positive relationship between the two variables: that is, high scores on one variable correspond to high scores on the other, whereas low scores on one variable correspond to low scores on the other.
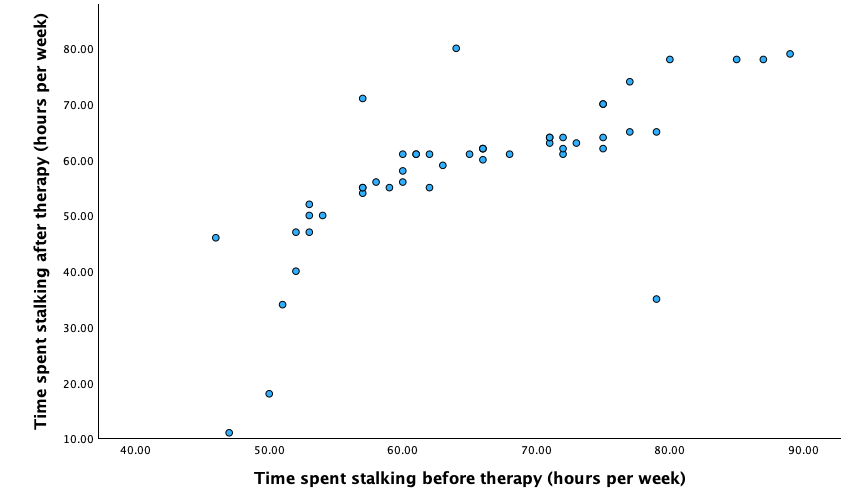
Task 13.2
Fit a robust model for Task 1.
We can fit this model using the following syntax
BEGIN PROGRAM R.
library(WRS2)
mySPSSdata = spssdata.GetDataFromSPSS(factorMode = "labels")
ancboot(stalk_post ~ therapy + stalk_pre, data = mySPSSdata, tr = 0.2, nboot = 1000)
END PROGRAM.The analysis identifies five values of stalk_pre (52, 57, 62, 66, and 72) for which the relationship between stalking pre-therapy and stalking post-therapy is comparable. At each of these design points, we’re told the number of cases for the two groups (\(n_1\) and \(n_2\)) that have a value of the covariate (stalk_pre) close to these design points. Based on these two samples, trimmed means (20% by default) are computed and the difference between them tested. This difference is stored in the column diff along with the boundaries of the associated 95% bootstrap confidence interval (corrected to control for doing five tests) in the next two columns. The test statistic comparing the difference is in the column statistic, with its p-value in the final column. There are no significant differences between trimmed means for any of the design points (all p-values are greater than 0.05).
Call:
ancboot(formula = stalk_post ~ therapy + stalk_pre, data = mySPSSdata,
tr = 0.2, nboot = 1000)
n1 n2 diff lower CI upper CI statistic p-value
stalk_pre = 52 13 12 -4.3472 -19.1749 10.4805 -0.8928 0.433
stalk_pre = 57 15 15 -5.0000 -16.8488 6.8488 -1.2851 0.246
stalk_pre = 62 20 18 -1.2500 -7.8564 5.3564 -0.5762 0.578
stalk_pre = 66 20 17 -1.2879 -6.8385 4.2627 -0.7066 0.493
stalk_pre = 72 17 12 -1.5682 -6.9781 3.8418 -0.8827 0.397Task 13.3
A marketing manager tested the benefit of soft drinks for curing hangovers. He took 15 people and got them drunk. The next morning as they awoke, dehydrated and feeling as though they’d licked a camel’s sandy feet clean with their tongue, he gave five of them water to drink, five of them Lucozade (a very nice glucose-based UK drink) and the remaining five a leading brand of cola (this variable is called
drink). He measured how well they felt (on a scale from 0 = I feel like death to 10 = I feel really full of beans and healthy) two hours later (this variable is calledwell). He measured howdrunkthe person got the night before on a scale of 0 = straight edge to 10 = flapping about like a haddock out of water (hangover.sav). Fit a model to see whether people felt better after different drinks when adjusting for how drunk they were the night before.
First let’s check that the predictor variable (drink) and the covariate (drunk) are independent. To do this we can run a one-way ANOVA. Your completed dialog box should look like Figure 242. Figure 243 shows that the main effect of drink is not significant, F(2, 12) = 1.36, p = 0.295, which shows that the average level of drunkenness the night before was roughly the same in the three drink groups. This result is good news for using this model to adjust for the variable drunk.
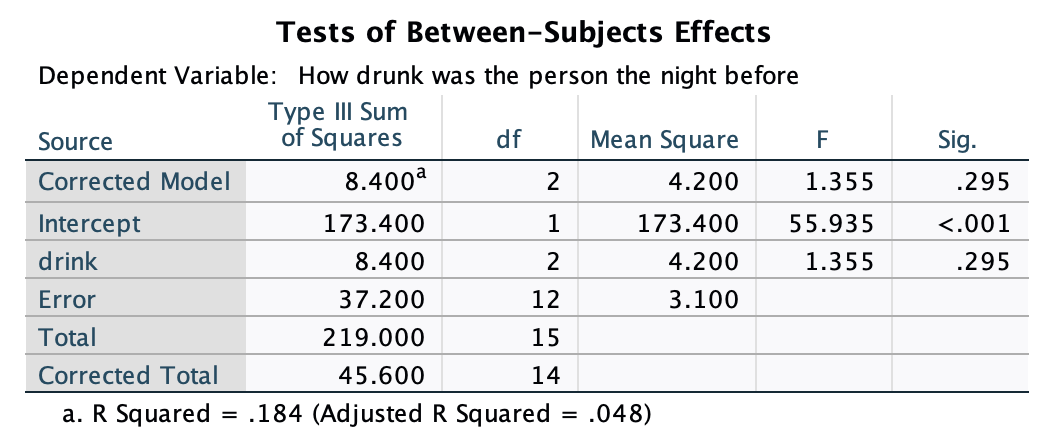
To conduct the ANCOVA, access the main dialog box and:
- Drag the outcome variable (
well) to the box labelled Dependent Variable. - Drag the predictor variable (
drink) to the box labelled Fixed Factor(s). - Drag the covariate (
drunk) to the box labelled Covariate(s).
Your completed dialog box should look like Figure 244. Click  and select the options in Figure 234 (for these data
and select the options in Figure 234 (for these data therapy in the image will be drink), then click  and select the options in Figure 235.
and select the options in Figure 235.
Click  to access the contrasts dialog box. In this example, a sensible set of contrasts would be simple contrasts comparing each experimental group with the control group, water. Select simple from the drop down list and specifying the first category as the reference category. The final dialog box should look like #fig-13_2d.
to access the contrasts dialog box. In this example, a sensible set of contrasts would be simple contrasts comparing each experimental group with the control group, water. Select simple from the drop down list and specifying the first category as the reference category. The final dialog box should look like #fig-13_2d.
Back in the main dialog box click  to fit the model.
to fit the model.
Figure 246 shows that the covariate significantly predicts the outcome variable, so the drunkenness of the person influenced how well they felt the next day. What’s more interesting is that after adjusting for the effect of drunkenness, the effect of drink is significant. The parameter estimates for the model (selected in the options dialog box) are computed having paramterized the variable drink using two dummy coding variables that compare each group against the last (the group coded with the highest value in the data editor, in this case the cola group). This reference category (labelled drink=3 in the output) is coded with a 0 for both dummy variables; drink=2 represents the difference between the group coded as 2 (Lucozade) and the reference category (cola); and drink=1 represents the difference between the group coded as 1 (water) and the reference category (cola). The beta values literally represent the differences between the means of these groups and so the significances of the t-tests tell us whether the group means differ significantly. From these estimates we could conclude that the cola and water groups have similar means whereas the cola and Lucozade groups have significantly different means.
The contrasts (Figure 247) compare level 2 (Lucozade) against level 1 (water) as a first comparison, and level 3 (cola) against level 1 (water) as a second comparison. These results show that the Lucozade group felt significantly better than the water group (contrast 1), but that the cola group did not differ significantly from the water group (p = 0.741). These results are consistent with the parameter estimates in (note that contrast 2 is identical to the regression parameters for drink=1 in the previous output).
The adjusted group means should be used for interpretation. The adjusted means (Figure 248) show that the significant difference between the water and the Lucozade groups reflects people feeling better in the Lucozade group (than the water group).
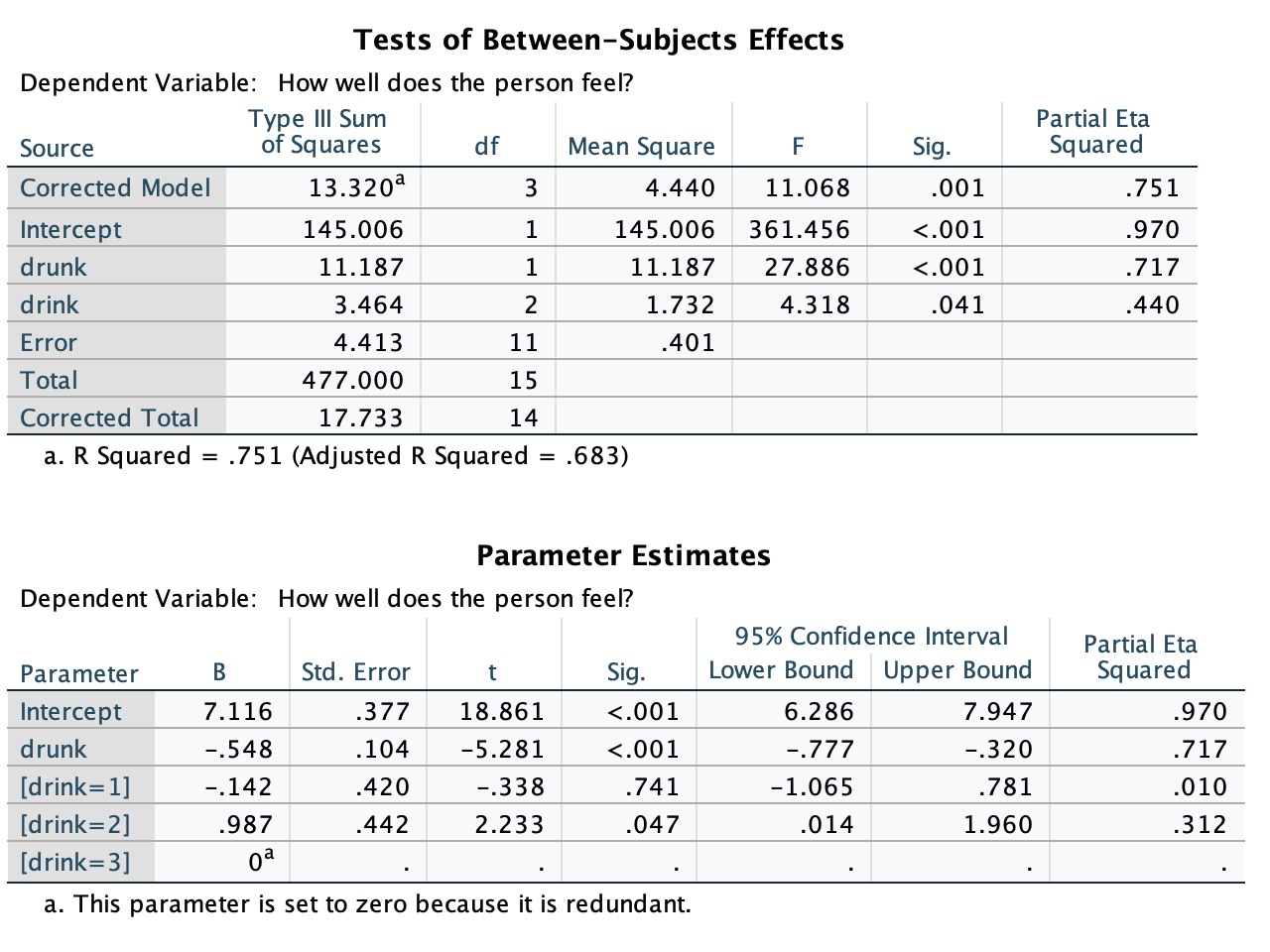
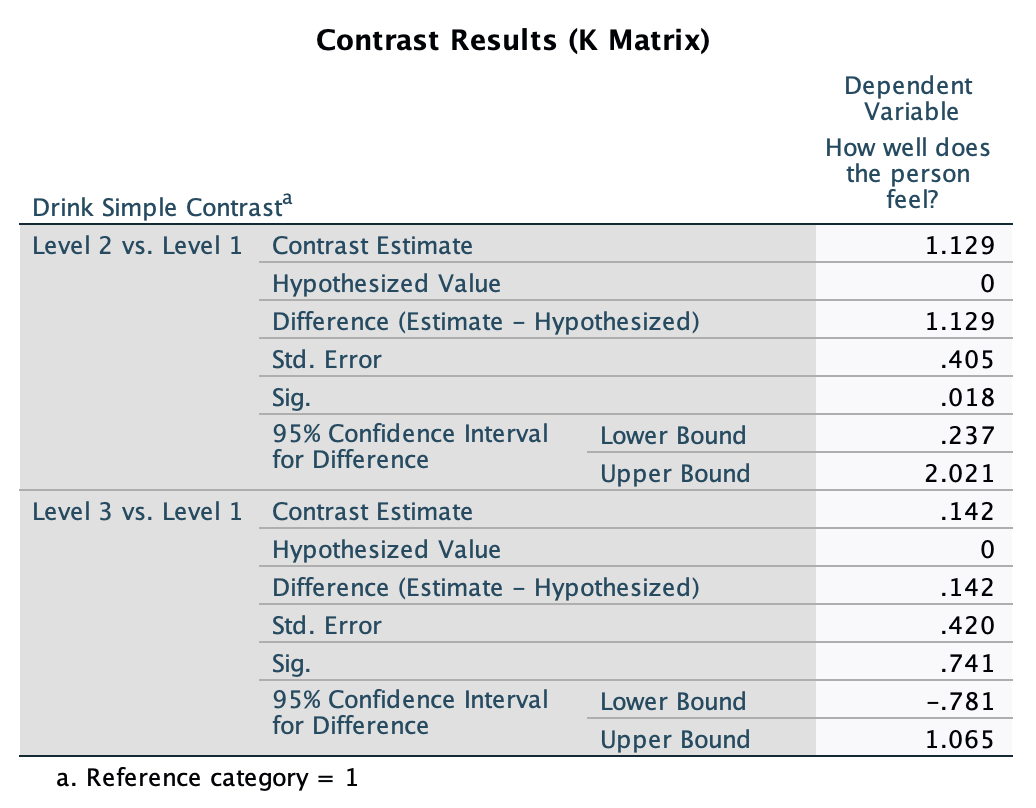
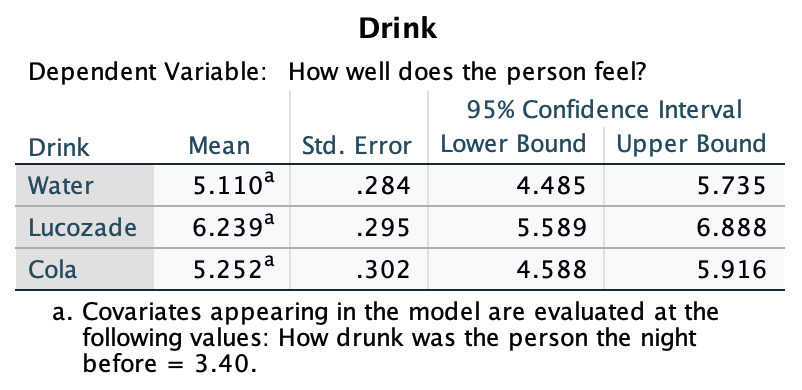
To interpret the covariate create a plot of the outcome (well, y-axis) against the covariate ( drunk, x-axis) using the chart builder (Figure 249). The resulting plot (Figure 250) shows that there is a negative relationship between the two variables: that is, high scores on one variable correspond to high scores on the other, whereas low scores on one variable correspond to low scores on the other. The more drunk you got, the less well you felt the following day.
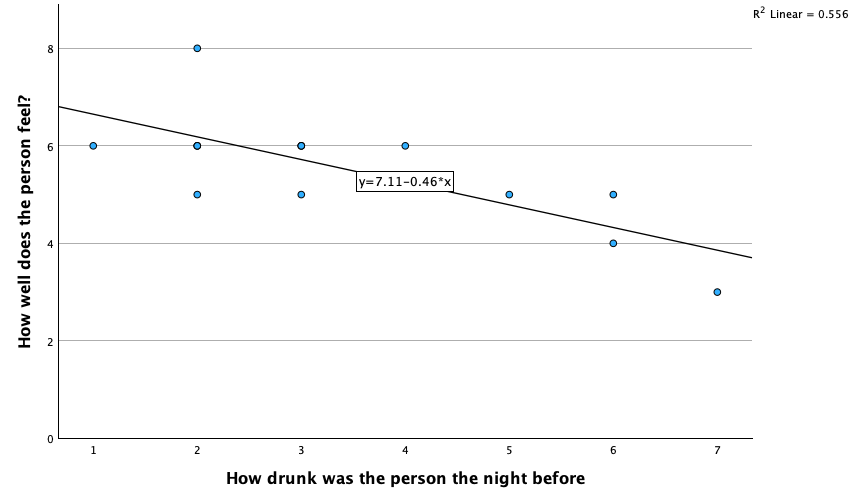
Task 13.4
Compute effect sizes for Task 3 and report the results.
The effect sizes for the main effect of drink can be calculated as follows:
\[ \begin{aligned} \eta_p^2 &= \frac{\text{SS}_\text{drink}}{\text{SS}_\text{drink} + \text{SS}_\text{residual}} \\ &= \frac{3.464}{3.464+4.413}\\ &= 0.44 \end{aligned} \]
And for the covariate:
\[ \begin{aligned} \eta_p^2 &= \frac{\text{SS}_\text{drunk}}{\text{SS}_\text{drunk} + \text{SS}_\text{residual}} \\ &= \frac{11.187}{11.187+4.413} \\ &= 0.72 \end{aligned} \]
We can get effect sizes for the model parameters from Figure 246.
Task 13.5
The highlight of the elephant calendar is the annual elephant soccer event in Nepal (google it). A heated argument burns between the African and Asian elephants. In 2010, the president of the Asian Elephant Football Association, an elephant named Boji, claimed that Asian elephants were more talented than their African counterparts. The head of the African Elephant Soccer Association, an elephant called Tunc, issued a press statement that read ‘I make it a matter of personal pride never to take seriously any remark made by something that looks like an enormous scrotum’. I was called in to settle things. I collected data from the two types of elephants (
elephant) over a season and recorded how many goals each elephant scored (goals) and how many years of experience the elephant had (experience). Analyse the effect of the type of elephant on goal scoring, covarying for the amount of football experience the elephant has (elephooty.sav).
First, let’s check that the predictor variable (elephant) and the covariate (experience) are independent. To do this we can run a one-way ANOVA. Your completed dialog box should look like Figure 251. Figure 252 shows that the main effect of elephant is not significant, F(1, 118) = 1.38, p = 0.24, which shows that the average level of prior football experience was roughly the same in the two elephant groups. This result is good news for using this model to adjust for the effects of experience.
To conduct the ANCOVA, access the main dialog box and:
- Drag the outcome variable (
goals) to the box labelled Dependent Variable. - Drag the predictor variable (
elephant) to the box labelled Fixed Factor(s). - Drag the covariate (
experience) to the box labelled Covariate(s).
Your completed dialog box should look like this Figure 253. Click  and select the options in Figure 234 (for these data
and select the options in Figure 234 (for these data therapy in the image will be elephant), then click  and select the options in Figure 235. Back in the main dialog box click
and select the options in Figure 235. Back in the main dialog box click  to fit the model.
to fit the model.
Figure 254 shows that the experience of the elephant significantly predicted how many goals they scored, F(1, 117) = 9.93, p = 0.002. After adjusting for the effect of experience, the effect of elephant is also significant. In other words, African and Asian elephants differed significantly in the number of goals they scored. The adjusted means tell us, specifically, that African elephants scored significantly more goals than Asian elephants after adjusting for prior experience, F(1, 117) = 8.59, p = 0.004.
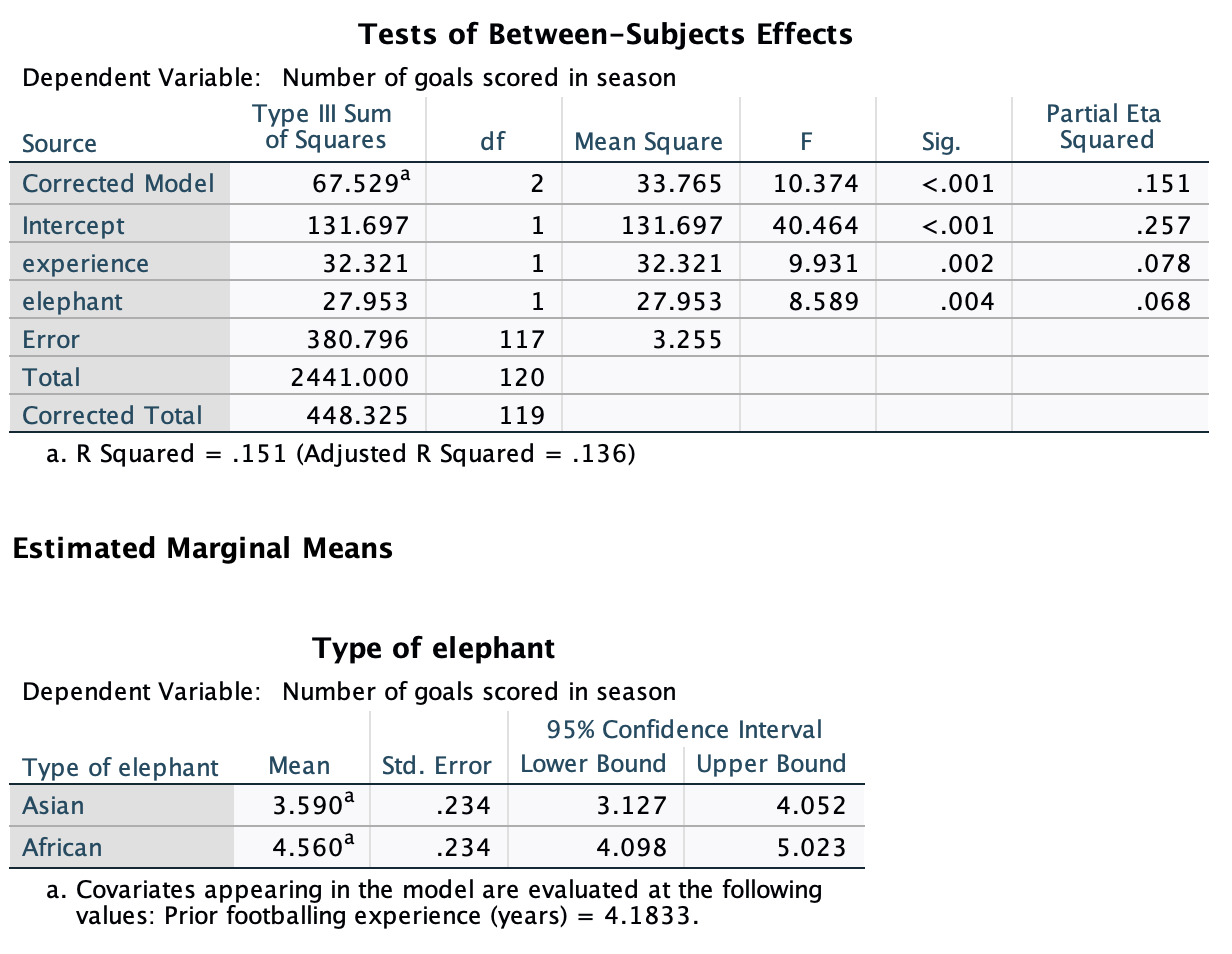
To interpret the covariate create a plot of the outcome (goals, y-axis) against the covariate ( experience, x-axis) using the chart builder (Figure 255). The resulting plot (Figure 256) shows that there is a (loose) positive relationship between the two variables that if you use your imagination looks like an elephant: the more prior football experience the elephant had, the more goals they scored in the season.
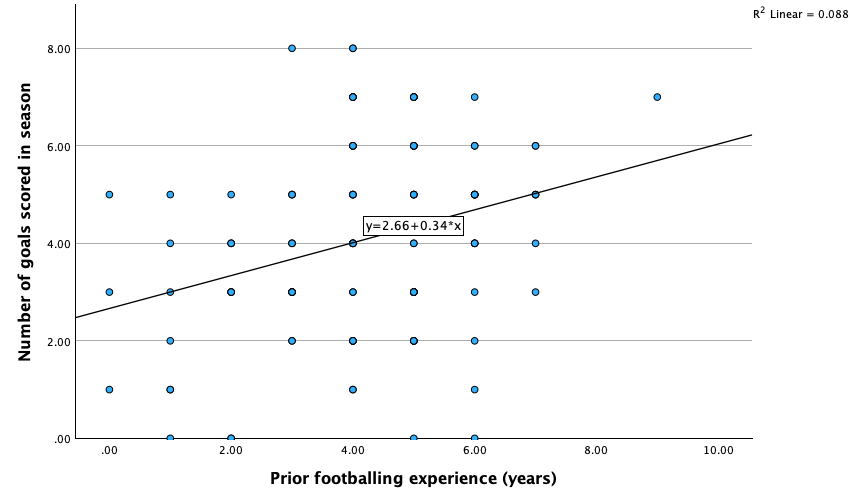
Task 13.6
In Chapter 4 (Task 6) we looked at data from people who had fish or cats as pets and measured their life satisfaction and, also, how much they like animals (
pets.sav). Fit a model predicting life satisfaction from the type of pet a person had and their animal liking score (covariate).
First, check that the predictor variable (pet) and the covariate (animal) are independent. To do this we can run a one-way ANOVA. Your completed dialog box should look like Figure 257. Figure 258 shows that the main effect of wife is not significant, F(1, 18) = 0.06, p = 0.81, which shows that the average level of love of animals was roughly the same in the two type of animal wife groups. This result is good news for using this model to adjust for the effects of the love of animals.
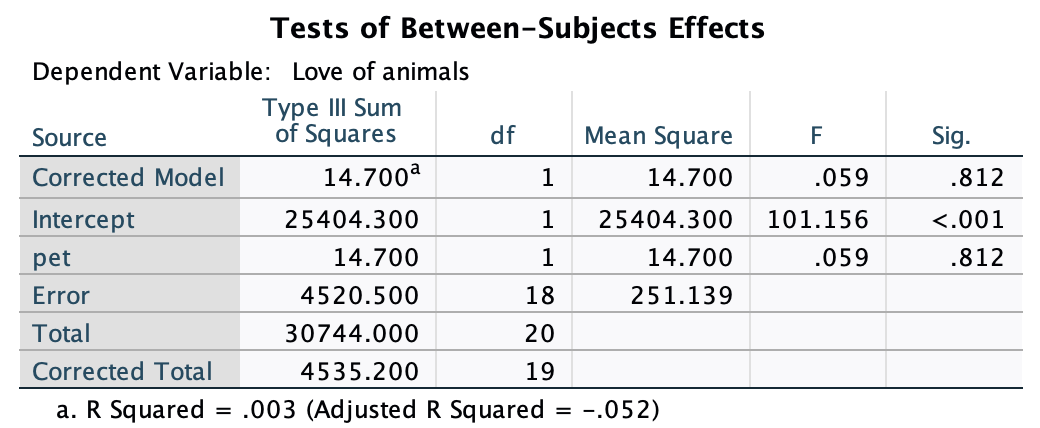
To conduct the ANCOVA, access the main dialog box and:
- Drag the outcome variable (
life_satisfaction) to the box labelled Dependent Variable. - Drag the predictor variable (
pet) to the box labelled Fixed Factor(s). - Drag the covariate (
animal) to the box labelled Covariate(s).
Your completed dialog box should look like Figure 259. Click  and select the options in Figure 234 (for these data
and select the options in Figure 234 (for these data therapy in the image will be pet), then click  and select the options in Figure 235. Back in the main dialog box click
and select the options in Figure 235. Back in the main dialog box click  to fit the model.
to fit the model.
Figure 260 shows that love of animals significantly predicted life satisfaction, F(1, 17) = 10.32, p = 0.005. After adjusting for the effect of love of animals, the effect of pet is also significant. In other words, life satisfaction differed significantly in those with cats as pets compared to those with fish. The adjusted means tell us, specifically, that life satisfaction was significantly higher in those who owned a cat, F(1, 17) = 16.45, p = 0.001.
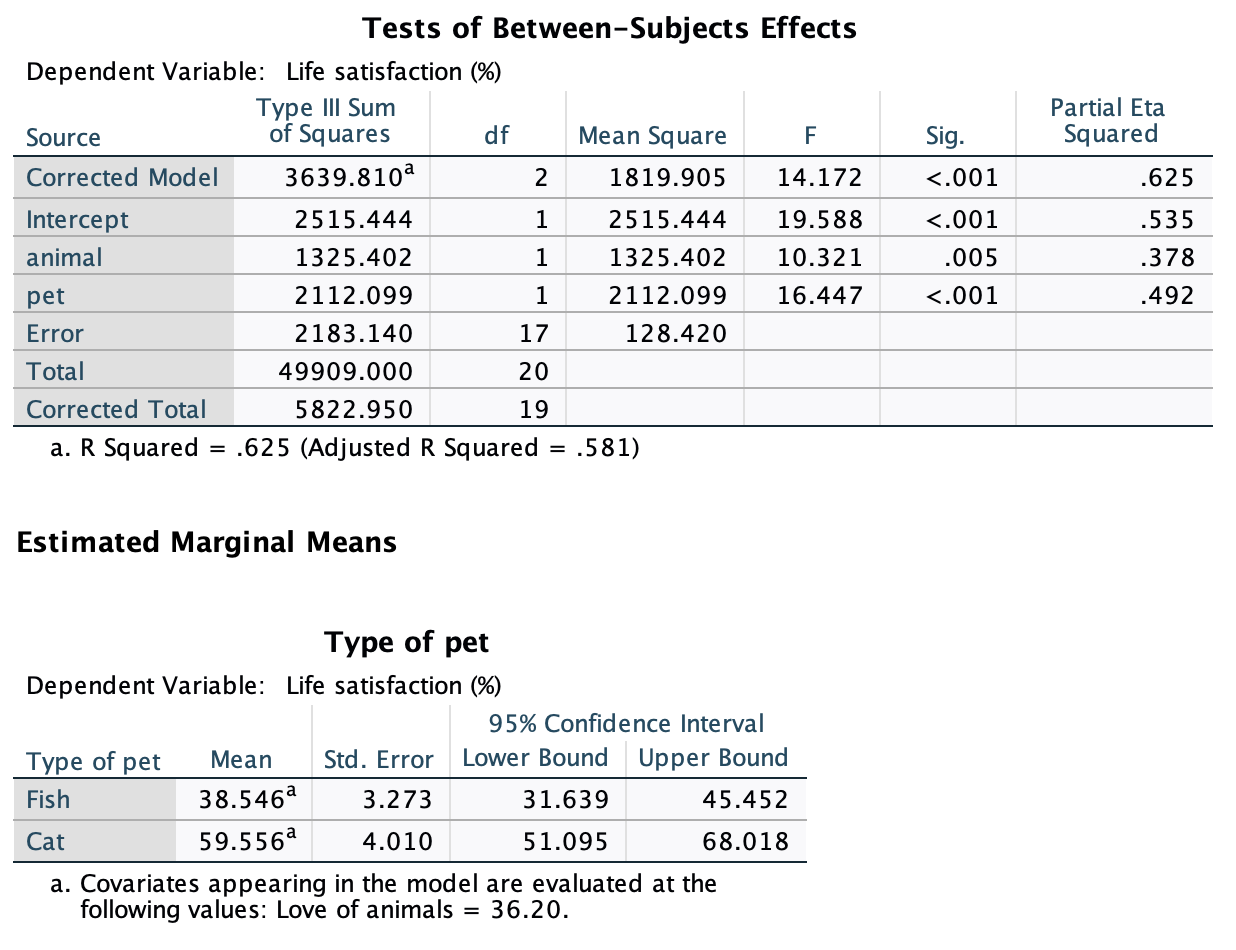
To interpret the covariate create a plot of the outcome (life_satisfaction, y-axis) against the covariate ( animal, x-axis) using the chart builder (Figure 261). The resulting plot (Figure 262) shows that there is a positive relationship between the two variables: the greater ones love of animals, the greater ones life satisfaction.
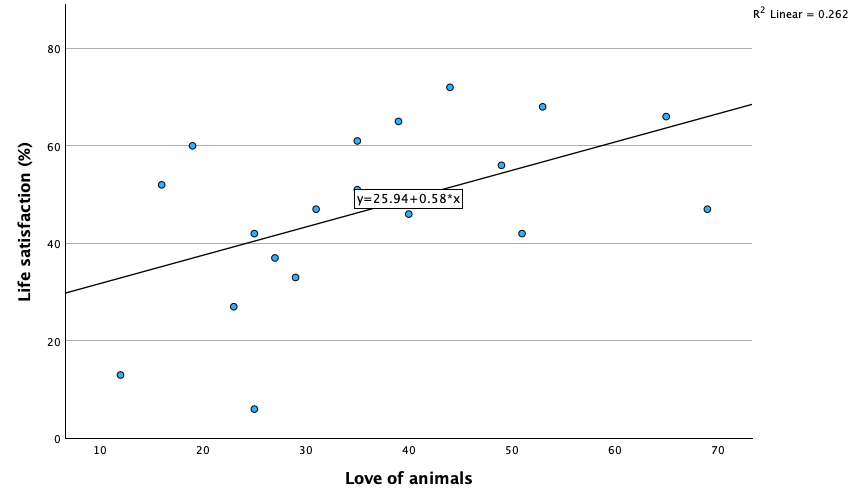
Task 13.7
Compare your results for Task 6 to those for the corresponding task in Chapter 11. What differences do you notice and why?
Well, this is awkward. I deleted the corresponding task in Chapter 11 because of moving some material out of that chapter. Oh, well, this task should have been re-phrased as:
Fit a linear model predicting life satisfaction from the type of pet and the effect of love of animals using what you learnt in Chapter 9. Compare this model to your results for Task 6. What differences do you notice and why?
To fit the linear model, access the main dialog box by selecting Analyze > Regression > Linear ... then
- Drag the outcome variable (
life_satisfaction) to the box labelled Dependent. - Drag the predictor variables (
petandanimal) to the box labelled Independent(s).
Your completed dialog box should look like Figure 263. We’ll leave the default options for the purpose of this exercise. From Figure 264 we can see that both love of animals, t(17) = 3.21, p = 0.005, and type of pet, t(17) = 4.06, p = 0.001, significantly predicted life satisfaction. In other words, after adjusting for the effect of love of animals, type of pet significantly predicted life satisfaction.
Now, let’s look again at the output from Task 6 (above), in which we conducted an ANCOVA predicting life satisfaction from the type of animal to which a person was married and their animal liking score (covariate). This output is in Figure 260.
The covariate, love of animals, was significantly related to life satisfaction, F(1, 17) = 10.32, p = 0.005, \(\eta_p^2\) = 0.38. There was also a significant effect of the type of pet after adjusting for love of animals, F(1, 17) = 16.45, p < 0.001, \(\eta_p^2\) = 0.49, indicating that life satisfaction was significantly higher for people who had cats as pets (M = 59.56, SE = 4.01) than for those with fish (M = 38.55, SE = 3.27).
The conclusions are the same as from the linear model, but more than that:
- The p-values for both effects are identical.
- This is because there is a direct relationship between t and F. In fact \(F = t^2\). Let’s compare the ts and Fs of our two effects:
- For love of animals, when we ran the analysis as ‘regression’ we got t = 3.213 (Figure 264). If we square this value we get \(t^2 = 3.213^2 = 10.32\). This is the value of F that we got when we ran the model as ‘ANCOVA’ (Figure 260).
- for the type of pet, when we ran the analysis as ‘regression’ we got t = 4.055 (Figure 264). If we square this value we get \(t^2 = 4.055^2 = 16.44\). This is the value of F that we got when we ran the model as ‘ANCOVA’ (Figure 260).
Basically, this task is all about showing you that despite the menu structure in SPSS creating false distinctions between models, when you do ‘ANCOVA’ and ‘regression’ you are, in both cases, using the general linear model and accessing it via different menus.
Task 13.8
In Chapter 10 we compared the number of mischievous acts in people who had invisibility cloaks to those without (cloak). Imagine we replicated that study, but changed the design so that we recorded the number of mischievous acts in these participants before the study began (
mischief_pre) as well as during the study (mischief). Fit a model to see whether people with invisibility cloaks get up to more mischief than those without when factoring in their baseline level of mischief (invisibility_base.sav).
First, check that the predictor variable (cloak) and the covariate (mischief1) are independent. To do this we can run a one-way ANOVA. Your completed dialog box should look like Figure 265. Figure 266 shows that the main effect of cloak is not significant, F(1, 78) = 0.14, p = 0.71, which shows that the average level of baseline mischief was roughly the same in the two cloak groups. This result is good news for using this model to adjust for the effects of baseline mischief.
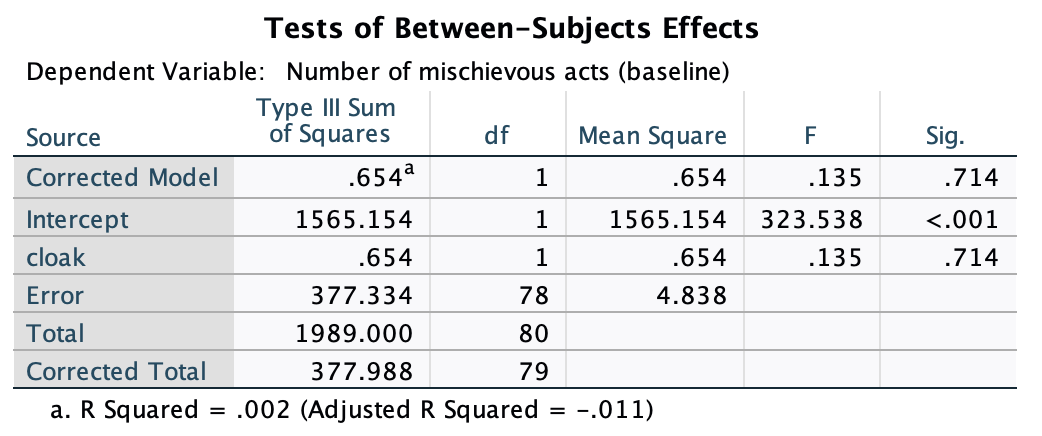
To conduct the ANCOVA, access the main dialog box and:
- Drag the outcome variable (
mischief_post) to the box labelled Dependent Variable. - Drag the predictor variable (
cloak) to the box labelled Fixed Factor(s). - Drag the covariate (
mischief_pre) to the box labelled Covariate(s).
Your completed dialog box should look like this Figure 267. Click  and select the options in Figure 234 (for these data
and select the options in Figure 234 (for these data therapy in the image will be cloak), then click  and select the options in Figure 235. Back in the main dialog box click
and select the options in Figure 235. Back in the main dialog box click  to fit the model.
to fit the model.
Figure 268 shows that baseline mischief significantly predicted post-intervention mischief, F(1, 77) = 7.40, p = 0.008. After adjusting for baseline mischief, the effect of cloak is also significant. In other words, mischief levels after the intervention differed significantly in those who had an invisibility cloak and those who did not. The adjusted means tell us, specifically, that mischief was significantly higher in those with invisibility cloaks, F(1, 77) = 11.33, p = 0.001.
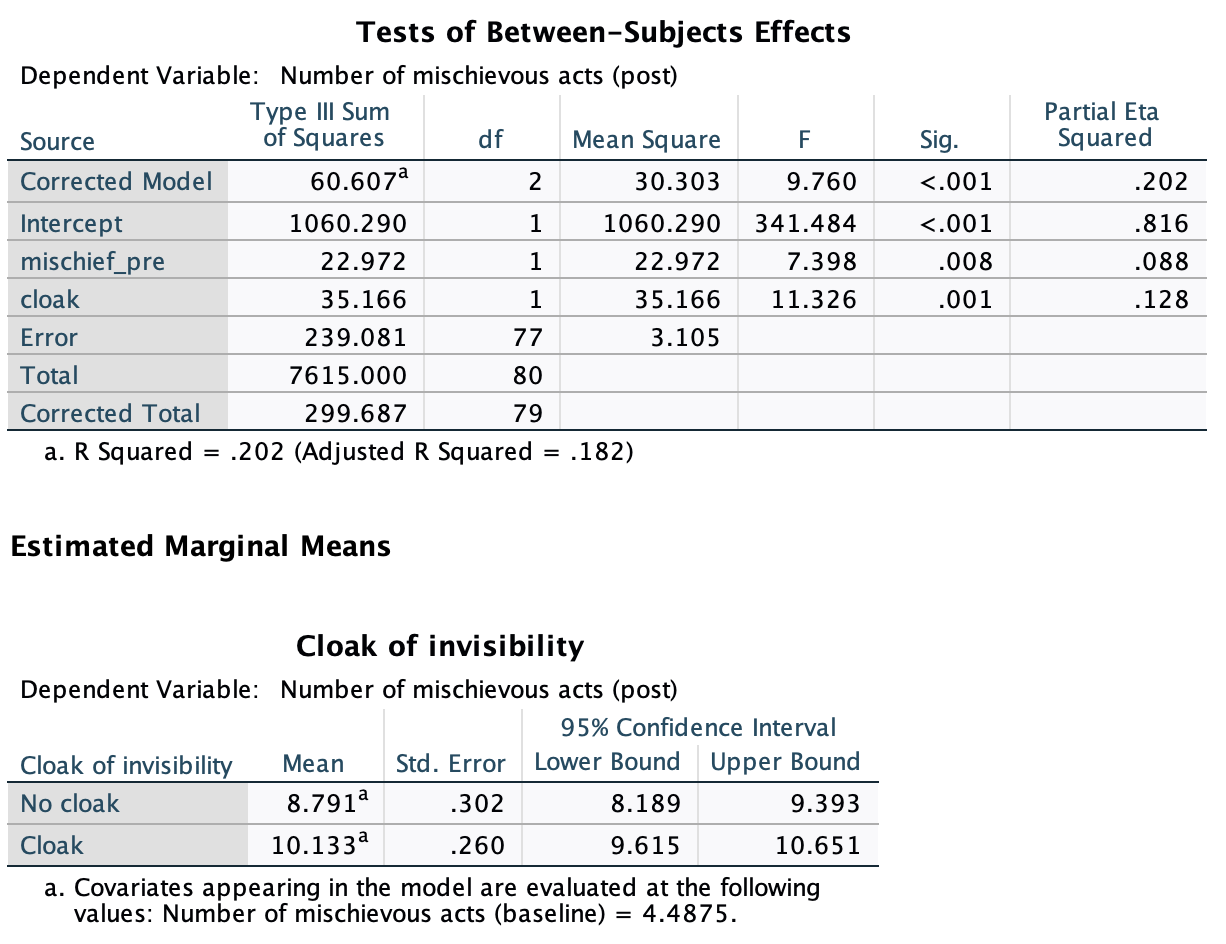
To interpret the covariate create a plot of the outcome (mischief_post, y-axis) against the covariate ( mischief_pre, x-axis) using the chart builder (Figure 269). The resulting plot (Figure 270) shows that there is a positive relationship between the two variables: the greater ones mischief levels before the cloaks were assigned to participants, the greater ones mischief after the cloaks were assigned to participants.
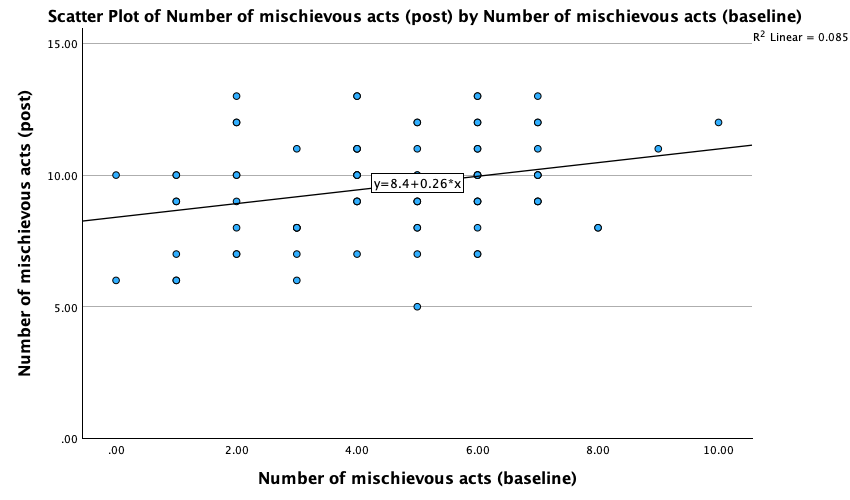
Chapter 14
Task 14.1
People have claimed that listening to heavy metal, because of its aggressive sonic palette and often violent or emotionally negative lyrics, leads to angry and aggressive behaviour (Selfhout et al., 2008). As a very non-violent metal fan this accusation bugs me. Imagine I designed a study to test this possibility. I took groups of self-classifying metalheads and non-metalheads (
fan) and assigned them randomly to listen to 15 minutes of either the sound of an angle grinder scraping a sheet of metal (control noise), metal music, or pop music (soundtrack). Each person rated theirangeron a scale ranging from 0 (‘All you need is love, da, da, da-da-da’) to 100 (‘All you wanna do is drag me down, all I wanna do is stamp you out’). Fit a model to test my idea (metal.sav).
To fit the model, follow the general procedure. Access the main dialog box and
- Drag the outcome variable (
anger) to the box labelled Dependent Variable. - Drag the predictor variables (
fanandsoundtrack) to the box labelled Fixed Factor(s).
Your completed dialog box should look like Figure 271. Click  and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click
and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click  and select the options in Figure 235 to get effect sizes and other useful information.
and select the options in Figure 235 to get effect sizes and other useful information.
Figure 273 shows that the main effect of music is significant, F(2, 84) = 116.82, p < .001, as is the interaction, F(2, 84) = 433.28, p < 0.001, but the main effect of whether someone was a metal music fan, F(1, 84) = 0.07, p = 0.788. Let’s look at these effects in turn by plotting the means in Figure 273.
The plot of the main effect of soundtrack shows that the significant effect is likely to reflect the fact that the sound of an angle grinder led to (on average) highest anger than pop or metal Figure 274. The table of post hoc tests (Figure 275) tells us more. First, anger was significantly higher after hearing an angle grinder compared to listening to both metal and pop (in both cases the value in the column labelled Sig. is less than 0.05). Levels of anger were statistically comparable after listening to pop and metal (p = 0.540).
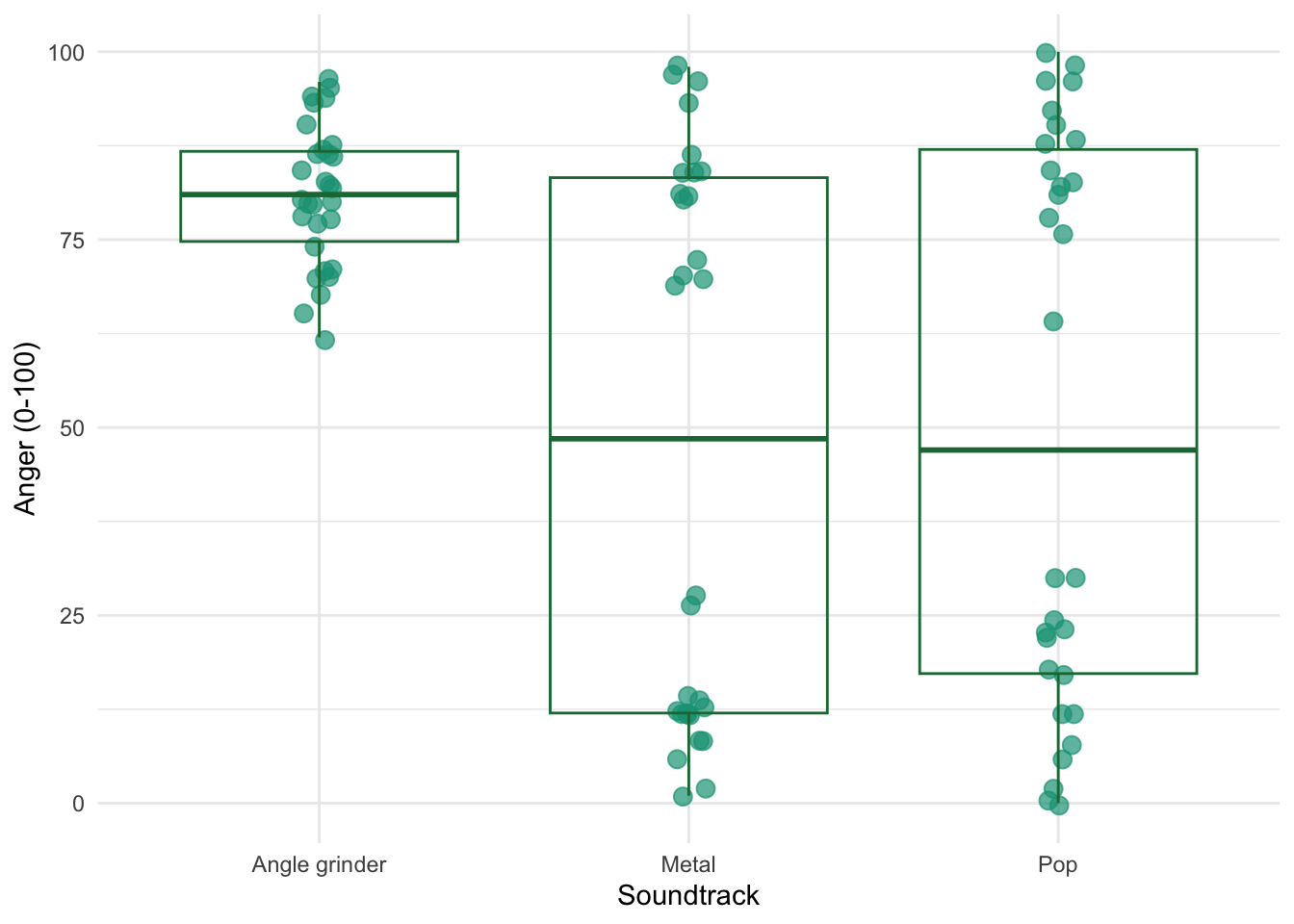
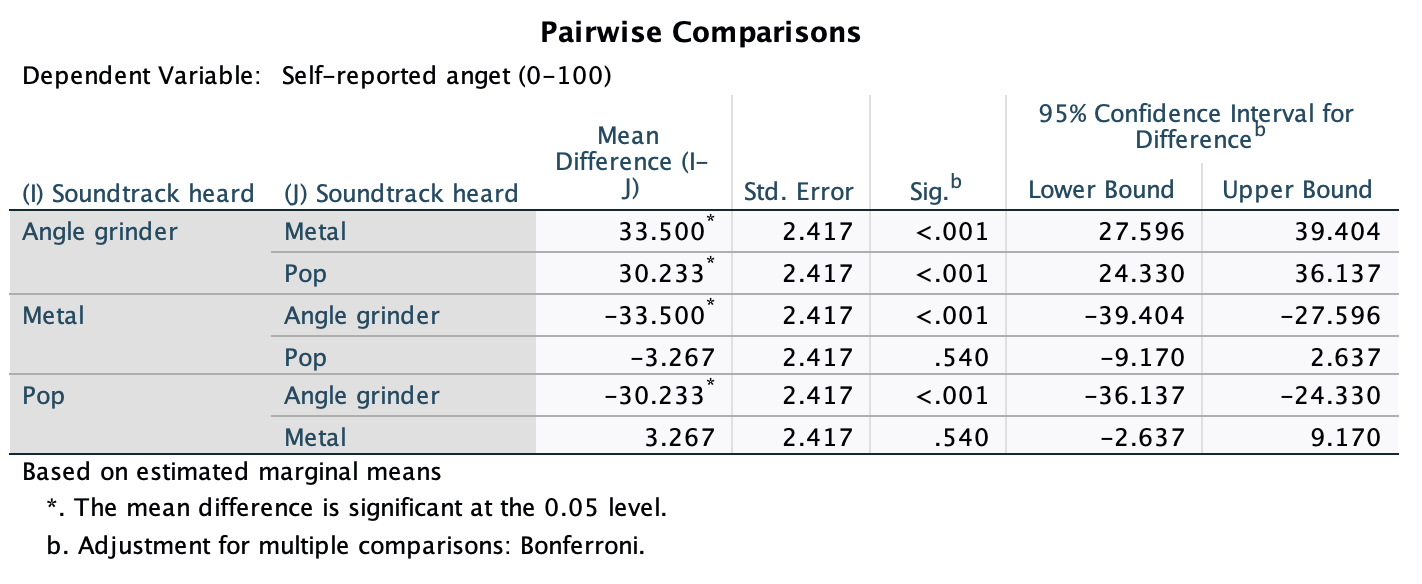
The main effect of fan was not significant, and the plot shows that when you ignore the type of soundtrack used, older people and younger people, on average, gave almost identical ratings (Figure 276).
The interaction effect is shown in Figure 277 along with the simple effects analysis in Figure 278. Three things stand out:
- Anger was high after listening to an angle grinder and this wasn’t significantly different for fans of metal and pop music, F(1, 84) = 0.30, p = 0.586.
- After listening to metal music anger was significantly lower for fans of metal music than for fans of pop music, F(1, 84) = 431.55, p < 0.001.
- After listening to pop music anger was significantly higher for fans of metal music than for fans of pop music, F(1, 84) = 434.79, p < 0.001.
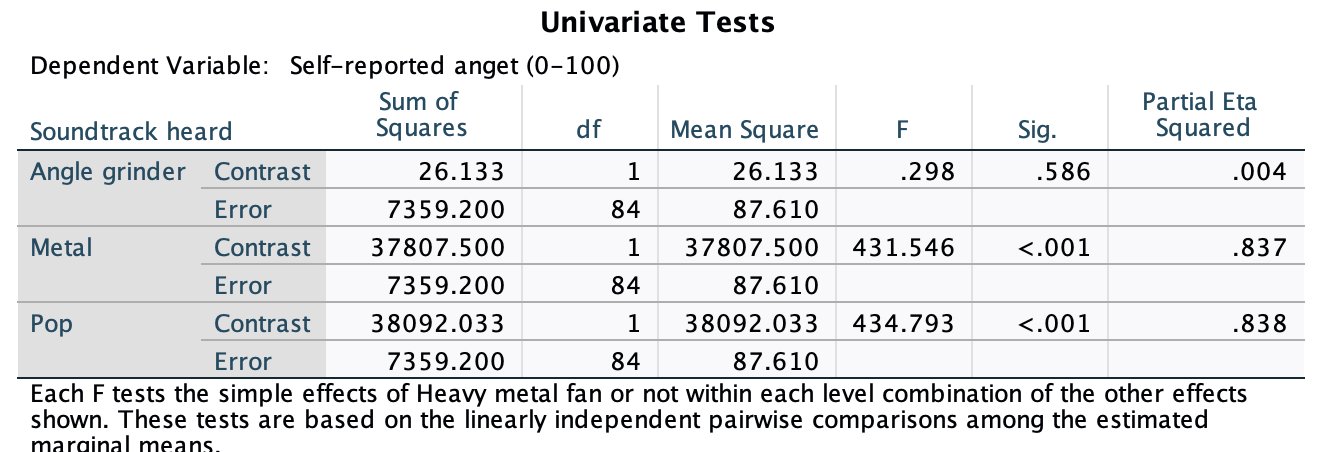
Task 14.2
Compute omega squared for the effects in Task 1 and report the results of the analysis.
First we use the mean squares and degrees of freedom in the summary table and the sample size per group to compute sigma for each effect:
\[ \begin{aligned} \hat{\sigma}_\text{sountrack}^2 &= \frac{(a-1)(\text{MS}_A-\text{MS}_\text{R})}{nab} = \frac{(3-1)(10234.878-87.61)}{15×3×2} = 8117.814 \\ \hat{\sigma}_\text{fan}^2 &= \frac{(b-1)(\text{MS}_B-\text{MS}_\text{R})}{nab} = \frac{(2-1)(6.40-87.61)}{15×3×2} = -64.968 \\ \hat{\sigma}_\text{interaction}^2 &= \frac{(a-1)(b-1)(\text{MS}_{A \times B}-\text{MS}_\text{R})}{nab} = \frac{(3-1)(2-1)(37959.633-87.61)}{15×3×2} = 30297.62 \\ \end{aligned} \]
We next need to estimate the total variability, and this is the sum of these other variables plus the residual mean squares:
\[ \begin{aligned} \hat{\sigma}_\text{total}^2 &= \hat{\sigma}_\text{soundtrack}^2 + \hat{\sigma}_\text{fan}^2 + \hat{\sigma}_\text{interaction}^2 + \text{MS}_\text{R} \\ &= 8117.814-64.968+30297.62+87.61 \\ &= 38438.08 \\ \end{aligned} \]
The effect size is then the variance estimate for the effect in which you’re interested divided by the total variance estimate:
\[ \omega_\text{effect}^2 = \frac{\hat{\sigma}_\text{effect}^2}{\hat{\sigma}_\text{total}^2} \]
For the main effect of soundtrack we get:
\[ \omega_\text{soundtrack}^2 = \frac{\hat{\sigma}_\text{soundtrack}^2}{\hat{\sigma}_\text{total}^2} = \frac{8117.814}{38438.08} = 0.211 \]
For the main effect of type of fan we get:
\[ \omega_\text{fan}^2 = \frac{\hat{\sigma}_\text{fan}^2}{\hat{\sigma}_\text{total}^2} = \frac{-64.968}{38438.08} = -0.002 \]
For the interaction of music and age we get:
\[ \omega_\text{interaction}^2 = \frac{\hat{\sigma}_\text{interaction}^2}{\hat{\sigma}_\text{total}^2} = \frac{30297.62}{38438.08} = 0.788 \]
We could report (remember if you’re using APA format to drop the leading zeros before p-values and \(\omega^2\), for example report p = .035 instead of p = 0.035):
Task 14.3
In Chapter 5 we used some data that related to male and female arousal levels when watching The Notebook or a documentary about notebooks (
notebook.sav). Fit a model to test whether men and women differ in their reactions to different types of films.
To fit the model, follow the general procedure. Access the main dialog box and
- Drag the outcome variable (
arousal) to the box labelled Dependent Variable. - Drag the predictor variables (
gender_identityandfilm) to the box labelled Fixed Factor(s).
Your completed dialog box should look like Figure 279 Click  and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click
and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click  and select the options in Figure 235 to get effect sizes and other useful information.
and select the options in Figure 235 to get effect sizes and other useful information.
The output shows that the main effect of gender_identity is significant, F(1, 36) = 7.292, p = 0.011, as is the main effect of film, F(1, 36) = 141.87, p < 0.001 and the interaction, F(1, 36) = 4.64, p = 0.038. Given that the interaction is significant we should focus on this effect (because it makes the main effects redundant). The interaction effect is shown in Figure 282 and the corresponding simple effects are in Figure 281. Psychological arousal is statistically comparable for those identifying as men and women during the documentary about notebooks (it is low for both sexes), F(1, 36) = 0.15, p = 0.702, \(\eta_p^2\) = 0.004. However, for the notebook those identifying as men experienced significantly greater psychological arousal than those identifying as women, F(1, 36) = 11.78, p = 0.002, \(\eta_p^2\) = 0.247.
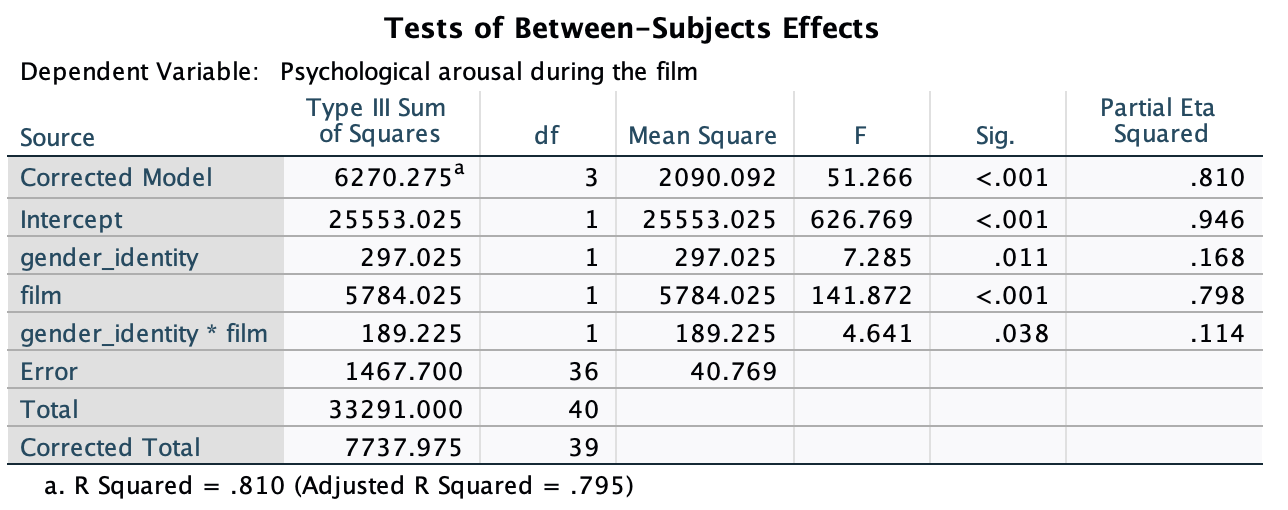
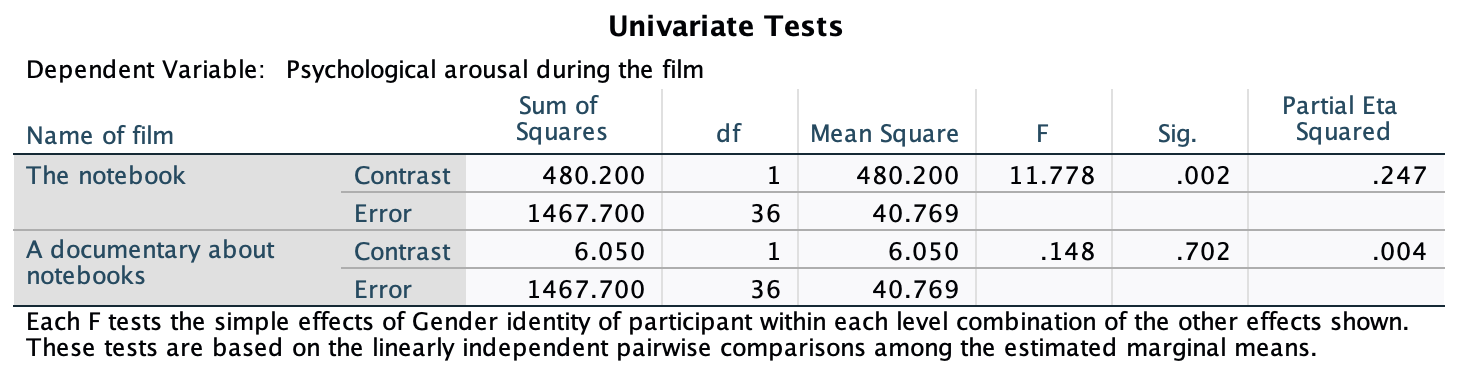
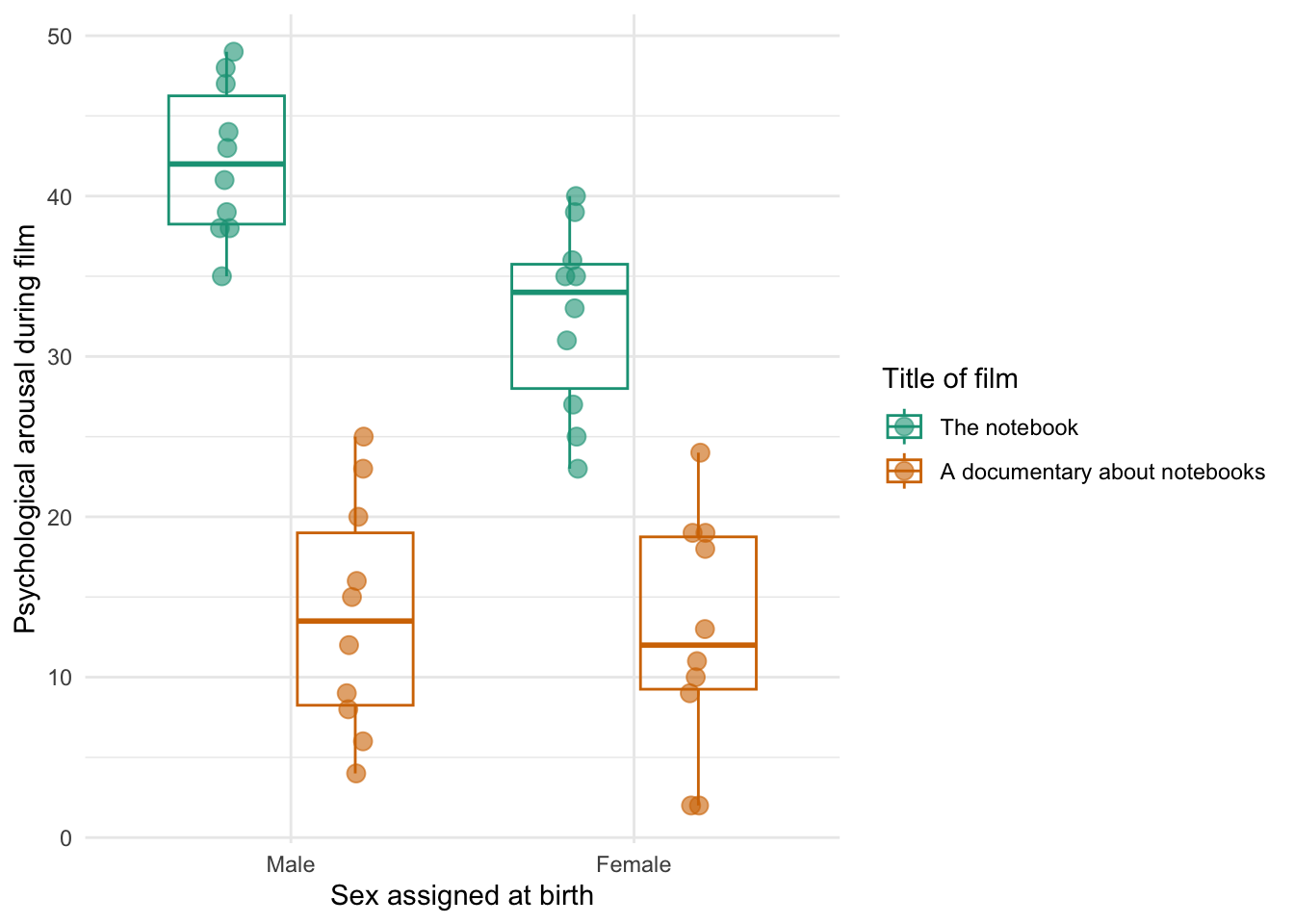
Task 14.4
Compute omega squared for the effects in Task 3 and report the results of the analysis.
First we use the mean squares and degrees of freedom in the summary table and the sample size per group to compute sigma for each effect:
\[ \begin{aligned} \hat{\sigma}_\alpha^2 &= \frac{(a-1)(\text{MS}_A-\text{MS}_\text{R})}{nab} = \frac{(2-1)(297.03-40.77)}{10×2×2} = 6.41 \\ \hat{\sigma}_\beta^2 &= \frac{(b-1)(\text{MS}_B-\text{MS}_\text{R})}{nab} = \frac{(2-1)(5784.03-40.77)}{10×2×2} = 143.58 \\ \hat{\sigma}_{\alpha\beta}^2 &= \frac{(a-1)(b-1)(\text{MS}_{A \times B}-\text{MS}_\text{R})}{nab} = \frac{(2-1)(2-1)(189.23-40.77)}{10×2×2} = 3.71 \\ \end{aligned} \]
We next need to estimate the total variability, and this is the sum of these other variables plus the residual mean squares:
\[ \begin{aligned} \hat{\sigma}_\text{total}^2 &= \hat{\sigma}_\alpha^2 + \hat{\sigma}_\beta^2 + \hat{\sigma}_{\alpha\beta}^2 + \text{MS}_\text{R} \\ &= 6.41+143.58+3.71+40.77 \\ &= 194.47 \\ \end{aligned} \]
The effect size is then the variance estimate for the effect in which you’re interested divided by the total variance estimate:
\[ \omega_\text{effect}^2 = \frac{\hat{\sigma}_\text{effect}^2}{\hat{\sigma}_\text{total}^2} \]
For the main effect of sex we get:
\[ \omega_\text{sex}^2 = \frac{\hat{\sigma}_\text{sex}^2}{\hat{\sigma}_\text{total}^2} = \frac{6.41}{194.47} = 0.03 \]
For the main effect of film we get:
\[ \omega_\text{film}^2 = \frac{\hat{\sigma}_\text{film}^2}{\hat{\sigma}_\text{total}^2} = \frac{143.58}{194.47} = 0.74 \]
For the interaction of sex and film we get:
\[ \omega_{\text{sex} \times \text{film}}^2 = \frac{\hat{\sigma}_{\text{sex} \times \text{film}}^2}{\hat{\sigma}_\text{total}^2} = \frac{3.71}{194.47} = 0.02 \]
We could report (remember if you’re using APA format to drop the leading zeros before p-values and \(\omega^2\), for example report p = .035 instead of p = 0.035):
Task 14.5
In Chapter 4 we used some data that related to learning in men and women when either reinforcement or punishment was used in teaching (
teaching.sav). Analyse these data to see whether men and women’s learning differs according to the teaching method used.
To fit the model, follow the general procedure. Access the main dialog box and
- Drag the outcome variable (
mark) to the box labelled Dependent Variable. - Drag the predictor variables (
sexandmethod) to the box labelled Fixed Factor(s).
Your completed dialog box should look like Figure 283 Click  and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click
and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click  and select the options in Figure 235 to get effect sizes and other useful information.
and select the options in Figure 235 to get effect sizes and other useful information.
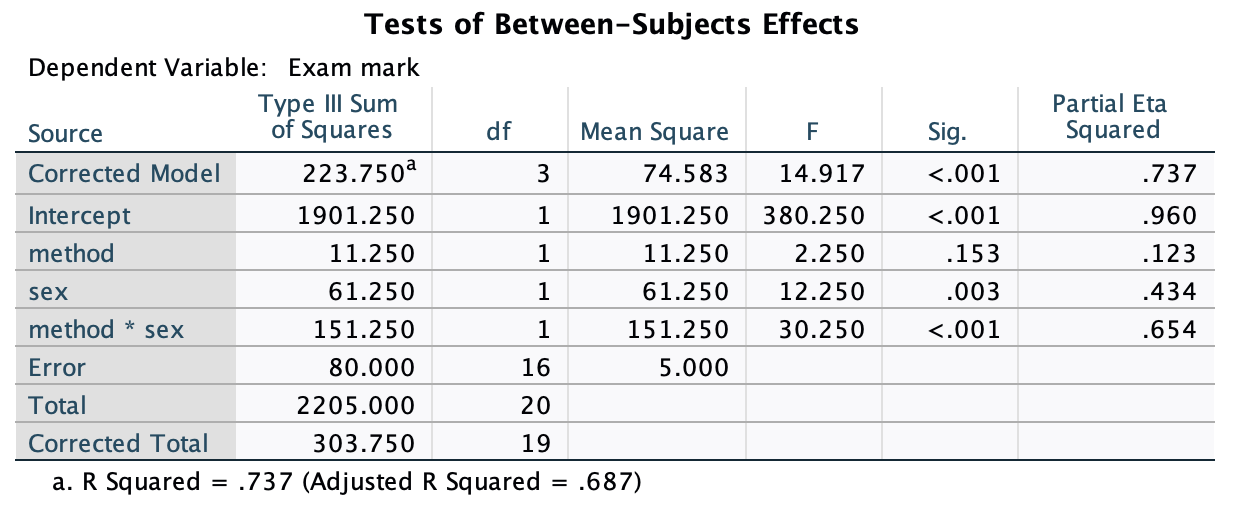
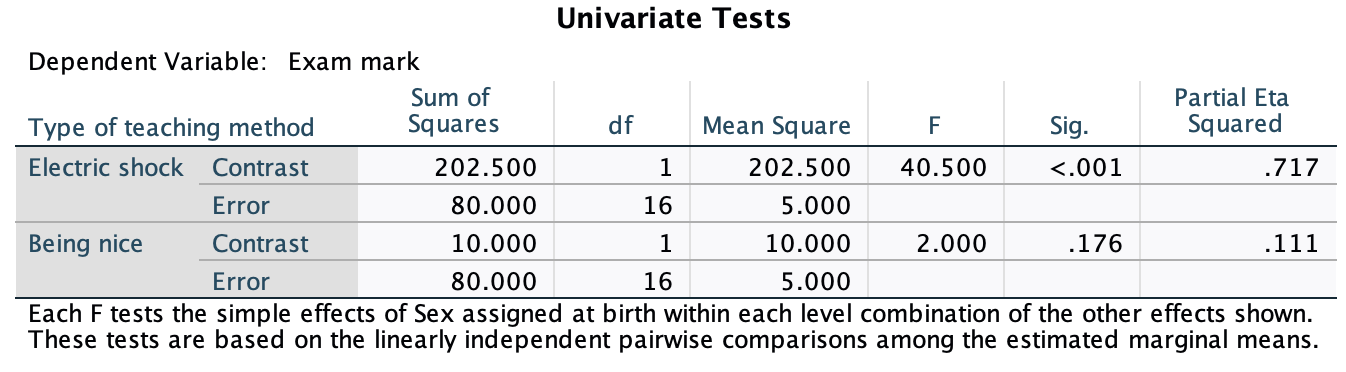
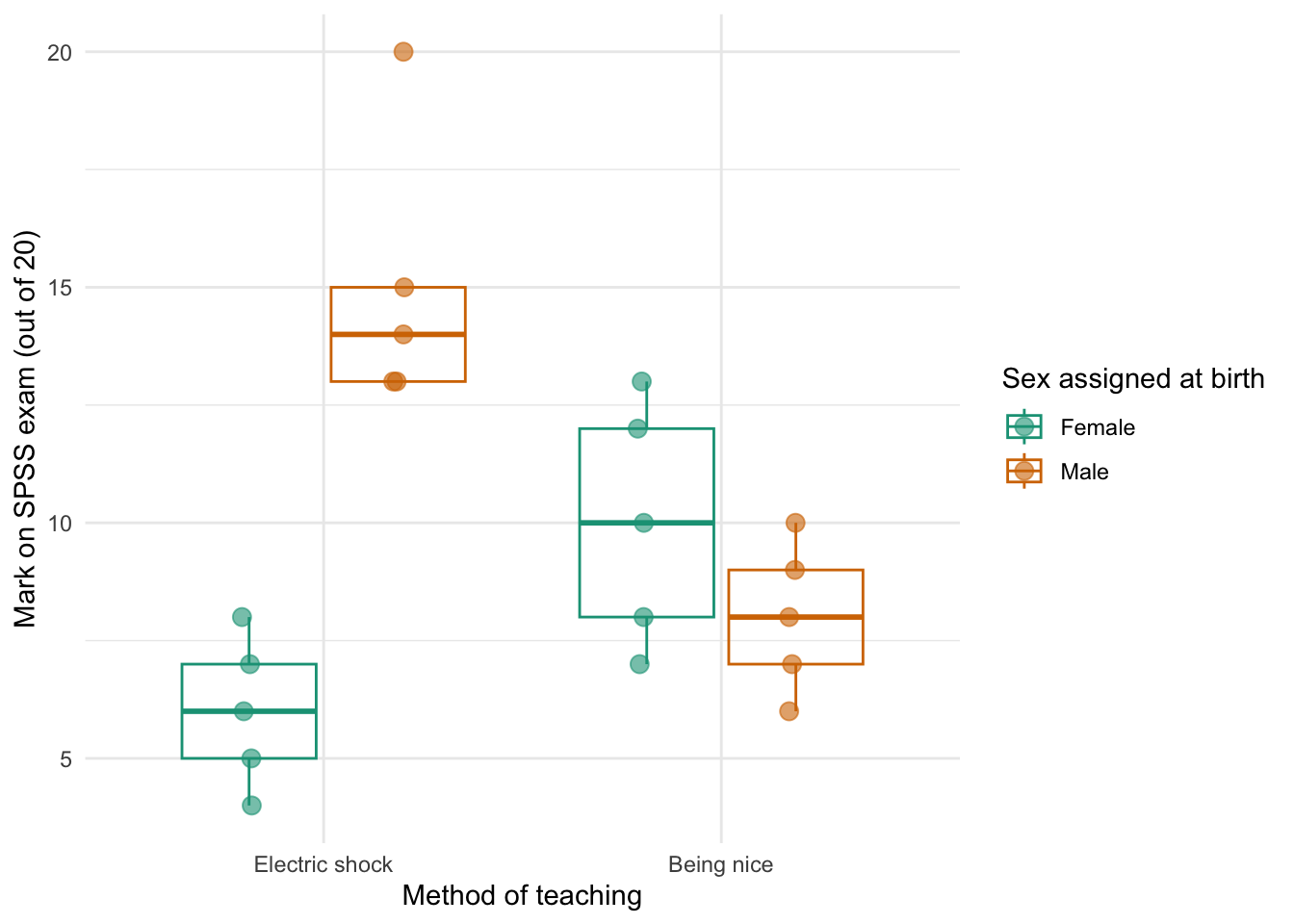
Task 14.6
At the start of this Chapter I described a way of empirically researching whether I wrote better songs than my old bandmate Malcolm, and whether this depended on the type of song (a symphony or song about flies). The outcome variable was the number of screams elicited by audience members during the songs. Plot the data and fit a model to test my hypothesis that the type of song moderates which songwriter is preferred (
escape.sav).
To produce the plot, access the chart builder and select a multiple line plot from the gallery. Then:
- Drag the outcome variable (
screams) to .
. - Drag one predictor variable (
song_type) to .
. - Drag the other predictor variable (
songwriter) to .
.
Your completed dialog box should look like Figure 287. In the Element Properties dialog box remember to select  to add error bars (#fig-14_6b). The resulting plot will look like Figure 289.
to add error bars (#fig-14_6b). The resulting plot will look like Figure 289.
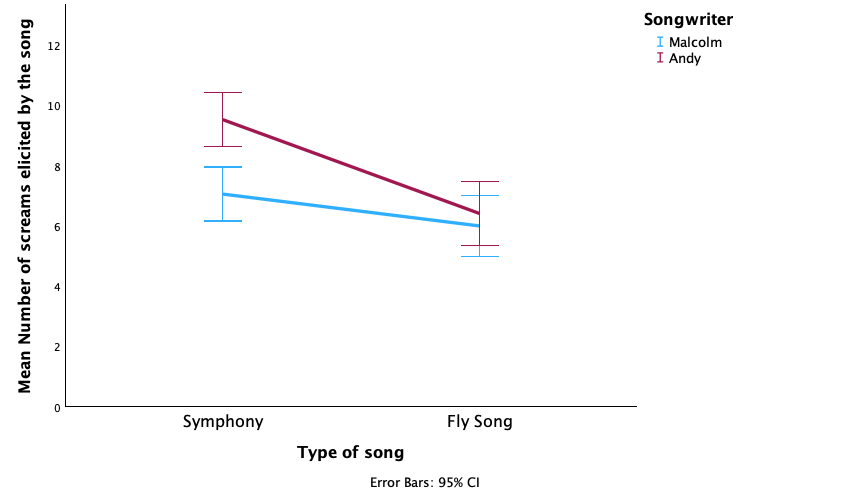
To fit the model, follow the general procedure. Access the main dialog box and
- Drag the outcome variable (
screams) to the box labelled Dependent Variable. - Drag the predictor variables (
song_typeandsongwriter) to the box labelled Fixed Factor(s).
Your completed dialog box should look like Figure 290. Click  and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click
and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click  and select the options in Figure 235 to get effect sizes and other useful information.
and select the options in Figure 235 to get effect sizes and other useful information.
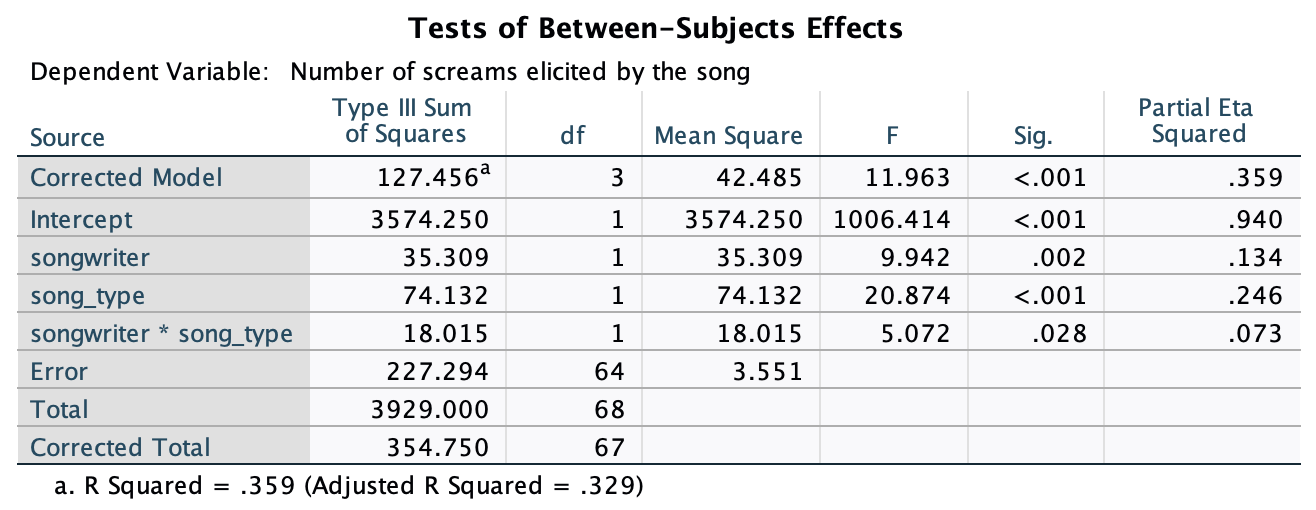
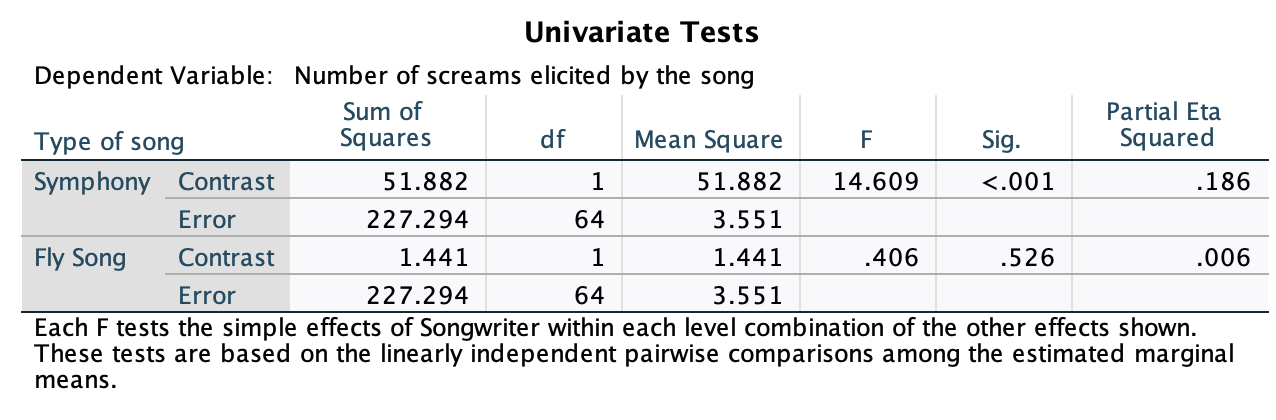
Task 14.7
Compute omega squared for the effects in Task 6 and report the results of the analysis.
First we use the mean squares and degrees of freedom in the summary table and the sample size per group to compute sigma for each effect:
\[ \begin{aligned} \hat{\sigma}_\alpha^2 &= \frac{(a-1)(\text{MS}_A-\text{MS}_\text{R})}{nab} = \frac{(2-1)(74.13-3.55)}{17×2×2} = 1.04 \\ \hat{\sigma}_\beta^2 &= \frac{(b-1)(\text{MS}_B-\text{MS}_\text{R})}{nab} = \frac{(2-1)(35.31-3.55)}{17×2×2} = 0.47 \\ \hat{\sigma}_{\alpha\beta}^2 &= \frac{(a-1)(b-1)(\text{MS}_{A \times B}-\text{MS}_\text{R})}{nab} = \frac{(2-1)(2-1)(18.02-3.77)}{17×2×2} = 0.21 \\ \end{aligned} \]
We next need to estimate the total variability, and this is the sum of these other variables plus the residual mean squares:
\[ \begin{aligned} \hat{\sigma}_\text{total}^2 &= \hat{\sigma}_\alpha^2 + \hat{\sigma}_\beta^2 + \hat{\sigma}_{\alpha\beta}^2 + \text{MS}_\text{R} \\ &= 1.04+0.47+0.21+3.77 \\ &= 5.49 \\ \end{aligned} \]
The effect size is then the variance estimate for the effect in which you’re interested divided by the total variance estimate:
\[ \omega_\text{effect}^2 = \frac{\hat{\sigma}_\text{effect}^2}{\hat{\sigma}_\text{total}^2} \]
For the main effect of type of song we get:
\[ \omega_\text{type of song}^2 = \frac{\hat{\sigma}_\text{type of song}^2}{\hat{\sigma}_\text{total}^2} = \frac{1.04}{5.49} = 0.19 \]
For the main effect of songwriter we get:
\[ \omega_\text{songwriter}^2 = \frac{\hat{\sigma}_\text{songwriter}^2}{\hat{\sigma}_\text{total}^2} = \frac{0.47}{5.49} = 0.09 \]
For the interaction of songwriter and type of song we get:
\[ \omega_{\text{songwriter} \times \text{type of song}}^2 = \frac{\hat{\sigma}_{\text{songwriter} \times \text{type of song}}^2}{\hat{\sigma}_\text{total}^2} = \frac{0.21}{5.49} = 0.04 \]
We could report (remember if you’re using APA format to drop the leading zeros before p-values and \(\omega^2\), for example report p = .035 instead of p = 0.035).
Task 14.8
There are reports of increases in injuries related to playing games consoles. These injuries were attributed mainly to muscle and tendon strains. A researcher hypothesized that a stretching warm-up before playing would help lower injuries, and that athletes would be less susceptible to injuries because their regular activity makes them more flexible. She took 60 athletes and 60 non-athletes (
athlete); half of them played on a Nintendo Switch and half watched others playing as a control (switch), and within these groups half did a 5-minute stretch routine before playing/watching whereas the other half did not (stretch). The outcome was a pain score out of 10 (where 0 is no pain, and 10 is severe pain) after playing for 4 hours (injury). Fit a model to test whether athletes are less prone to injury, and whether the prevention programme worked (switch.sav)
This design is a 2(Athlete: athlete vs. non-athlete) by 2(switch: playing switch vs. watching switch) by 2(Stretch: stretching vs. no stretching) three-way independent design. To fit the model, follow the general procedure. Access the main dialog box and
- Drag the outcome variable (
injury) to the box labelled Dependent Variable. - Drag the predictor variables (
athlete,switchandstretch) to the box labelled Fixed Factor(s).
Your completed dialog box should look like Figure 293 Click  and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click
and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click  and select the options in Figure 235 to get effect sizes and other useful information.
and select the options in Figure 235 to get effect sizes and other useful information.
The main summary table is in Figure 294 and Figure 295 shows simple effects analysis for the three-way interaction. Although the three-way interaction is significant and so supersedes all lower-order effects, we will look at each effect in turn to get some practice at interpretation.
There was a significant main effect of athlete, F(1, 112) = 64.82, p < .001, \(\eta_p^2\) = 0.37. Figure 296 shows that, on average, athletes had significantly lower injury scores than non-athletes.
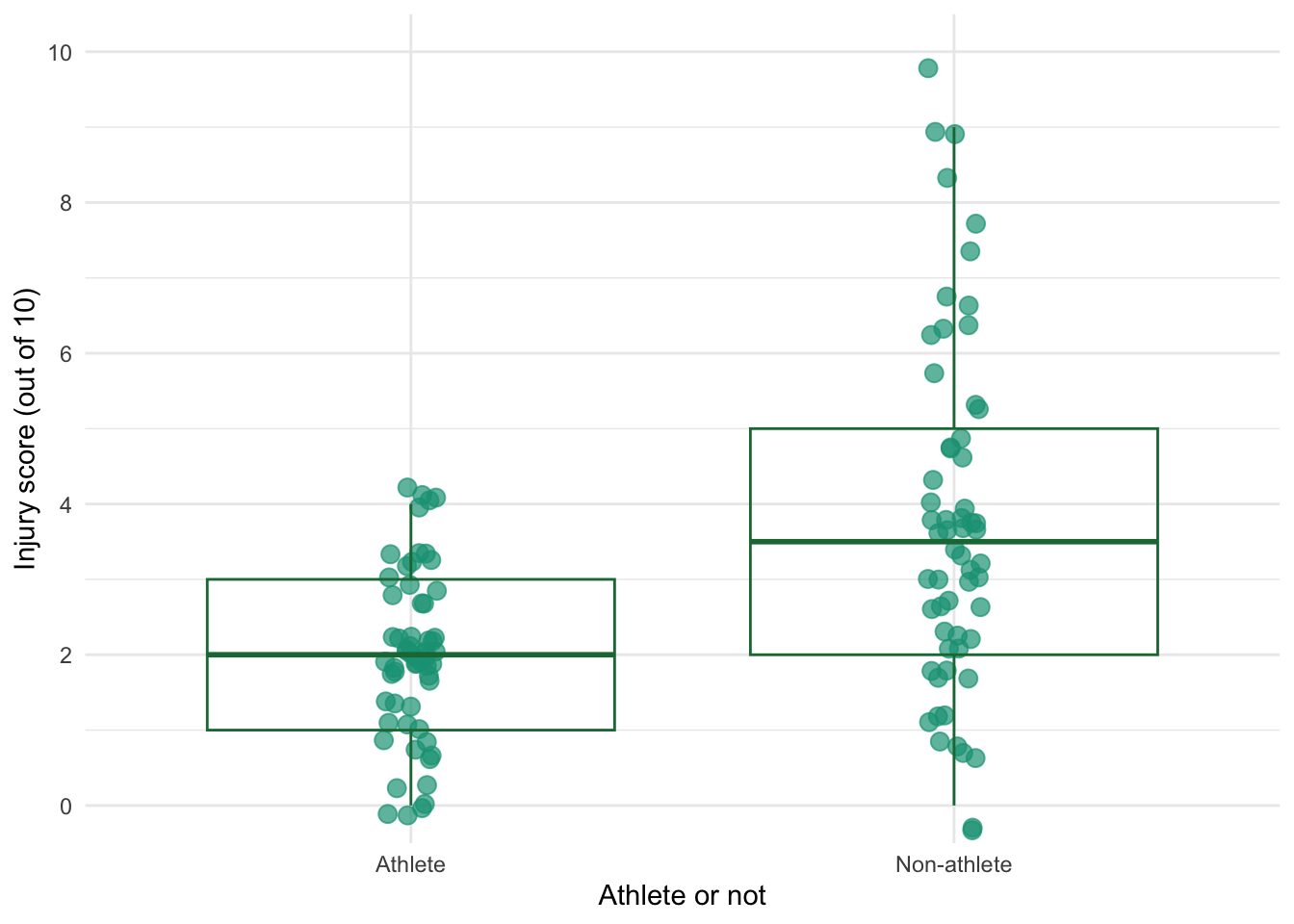
There was a significant main effect of stretching, F(1, 112) = 11.05, p = 0.001, \(\eta_p^2\) = 0.09. Figure 297 shows that stretching significantly decreased injury score compared to not stretching. However, the two-way interaction with athletes will show us that this is true only for athletes and non-athletes who played on the switch, not for those in the control group (you can also see this pattern in the three-way interaction plot). This is an example of how main effects can be misleading.
There was also a significant main effect of switch, F(1, 112) = 55.66, p < .001, \(\eta_p^2\) = 0.33. Figure 298 shows (not surprisingly) that playing on the switch resulted in a significantly higher injury score compared to watching other people playing on the switch (control).
There was not a significant athlete by stretch interaction F(1, 112) = 1.23, p = 0.270, \(\eta_p^2\) = 0.01. Figure 299 shows that (not taking into account playing vs. watching the switch) while non-athletes had higher injury scores than athletes overall, stretching decreased the number of injuries in both athletes and non-athletes by roughly the same amount (compare the vertical distance between the the circle and triangle in each group).
There was a significant athlete by switch interaction F(1, 112) = 45.18, p < .001, \(\eta_p^2\) = 0.29. Figure 300 shows that (not taking stretching into account) non-athletes had low injury scores when watching but high injury scores when playing whereas athletes had low injury scores both when playing and watching.
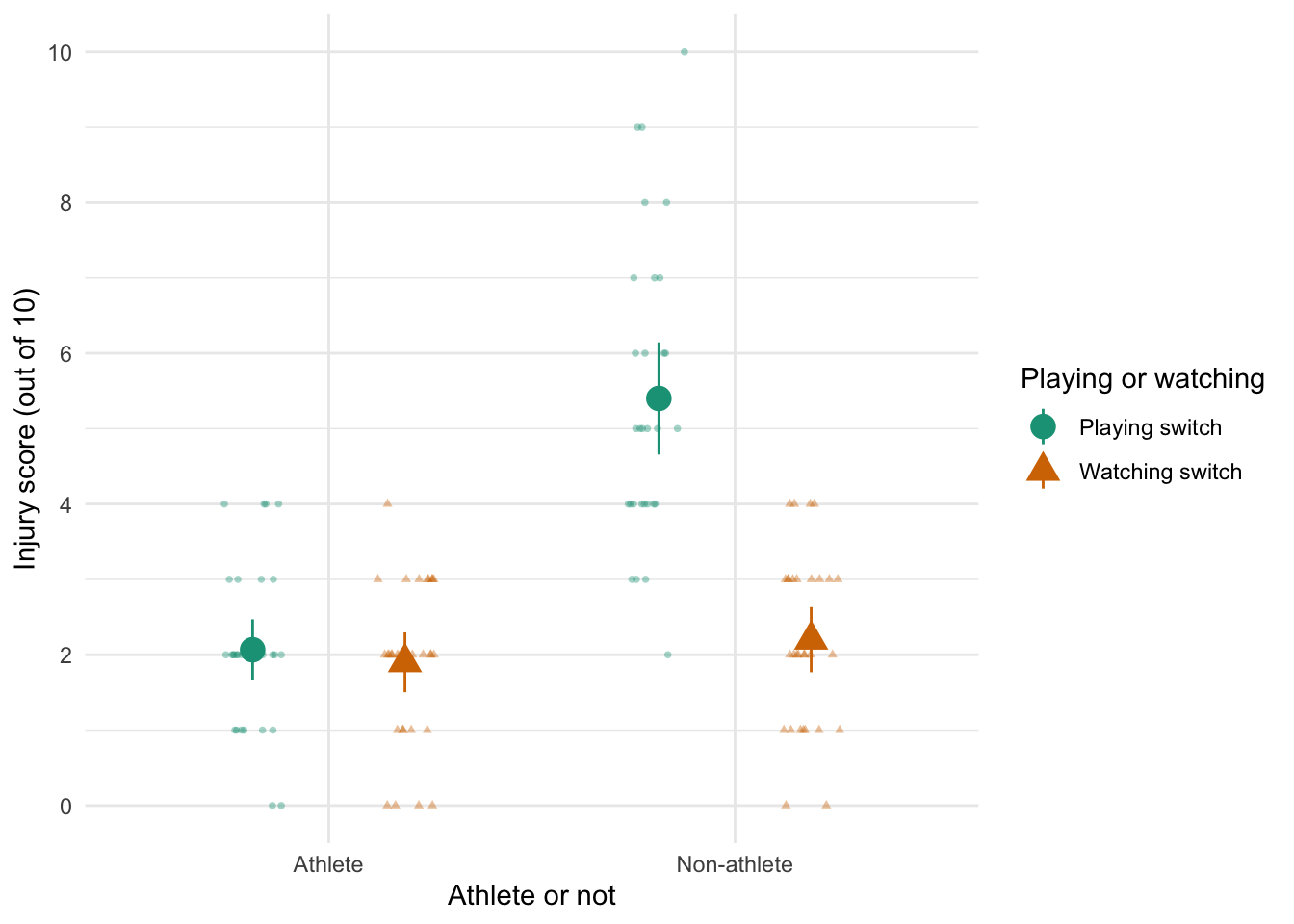
There was a significant stretch by switch interaction F(1, 112) = 14.19, p < .001, \(\eta_p^2\) = 0.11. Figure 301 shows that (not taking athlete into account) stretching before playing on the switch significantly decreased injury scores, but stretching before watching other people playing on the switch did not significantly reduce injury scores. This is not surprising as watching other people playing on the switch is unlikely to result in sports injury!
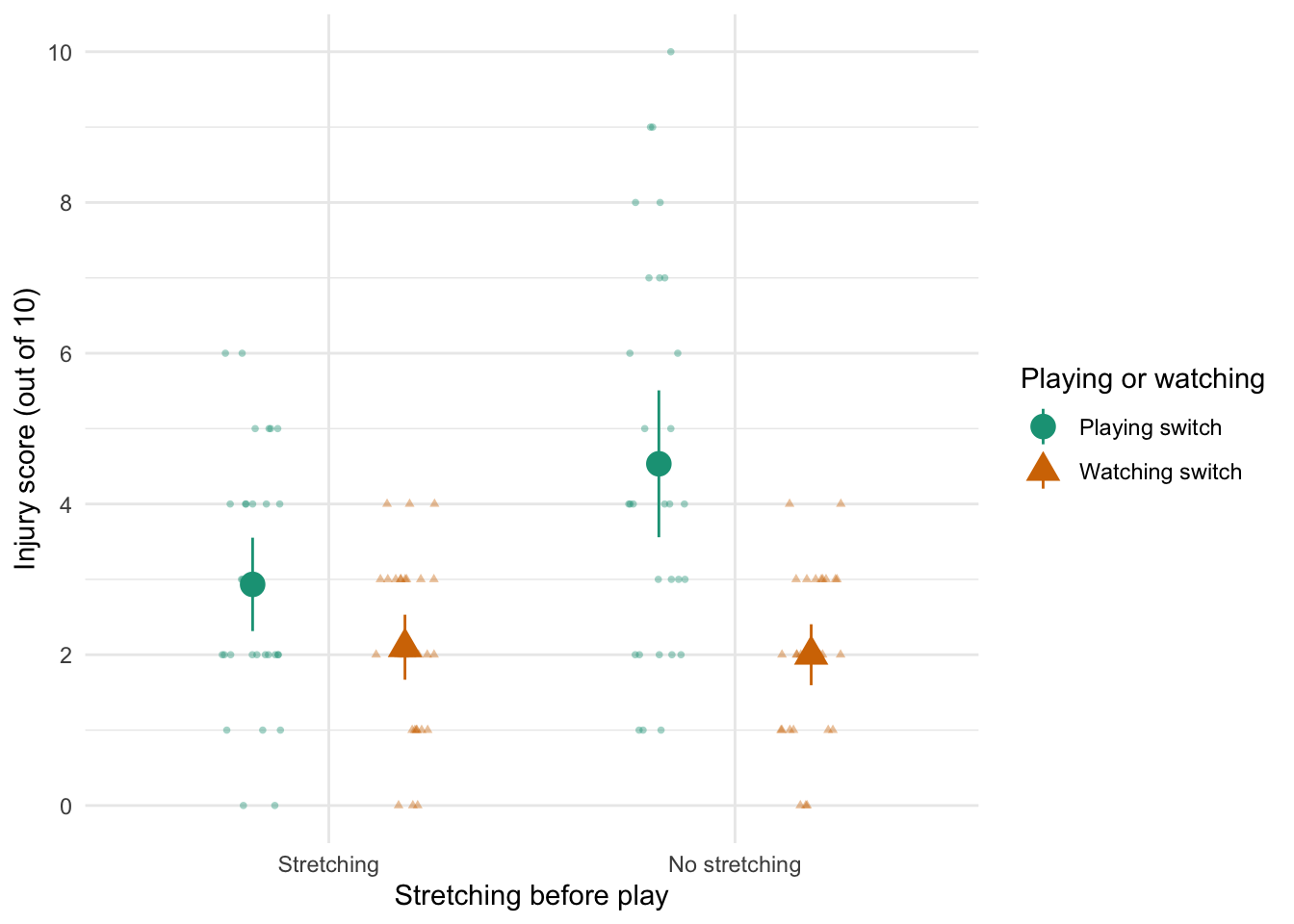
There was a significant athlete by stretch by switch interaction F(1, 112) = 5.94, p < .05, \(\eta_p^2\) = 0.05. What this means is that the effect of stretching and playing on the switch on injury score was different for athletes than it was for non-athletes. In the presence of this significant interaction it makes no sense to interpret the main effects. Figure 302 shows this three-way effect and includes the significance of the simple effects analysis in Figure 295. Using this information, it seems that for athletes, stretching and playing on the switch has very little effect: their injury scores were low regardless of whether they played on the switch, watched other people playing, stretched or did not stretch. However, for the non-athletes, watching other people play on the switch compared to playing it themselves significantly decreased injuries both when they stretched and did not stretch. Based on the means it looks as though this difference is a little smaller after stretching than not (although we don’t have a direct test of this).
Task 14.9
A researcher was interested in what factors contributed to injuries resulting from game console use. She tested 40 participants who were randomly assigned to either an active or static game played on either a Nintendo Switch or Xbox One Kinect. At the end of the session their physical condition was evaluated on an injury severity scale. The data are in the file
xbox.savwhich contains the variablesgame(0 = static, 1 = active),console(0 = Switch, 1 = Xbox), andinjury(a score ranging from 0 (no injury) to 20 (severe injury)). Fit a model to see whether injury severity is significantly predicted from the type of game, the type of console and their interaction.
To fit the model, follow the general procedure. Access the main dialog box and
- Drag the outcome variable (
injury) to the box labelled Dependent Variable. - Drag the predictor variables (
game, andconsole) to the box labelled Fixed Factor(s).
Your completed dialog box should look like Figure 303 Click  and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click
and select the options in Figure 272 to get some post hoc tests and simple effects analyses. Click  and select the options in Figure 235 to get effect sizes and other useful information.
and select the options in Figure 235 to get effect sizes and other useful information.
The main summary table is in Figure 304 and Figure 305 shows simple effects analysis for the two-way interaction. The two-way interaction is significant and so supersedes all lower-order effects. Figure 306 show sthe interaction and the p-values for the simple effects in Figure 305.
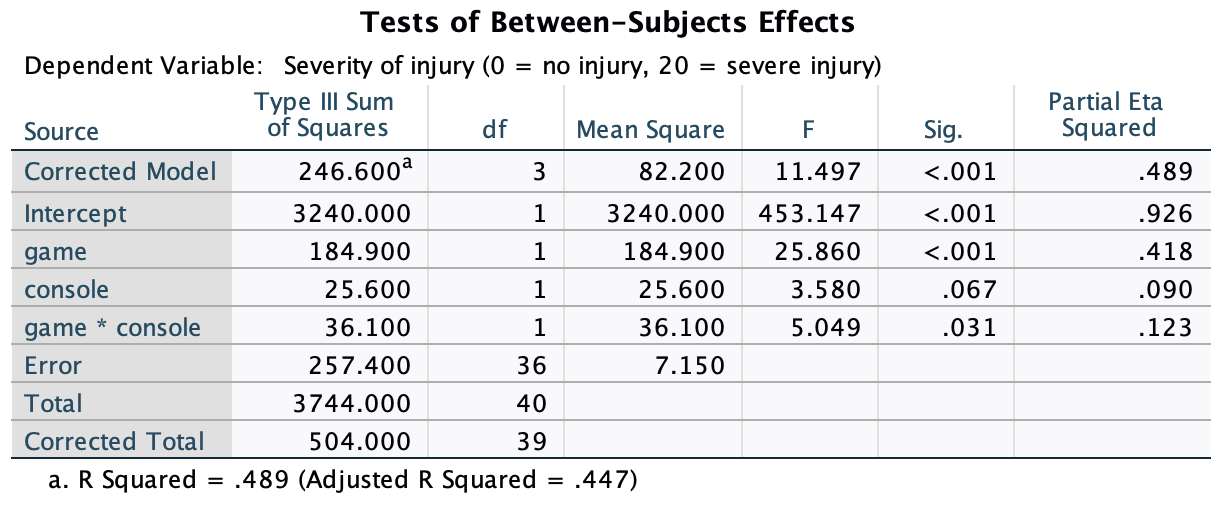
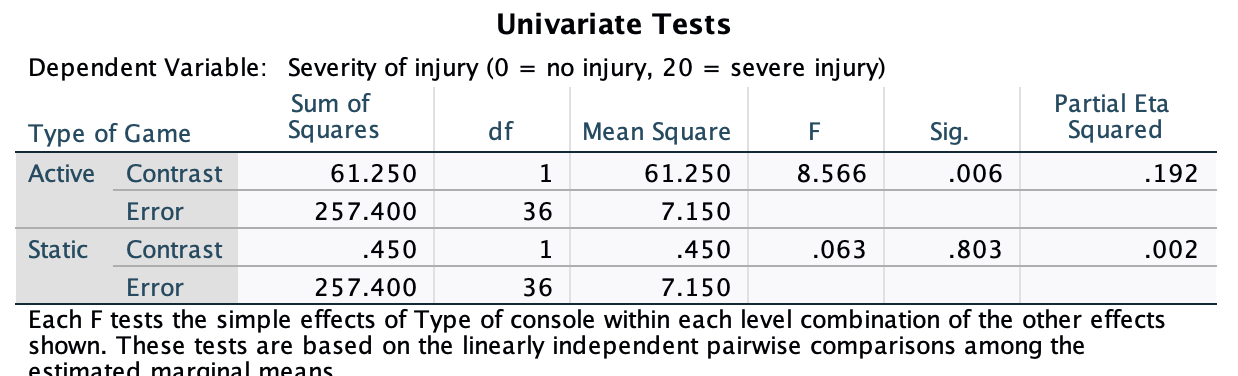
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'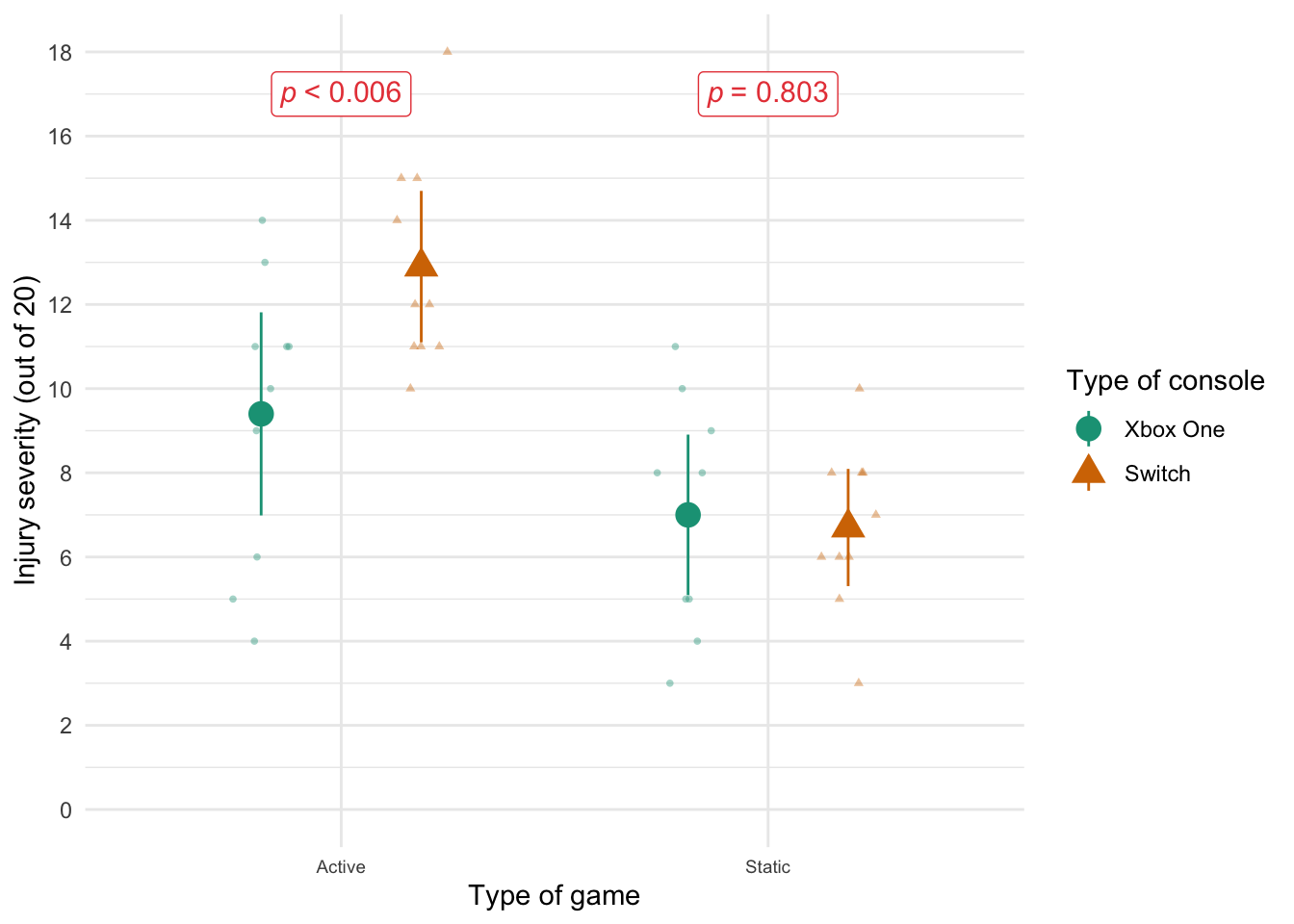
Chapter 15
Task 15.1
It is common that lecturers obtain reputations for being ‘hard’ or ‘light’ markers, but there is often little to substantiate these reputations. A group of students investigated the consistency of marking by submitting the same essays to four different lecturers. The outcome was the percentage mark given by each lecturer and the predictor was the lecturer who marked the report (
tutor_marks.sav). Compute the F-statistic for the effect of marker by hand.
There were eight essays, each marked by four different lecturers. The data are in Table 10 The mean mark that each essay received and the variance of marks for a particular essay are shown too. Now, the total variance within essay marks will in part be due to different lecturers marking (some are more critical and some more lenient), and in part by the fact that the essays themselves differ in quality (individual differences). Our job is to tease apart these sources.
| Essay id | Tutor 1 | Tutor 2 | Tutor 3 | Tutor 4 | \(\overline{X}_\text{essay}\) | \(s_\text{essay}^2\) |
|---|---|---|---|---|---|---|
| qegggt | 62 | 58 | 63 | 64 | 61.75 | 6.92 |
| nghnol | 63 | 60 | 68 | 65 | 64.00 | 11.33 |
| gcomqu | 65 | 61 | 72 | 65 | 65.75 | 20.92 |
| hphjhp | 68 | 64 | 58 | 61 | 62.75 | 18.25 |
| jrcbpi | 69 | 65 | 54 | 59 | 61.75 | 43.58 |
| acnlxu | 71 | 67 | 65 | 50 | 63.25 | 84.25 |
| tenwth | 78 | 66 | 67 | 50 | 65.25 | 132.92 |
| unwyka | 75 | 73 | 75 | 45 | 67.00 | 216.00 |
The total sum of squares
The \(\text{SS}_\text{T}\) is calculated as:
\[ \text{SS}_\text{T} = \sum_{i=1}^{N} (x_i-\overline{X})^2 \]
To use this equation we need the overall mean of all marks (regardless of the essay marked or who marked it). Table 11 shows descriptive statistics for all marks. The grand mean (the mean of all scores) is 63.94.
| Mean | SD | IQR | Min | Max | n |
|---|---|---|---|---|---|
| 63.94 | 7.42 | 7.75 | 45 | 78 | 32 |
To get the total sum of squares, we take each mark, subtract from it the mean of all scores (63.94) and square this difference (that’s the \((x_i-\overline{X})^2\) in the equation) to get the squared errors. Table 12 shows this process. We then add these squared differences to get the sum of squared error:
\[ \begin{aligned} \text{SS}_\text{T} &= 3.76 + 35.28 + 0.88 + 0.00 + 0.88 + 15.52 + 16.48 + 1.12 + \\ &\quad 1.12 + 8.64 + 64.96 + 1.12 + 16.48 + 0.00 + 35.28 + 8.64 +\\ &\quad 25.60 + 1.12 + 98.80 + 24.40 + 49.84 + 9.36 + 1.12 + 194.32 +\\ &\quad 197.68 + 4.24 + 9.36 + 194.32 + 122.32 + 82.08 + 122.32 + 358.72 +\\ &= 1705.76 \end{aligned} \]
The degrees of freedom for this sum of squares is \(N–1\), or 31.
| Essay id | Tutor | Mark | Mean | Error (score - mean) | Error squared | |
|---|---|---|---|---|---|---|
| qegggt | Tutor 1 | 62 | 63.94 | -1.94 | 3.76 | |
| qegggt | Tutor 2 | 58 | 63.94 | -5.94 | 35.28 | |
| qegggt | Tutor 3 | 63 | 63.94 | -0.94 | 0.88 | |
| qegggt | Tutor 4 | 64 | 63.94 | 0.06 | 0.00 | |
| nghnol | Tutor 1 | 63 | 63.94 | -0.94 | 0.88 | |
| nghnol | Tutor 2 | 60 | 63.94 | -3.94 | 15.52 | |
| nghnol | Tutor 3 | 68 | 63.94 | 4.06 | 16.48 | |
| nghnol | Tutor 4 | 65 | 63.94 | 1.06 | 1.12 | |
| gcomqu | Tutor 1 | 65 | 63.94 | 1.06 | 1.12 | |
| gcomqu | Tutor 2 | 61 | 63.94 | -2.94 | 8.64 | |
| gcomqu | Tutor 3 | 72 | 63.94 | 8.06 | 64.96 | |
| gcomqu | Tutor 4 | 65 | 63.94 | 1.06 | 1.12 | |
| hphjhp | Tutor 1 | 68 | 63.94 | 4.06 | 16.48 | |
| hphjhp | Tutor 2 | 64 | 63.94 | 0.06 | 0.00 | |
| hphjhp | Tutor 3 | 58 | 63.94 | -5.94 | 35.28 | |
| hphjhp | Tutor 4 | 61 | 63.94 | -2.94 | 8.64 | |
| jrcbpi | Tutor 1 | 69 | 63.94 | 5.06 | 25.60 | |
| jrcbpi | Tutor 2 | 65 | 63.94 | 1.06 | 1.12 | |
| jrcbpi | Tutor 3 | 54 | 63.94 | -9.94 | 98.80 | |
| jrcbpi | Tutor 4 | 59 | 63.94 | -4.94 | 24.40 | |
| acnlxu | Tutor 1 | 71 | 63.94 | 7.06 | 49.84 | |
| acnlxu | Tutor 2 | 67 | 63.94 | 3.06 | 9.36 | |
| acnlxu | Tutor 3 | 65 | 63.94 | 1.06 | 1.12 | |
| acnlxu | Tutor 4 | 50 | 63.94 | -13.94 | 194.32 | |
| tenwth | Tutor 1 | 78 | 63.94 | 14.06 | 197.68 | |
| tenwth | Tutor 2 | 66 | 63.94 | 2.06 | 4.24 | |
| tenwth | Tutor 3 | 67 | 63.94 | 3.06 | 9.36 | |
| tenwth | Tutor 4 | 50 | 63.94 | -13.94 | 194.32 | |
| unwyka | Tutor 1 | 75 | 63.94 | 11.06 | 122.32 | |
| unwyka | Tutor 2 | 73 | 63.94 | 9.06 | 82.08 | |
| unwyka | Tutor 3 | 75 | 63.94 | 11.06 | 122.32 | |
| unwyka | Tutor 4 | 45 | 63.94 | -18.94 | 358.72 | |
| Total | — | — | — | — | — | 1705.76 |
The within-participant sum of squares
The within-participant sum of squares, \(\text{SS}_\text{W}\), is calculated using the variance in marks for each essay, which are shown in Table 10. The ns are the number of scores on which the variances are based (i.e. in this case the number of marks each essay received, which was 4).
\[ \text{SS}_\text{W} = s_\text{essay 1}^2(n_1-1)+s_\text{essay 2}^2(n_2-1) + s_\text{essay 3}^2(n_3-1) +\ldots+ s_\text{essay 8}^2(n_8-1) \]
Using the values in in Table 10 we get
\[ \begin{aligned} \text{SS}_\text{W} &= s_\text{essay 1}^2(n_1-1)+s_\text{essay 2}^2(n_2-1) + s_\text{essay 3}^2(n_3-1) +\ldots+ s_\text{essay 8}^2(n_8-1) \\ &= 6.92(4-1) + 11.33(4-1) + 20.92(4-1) + 18.25(4-1) + \\ &\quad 43.58(4-1) + 84.25(4-1) + 132.92(4-1) + 216.00(4-1)\\ &= 1602.51. \end{aligned} \]
The degrees of freedom for each essay are \(n–1\) (i.e. the number of marks per essay minus 1). To get the total degrees of freedom we add the df for each essay
\[ \begin{aligned} \text{df}_\text{W} &= df_\text{essay 1}+df_\text{essay 2} + df_\text{essay 3} +\ldots+ df_\text{essay 8} \\ &= (4-1) + (4-1) + (4-1) + (4-1) + (4-1) + (4-1) + (4-1) + (4-1)\\ &= 24 \end{aligned} \]
A shortcut would be to multiply the degrees of freedom per essay (3) by the number of essays (8): \(3 \times 8 = 24\)
The model sum of squares
We calculate the model sum of squares \(\text{SS}_\text{M}\) as:
\[ \sum_{g = 1}^{k}n_g(\overline{x}_g-\overline{x}_\text{grand})^2 \]
Therefore, we need to subtract the mean of all marks (in Table 10) from the mean mark awarded by each tutor (in Table 13), then squares these differences, multiply them by the number of essays marked and sum the results.
| tutor | Mean | Variance |
|---|---|---|
| Tutor 1 | 68.88 | 31.84 |
| Tutor 2 | 64.25 | 22.21 |
| Tutor 3 | 65.25 | 47.93 |
| Tutor 4 | 57.38 | 62.55 |
Using the values in Table 13, \(\text{SS}_\text{M}\) is
\[ \begin{aligned} \text{SS}_\text{M} &= 8(68.88 – 63.94)^2 +8(64.25 – 63.94)^2 + 8(65.25 – 63.94)^2 + 8(57.38–63.94)^2\\ &= 554 \end{aligned} \] The degrees of freedom are the number of conditions (in this case the number of markers) minus 1, \(df_M = k-1 = 3\)
The residual sum of squares
We now know that there are 1706 units of variation to be explained in our data, and that the variation across our conditions accounts for 1602 units. Of these 1602 units, our experimental manipulation can explain 554 units. The final sum of squares is the residual sum of squares (\(\text{SS}_\text{R}\)), which tells us how much of the variation cannot be explained by the model. Knowing \(\text{SS}_\text{W}\) and \(\text{SS}_\text{M}\) already, the simplest way to calculate \(\text{SS}_\text{R}\) is through subtraction
\[ \begin{aligned} \text{SS}_\text{R} &= \text{SS}_\text{W}-\text{SS}_\text{M}\\ &=1602.51-554\\ &=1048.51. \end{aligned} \]
The degrees of freedom are calculated in a similar way
\[ \begin{aligned} df_\text{R} &= df_\text{W}-df_\text{M}\\ &= 24-3\\ &= 21. \end{aligned} \]
The mean squares
Next, convert the sums of squares to mean squares by dividing by their degrees of freedom
\[ \begin{aligned} \text{MS}_\text{M} &= \frac{\text{SS}_\text{M}}{df_\text{M}} = \frac{554}{3} = 184.67 \\ \text{MS}_\text{R} &= \frac{\text{SS}_\text{R}}{df_\text{R}} = \frac{1048.51}{21} = 49.93. \\ \end{aligned} \]
The F-statistic
The F-statistic is calculated by dividing the model mean squares by the residual mean squares:
\[ F = \frac{\text{MS}_\text{M}}{\text{MS}_\text{R}} = \frac{184.67}{49.93} = 3.70. \]
This value of F can be compared against a critical value based on its degrees of freedom (which are 3 and 21 in this case).
Task 15.2
Repeat the analysis for Task 1 using SPSS Statistics and interpret the results.
To fit the model, follow the general procedure.
- Type a name (I typed
marker) for the repeated measures variable in the box labelled Within-Subject Factor Name: - Enter the number of levels of the repeated measures variable (4) in the box labelled Number of Levels:
- Click
 to register the variable
to register the variable - Click
 to define the variable
to define the variable - Move the variables representing the levels of your repeated measures variable) to the box labelled Within-Subjects Variables
This process is shown in Figure 308. Select the options in the general procedure and to get some Bonferroni post hoc tests set the options in Figure 309.
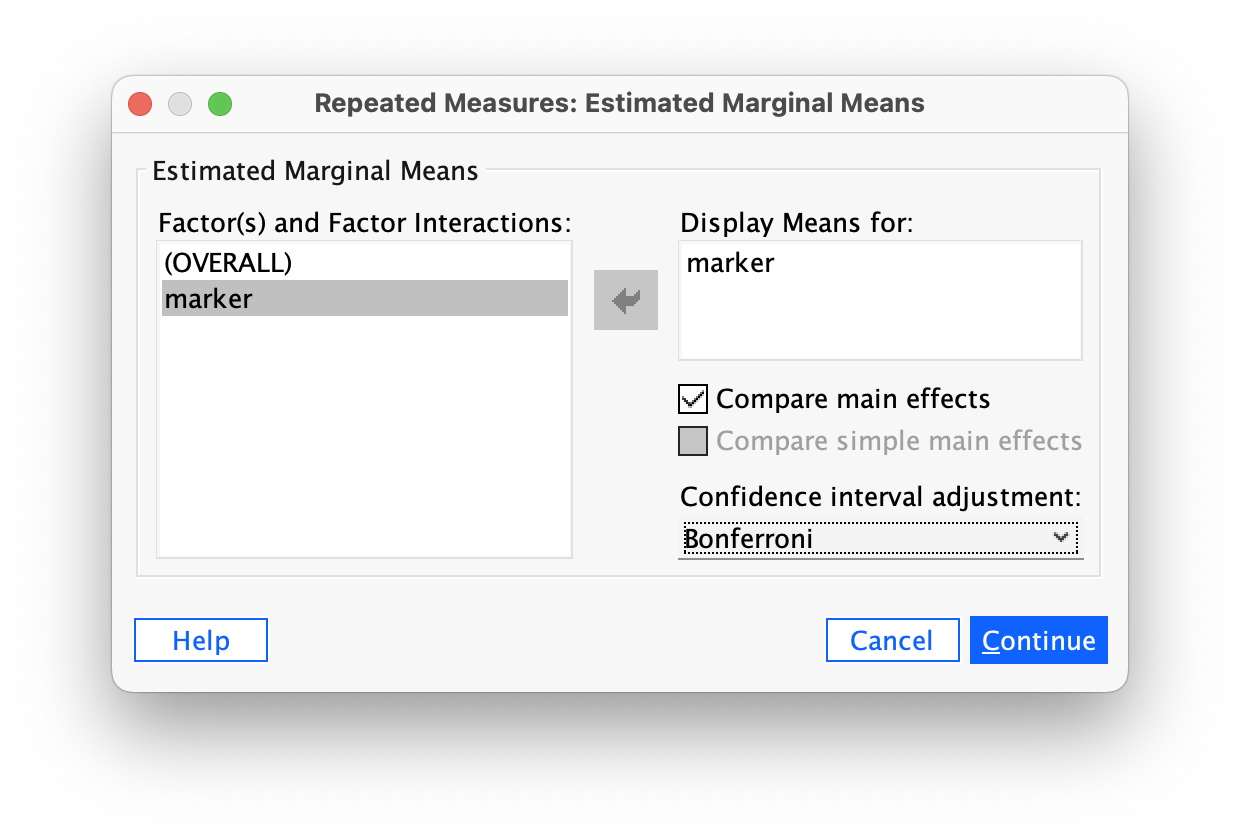
You’ll find in your output that Mauchley’s test indicates a significant violation of sphericity, but I have argued in the book that you should ignore this test and routinely correct for sphericity, so that’s what we’ll do. Figure 310 tells us about the main effect of marker. If we look at the Greenhouse-Geisser corrected values, we would conclude that tutors did not significantly differ in the marks they award, F(1.67, 89.53) = 3.70, p = 0.063. If, however, we look at the Huynh-Feldt corrected values, we would conclude that tutors did significantly differ in the marks they award, F(2.14, 70.09) = 3.70, p = 0.047. Which to believe then? Well, this example illustrates just how silly it is to have a categorical threshold like p < 0.05 that lead to completely opposite conclusions. The best course of action here would be report both results openly, compute some effect sizes and focus more on the size of the effect than its p-value.
Figure 311 shows the Bonferroni post hoc tests, which we should ignore if we’re wedded to p-values. The only significant difference between group means is between Prof Field (marker 1) and Prof Smith (marker 2). Looking at the means of these markers, we can see that I give significantly higher marks than Prof Smith. However, there is a rather anomalous result in that there is no significant difference between the marks given by Prof Death (marker 4) and myself, even though the mean difference between our marks is higher (11.5) than the mean difference between myself and Prof Smith (4.6). The reason is the sphericity in the data. The interested reader might like to run some correlations between the four tutors’ grades. You will find that there is a very high positive correlation between the marks given by Prof Smith and myself (indicating a low level of variability in our data). However, there is a very low correlation between the marks given by Prof Death and myself (indicating a high level of variability between our marks). It is this large variability between Prof Death and myself that has produced the non-significant result despite the average marks being very different (this observation is also evident from the standard errors).
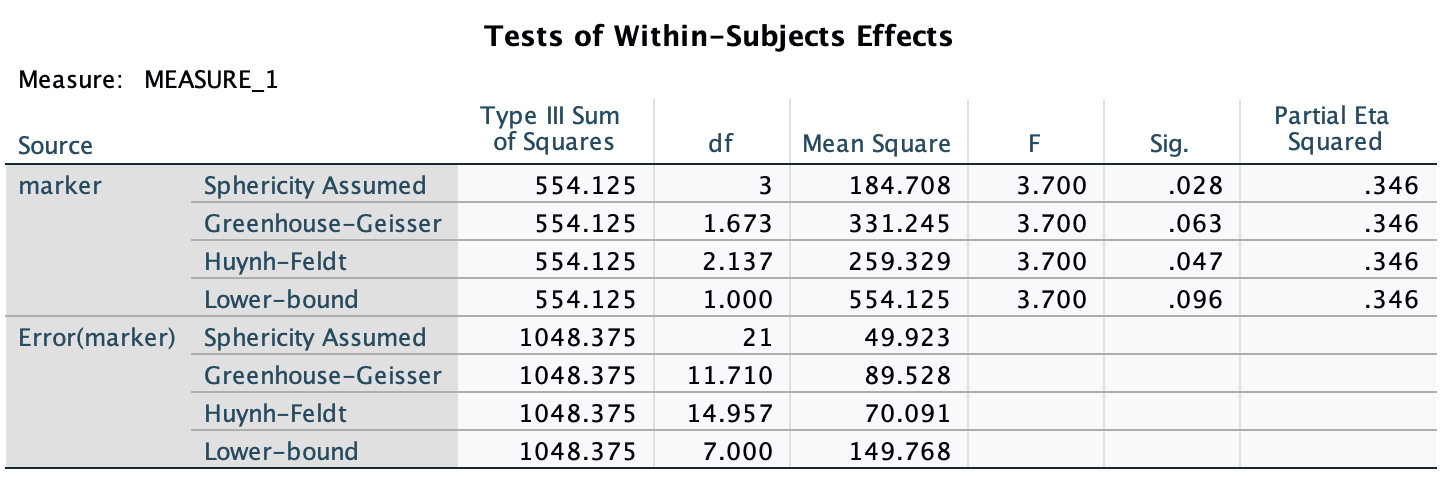
Task 15.3
Calculate the effect sizes for the analysis in Task 1.
In repeated-measures ANOVA, the equation for \(\omega^2\) is:
\[ \omega^2 = \frac{[\frac{k-1}{nk}(\text{MS}_\text{M}-\text{MS}_\text{R})]}{\text{MS}_\text{R}+\frac{\text{MS}_\text{B}-\text{MS}_\text{R}}{k}+[\frac{k-1}{nk}(\text{MS}_\text{M}-\text{MS}_\text{R})]} \]
To get \(\text{MS}_\text{B}\) we need \(\text{SS}_\text{W}\), which is not in the output. However, we can obtain it as follows:
\[ \begin{aligned} \text{SS}_\text{T} &= \text{SS}_\text{B} + \text{SS}_\text{M} + \text{SS}_\text{R} \\ \text{SS}_\text{B} &= \text{SS}_\text{T} - \text{SS}_\text{M} - \text{SS}_\text{R} \\ \end{aligned} \]
The next problem is that the output also doesn’t include \(\text{SS}_\text{T}\) but we have the value from Task 1. You should get:
\[ \begin{aligned} \text{SS}_\text{B} &= 1705.868-554.125-1048.375 \\ &=103.37 \end{aligned} \]
The next step is to convert this to a mean squares by dividing by the degrees of freedom, which in this case are the number of essays minus 1:
\[ \begin{aligned} \text{MS}_\text{B} &= \frac{\text{SS}_\text{B}}{df_\text{B}} = \frac{\text{SS}_\text{B}}{N-1} \\ &=\frac{103.37}{8-1} \\ &= 14.77 \end{aligned} \]
The resulting effect size is:
\[ \begin{aligned} \omega^2 &= \frac{[\frac{4-1}{8 \times 4}(184.71-49.92)]}{49.92+\frac{14.77-49.92}{4}+[\frac{4-1}{8 \times4}(184.71-49.92)]} \\ &= \frac{12.64}{53.77} \\ &\simeq 0.24. \end{aligned} \]
Task 15.4
In the previous chapter we came across the beer-goggles effect. In that chapter, we saw that the beer-goggles effect was stronger for unattractive faces. We took a follow-up sample of 26 people and gave them doses of alcohol (0 pints, 2 pints, 4 pints and 6 pints of lager) over four different weeks. We asked them to rate a bunch of photos of unattractive faces in either dim or bright lighting. The outcome measure was the mean attractiveness rating (out of 100) of the faces and the predictors were the dose of alcohol and the lighting conditions (
goggles_lighting.sav). Do alcohol dose and lighting interact to magnify the beer goggles effect?
To fit the model, follow the general procedure.
- In the first dialog box type a name (I typed
lighting) for the first repeated measures variable in the box labelled Within-Subject Factor Name: - Enter the number of levels of the repeated measures variable (2) in the box labelled Number of Levels:
- Click
 to register the variable
to register the variable - Type a name (I typed
alcohol) for the second repeated measures variable in the box labelled Within-Subject Factor Name: - Enter the number of levels of the repeated measures variable (4) in the box labelled Number of Levels:
- Click
 to register the variable
to register the variable - Click
 to define the variables
to define the variables - Move the variables representing the levels of your repeated measures variable) to the box labelled Within-Subjects Variables in the appropriate order
This process is shown in Figure 312. Set the options in the general procedure, and to get simple effects for the interaction (which you’ll need in the next task) click  and select the options in Figure 313.
and select the options in Figure 313.
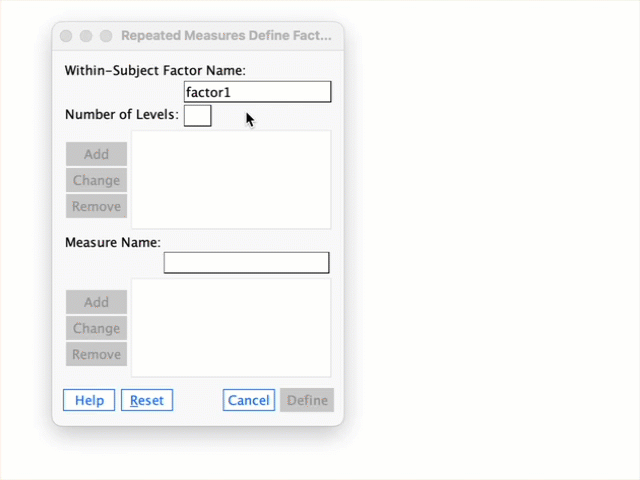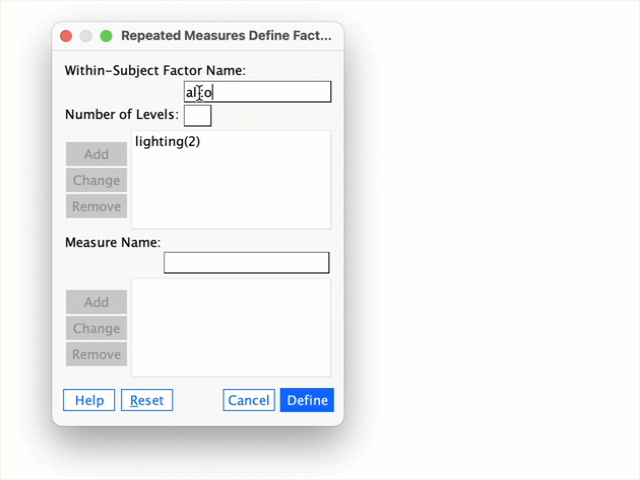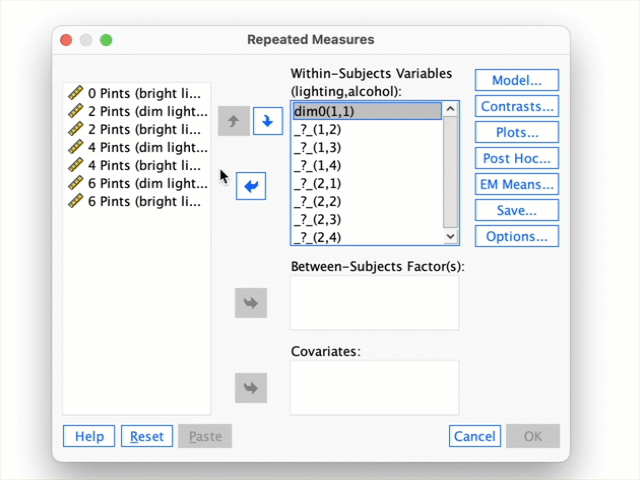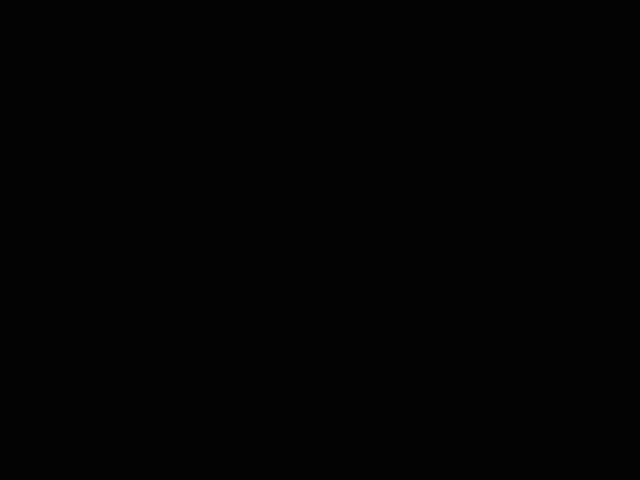
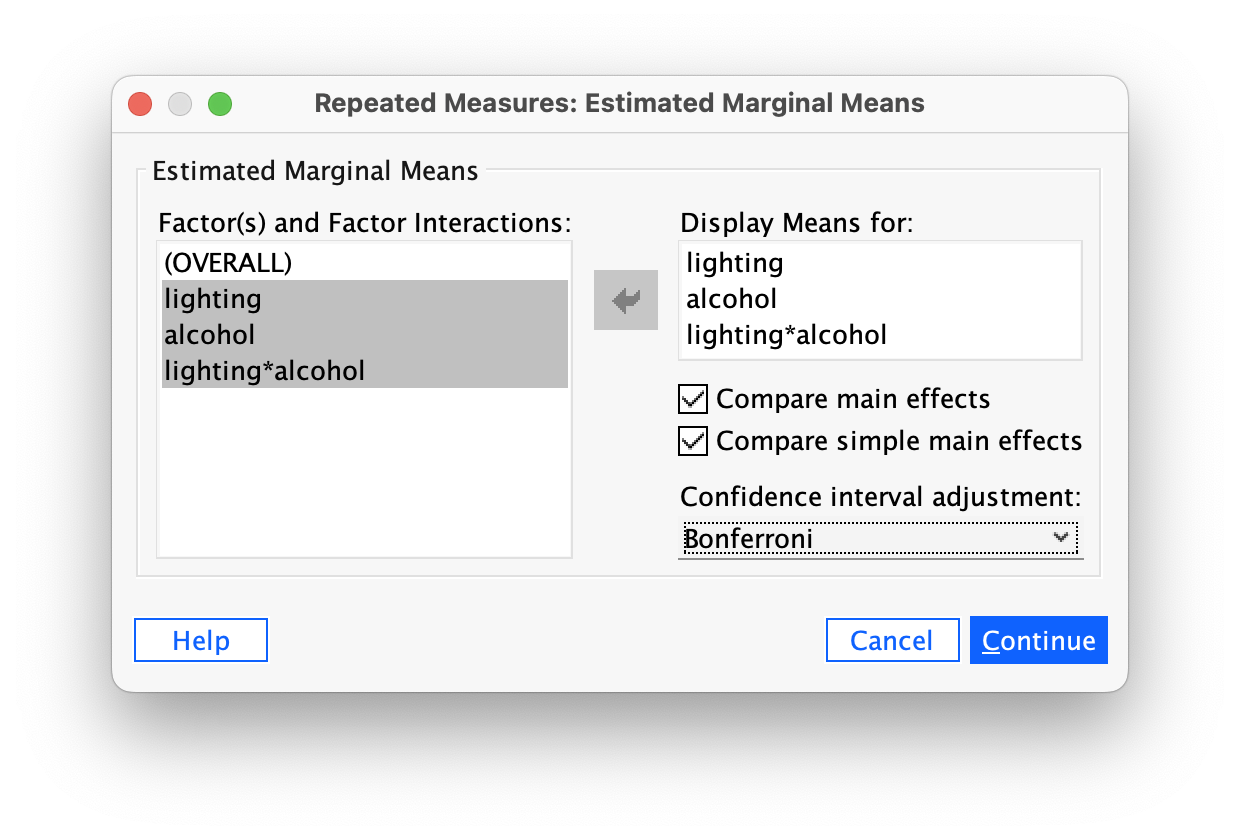
In your output Mauchley’s test will indicates a non-significant violation of sphericity for both variables, but I have argued that you should ignore this test and routinely apply the Greenhouse-Geisser correction, so that’s what we’ll do. Figure 314 shows the main output, note I have used the tip in the book to show only the Greenhouse-Geisser corrected results. All effects are significant at p < 0.001. We’ll look at each effect in turn.
The main effect of lighting shows that the attractiveness ratings of photos was significantly lower when the lighting was dim compared to when it was bright, F(1, 25) = 23.42, p < 0.001, \(\eta_p^2\) = 0.48. The main effect of alcohol shows that the attractiveness ratings of photos of faces was significantly affected by how much alcohol was consumed, F(2.62, 65.47) = 104.39, p < 0.001, \(\eta_p^2\) = 0.81. However, both of these effects are superseded by the interaction, which shows that the effect that alcohol had on ratings of attractiveness was significantly moderated by the brightness of the lighting, F(2.81, 70.23) = 22.22, p < 0.001, \(\eta_p^2\) = 0.47. To interpret this effect let’s move onto the next task.
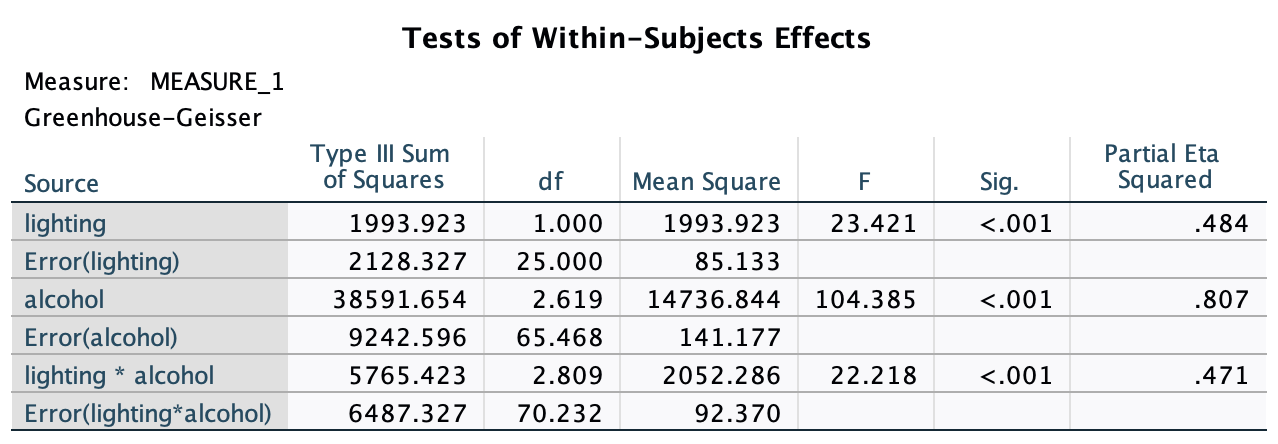
Task 15.5
Interpret the simple effect of effect of alcohol at different levels of lighting.
The interaction effect is shown in Figure 317. Figure 315 shows the simple effect of alcohol at different levels of lighting. These analyses are not particularly helpful because they show that alcohol significantly affected attractiveness ratings both when lights were dim, \(\Lambda\) = 0.05, F(3, 23) = 156.29, p < 0.001, \(\eta_p^2\) = 0.95, and when they were bright, \(\Lambda\) = 0.18, F(3, 23) = 35.99, p < 0.001, \(\eta_p^2\) = 0.82. This is an example where it might be worth looking at the alternative simple effects, that is, the simple effect of lighting within each dose of alcohol. These effects are shown in Figure 316 and they are somewhat more useful because they show that lighting did not have a significant effect on attractiveness ratings after no alcohol, \(\Lambda\) = 0.94, F(1, 25) = 1.49, p = 0.23, \(\eta_p^2\) = 0.06, had a slightly significant effect after 2 pints of lager, \(\Lambda\) = 0.85, F(1, 25) = 4.56, p = 0.043, \(\eta_p^2\) = 0.15, and more substantial effects after 4, \(\Lambda\) = 0.48, F(1, 25) = 27.17, p < 0.001, \(\eta_p^2\) = 0.52, and 6 pints, \(\Lambda\) = 0.31, F(1, 25) = 55.59, p < 0.001, \(\eta_p^2\) = 0.69. Basically the effect of lighting is getting stronger as the alcohol dose increases: you can see this on Figure 317 by the circle and triangle getting further apart.
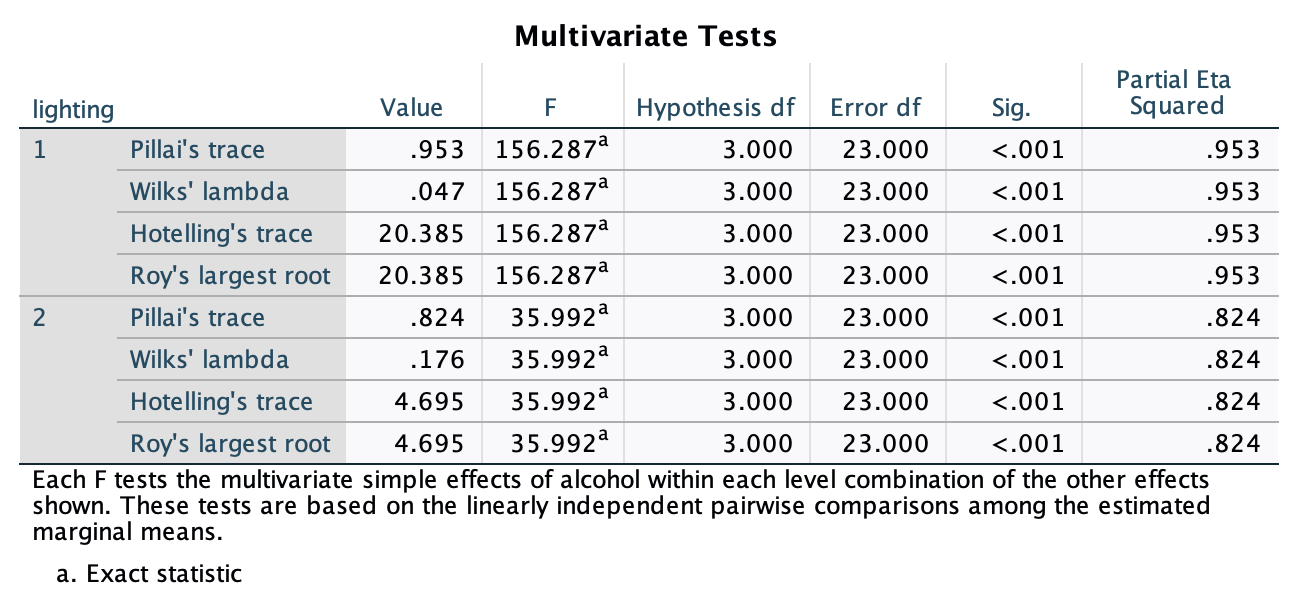
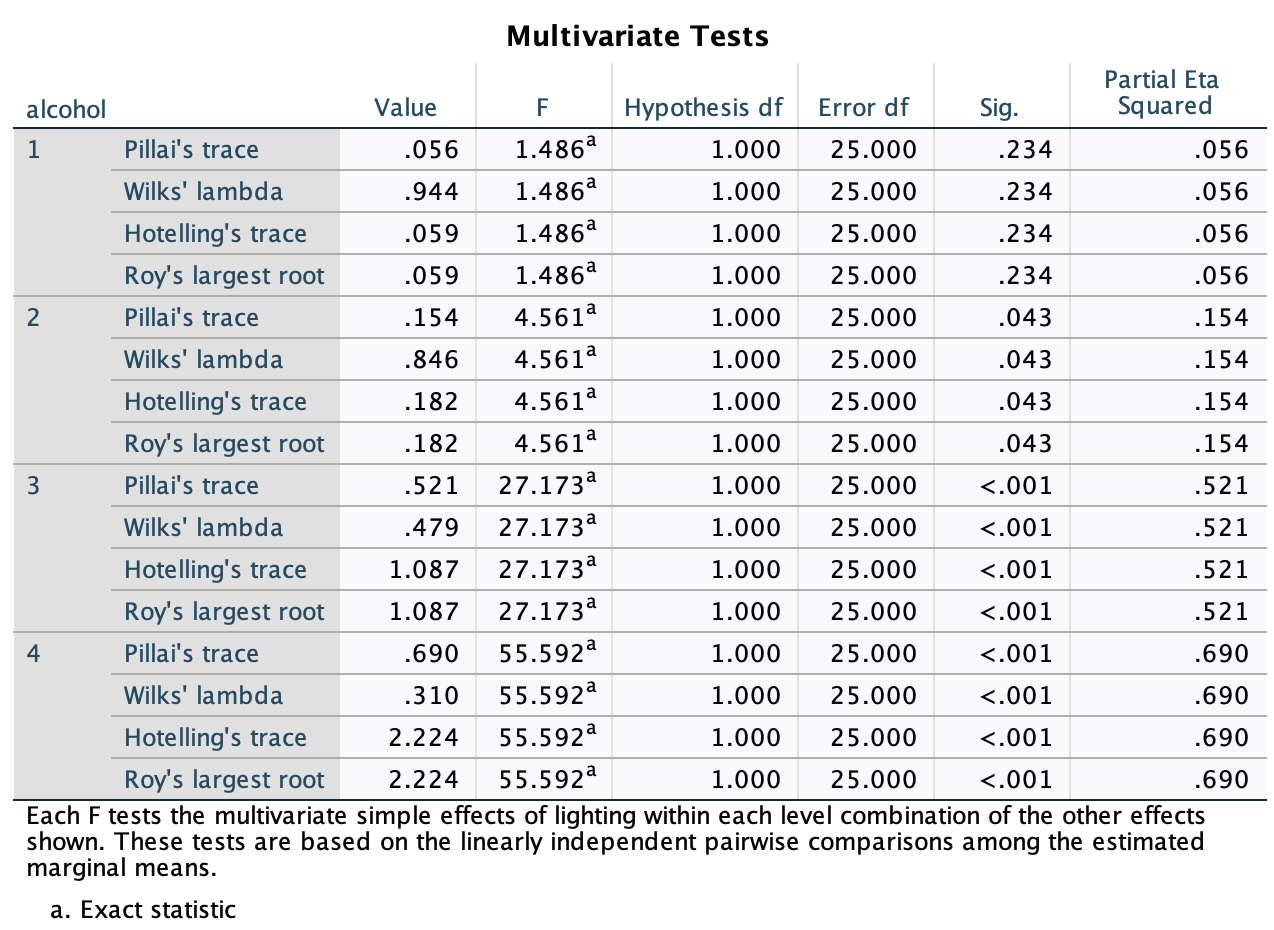
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'
Warning in is.na(x): is.na() applied to non-(list or vector) of type
'expression'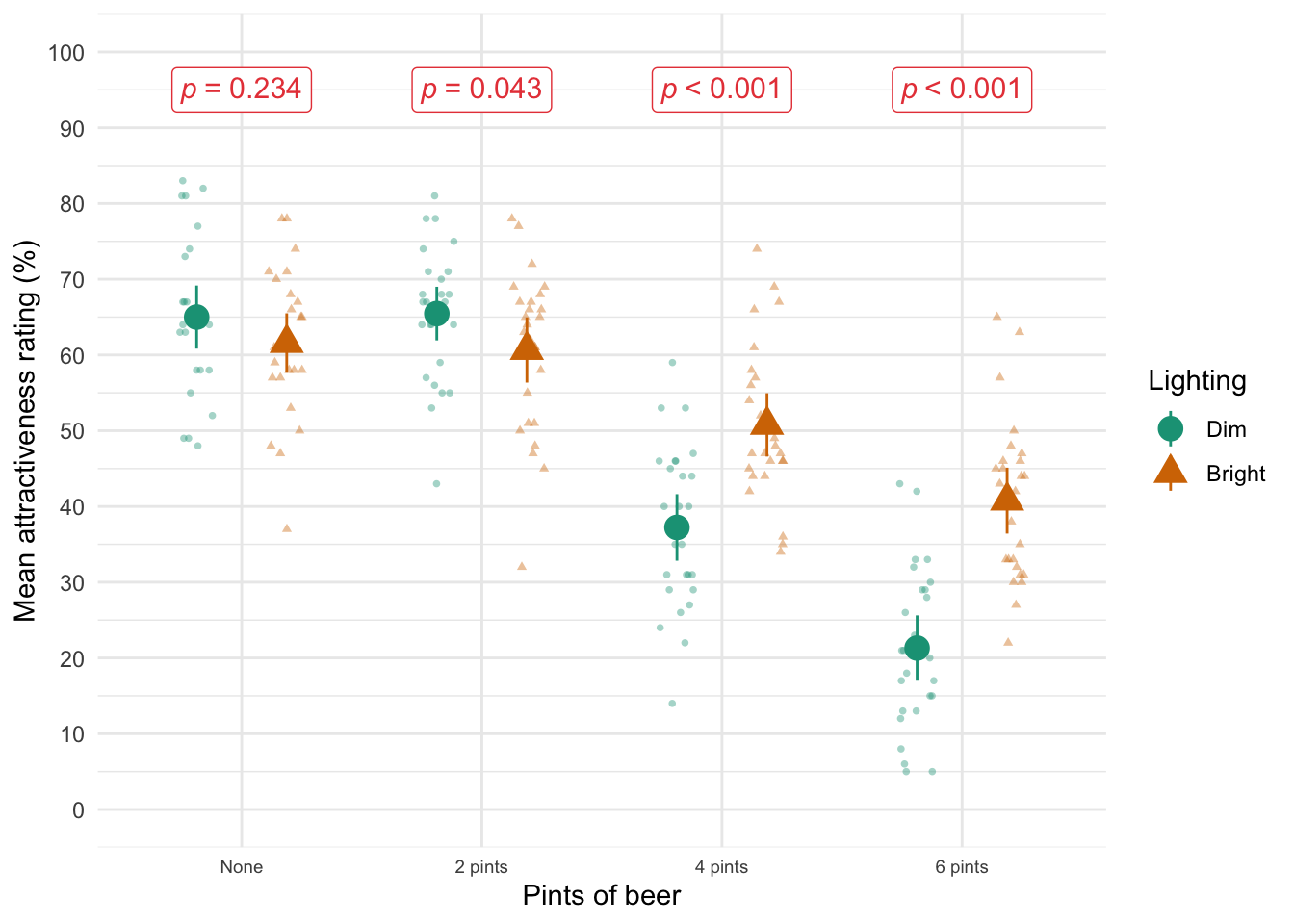
Task 15.6
Early in my career I looked at the effect of giving children information about entities. In one study (Field, 2006), I used three novel entities (the quoll, quokka and cuscus) and children were told negative things about one of the entities, positive things about another, and given no information about the third (our control). After the information I asked the children to place their hands in three wooden boxes each of which they believed contained one of the aforementioned entities (
field_2006.sav). Draw an error bar graph of the means interpret a Q-Q plot.
To produce the error bar chart, access the chart builder and select a bar chart from the gallery. Then
- Select the three variables representing the levels of the repeated measures variable (
bhvneg,bhvpos, andbhvnone) and drag them (simultaneously) to .
. - Your completed dialog box should look like Figure 318. In the Element Properties dialog box remember to select
 to add error bars.
to add error bars.
The resulting plot will look like Figure 319. It looks like children took longer on average to approach the box ‘containing’ an animal that they they had heard threat information about.
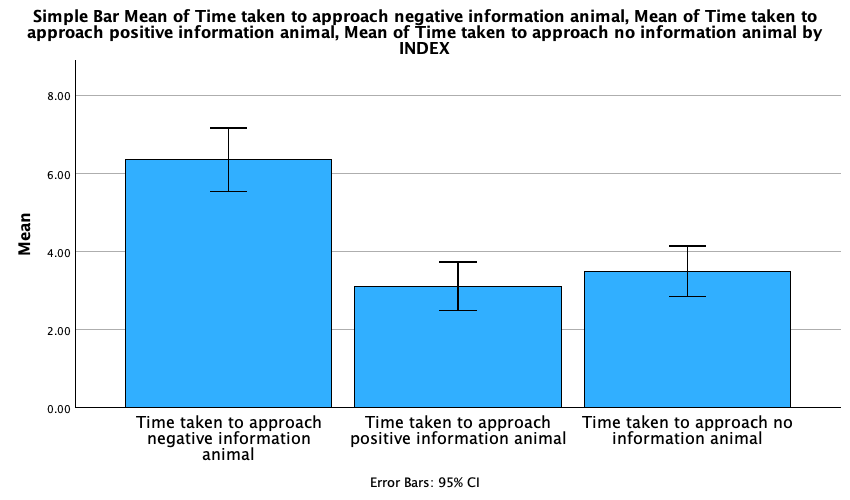
To get the Q-Q plots we can use the Explore command. Follow the general procedure but place all four variables (bhvpos, bhvneg and bhvnone) in the Dependent List section of the main dialog box. The dialog box will look like Figure 320. The resulting plots are shown in Figure 321 to Figure 323. All three variables show are very non-normal. This will be, in part, because if a child hadn’t approached the box within 15 seconds we (for ethical reasons) assumed that they did not want to complete the task and so we assigned a score of 15 and asked them to approach the next box.
These days, given these data, I’d use a robust test (Task 8!) back when I conducted these research these tests were not so readily available and I log-transformed the scores to reduce the skew (a practice I’m not keen on these days). This brings us onto Task 7!
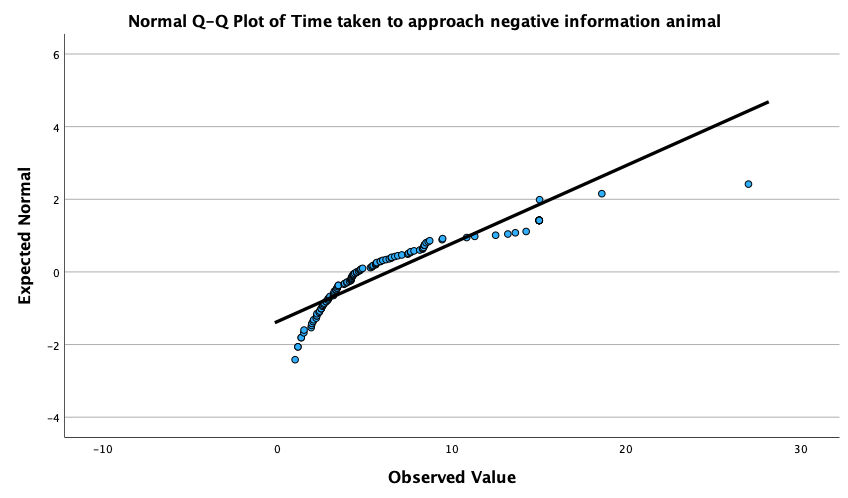
Task 15.7
Log-transform the scores in Task 7, make a Q-Q plot of the transformed scores and interpret it.
The easiest way to conduct these transformations is by executing the following syntax:
COMPUTE ln_negative = ln(bhvneg).
COMPUTE ln_positive = ln(bhvpos).
COMPUTE ln_no_info = ln(bhvnone).
EXECUTE.To get the Q-Q plots repeat the process described in the previous task, but use the new variables you have created. The resulting plots are shown in Figure 324 to Figure 326. All three variables show are a lot more normal than they were (although positive and no information scores still show a lack of normality).
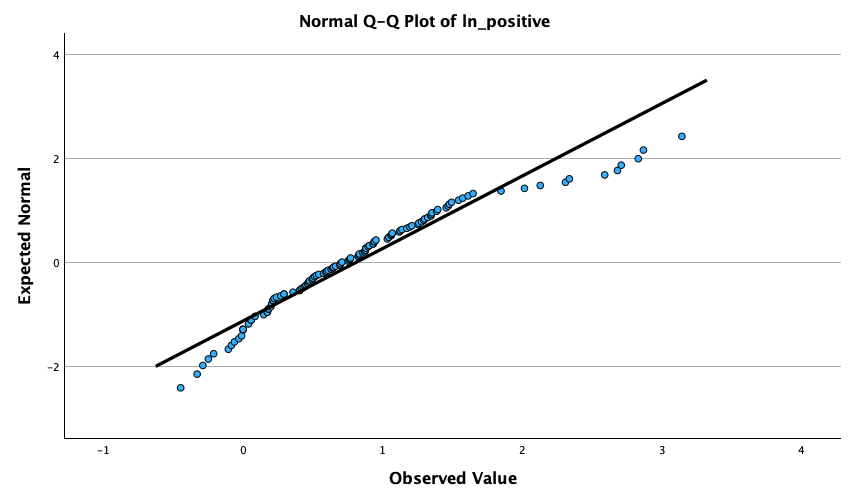
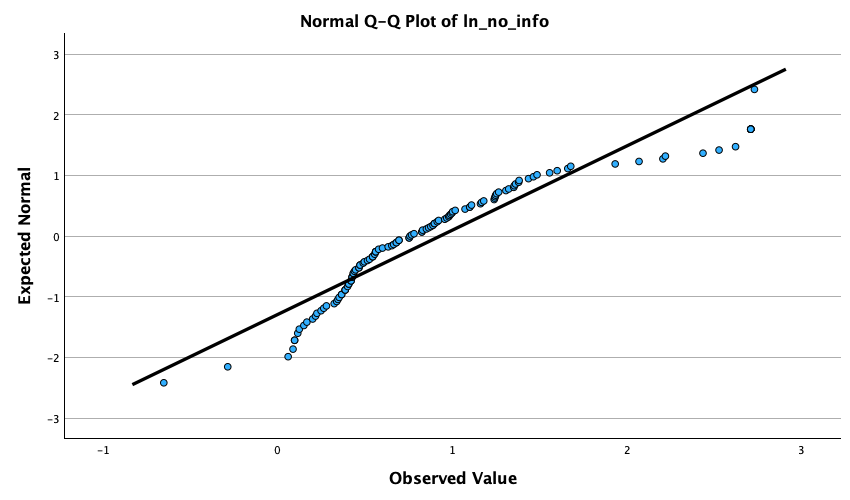
Task 15.8
Analyse the data in Task 7 with a robust model. Do children take longer to put their hands in a box that they believe contains an entity about which they have been told nasty things?
You would adapt the syntax file as follows:
BEGIN PROGRAM R.
library(WRS2)
library(tidyr)
mySPSSdata = spssdata.GetDataFromSPSS(factorMode = "labels")
id <- "code"
rm_factor <- c("bhvneg", "bhvpos", "bhvnone")
df <- pivot_longer(mySPSSdata, cols =all_of(rm_factor), names_to = "variable", values_to = "value")
names(df)[names(df) == id] <- "id"
rmanova(df$value, df$variable, df$id, tr = 0.2)
rmmcp(df$value, df$variable, df$id, tr = 0.2)
END PROGRAM.The results are
Call:
rmanova(y = df$value, groups = df$variable, blocks = df$id, tr = 0.2)
Test statistic: F = 78.1521
Degrees of freedom 1: 1.24
Degrees of freedom 2: 94.32
p-value: 0
Call:
rmmcp(y = df$value, groups = df$variable, blocks = df$id, tr = 0.2)
psihat ci.lower ci.upper p.value p.crit sig
bhvneg vs. bhvpos 2.41558 1.71695 3.11421 0.00000 0.0169 TRUE
bhvneg vs. bhvnone 2.07013 1.35313 2.78713 0.00000 0.0250 TRUE
bhvpos vs. bhvnone -0.20597 -0.40537 -0.00658 0.01351 0.0500 TRUEThe results from the robust model mirror the analysis that I conducted on the log-transformed values in the paper itself (in case you want to check). The main effect of the type of information was significant F(1.24, 94.32) = 78.15, p < 0.001. The post hoc tests show a significantly longer time to approach the box containing the negative information animal compared to the positive information animal, \(\hat{\psi} = 2.42, p_{\text{observed}} < 0.001, p_{\text{crit}} =0.017\), and compared to the no information box, \(\hat{\psi} = 2.07, p_{\text{observed}} < 0.001, p_{\text{crit}} =0.025\). Children also approached the box containing the positive information animal significantly faster than the no information animal, \(\hat{\psi} = -0.21, p_{\text{observed}} = 0.014, p_{\text{crit}} = 0.050\).
Chapter 16
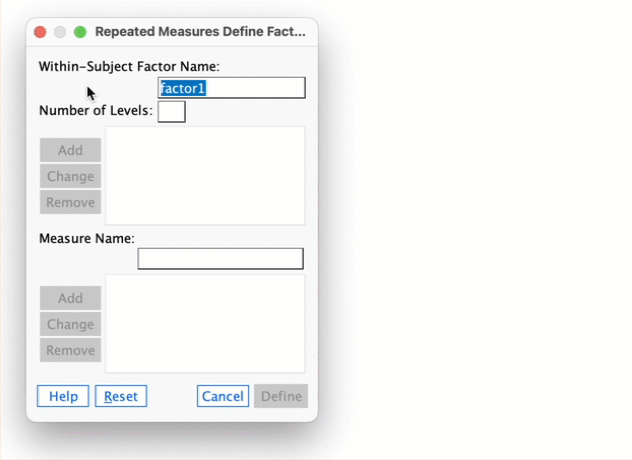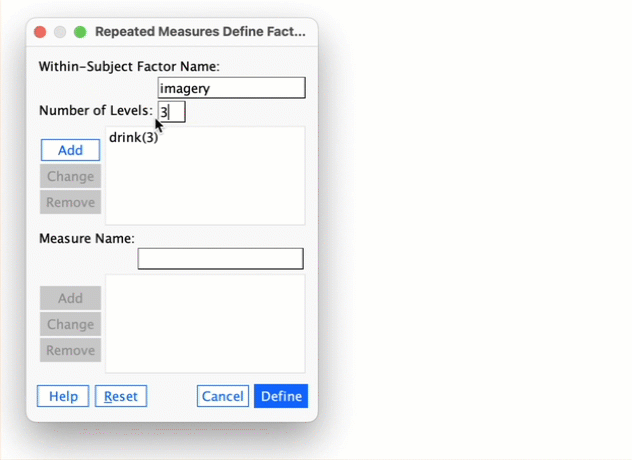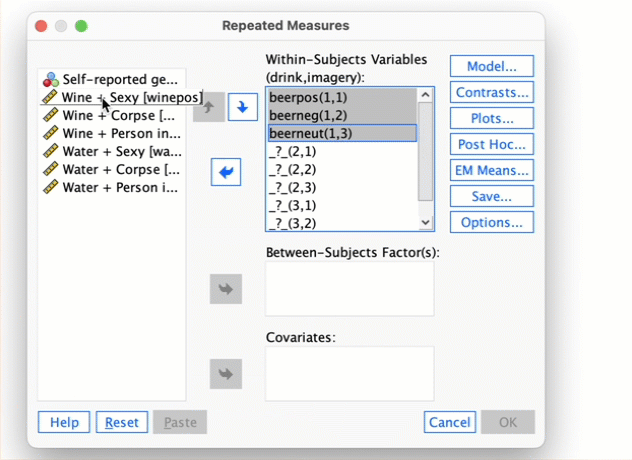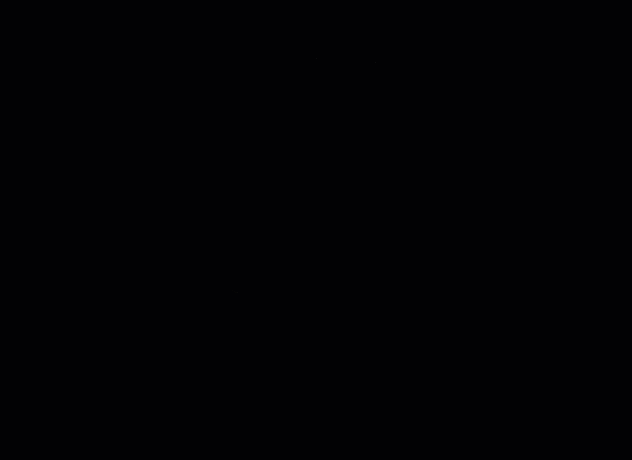
Task 16.1
A marketing researcher was interested in the effects of types of imagery (positive, negative or neutral) on perceptions of different types of drink (beer, wine, water). Participants viewed videos of different drink products in the context of positive, negative or neutral imagery and then rated the products on a scale from –100 (extremely dislike) through 0 (neutral) to 100 (extremely like). Those who identify as men and women might respond differently to the products, so participants self-reported their gender (a between-group variable). The data are in the file
mixed_attitude.sav. Analyse the data to see whether there is a combined effect ofimagery,drinkandgenderon ratings of the products.
To fit the model, follow the general procedure. In this case though we will use contrasts rather than simple effects to break down the three-way interaction. For the drink variable the water condition acts as an obvious control condition (because the other drinks are alcoholic), and for the imagery variable the neutral condition acts as an obvious control condition (because the other images have emotional valence). For this reason, notice that in the the general procedure I have specified the levels of both drink and imagery such that these control categories are last. Therefore, we could set simple contrasts that compare each category to the last, and these will give us the following comparisons
-
drink: we will compare beer against water and wine against water. -
imagery: we will compare positive against neutral imagery and negative against neutral imagery. -
gender: this variable has only two levels so a simple contrast will compare those identifying as male to those identifying as female.
The contrast options are shown in Figure 330.
Your output will show Mauchly’s sphericity test for each effect. The main effect of drink significantly violates the sphericity assumption (W = 0.572, p = .009) but the main effect of imagery and the imagery by drink interaction do not. However, as suggested in the book, it’s a good idea to correct for sphericity regardless of Mauchley’s test so that’s what we’ll do. The summary table of the repeated-measures effects (Figure 331) has been edited to show only Greenhouse-Geisser corrected degrees of freedom (the book explains how to do this). Basically everything is significant. However, the question specifically asks about the combined effect of imagery, drink and gender on ratings of the products so well focus on the three-way interaction. In short, there is a significant three-way drink × imagery × gender interaction, F(3.25, 58.52) = 3.70, p = .014.
The nature of this interaction is shown up in the means, which are plotted in Figure 332. The male plot shows that when positive imagery is used (circles), males generally rated all three drinks positively (the circles are higher than the other shapes for all drinks). This pattern is true of females also (the blue line/circles representing positive imagery are above the other two lines). When neutral imagery is used (light green line/squares), males rate beer very highly, but rate wine and water fairly neutrally. Females, on the other hand rate beer and water neutrally, but rate wine more positively (in fact, the pattern of the positive and neutral imagery lines show that women generally rate wine slightly more positively than water and beer). So, for neutral imagery males still rate beer positively, and females still rate wine positively. For the negative imagery (dark green line/triangles), the males still rate beer very highly, but give low ratings to the other two types of drink. So, regardless of the type of imagery used, males rate beer very positively (if you look at the plot you’ll note that ratings for beer are virtually identical for the three types of imagery). Females, however, rate all three drinks very negatively when negative imagery is used. The three-way interaction is, therefore, likely to reflect that males seem fairly immune to the effects of imagery when beer is being used as a stimulus, whereas females are not.
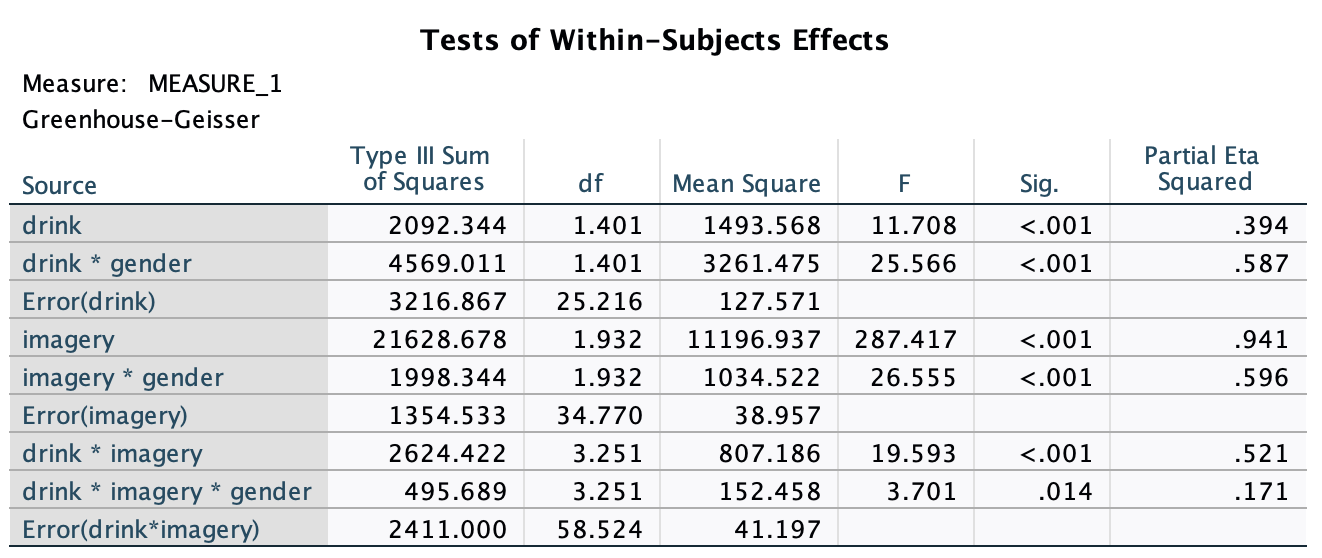
Warning: A numeric `legend.position` argument in `theme()` was deprecated in ggplot2
3.5.0.
ℹ Please use the `legend.position.inside` argument of `theme()` instead.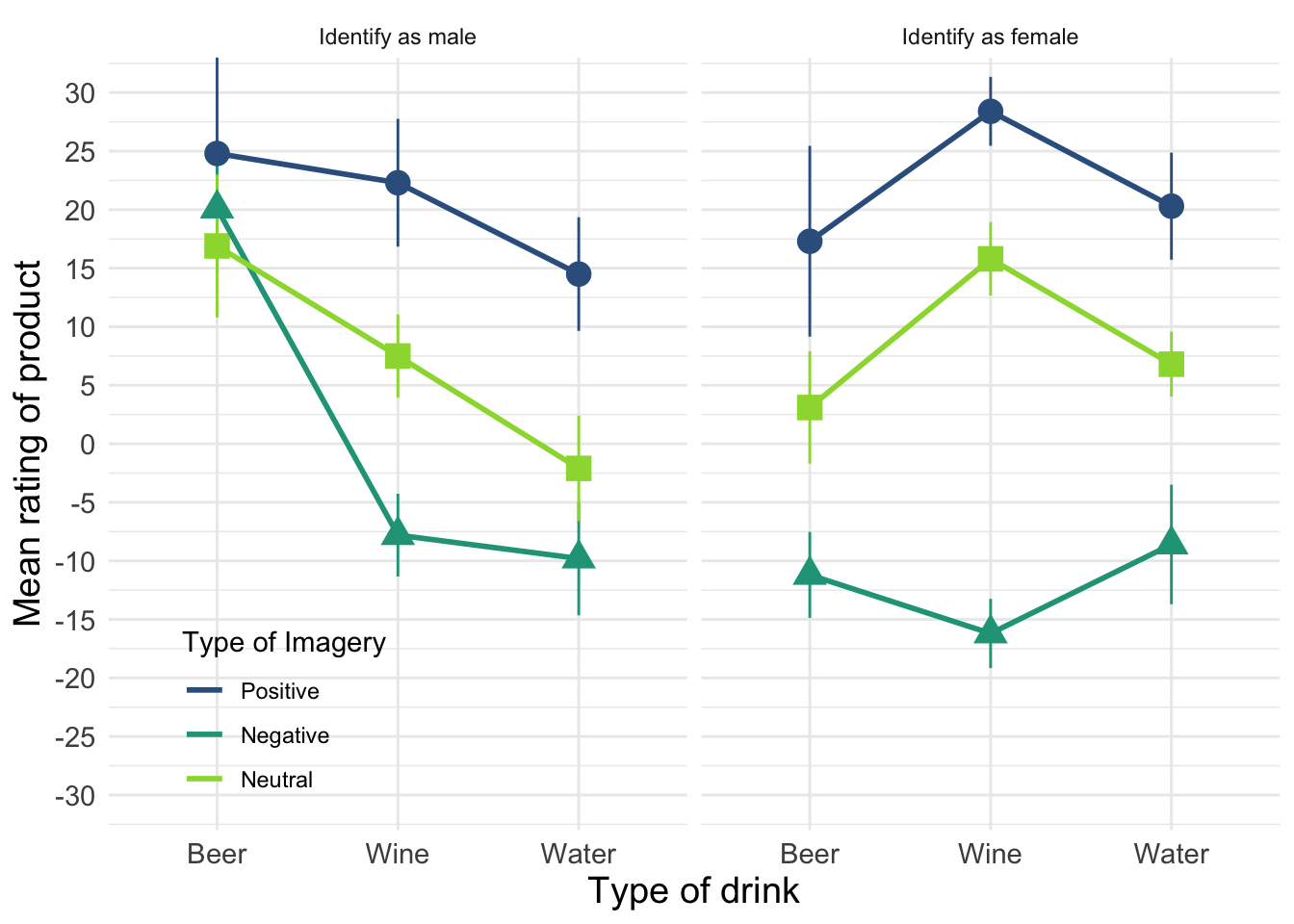
The contrasts (Figure 333) will show up exactly what this interaction represents.
- Drink × imagery × gender interaction 1: beer vs. water, positive vs. neutral imagery, male vs. female. The first interaction term compares level 1 of drink (beer) to level 3 (water), when positive imagery (level 1) is used compared to neutral (level 3) in males compared to females, F(1, 18) = 2.33, p = .144, \(\eta_p^2\) = 0.12. The non-significance of this contrast tells us that the difference in ratings when positive imagery is used compared to neutral imagery is roughly equal when beer is used as a stimulus and when water is used, and these differences are equivalent in male and female participants. With respect to Figure 332 it means that the distance between the circles and squares in the beer condition is the same as the distance between the circles and squares in the water condition and that these distances are equivalent in males and females.
- Drink × imagery × gender interaction 2: beer vs. water, negative vs. neutral imagery, male vs. female. The second interaction term looks at level 1 of drink (beer) compared to level 3 (water), when negative imagery (level 2) is used compared to neutral (level 3). This contrast is significant, F(1, 18) = 5.59, p = 0.029, \(\eta_p^2\) = 0.24. This result tells us that the difference in ratings between beer and water when negative imagery is used (compared to neutral imagery) is different between males and females. With respect to Figure 332 it means that the distance between the triangles and squares in the beer condition relative to the same distance for water was different in males and females.
- Drink × imagery × gender interaction 3: wine vs. water, positive vs. neutral imagery, male vs. female. The third interaction term looks at level 2 of drink (wine) compared to level 3 (water), when positive imagery (level 1) is used compared to neutral (level 3) in males compared to females. This contrast is non-significant, F(1, 18) = 0.03, p = 0.877, \(\eta_p^2\) = 0.001. This result tells us that the difference in ratings when positive imagery is used compared to neutral imagery is roughly equal when wine is used as a stimulus and when water is used, and these differences are equivalent in male and female participants. With respect to Figure 332 it means that the distance between the circles and squares in the wine condition is the same as the corresponding distance in the water condition and that these distances are equivalent in males and females.
- Drink × imagery × gender interaction 4: wine vs. water, negative vs. neutral imagery, male vs. female. The final interaction term looks at level 2 of drink (wine) compared to level 3 (water), when negative imagery (level 2) is used compared to neutral (level 3). This contrast is very close to significance, F(1, 18) = 4.38, p = .051, \(\eta_p^2\) = 0.196. This result tells us that the difference in ratings between wine and water when negative imagery is used (compared to neutral imagery) is different between men and women (although this difference has not quite reached significance). With respect to Figure 332 it means that the distance between the triangles and squares in the wine condition relative to the same distance for water was different (depending on how you interpret a p of 0.051) in males and females. It is noteworthy that this contrast was close to the 0.051 threshold. At best, this result is suggestive and not definitive.
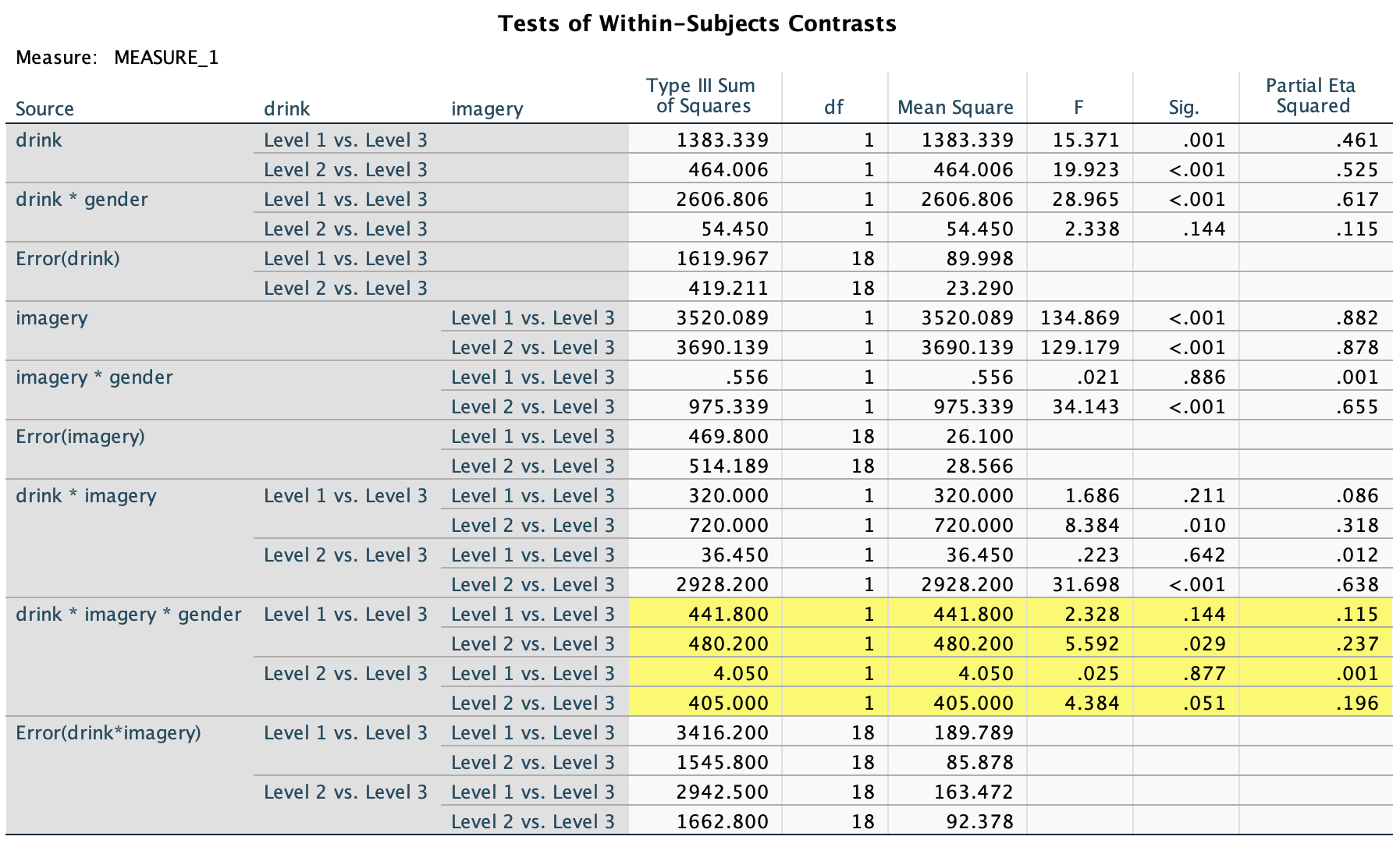
Task 16.2
Text messaging and Twitter encourage communication using abbreviated forms of words (if u no wat I mean). A researcher wanted to see the effect this had on children’s understanding of grammar. One group of 25 children was encouraged to send text messages on their mobile phones over a 6-month period. A second group of 25 was forbidden from sending text messages for the same period (to ensure adherence, this group were given armbands that administered painful shocks in the presence of a phone signal). The outcome was a score on a grammatical test (as a percentage) that was measured both before and after the experiment. The data are in the file
text_messages.sav. Does using text messages affect grammar?
Follow the general procedure and set up the initial dialog boxes as in Figure 334 and Figure 335 (for more detailed instructions see the book).
Because time has only two levels sphericity is not relevant to this model, so Figure 336 shows the results with sphericity assumed. The main effect of time is significant, so we can conclude that grammar scores were significantly affected by the time at which they were measured. The exact nature of this effect is easily determined because there were only two points in time (and so this main effect is comparing only two means). The main effect of group has a p-value of .09, which is just above the critical value of .05 (I’m assuming here that we’ve set alpha at 0.05), so there was no significant main effect on grammar scores of whether children text-messaged or not.
There is a significant interaction between the time at which grammar was measured and whether or not children were allowed to text-message within that time, F(1, 48) = 4.17, p = .047, \(\eta_p^2\) = 0.08. The mean ratings in all conditions help us to interpret this effect. Looking at the earlier interaction plot, we can see that although grammar scores fell in controls, the drop was much more marked in the text messagers; so, text messaging does seem to ruin your ability at grammar compared to controls. Figure 337 shows the mean grammar score (and 95% confidence interval) before and after the experiment for the text message group and the controls. It’s clear that in the text message group grammar scores went down over the six-month period whereas they remained fairly static for the controls.
The simple effects analysis (Figure 338), in combination with the means (Figure 337) indicate that grammar scores significantly decreased in the text message group, F(1, 48) = 17.84, p < 0.001, \(\eta_p^2\) = 0.27, but not the control group, F(1, 48) = 1.79, p = 0.19, \(\eta_p^2\) = 0.04.
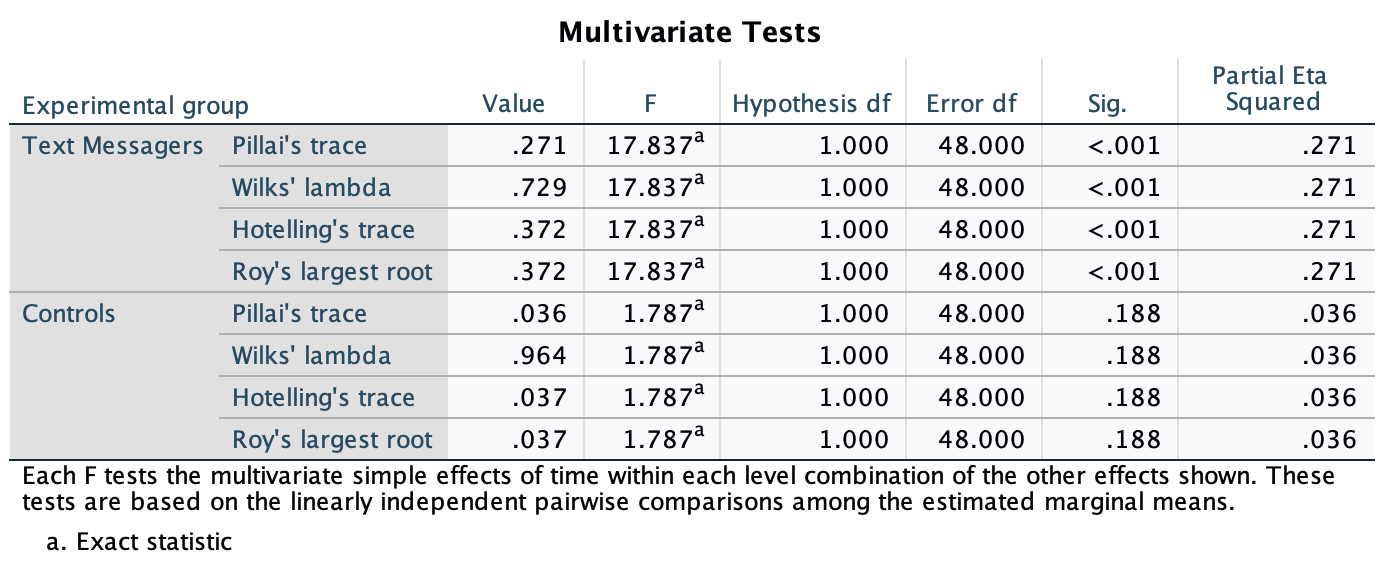
Task 16.3
A researcher hypothesized that reality TV show contestants start off with personality disorders that are exacerbated by being forced to spend time with people as attention-seeking as them (see Chapter 1). To test this hypothesis, she gave eight contestants a questionnaire measuring personality disorders before and after they entered the show. A second group of eight people were given the questionnaires at the same time; these people were short-listed to go on the show, but never did. The data are in
reality_tv.sav. Does entering a reality TV competition give you a personality disorder?
Follow the general procedure and set up the initial dialog boxes as in Figure 339 and Figure 340 (for more detailed instructions see the book).

Because time has only two levels sphericity is not relevant to this model, so Figure 341 shows the results with sphericity assumed. The main effect of time is not significant, so we can conclude that when we ignore group personality disorder scores did not change over time. The main effect of group was also not significant so when we ignore the time at which personality traits were measured contestants did not differ significantly from short listed candidates on personality disorder traits.
There is a significant interaction between the time at which personality disorders were measured and whether or not the participant was a contestant or short listed group, F(1, 14) = 7.15, p = 0.018, \(\eta_p^2\) = 0.34. The significant interaction seems to indicate that for controls PDS scores went down (slightly) from before entering the show to after leaving it, but for contestants these opposite is true: PDS scores increased over time (Figure 342). Simple effects analysis (Figure 343) indicated that personality disorder scores did not significantly change in short listed controls, F(1, 14) = 2.81, p = 0.116, \(\eta_p^2\) = 0.17, but came close to showing significant change in contestants, F(1, 14) = 4.44, p = 0.054, \(\eta_p^2\) = 0.24.
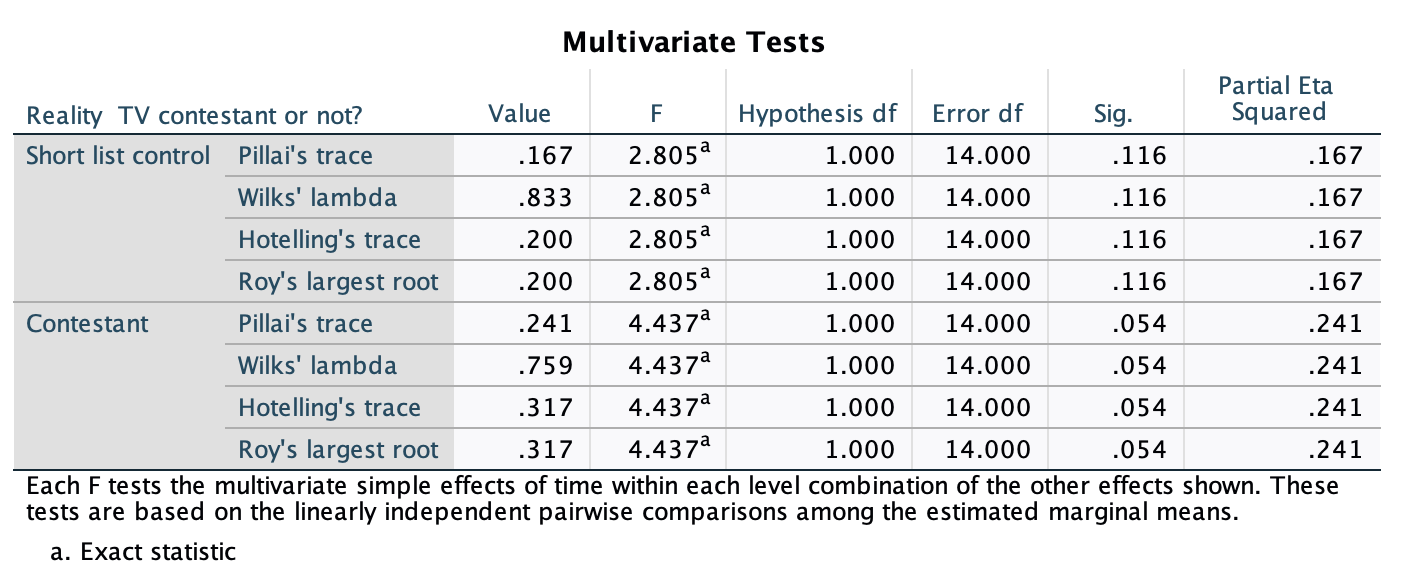
Task 16.4
Angry Birds is a video game in which you fire birds at pigs. A (fabricated) study was set up in which people played Angry Birds and a control game (Tetris) over a 2-year period (1 year per game). They were put in a pen of pigs for a day before the study, and after 1 month, 6 months and 12 months. Their violent acts towards the pigs were counted. Does playing Angry Birds make people more violent to pigs compared to a control game? (
angry_pigs.sav)
Follow the general procedure and set up the initial dialog boxes as in Figure 344 and Figure 345 (for more detailed instructions see the book). Get simple effects for the interaction as in Figure 346.
In keeping with the advice in the book, Figure 347 shows the results with the Greenhouse-Geisser corrections applied. The main effect of game was significant, indicating that (ignoring the time at which the aggression scores were measured), the type of game being played significantly affected participant’s aggression towards pigs. The main effect of time was also significant, so we can conclude that (ignoring the type of game being played), aggression was significantly different at different points in time. However, the effect that we are most interested in is the time × game interaction, which was also significant. This effect tells us that changes in aggression scores over time were different when participants played Tetris compared to when they played angry birds. Looking at Figure 348, we can see that for angry birds, aggression scores increase over time, whereas for Tetris, aggression scores decreased over time. The simple effects analysis (Figure 349) confirms this: for Tetris aggression to pigs does not significantly change over time, F(3, 80) = 1.35, p = 0.264, \(\eta_p^2\) = 0.05, but for angry pigs it does, F(3, 80) = 19.21, p = < 0.001, \(\eta_p^2\) = 0.43.
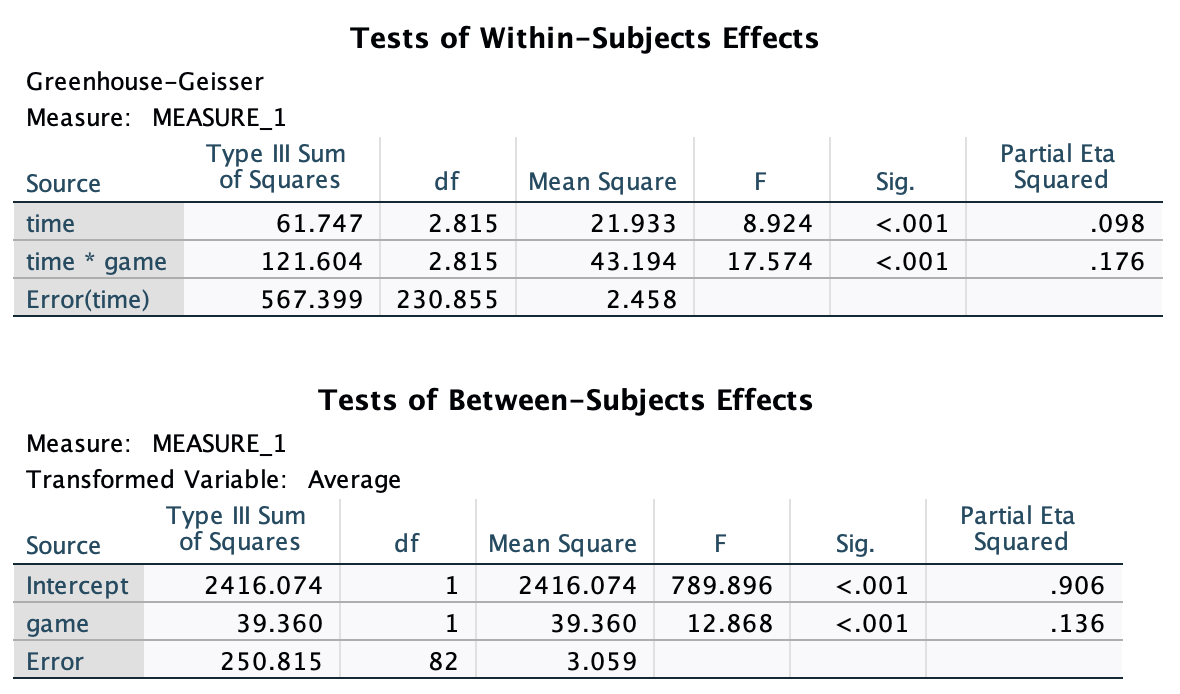
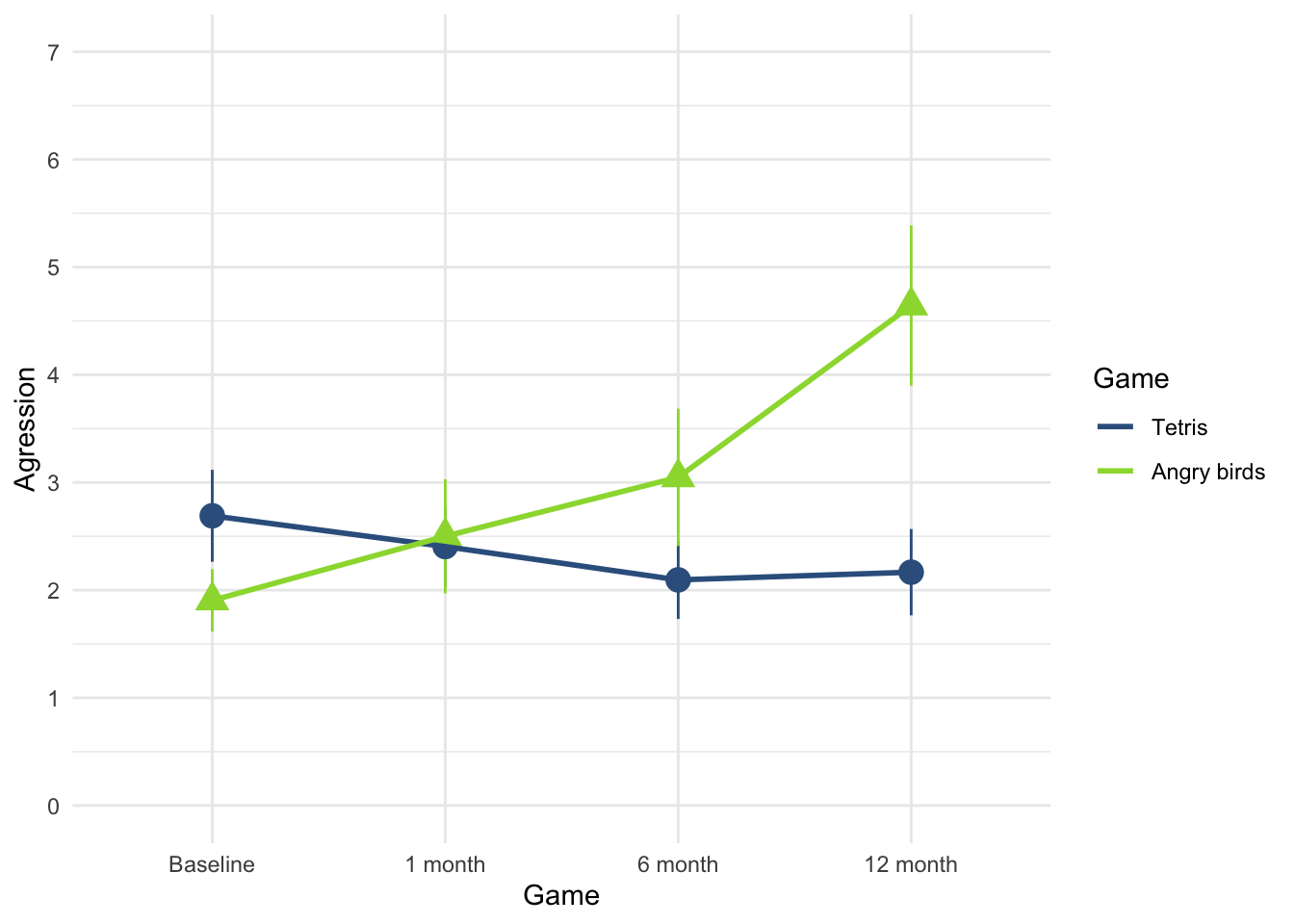
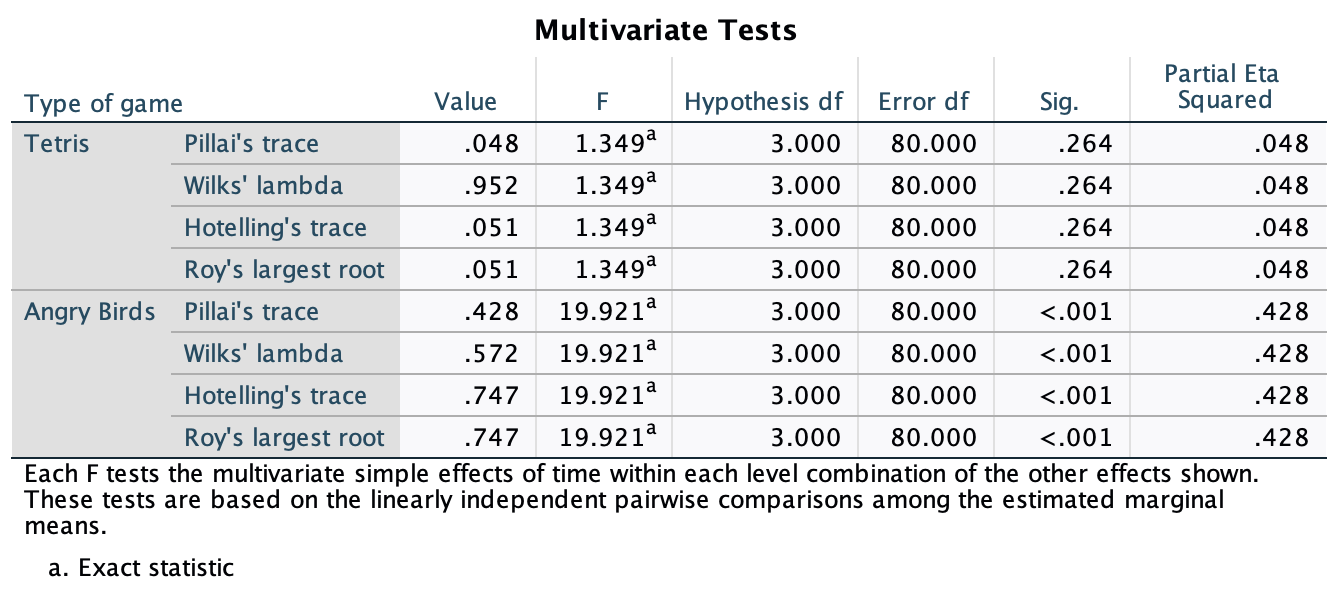
Task 16.5
A different study was conducted with the same design as in Task 4. The only difference was that the participant’s violent acts in real life were monitored before the study, and after 1 month, 6 months and 12 months. Does playing Angry Birds make people more violent in general compared to a control game? (
angry_real.sav)
Follow the general procedure and set up the initial dialog boxes as in Figure 344 and Figure 345 (basically you ruin the analysis in the same way as the previous task).
In keeping with the advice in the book, Figure 350 shows the results with the Greenhouse-Geisser corrections applied. The main effect of game was not significant, indicating that (ignoring the time at which the aggression scores were measured), the type of game being played did not significantly affected participant’s aggression in everyday life. The main effect of time was also not significant, so we can conclude that (ignoring the type of game being played), aggression was not significantly different at different points in time. However, the effect that we are most interested in is the time × game interaction, which was also not significant. This effect tells us that changes in aggression over time were comparable when participants played Tetris and Angry Birds. Looking at Figure 351, we can see that for both tetris and Angry Birds, aggression scores do not change over time (both lines are fairly flat).
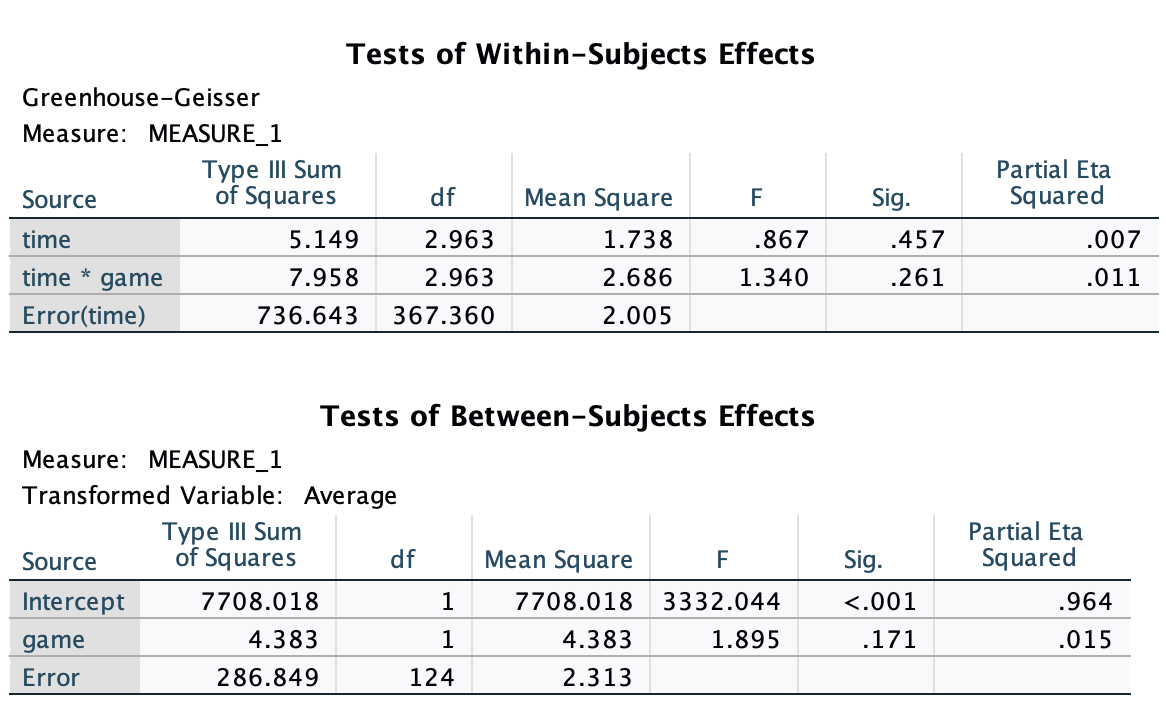

Task 16.6
My wife believes that she has received fewer friend requests from random men on Facebook since she changed her profile picture to a photo of us both. Imagine we took 40 women who had profiles on a social networking website; 17 of them had a relationship status of ‘single’ and the remaining 23 had their status as ‘in a relationship’ (
relationship_status). We asked these women to set their profile picture to a photo of them on their own (alone) and to count how many friend request they got from men over 3 weeks, then to switch it to a photo of them with a man (couple) and record their friend requests from random men over 3 weeks. Fit a model to see if friend requests are affected by relationship status and type of profile picture (profile_pic.sav).
Follow the general procedure and set up the initial dialog boxes as in Figure 352 and Figure 353 (for more detailed instructions see the book).
We have only two repeated-measures conditions here so sphericity is not an issue (see the book). The main effect of rel_status is significant, so we can conclude that, ignoring the type of profile picture, the number of friend requests was significantly affected by the relationship status of the woman. The exact nature of this effect is easily determined because there were only two levels of relationship status (and so this main effect is comparing only two means). If you look at Figure 355 single people always get more requests than those in a relationship (the circles are higher than the triangles)
The main effect of profile_picture is also significant. Therefore, when ignoring relationship status, there was a significant main effect of whether the person was alone in their profile picture or with a partner on the number of friend requests. If you look at Figure 355, the number of friend requests was higher when women were alone in their profile picture compared to when they were with a partner.
The interaction effect is the effect that we are most interested in and it is also significant (p = .010). We would conclude that there is a significant interaction between the relationship status of women and whether they had a photo of themselves alone or with a partner. From Figure 355 the significant interaction seems to indicate that when displaying a photo of themselves with a partner relationship status doesn’t have much impact on friend requests (the circle and triangle are in a similar location); however, when they are alone in their profile photo relationship status matters and they seem to get a lot more friend requests when single than when in a relationship (the circle a higher than the triangle). Simple effects analysis (Figure 356) confirms that there is a significant effect of relationship status when a womanwas single in her profile picture, F(1, 38) = 17.39, p < 0.001, \(\eta_p^2\) = 0.31, but not when she was pictured with a partner, F(1, 38) = 3.11, p = 0.086, \(\eta_p^2\) = 0.08.
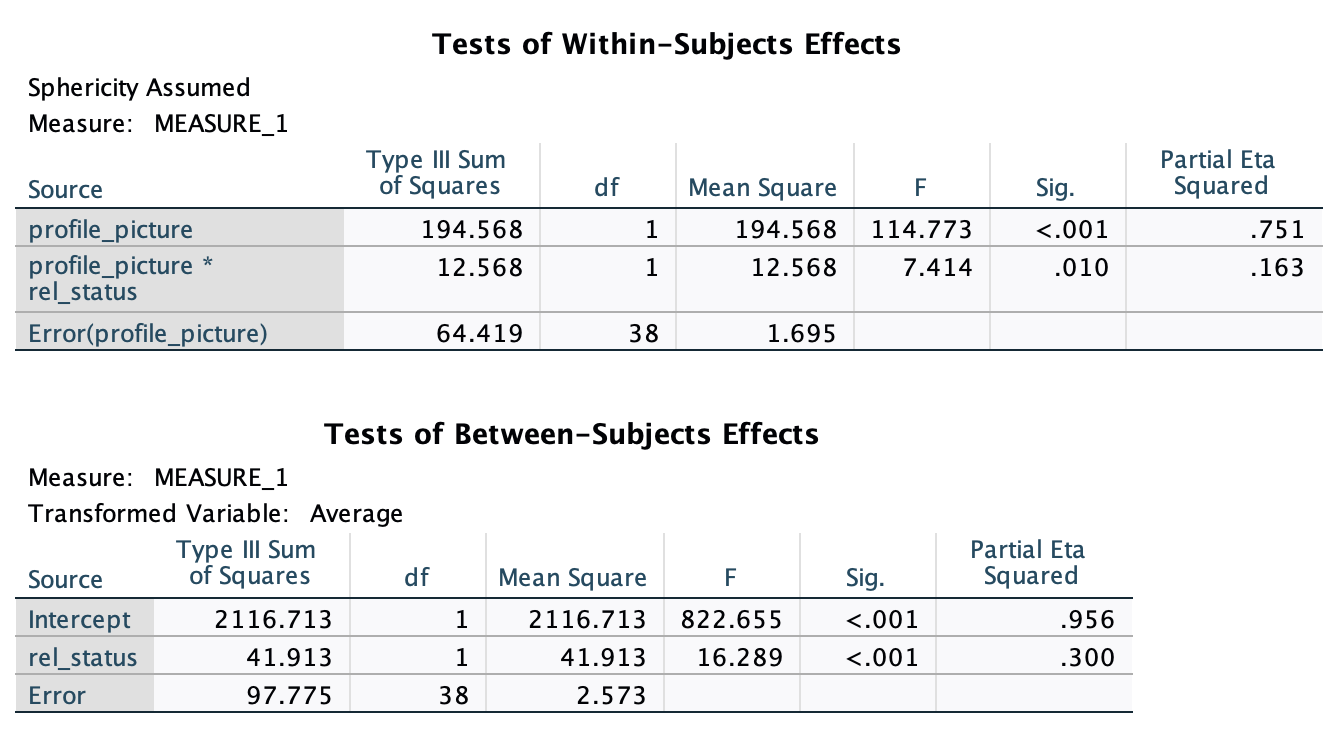
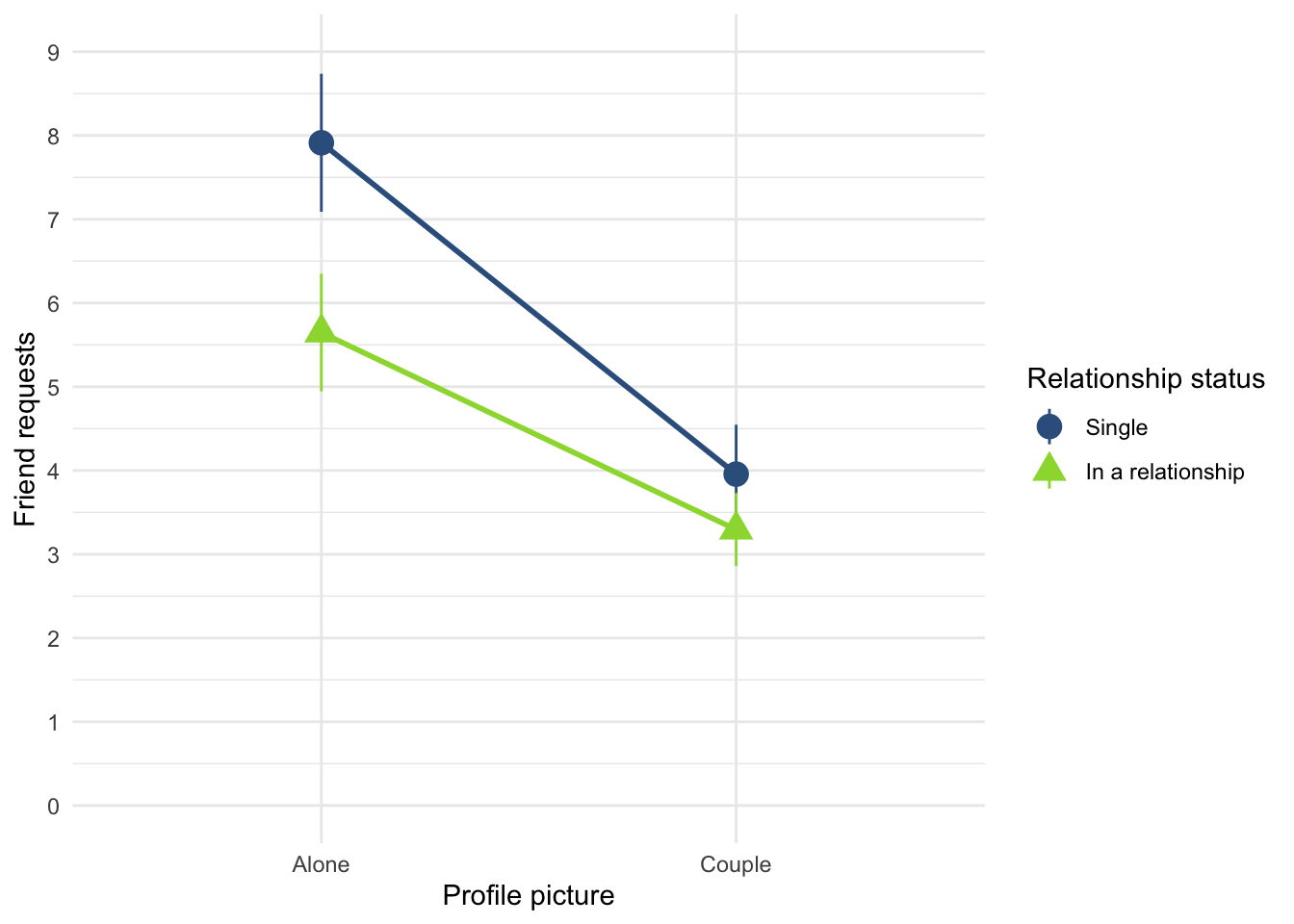
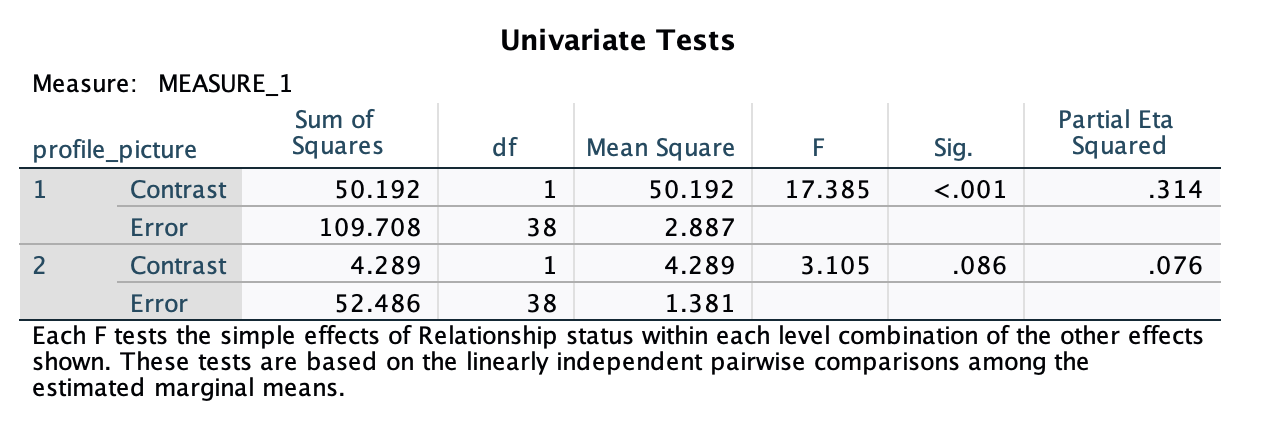
Task 16.7
Labcoat Leni’s Real Research 5.2 described a study in which researchers reasoned that if red was a proxy signal to indicate sexual proceptivity then men should find red female genitalia more attractive than other colours (Johns et al., 2012). They also recorded the men’s sexual experience (
partners) as ‘some’ or ‘very little’. Fit a model to test whether attractiveness was affected by genitalia colour (pale_pink,light_pink,dark_pink,red) and sexual experience (johns_2012.sav). Look at page 3 of Johns et al. to see how to report the results.
Follow the general procedure and set up the initial dialog boxes as in Figure 357 and Figure 358 (for more detailed instructions see the book). Because the theory predicted that red should be the most attractive colour I also asked fora simple contrast comparing each colour to red (Figure 359).
Generally in the book I suggest correcting using the Greenhouse-Geisser correction, but the authors report the multivariate tests, which is another appropriate way to deal with a lack of sphericity (because multivariate tests do not assume it). This information is in Figure 360. The main effect of colour is significant, F(3, 36) = 8.25, p < 0.001, \(\eta_p^2\) = 0.41, so we can conclude that, ignoring sexual experience, attractiveness ratings were significantly affected by the genital colour. The main effect of sexual experience was not significant, F(1, 38) = 0.48, p = 0.492, \(\eta_p^2\) = 0.01. Therefore, we can conclude that when ignoring genital colour, attractiveness ratings were not significantly different for those with ‘some’ compared to ‘very little’ sexual experience. The colour × Partners interaction is not significant, F(3, 36) = 2.75, p = 0.057, \(\eta_p^2\) = 0.19, suggesting that the effect of colour is not significantly moderated by sexual experience. Figure 361 shows this lack of interaction in that the lines are relatively parallel suggesting that the difference in attractiveness ratings for those with some sexual experience compared to those with very little is relatively similar for each colour (the distances between the circles and triangles are similar for each colour).
Given the interaction is not significant we can focus on interpreting the main effect of colour. The contrasts for the main effect of colour (Figure 362) show that attractiveness ratings were significantly lower when the colour was red compared to dark pink, F(1, 38) = 15.47, p < .001, light pink, F(1, 38) = 22.82, p < .001, and pale pink, F(1, 38) = 17.44, p < .001. This is contrary to the theory, which suggested that red would be rated as more attractive than other colours.
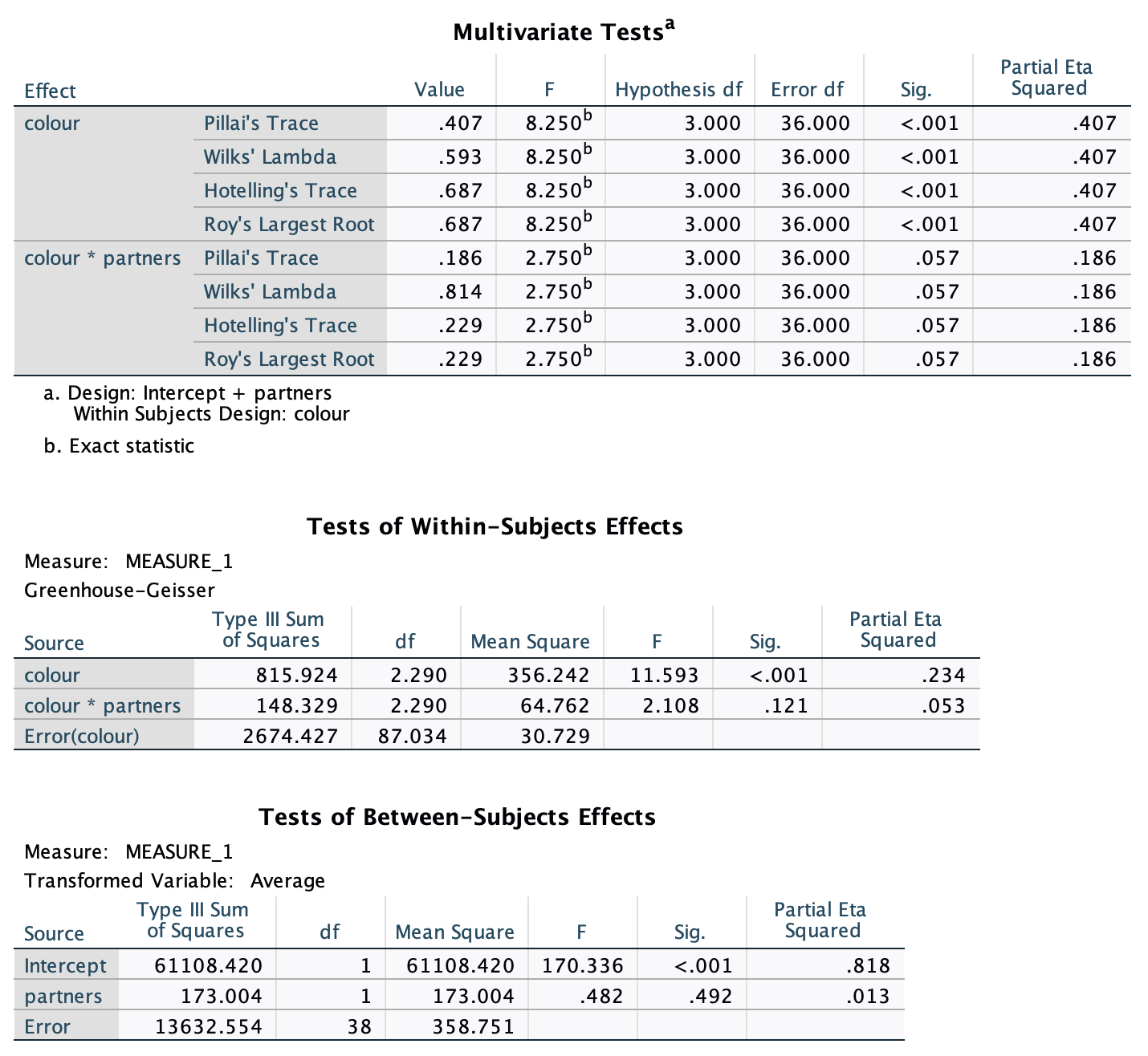
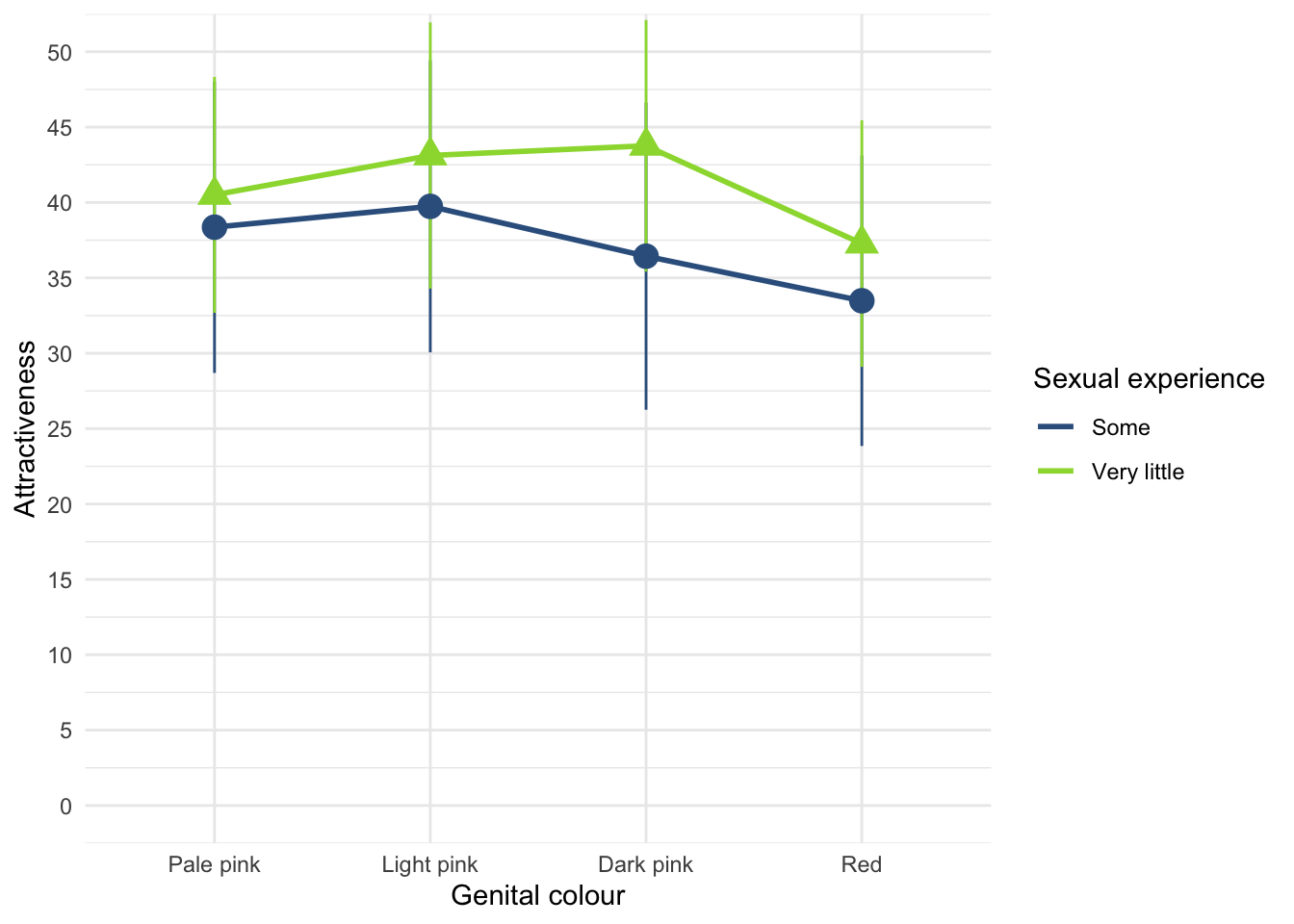
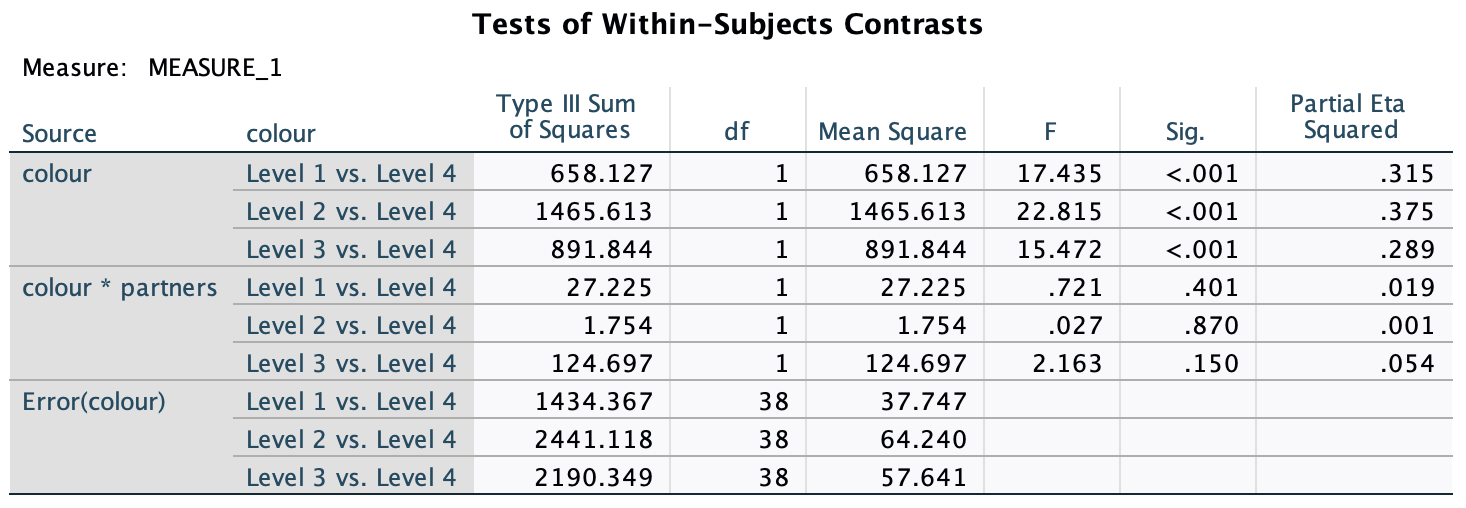
Chapter 17
Task 17.1
A farmyard psychologist decided to compare whether his chickens acted more like chickens than university lecturers did. He recorded 10 of his chickens as they went through a normal day, and did the same to 10 lecturers at the University of Sussex. He had two outcome measures: the number of chicken noises they made, and the quality of chicken noises (scored out of 10 by an independent farmyard noise expert). Use MANOVA and discriminant function analysis to find out whether these variables could be used to distinguish chickens from university lecturers (
chicken.sav).
To fit the model follow the general procedure. In this case
- Drag
qualityandquantityto the box labelled Dependent Variables andgroupto the area labelled Fixed Factors (Figure 363) - Click
 and select the options in Figure 364.
and select the options in Figure 364.
Follow up the analysis with discriminant function analysis. Drag quality and quantity to the box labelled Independents and group to the area labelled Grouping Variable. You will need to define the smallest and largest value for the groups, which in this case is 1 and 2 (Figure 366).
The descriptive statistics in Figure 369 suggest that chickens and Sussex lecturers do a fairly similar numbers of chicken impersonations (lecturers do slightly fewer actually, but they are of a higher quality).
Box’s test of the assumption of equality of covariance matrices tests the null hypothesis that the variance-covariance matrices are the same in both groups (Figure 370). For these data p is .000 (which is less than .05), hence, the covariance matrices are significantly different (the assumption is broken). However, because group sizes are equal we can ignore this test because Pillai’s trace should be robust to this violation (fingers crossed!).
All test statistics for the effect of group are significant with p = .032, which is less than .05 (Figure 371)). From this result we should probably conclude that the groups differ significantly in the quality and quantity of their chicken impersonations; however, this effect needs to be broken down to find out exactly what’s going on.
The univariate tests (Figure 372) of the main effect of group contains separate F-statistics for quality and quantity of chicken impersonations, respectively. The values of p indicate that there was a non-significant difference between groups in terms of both (p is greater than .05 in both cases). The multivariate test statistics led us to conclude that the groups did differ in terms of the quality and quantity of their chicken impersonations yet the univariate results contradict this!

To see how the dependent variables interact, we need to carry out a discriminant function analysis (DFA). The initial statistics from the DFA tell us that there was only one variate (because there are only two groups) and this variate is significant (Figure 373). Therefore, the group differences shown by the MANOVA can be explained in terms of one underlying dimension.
The standardized discriminant function coefficients tell us the relative contribution of each variable to the variates. Both quality and quantity of impersonations have similar-sized coefficients indicating that they have equally strong influence in discriminating the groups (Figure 374). However, they have the opposite sign, which suggests that that group differences are explained by the difference between the quality and quantity of impersonations.
The variate centroids for each group (Figure 375) confirm that variate 1 discriminates the two groups because the chickens have a negative coefficient and the Sussex lecturers have a positive one. There won’t be a combined-groups plot because there is only one variate.
Overall we could conclude that chickens are distinguished from Sussex lecturers in terms of the difference between the pattern of results for quantity of impersonations compared to quality. If we look at the means we can see that chickens produce slightly more impersonations than Sussex lecturers (but remember from the non-significant univariate tests that this isn’t sufficient, alone, to differentiate the groups), but the lecturers produce impersonations of a higher quality (but again remember that quality alone is not enough to differentiate the groups). Therefore, although the chickens and Sussex lecturers produce similar numbers of impersonations of similar quality (see univariate tests), if we combine the quality and quantity we can differentiate the groups.



Task 17.2
A news story claimed that children who lie would become successful citizens. I was intrigued because although the article cited a lot of well-conducted work by Dr. Khang Lee that shows that children lie, I couldn’t find anything in that research that supported the journalist’s claim that children who lie become successful citizens. Imagine a Huxleyesque parallel universe in which the government was daft enough to believe the contents of this newspaper story and decided to implement a systematic programme of infant conditioning. Some infants were trained not to lie, others were bought up as normal, and a final group was trained in the art of lying. Thirty years later, they collected data on how successful these children were as adults. They measured their
salary, and two indices out of 10 (10 = as successful as it could possibly be, 0 = better luck in your next life) of how successful theirfamilyandworklife was. Use MANOVA and discriminant function analysis to find out whether lying really does make you a better citizen (lying.sav)
To fit the model follow the general procedure. In this case
- Drag
salary,familyandworkto the box labelled Dependent Variables andlyingto the area labelled Fixed Factors (Figure 363) - Click
 and select the options in Figure 364.
and select the options in Figure 364.
Follow up the analysis with discriminant function analysis. Drag salary, family and work to the box labelled Independents and lying to the area labelled Grouping Variable. You will need to define the smallest and largest value for the groups, which in this case is 1 and 3.
The means (Figure 376) show that children encouraged to lie landed the best and highest-paid jobs, but had the worst family success compared to the other two groups. Children who were trained not to lie had great family lives but not so great jobs compared to children who were brought up to lie and children who experienced normal parenting. Finally, children who were in the normal parenting group (if that exists!) were pretty middle of the road compared to the other two groups.
Box’s test is non-significant, p = .345 (which is greater than .05), hence the covariance matrices are roughly equal as assumed (Figure 377).
In the main table of results (Figure 378) the column of real interest is the one containing the significance values of the F-statistics. For these data, Pillai’s trace (p = .002), Wilks’s lambda (p = .001), Hotelling’s trace (p < .001) and Roy’s largest root (p < .001) all reach the criterion for significance at the .05 level. Therefore, we can conclude that the type of lying intervention had a significant effect on success later on in life. The nature of this effect is not clear from the multivariate test statistic: it tells us nothing about which groups differed from which, or about whether the effect of lying intervention was on work life, family life, salary, or a combination of all three. To determine the nature of the effect, a discriminant analysis would be helpful, but for some reason SPSS provides us with univariate tests instead.
In Figure 379 the F-statistics for each univariate ANOVA and their significance values are listed in the columns labelled F and Sig. These values are identical to those obtained if one-way ANOVA was conducted on each dependent variable independently. As such, MANOVA offers only hypothetical protection of inflated Type I error rates: there is no real-life adjustment made to the values obtained. The values of p indicate that there was a significant difference between intervention groups in terms of salary (p = .049), family life (p = .004), and work life (p = .036). We should conclude that the type of intervention had a significant effect on the later success of children. However, this effect needs to be broken down to find out exactly what’s going on.
The contrasts (Figure 380) show that there were significant differences in salary (p = .016), family success (p = .002) and work success (p = .016) when comparing children who were prevented from lying (level 1) with those who were encouraged to lie (level 3). Looking back at the means, we can see that children who were trained to lie had significantly higher salaries, significantly better work lives but significantly less successful family lives when compared to children who were prevented from lying. When we compare children who experienced normal parenting (level 2) with those who were encouraged to lie (level 3), there were no significant differences between the three life success outcome variables (p > .05 in all cases).
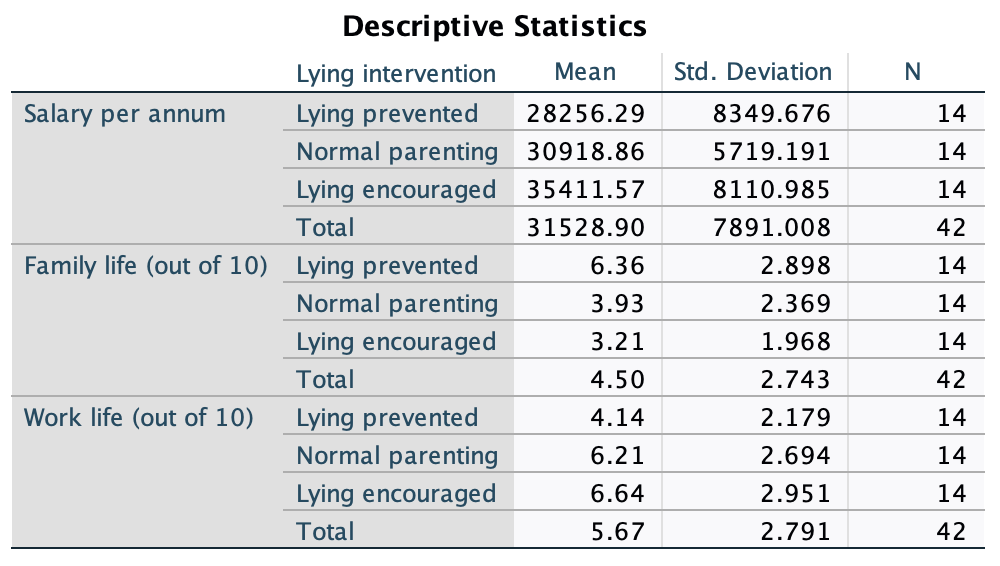

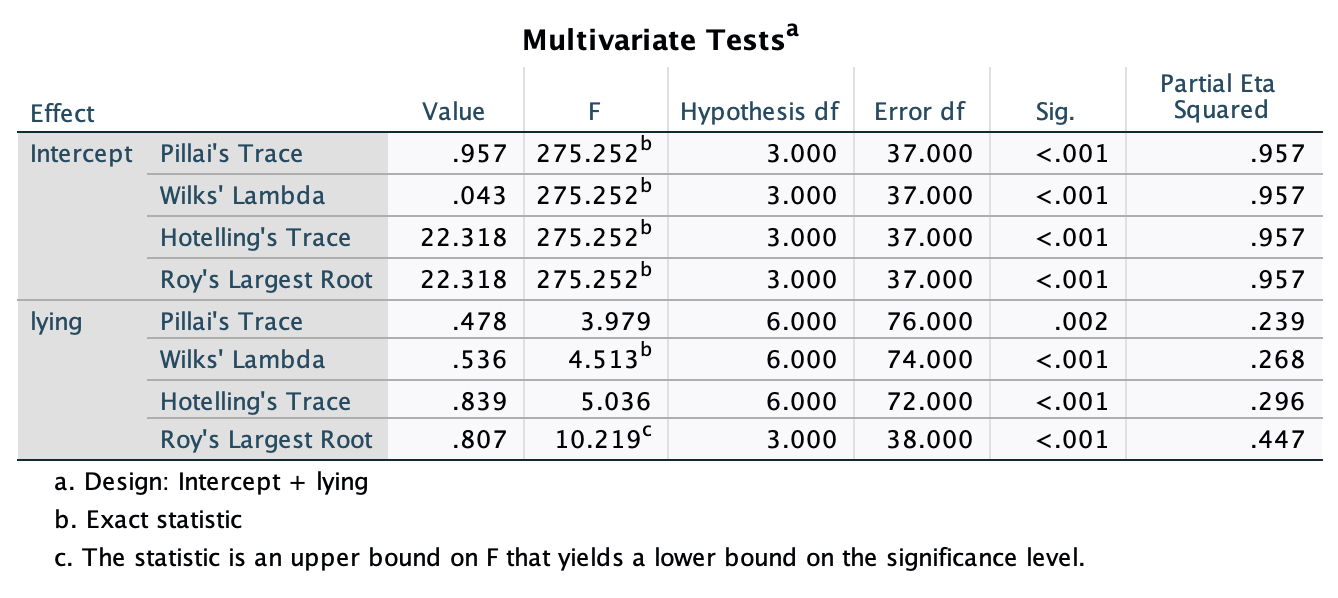
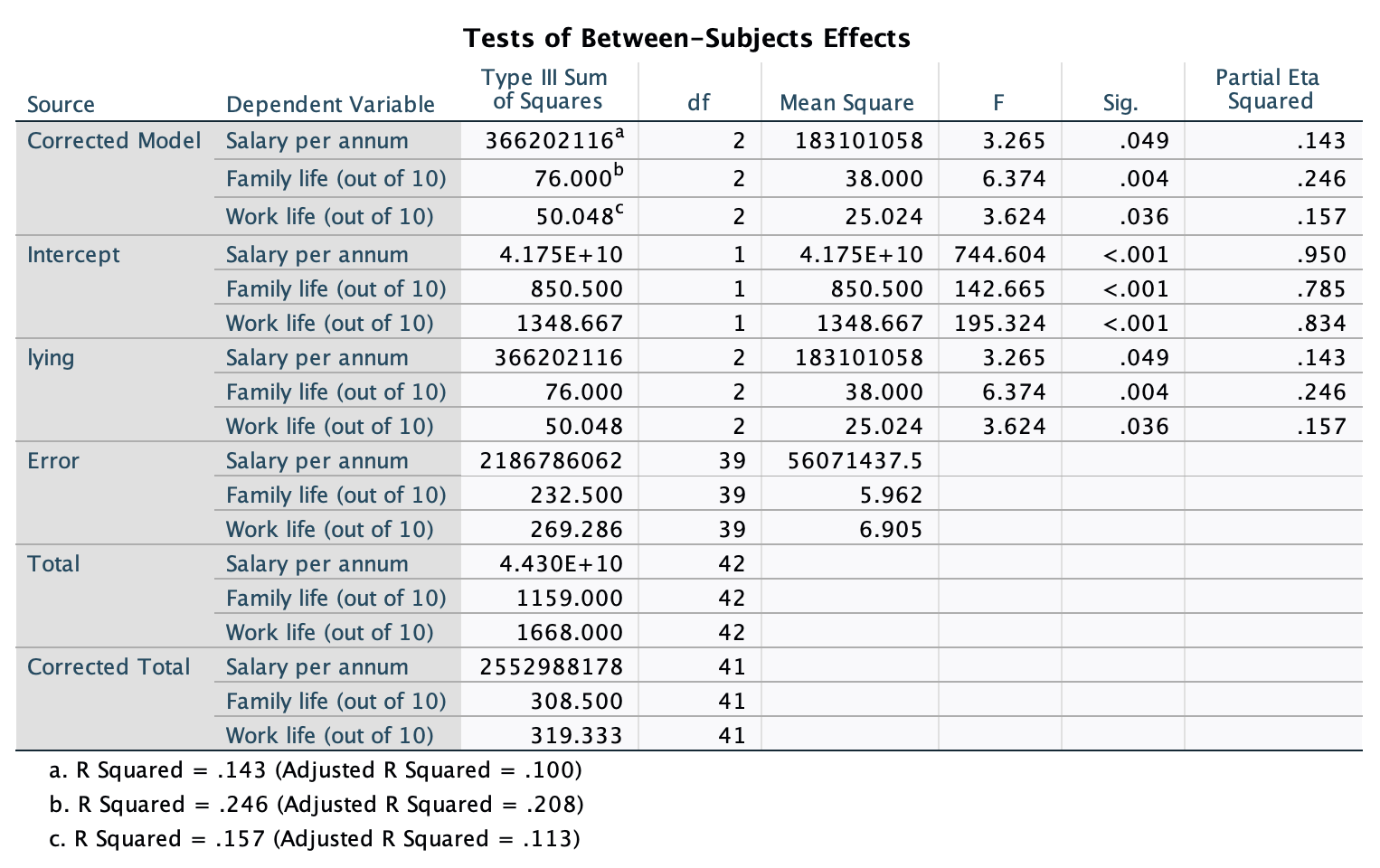
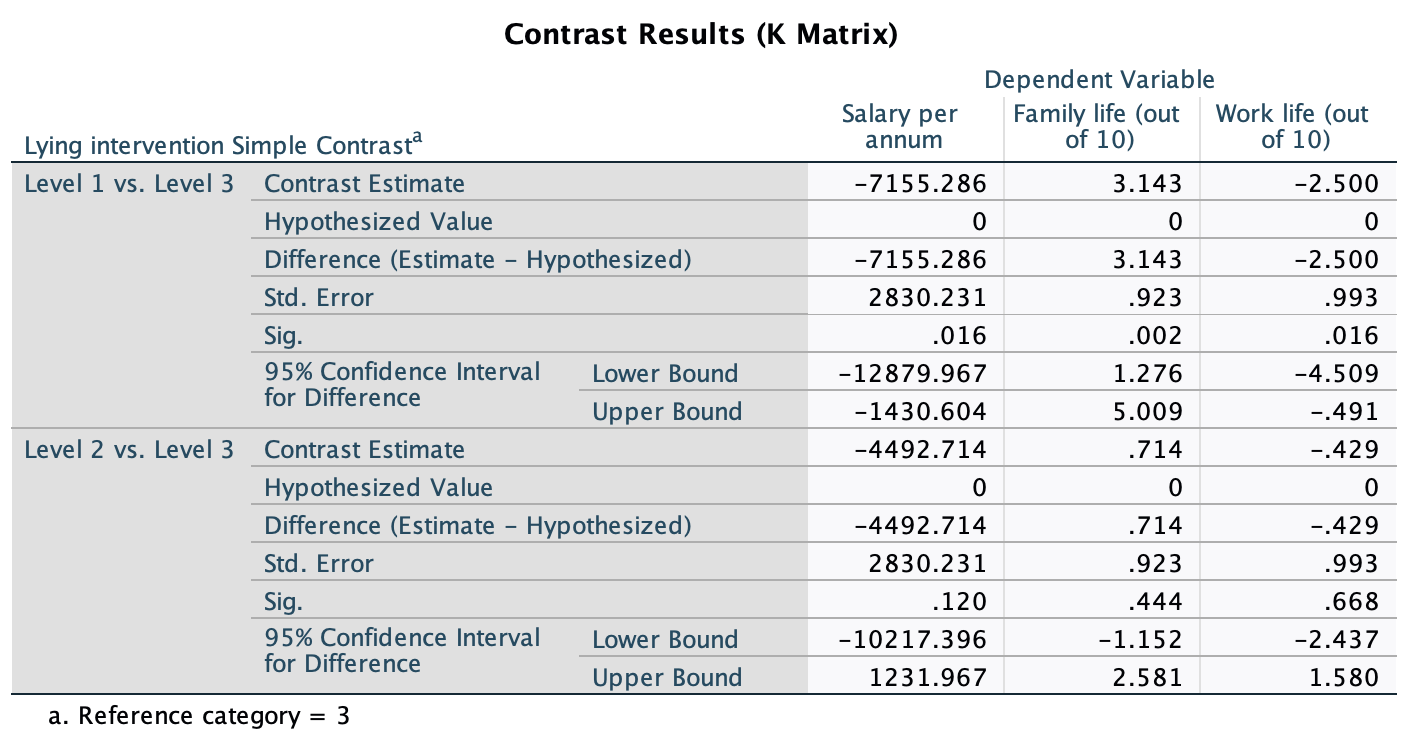
Let’s move onto the discriminant analysis. The covariance matrices are made up of the variances of each dependent variable for each group (Figure 381). The values in this output are useful because they give us some idea of how the relationship between dependent variables changes from group to group. For example, in the lying prevented group, all the dependent variables are positively related, so as one of the variables increases (e.g., success at work), the other two variables (family life and salary) increase also. In the normal parenting group, success at work is positively related to both family success and salary. However, salary and family success are negatively related, so as salary increases family success decreases and vice versa. Finally, in the lying encouraged group, salary has a positive relationship with both work success and family success, but success at work is negatively related to family success. It is important to note that these matrices don’t tell us about the substantive importance of the relationships because they are unstandardized - they merely give a basic indication.
The eigenvalues for each variate are converted into percentage of variance accounted for, and the first variate accounts for 96.1% of variance compared to the second variate, which accounts for only 3.9% (Figure 382). This table also shows the canonical correlation, which we can square to use as an effect size (just like \(R^2\), which we have encountered in the linear model).
Figure 383 shows the significance tests of both variates (‘1 through 2’ in the table), and the significance after the first variate has been removed (‘2’ in the table). So, effectively we test the model as a whole, and then peel away variates one at a time to see whether what’s left is significant. In this case with two variates we get only two steps: the whole model, and then the model after the first variate is removed (which leaves only the second variate). When both variates are tested in combination Wilks’s lambda has the same value (.536), degrees of freedom (6) and significance value (.001) as in the MANOVA. The important point to note from this table is that the two variates significantly discriminate the groups in combination (p = .001), but the second variate alone is non-significant, p = .543. Therefore, the group differences shown by the MANOVA can be explained in terms of two underlying dimensions in combination.
Figure 384 and Figure 385 are the most important for interpretation. The coefficients in these tables tell us the relative contribution of each variable to the variates. If we look at variate 1 first, family life has the opposite effect to work life and salary (work life and salary have positive relationships with this variate, whereas family life has a negative relationship). Given that these values (in both tables) can vary between 1 and 1, we can also see that family life has the strongest relationship, work life also has a strong relationship, whereas salary has a relatively weaker relationship to the first variate. The first variate, then, could be seen as one that differentiates family life from work life and salary (it affects family life in the opposite way to salary and work life). Salary has a very strong positive relationship to the second variate, family life has only a weak positive relationship and work life has a medium negative relationship to the second variate. This tells us that this variate represents something that affects salary and to a lesser degree family life in a different way than work life. Remembering that ultimately these variates are used to differentiate groups, we could say that the first variate differentiates groups by some factor that affects family differently than work and salary, whereas the second variate differentiates groups on some dimension that affects salary (and to a small degree family life) and work in different ways.
We can also use a combined-groups plot (Figure 386). This plot plots the variate scores for each person, grouped according to the experimental condition to which that person belonged. The plot (Figure 7) tell us that (look at the big squares) variate 1 discriminates the lying prevented group from the lying encouraged group (look at the horizontal distance between these centroids). The second variate differentiates the normal parenting group from the lying prevented and lying encouraged groups (look at the vertical distances), but this difference is not as dramatic as for the first variate. Remember that the variates significantly discriminate the groups in combination (i.e., when both are considered).
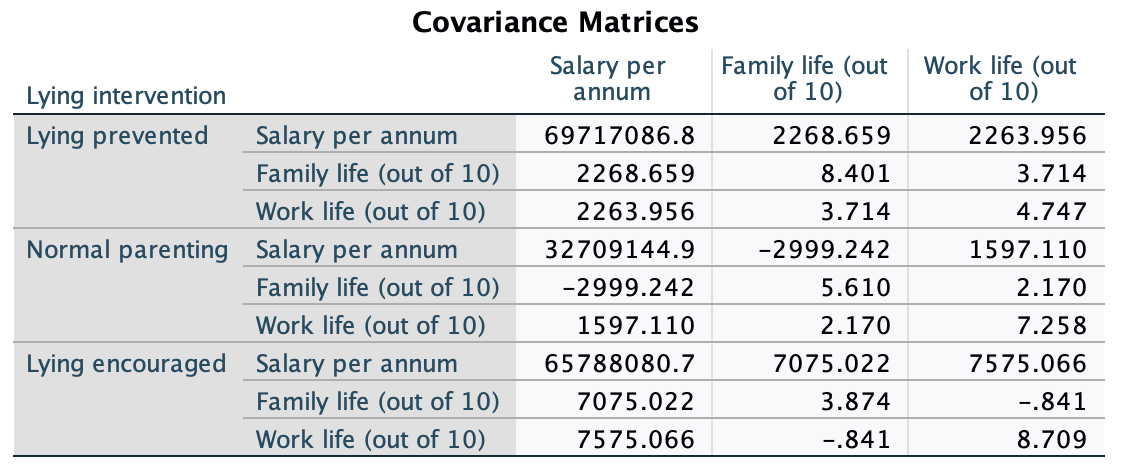
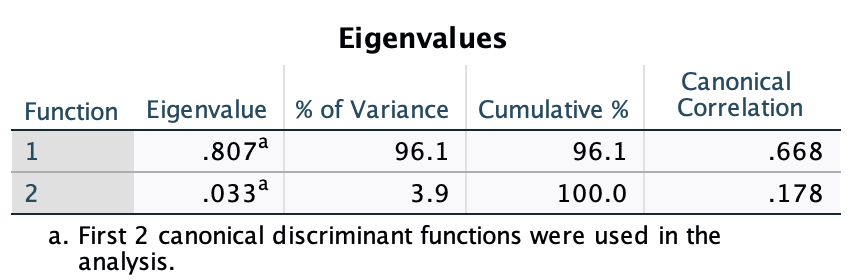
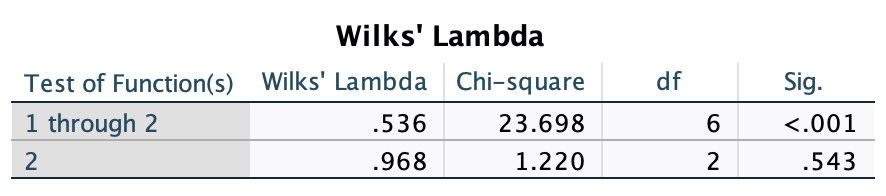
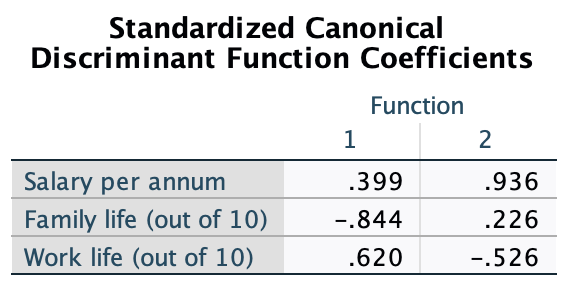
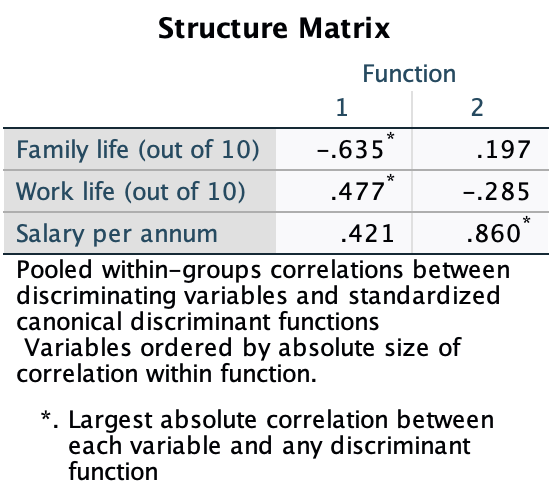
Task 17.3
I was interested in whether students’ knowledge of different aspects of psychology improved throughout their degree (
psychology.sav). I took a sample of first-years, second-years and third-years and gave them five tests (scored out of 15) representing different aspects of psychology:exper(experimental psychology such as cognitive and neuropsychology);stats(statistics);social(social psychology);develop(developmental psychology);person(personality). (1) Determine whether there are overall group differences along these five measures. (2) Interpret the scale-by-scale analyses of group differences. (3) Select contrasts that test the hypothesis that second- and third-years will score higher than first-years on all scales. (4) Select post hoc tests and compare these results to the contrasts. (5) Carry out a discriminant function analysis including only those scales that revealed group differences for the contrasts. Interpret the results.
To fit the model follow the general procedure. In this case
- Drag
exper,stats,social,developandpersonto the box labelled Dependent Variables andgroupto the area labelled Fixed Factors (Figure 363) - Click
 and select the options in Figure 364.
and select the options in Figure 364.
Follow up the analysis with discriminant function analysis. Drag exper, stats, social, develop and person to the box labelled Independents and group to the area labelled Grouping Variable. You will need to define the smallest and largest value for the groups, which in this case is 0 and 2.
Figure 387 contains the overall and group means and standard deviations for each dependent variable in turn. Box’s test has a p = .06 (which is greater than .05); hence, the covariance matrices are roughly equal and the assumption is tenable (Figure 388). (I mean, it’s probably not because it is close to significance in a relatively small sample.)
In Figure 389 the group effect tells us whether the scores from different areas of psychology differ across the three years of the degree programme. For these data, Pillai’s trace (p =.02), Wilks’s lambda (p = .012), Hotelling’s trace (p =.007) and Roy’s largest root (p =.01) all reach the criterion for significance of the .05 level. From this result we should probably conclude that the profile of knowledge across different areas of psychology does indeed change across the three years of the degree. The nature of this effect is not clear from the multivariate test statistic.
The univariate F-statistics (Figure 390) for each of the areas of psychology indicate that there was a non-significant difference between student groups in all areas (p > .05 in each case). The multivariate test statistics led us to conclude that the student groups did differ significantly across the types of psychology, yet the univariate results contradict this (I really should stop making up data sets that do this!).

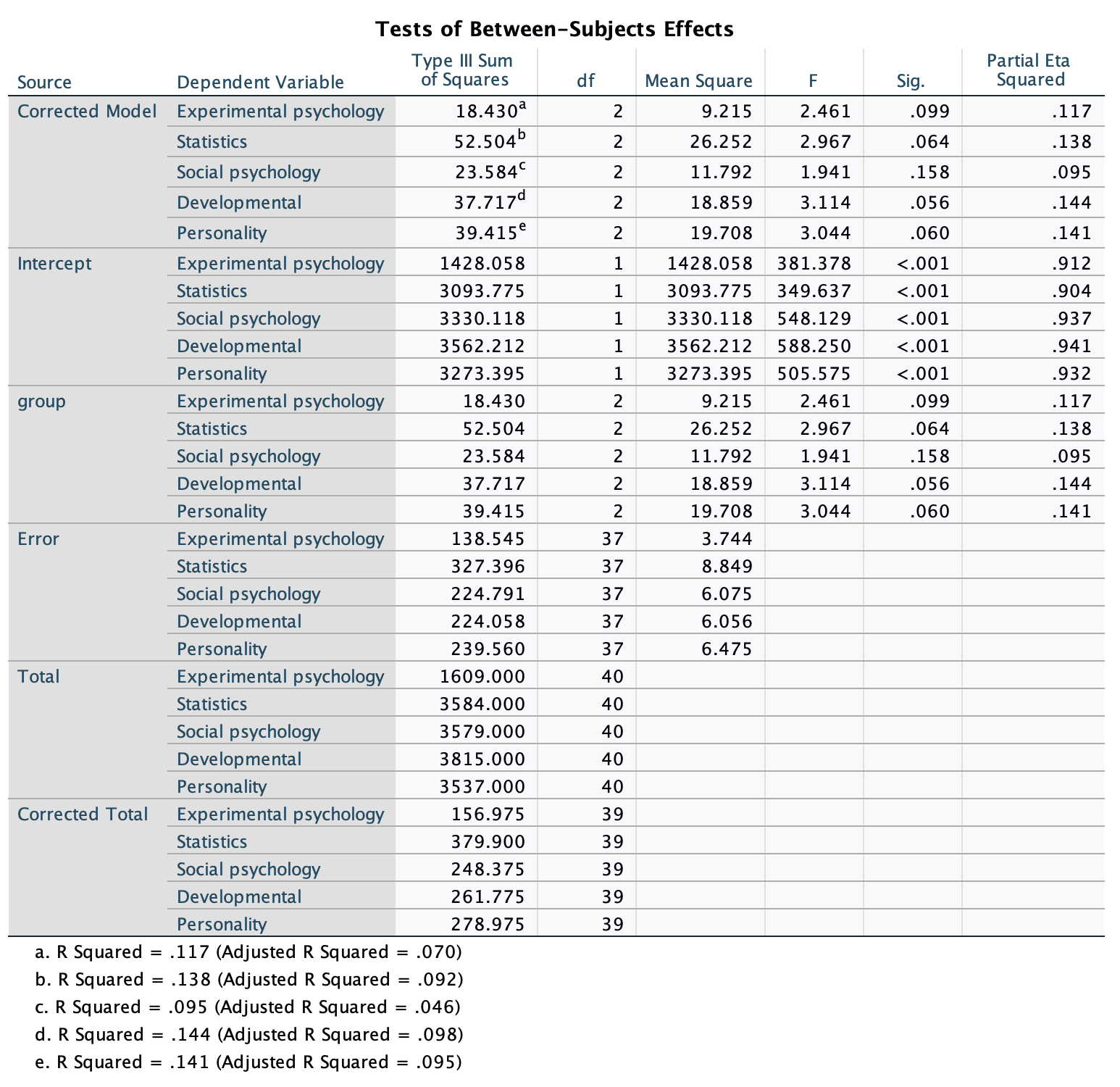
The initial statistics from the DFA (Figure 391) tell us that only one of the variates is significant (the second variate is non-significant, p = .608). Therefore, the group differences shown by the MANOVA can be explained in terms of one underlying dimension.
The standardized discriminant function coefficients (Figure 392) tell us the relative contribution of each variable to the variates. Looking at the first variate, it’s clear that statistic has the greatest contribution to the first variate. Most interesting is that on the first variate, statistics and experimental psychology have positive weights, whereas social, developmental and personality have negative weights. This suggests that the group differences are explained by the difference between experimental psychology and statistics compared to other areas of psychology.
The variate centroids for each group (Figure 393) tell us that variate 1 discriminates the first years from second and third years because the first years have a negative value whereas the second and third years have positive values on the first variate.
The relationship between the variates and the groups is best illuminated using a combined-groups plot (Figure 394), which plots the variate scores for each person, grouped according to the year of their degree. In addition, the group centroids are indicated, which are the average variate scores for each group. The plot for these data confirms that variate 1 discriminates the first years from subsequent years (look at the horizontal distance between these centroids).
Overall we could conclude that different years are discriminated by different areas of psychology. In particular, it seems as though statistics and aspects of experimentation (compared to other areas of psychology) discriminate between first-year undergraduates and subsequent years. From the means, we could interpret this as first years struggling with statistics and experimental psychology (compared to other areas of psychology) but with their ability improving across the three years. However, for other areas of psychology, first years are relatively good but their abilities decline over the three years. Put another way, psychology degrees improve only your knowledge of statistics and experimentation.
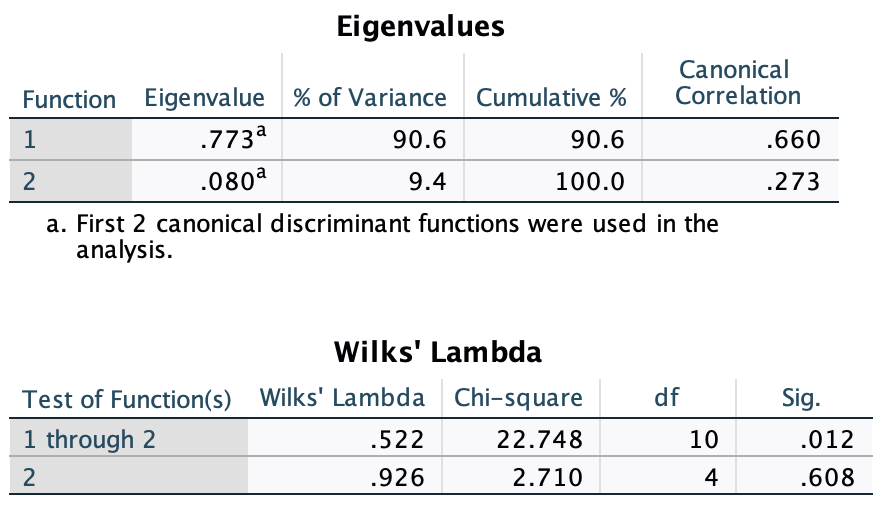
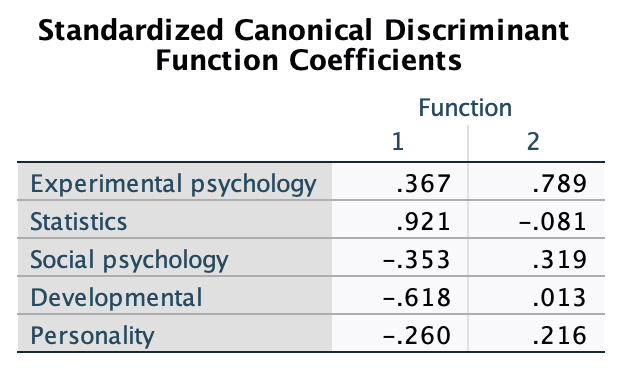
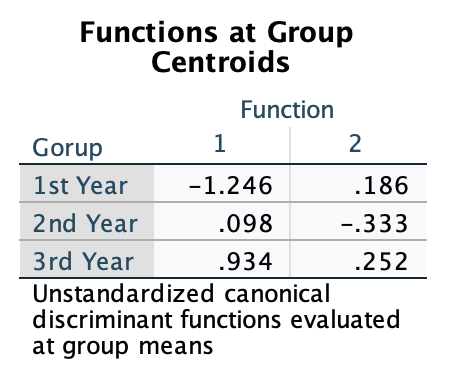
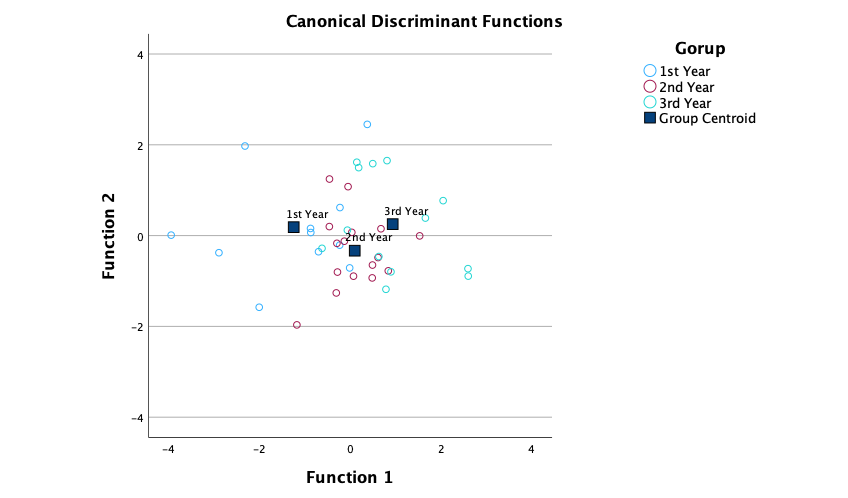
Chapter 18
Task 18.1
Rerun the analysis in this chapter using principal component analysis and compare the results to those in the chapter. (Set the iterations to convergence to 30.)
Follow the instructions in the chapter, except that in the Extraction dialog box select Principal components in the drop-down menu labelled Method, as shown in Figure 395
The question also suggests increasing the iterations to convergence to 30, and we do this in the Rotation dialog box as in Figure 396.
Note that I have selected an oblique rotation (Direct Oblimin) because (as explained in the book) it is unrealistic to assume that components measuring different aspects of a psychological construct will be independent. Complete all of the other dialog boxes as in the book.
Alternatively you can get this analysis using the following syntax
FACTOR
/VARIABLES question_01 question_02 question_03 question_04 question_05 question_06 question_07 question_08 question_09 question_10 question_11 question_12 question_13 question_14 question_15 question_16 question_17 question_18 question_19 question_20 question_21 question_22 question_23
/MISSING LISTWISE
/ANALYSIS question_01 question_02 question_03 question_04 question_05 question_06 question_07 question_08 question_09 question_10 question_11 question_12 question_13 question_14 question_15 question_16 question_17 question_18 question_19 question_20 question_21 question_22 question_23
/PRINT UNIVARIATE INITIAL CORRELATION SIG DET KMO INV REPR AIC EXTRACTION ROTATION
/FORMAT SORT BLANK(.30)
/PLOT EIGEN
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/CRITERIA KAISER ITERATE(30) DELTA(0)
/ROTATION OBLIMIN
/METHOD=CORRELATION.All of the descriptives, correlation matrices, KMO tests and so on should be exactly the same as in the book (these will be unaffected by our choice of principal components as the method of dimension reduction). Follow the book to interpret these.
Things start to get different at the point of extraction. The first part of the factor extraction process is to determine the linear components (note, linear components not factors) within the data (the eigenvectors) by calculating the eigenvalues of the R-matrix. There are as many components (eigenvectors) in the R-matrix as there are variables, but most will be unimportant. The eigenvalue tells us the importance of a particular vector. We can then apply criteria to determine which components to retain and which to discard. By default IBM SPSS Statistics uses Kaiser’s criterion of retaining components with eigenvalues greater than 1 (see the book for details).
The output (Figure 397) lists the eigenvalues associated with each linear component before extraction, after extraction and after rotation. Before extraction, 23 linear components are identified within the data (i.e., the number of original variables). The eigenvalues represent the variance explained by a particular linear component, and this value is also displayed as the percentage of variance explained (so component 1 explains 31.696% of total variance). The first few components explain relatively large amounts of variance (especially component 1), whereas subsequent components explain only small amounts of variance. The four components with eigenvalues greater than 1 are then extracted. The eigenvalues associated with these components are again displayed (and the percentage of variance explained) in the columns labelled Extraction Sums of Squared Loadings. The values in this part of the table are the same as the values before extraction, except that the values for the discarded components are ignored (i.e., the table is blank after the fourth component). The final part of the table (labelled Rotation Sums of Squared Loadings) shows the eigenvalues of the components after rotation. Rotation has the effect of optimizing the component structure, and for these data it has equalized the relative importance of the four components. Before rotation, component 1 accounted for considerably more variance than the remaining three (25.47% compared to 8.64%, 6.79% and 5.43%), but after rotation it accounts for only 4.52% of variance (compared to 3.47%, 3.37% and 3.17%, respectively).
The next output (Figure 398) shows the communalities before and after extraction. Remember that the communality is the proportion of common variance within a variable. Principal component analysis works on the initial assumption that all variance is common; therefore, before extraction the communalities are all 1 (see the column labelled Initial). In effect, all of the variance associated with a variable is assumed to be common variance. Once components have been extracted, we have a better idea of how much variance is, in reality, common. The communalities in the column labelled Extraction reflect this common variance. So, for example, we can say that 26.1% of the variance associated with question 1 is common, or shared, variance. Another way to look at these communalities is in terms of the proportion of variance explained by the underlying components. Before extraction, there are as many components as there are variables, so all variance is explained by the components and communalities are all 1. However, after extraction some of the components are discarded and so some information is lost. The retained components cannot explain all of the variance present in the data, but they can explain some. The amount of variance in each variable that can be explained by the retained components is represented by the communalities after extraction.
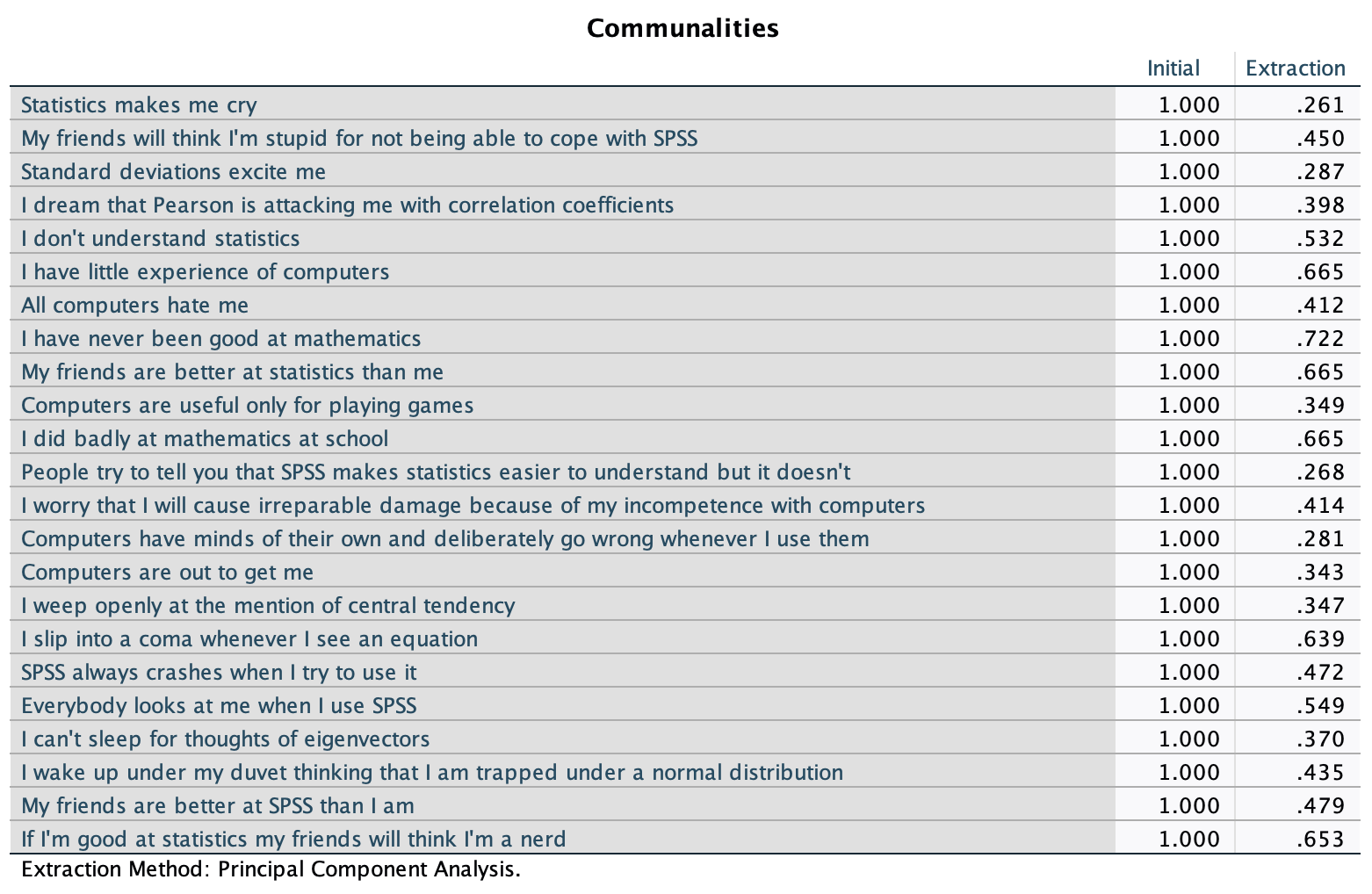
Figure 399 shows the component matrix before rotation. This matrix contains the loadings of each variable onto each component. By default IBM SPSS Statistics displays all loadings; however, if you followed the book you’d have requested that all loadings less than 0.3 be suppressed and so there are blank spaces. This doesn’t mean that the loadings don’t exist, merely that they are smaller than 0.3. This matrix is not particularly important for interpretation, but it is interesting to note that before rotation most variables load highly onto the first component.
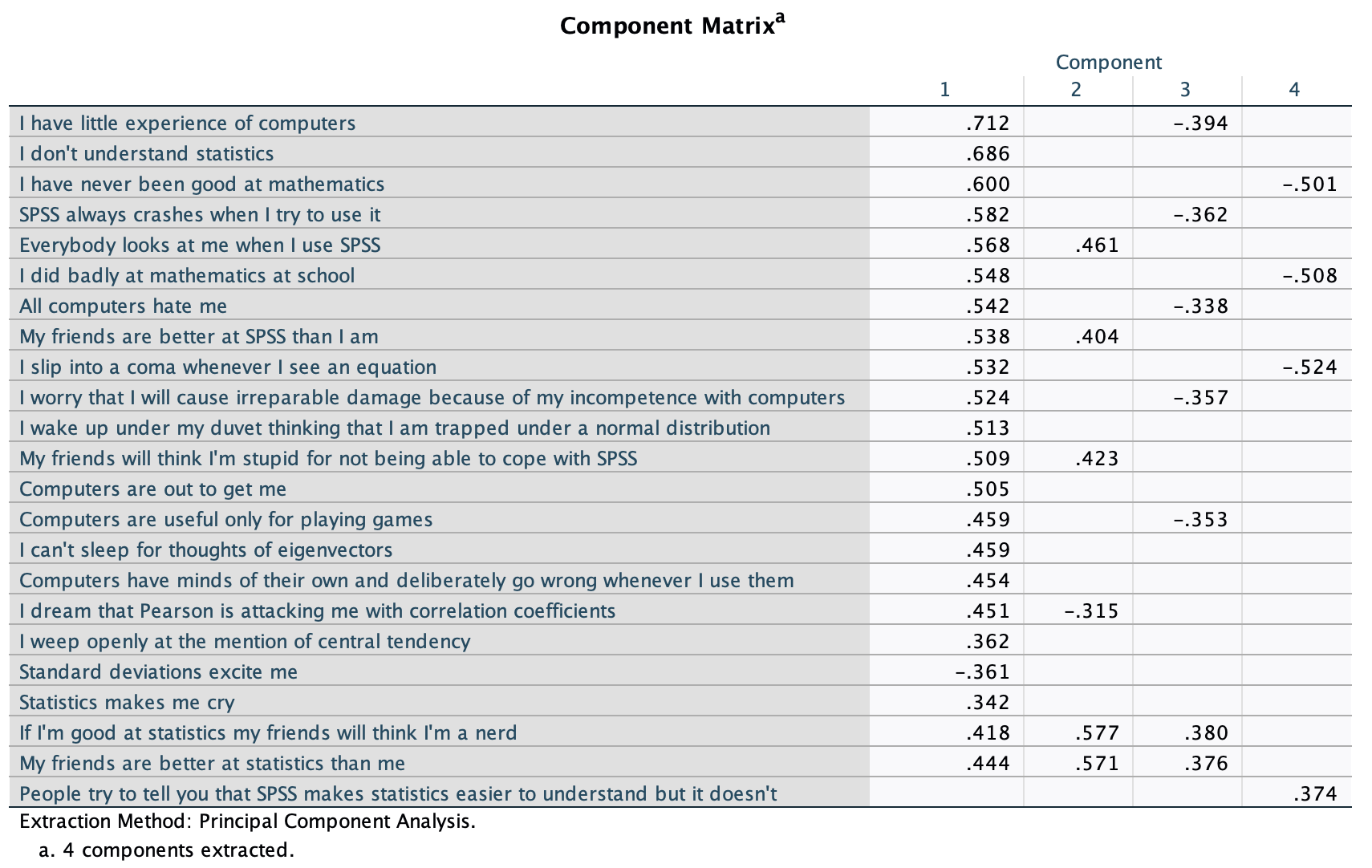
At this stage IBM SPSS Statistics has extracted four components based on Kaiser’s criterion. This criterion is accurate when there are fewer than 30 variables and communalities after extraction are greater than 0.7, or when the sample size exceeds 250 and the average communality is greater than 0.6. The communalities are shown in (Figure 398) and only one exceeds 0.7. The average of the communalities is 10.656/23 = 0.46. Therefore, on both grounds Kaiser’s rule might not be accurate. However, you should consider the huge sample that we have, because the research into Kaiser’s criterion gives recommendations for much smaller samples.
The scree plot (Figure 400) looks very similar to the one in the book (where we used principal axis factoring). The book gives more explanation, but essentially we could probably justify retaining either two or four components. As in the chapter we’ll stick with four.
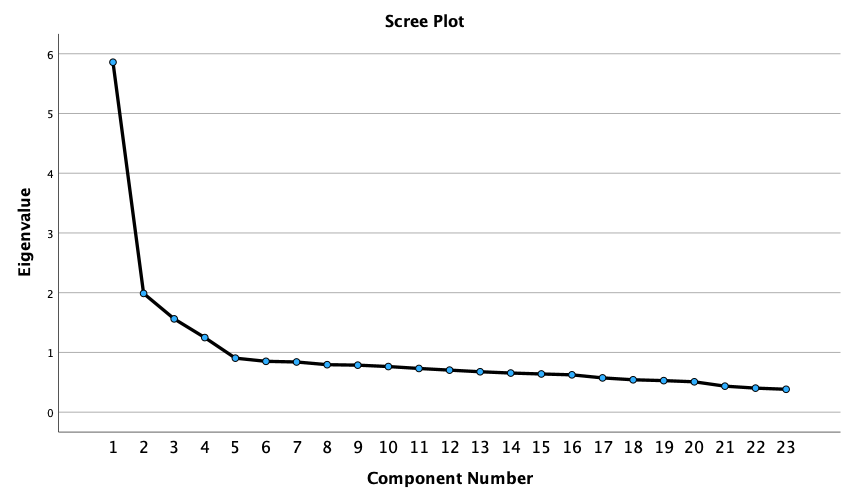
The next outputs shows the pattern (Figure 401) and structure matrices (Figure 402), which contain the component loadings for each variable onto each component (see the chapter for an explanation of the differences between these matrices). Let’s interpret the pattern matrix, because it’s a bit more straighforward. Remember that we suppressed loadings less than 0.3, so the blank spaces represent loadings lower than this threshold. Also, the variables are listed in the order of size of their component loadings (because we selected this option, by default they will be listed in the order you list them in the main dialog box).
Compare this matrix to the unrotated solution from earlier. Before rotation, most variables loaded highly onto the first component and the remaining components didn’t really get a look in. The rotation of the component structure has clarified things considerably: there are four components and variables generally load highly onto only one component and less so on the others.
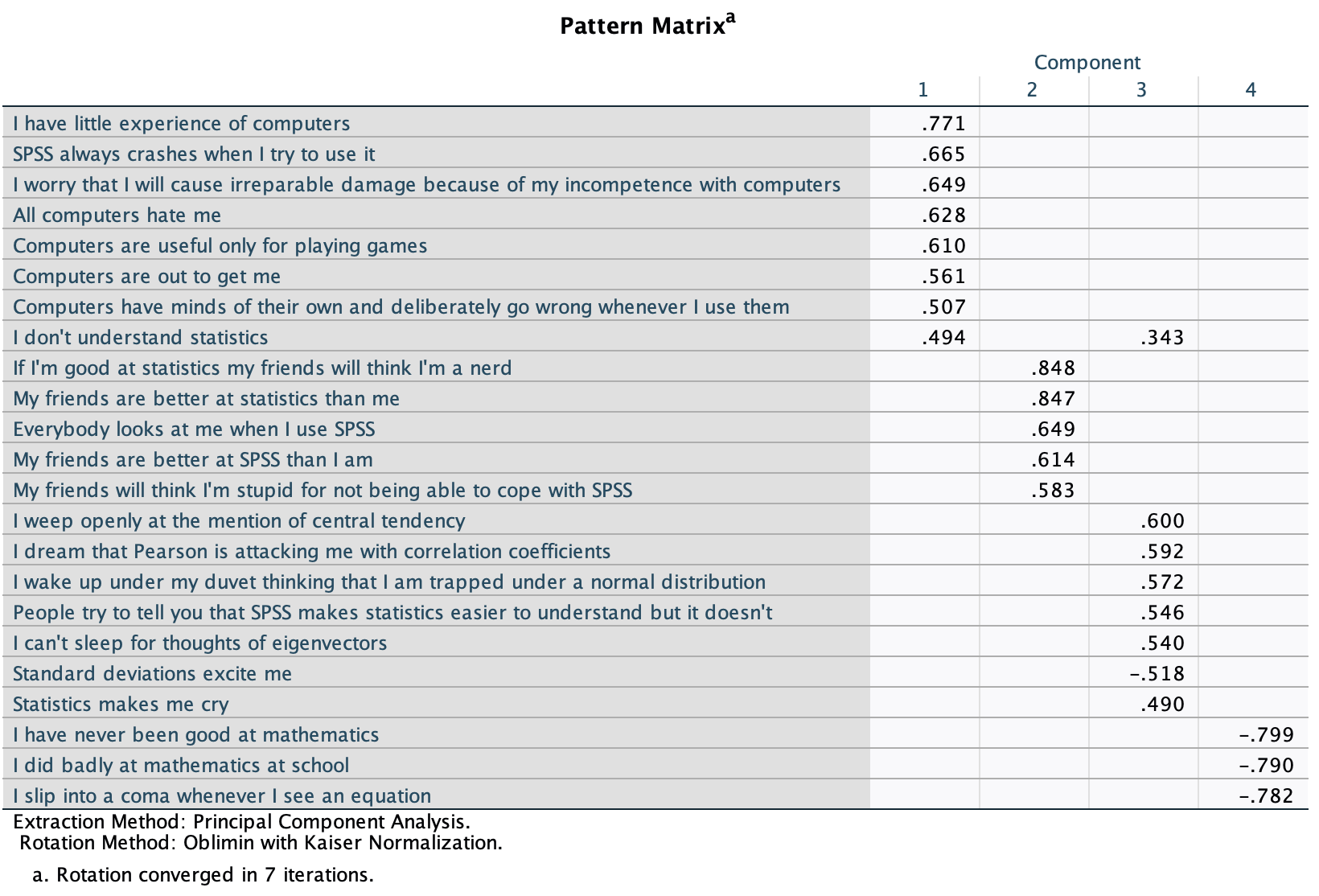
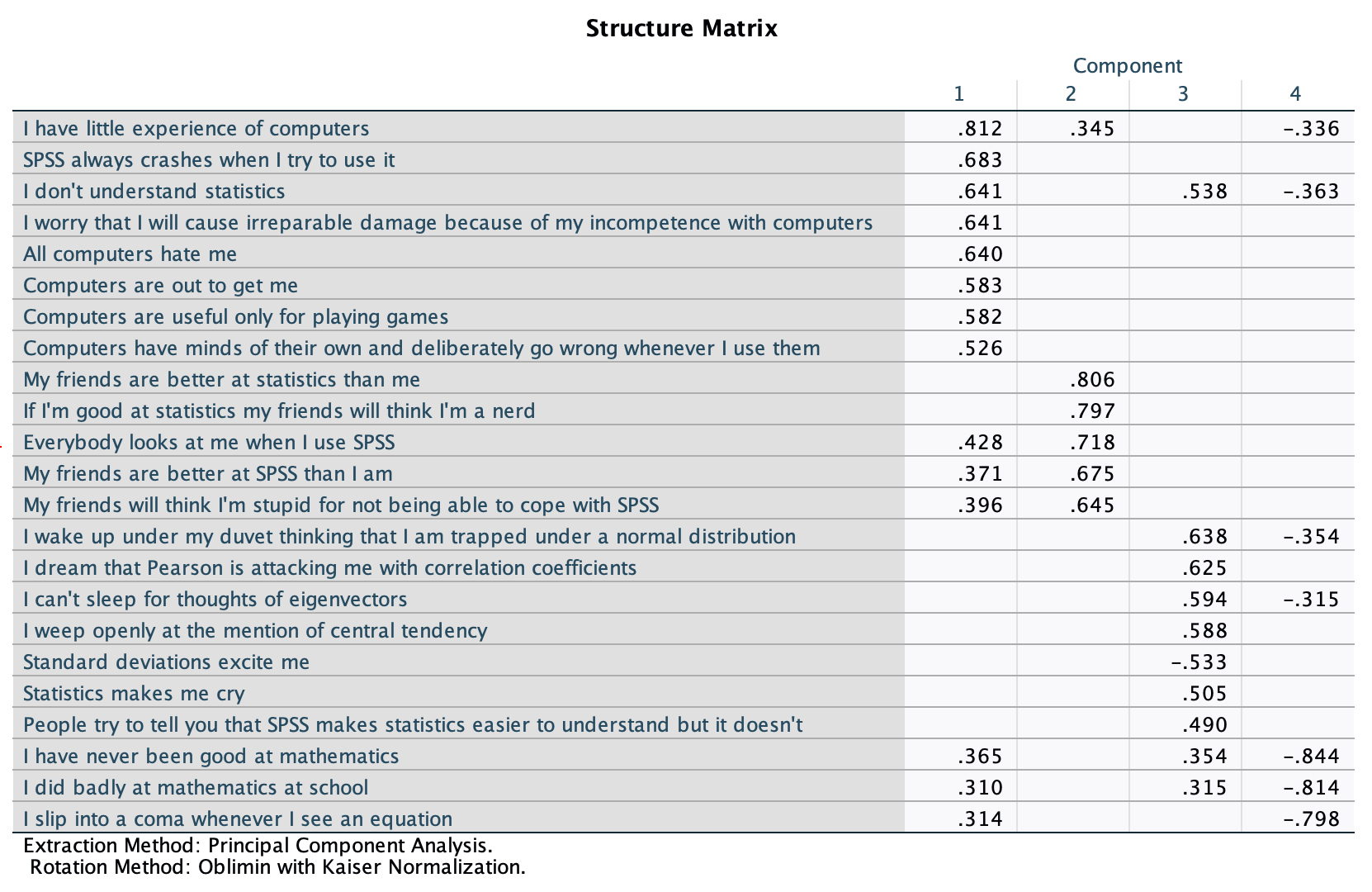
As in the chapter, we can look for themes among questions that load onto the same component. Like the factor analysis in the chapter, the principal components analysis reveals that the initial questionnaire is composed of four subscales:
- Fear of computers: the questions that load highly on component 1 relate to using computers or IBM SPSS Statistics
- Peer evaluation: the questions that load highly on component 2 relate to aspects of peer evaluation
- Fear of statistics: the questions that load highly on component 3 relate to statistics
- Fear of mathematics: the questions that load highly on component 4 relate to mathematics
The component correlation matrix (Figure 403) is comparable to the factor correlation matrix in the book. This matrix contains the correlation coefficients between components. Component 2 has fairly small relationships with all other components (the correlation coefficients are low), but all other components are interrelated to some degree (notably components 1 and 3 and components 3 and 4). The constructs measured appear to be correlated. This dependence between components suggests that oblique rotation was a good decision (that is, the components are not orthogonal/independent).
At a theoretical level the dependence between components makes sense: we might expect a fairly strong relationship between fear of maths, fear of statistics and fear of computers. Generally, the less mathematically and technically minded people struggle with statistics. However, we would not, necessarily, expect these constructs to correlate with fear of peer evaluation (because this construct is more socially based) and this component correlates weakly with the others.
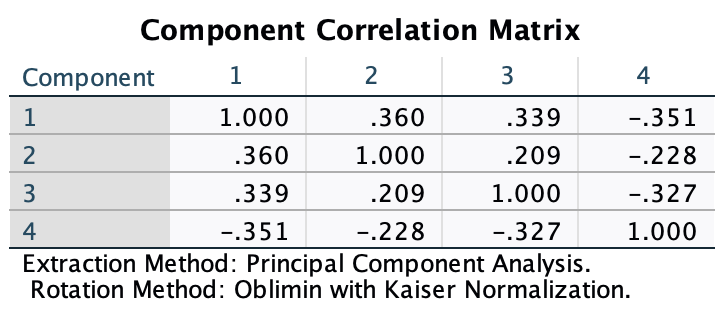
Task 18.2
The University of Sussex constantly seeks to employ the best people possible as lecturers. They wanted to revise the ‘Teaching of Statistics for Scientific Experiments’ (TOSSE) questionnaire, which is based on Bland’s theory which says that good research methods lecturers should have: (1) a profound love of statistics; (2) an enthusiasm for experimental design; (3) a love of teaching; and (4) a complete absence of normal interpersonal skills. These characteristics should be related (i.e., correlated). The University revised this questionnaire to become the ‘Teaching of Statistics for Scientific Experiments – Revised’ (TOSSE–R; Figure 18.18). They gave this questionnaire to 239 research methods lecturers to see if it supported Bland’s theory. Conduct a factor analysis (with appropriate rotation) and interpret the factor structure (
tosser.sav).
Like in the chapter, I ran the analysis with principal axis factoring and oblique rotation. The syntax for my analysis is as follows:
FACTOR
/VARIABLES tosr_01 tosr_02 tosr_03 tosr_04 tosr_05 tosr_06 tosr_07 tosr_08 tosr_09 tosr_10 tosr_11 tosr_12 tosr_13 tosr_14 tosr_15 tosr_16 tosr_17 tosr_18 tosr_19 tosr_20 tosr_21 tosr_22 tosr_23 tosr_24
tosr_25 tosr_26 tosr_27 tosr_28
/MISSING LISTWISE
/ANALYSIS tosr_01 tosr_02 tosr_03 tosr_04 tosr_05 tosr_06 tosr_07 tosr_08 tosr_09 tosr_10 tosr_11 tosr_12 tosr_13 tosr_14 tosr_15 tosr_16 tosr_17 tosr_18 tosr_19 tosr_20 tosr_21 tosr_22 tosr_23 tosr_24
tosr_25 tosr_26 tosr_27 tosr_28
/PRINT UNIVARIATE INITIAL CORRELATION SIG DET KMO INV REPR AIC EXTRACTION ROTATION
/FORMAT SORT BLANK(.30)
/PLOT EIGEN
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PAF
/CRITERIA ITERATE(25) DELTA(0)
/ROTATION OBLIMIN
/METHOD=CORRELATION.Multicollinearity: The determinant of the correlation matrix was 1.240E-6 (i.e., 0.00000124), which is smaller than 0.00001 and, therefore, indicates that multicollinearity could be a problem in these data (Figure 404).

Sample size: MacCallum et al. (1999) have demonstrated that when communalities after extraction are above 0.5 a sample size between 100 and 200 can be adequate, and even when communalities are below 0.5 a sample size of 500 should be sufficient. We have a sample size of 239 with some communalities below 0.5, and so the sample size may not be adequate.
Are the variables adequate?: The KMO measure of sampling adequacy is .894, which is above Kaiser’s (1974) recommendation of 0.5. This value is also ‘meritorious’ (and almost ‘marvellous’). As such, the evidence suggests that the date are adequate to yield distinct and reliable factors.
Bartlett’s test (Figure 405): This tests whether the correlations between questions are sufficiently large for factor analysis to be appropriate (it actually tests whether the correlation matrix is sufficiently different from an identity matrix). In this case it is significant, \(\chi^2\)(378) = 5075.02, p < .001, indicating that the correlations within the R-matrix are sufficiently different from zero. Not surprising given the sample size.

Extraction: By default five factors are extracted based on Kaiser’s criterion of retaining factors with eigenvalues greater than 1 (Figure 406). Is this warranted? Kaiser’s criterion is accurate when there are fewer than 30 variables and the communalities (Figure 407) after extraction are greater than 0.7, or when the sample size exceeds 250 and the average communality is greater than 0.6. For these data the sample size is 239, there are 28 variables, and the mean communality is 10.111/28 = 0.36, so extracting five factors is not really warranted. The scree plot (Figure 408) shows a clear inflexion at 5 factors and so using the scree plot you could justify extracting 4 factors.
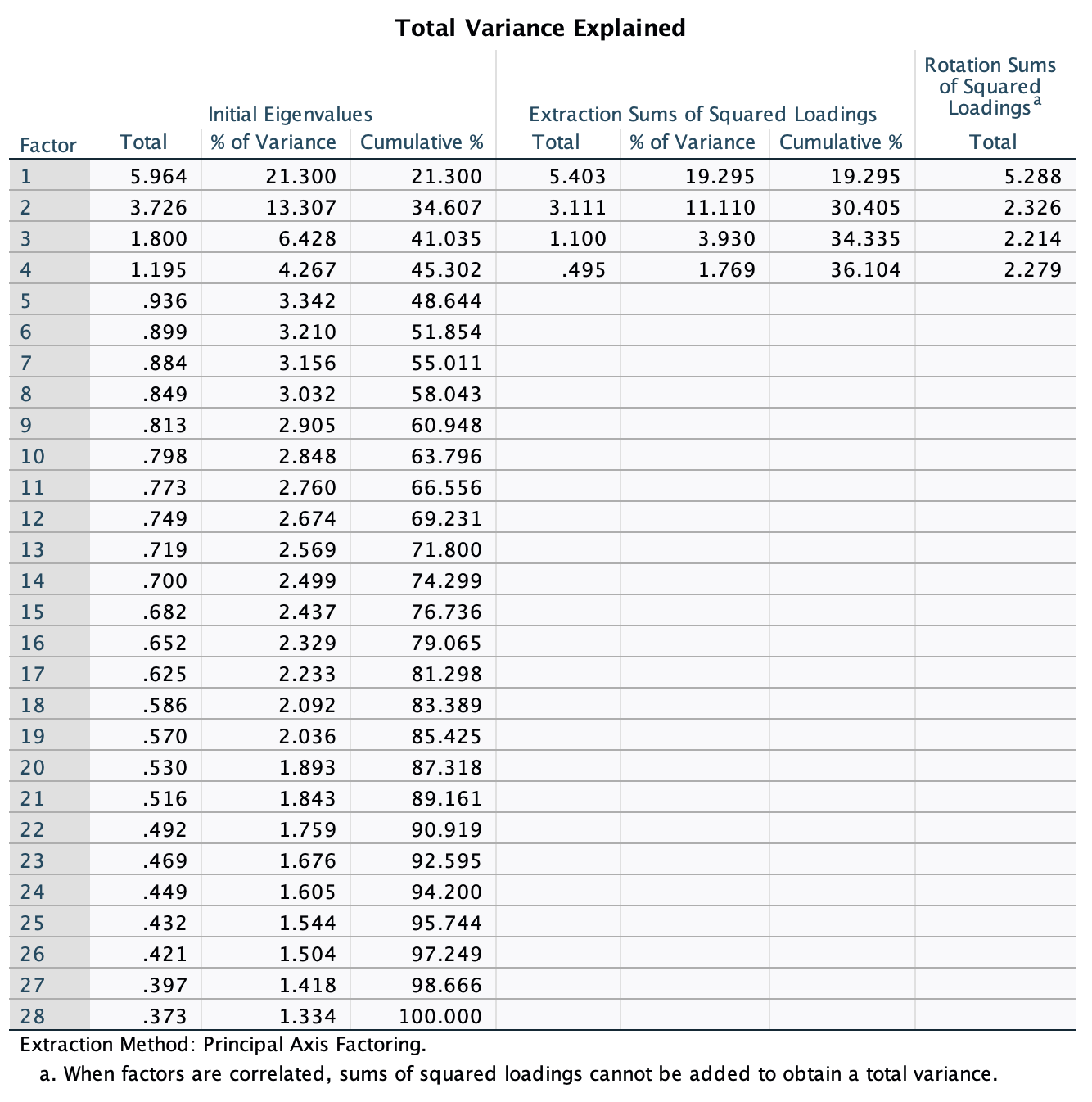
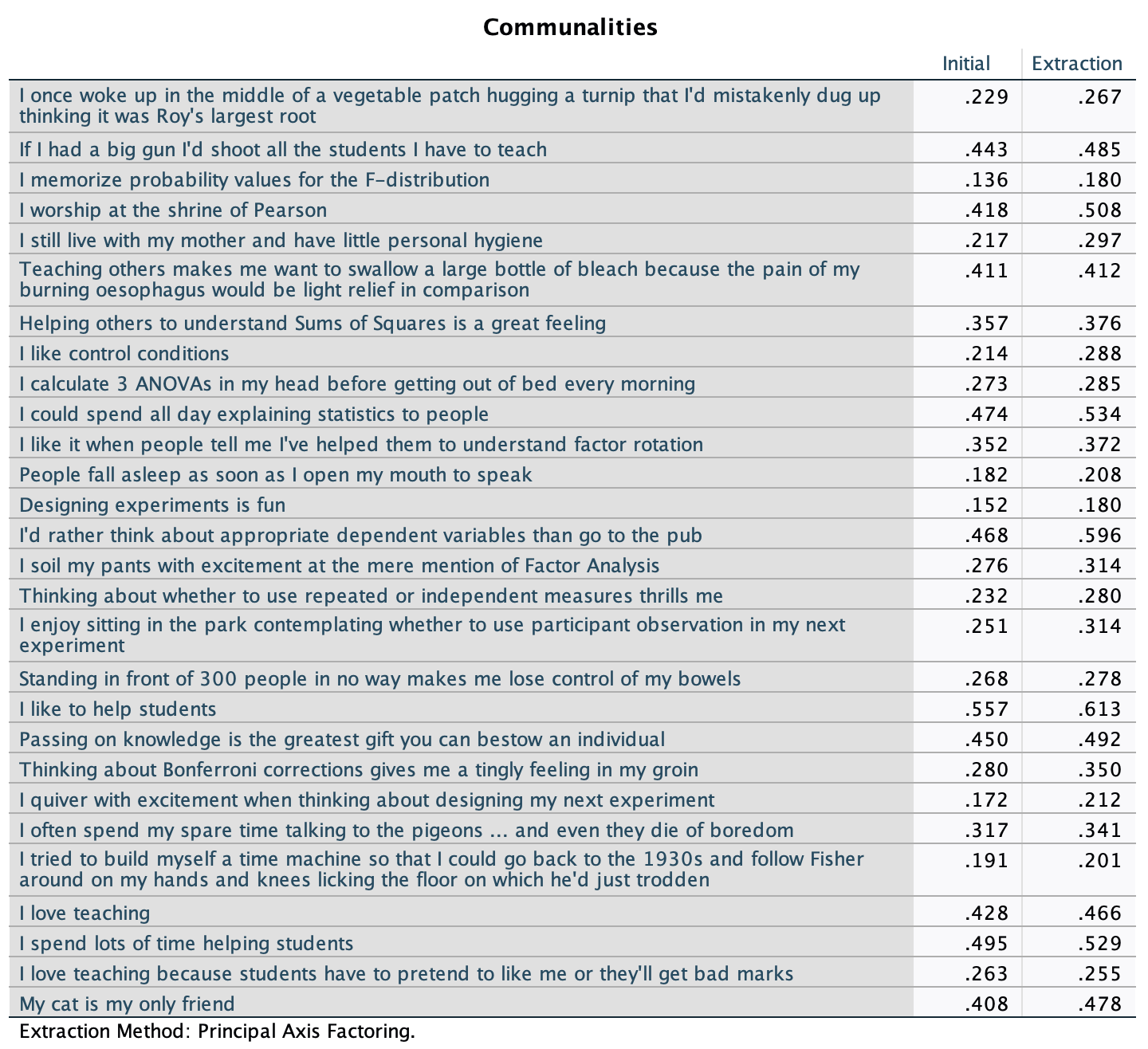
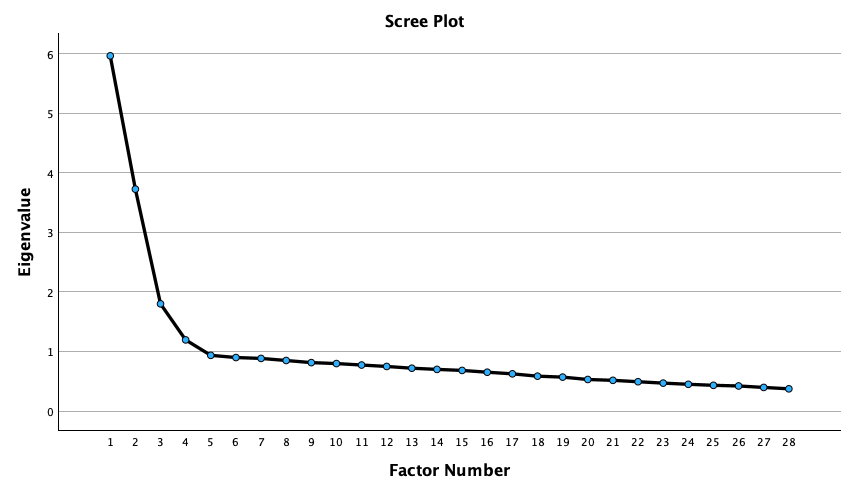
Rotation: You should choose an oblique rotation because the question says that the constructs we’re measuring are related.
Looking at the pattern matrix (Figure 409) and using loadings greater than 0.3 as recommended by Stevens) we see the following (note negative loadings for reversed items):
Factor 1 (Love of teaching)
- I like to help students
- If I had a big gun I’d shoot all the students I have to teach
- I spend lots of time helping students
- Passing on knowledge is the greatest gift you can bestow an individual
- I could spend all day explaining statistics to people
- I love teaching
- Teaching others makes me want to swallow a large bottle of bleach because the pain of my burning oesophagus would be light relief in comparison
- Helping others to understand Sums of Squares is a great feeling
- I like it when people tell me I’ve helped them to understand factor rotation
- I love teaching because students have to pretend to like me or they’ll get bad marks
- Standing in front of 300 people in no way makes me lose control of my bowels
Factor 2 (Love of Statistics)
- Thinking about Bonferroni corrections gives me a tingly feeling in my groin
- I worship at the shrine of Pearson
- I once woke up in the middle of a vegetable patch hugging a turnip that I’d mistakenly dug up thinking it was Roy’s largest root
- I memorize probability values for the F-distribution
- I tried to build myself a time machine so that I could go back to the 1930s and follow Fisher around on my hands and knees licking the floor on which he’d just trodden
- I soil my pants with excitement at the mere mention of Factor Analysis
- I calculate 3 ANOVAs in my head before getting out of bed every morning
Factor 3 (Love of research design)
- I’d rather think about appropriate dependent variables than go to the pub
- I enjoy sitting in the park contemplating whether to use participant observation in my next experiment
- Thinking about whether to use repeated or independent measures thrills me
- I like control conditions
- I quiver with excitement when thinking about designing my next experiment
- Designing experiments is fun
Factor 4 (Interpersonal skills)
- I still live with my mother and have little personal hygiene
- My cat is my only friend
- I often spend my spare time talking to the pigeons … and even they die of boredom
- People fall asleep as soon as I open my mouth to speak
This factor structure supports the original four-factor model.
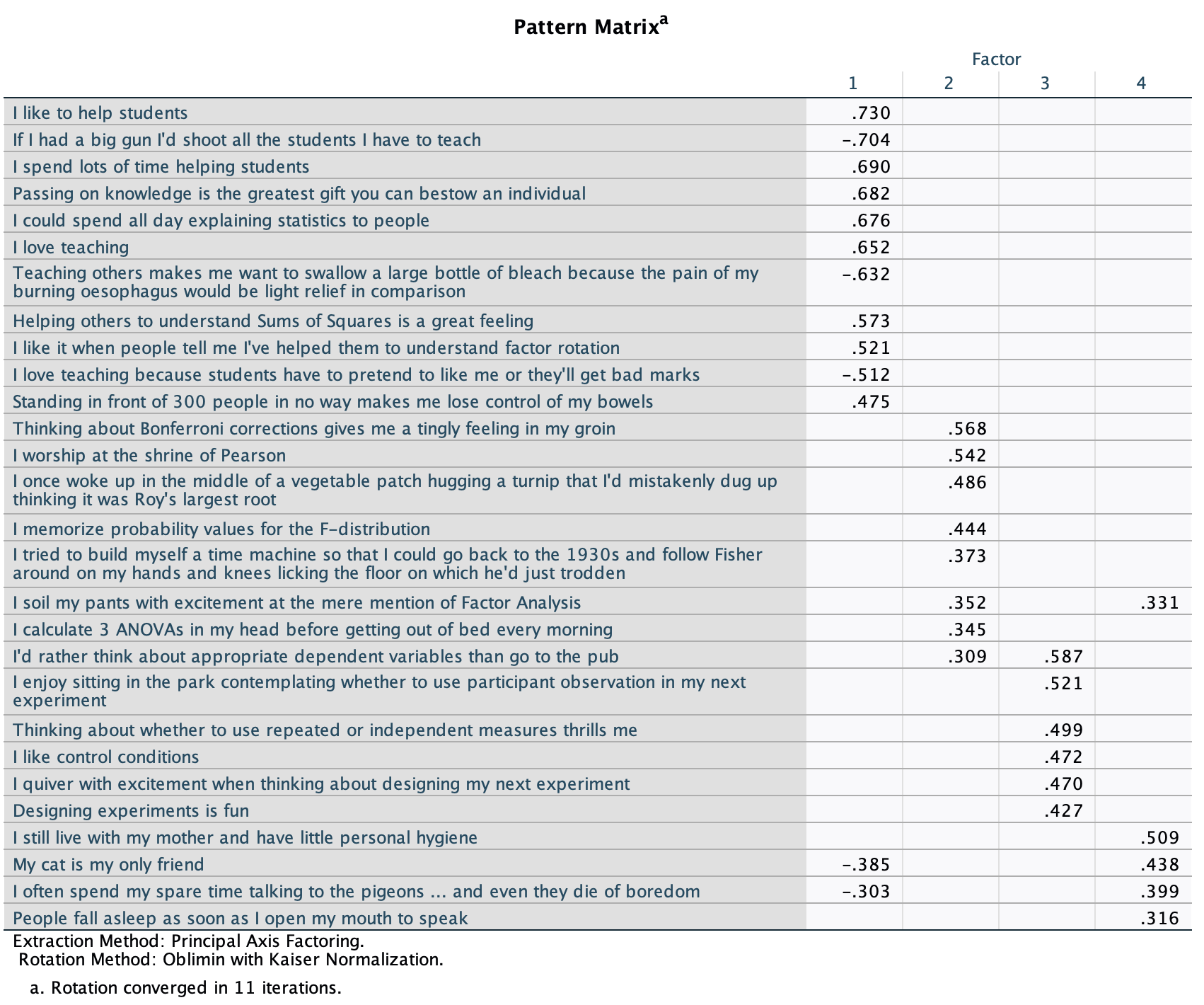
Task 18.3
Dr Sian Williams (University of Brighton) devised a questionnaire to measure organizational ability. She predicted five factors to do with organizational ability: (1) preference for organization; (2) goal achievement; (3) planning approach; (4) acceptance of delays; and (5) preference for routine. These dimensions are theoretically independent. Williams’s questionnaire contains 28 items using a seven-point Likert scale (1 = strongly disagree, 4 = neither, 7 = strongly agree). She gave it to 239 people. Run a principal component analysis on the data in
williams.sav.
The questionnaire items are as follows:
- I like to have a plan to work to in everyday life
- I feel frustrated when things don’t go to plan
- I get most things done in a day that I want to
- I stick to a plan once I have made it
- I enjoy spontaneity and uncertainty
- I feel frustrated if I can’t find something I need
- I find it difficult to follow a plan through
- I am an organized person
- I like to know what I have to do in a day
- Disorganized people annoy me
- I leave things to the last minute
- I have many different plans relating to the same goal
- I like to have my documents filed and in order
- I find it easy to work in a disorganized environment
- I make ‘to do’ lists and achieve most of the things on it
- My workspace is messy and disorganized
- I like to be organized
- Interruptions to my daily routine annoy me
- I feel that I am wasting my time
- I forget the plans I have made
- I prioritize the things I have to do
- I like to work in an organized environment
- I feel relaxed when I don’t have a routine
- I set deadlines for myself and achieve them
- I change rather aimlessly from one activity to another during the day
- I have trouble organizing the things I have to do
- I put tasks off to another day
- I feel restricted by schedules and plans
I ran the analysis with principal components and oblique rotation. The syntax for my analysis is as follows:
FACTOR
/VARIABLES org_01 org_02 org_03 org_04 org_06 org_07 org_09 org_10 org_11 org_12 org_13 org_14 org_16 org_17 org_18 org_19 org_20 org_21 org_22 org_23 org_24 org_25 org_26 org_27 org_28
/MISSING LISTWISE
/ANALYSIS org_01 org_02 org_03 org_04 org_06 org_07 org_09 org_10 org_11 org_12 org_13 org_14 org_16 org_17 org_18 org_19 org_20 org_21 org_22 org_23 org_24 org_25 org_26 org_27 org_28
/PRINT UNIVARIATE INITIAL CORRELATION SIG DET KMO INV REPR AIC EXTRACTION ROTATION
/FORMAT SORT BLANK(.30)
/PLOT EIGEN
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/CRITERIA ITERATE(25) DELTA(0)
/ROTATION OBLIMIN
/METHOD=CORRELATION.The outputs are shown in Figure 410 to Figure 413. By default, five components have been extracted based on Kaiser’s criterion. The scree plot shows clear inflexions at 3 and 5 factors, and so using the scree plot you could justify extracting 3 or 5 factors.
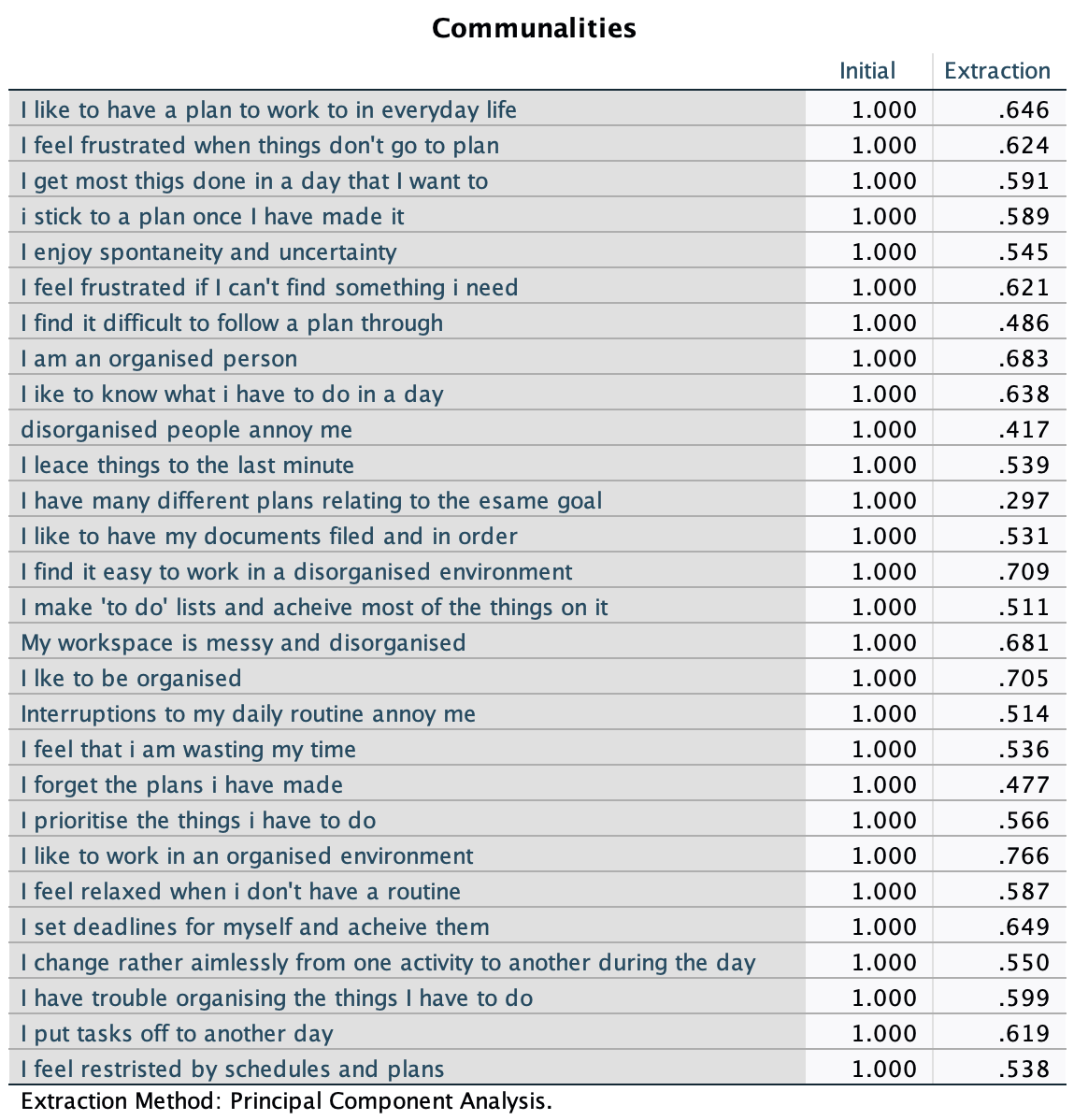
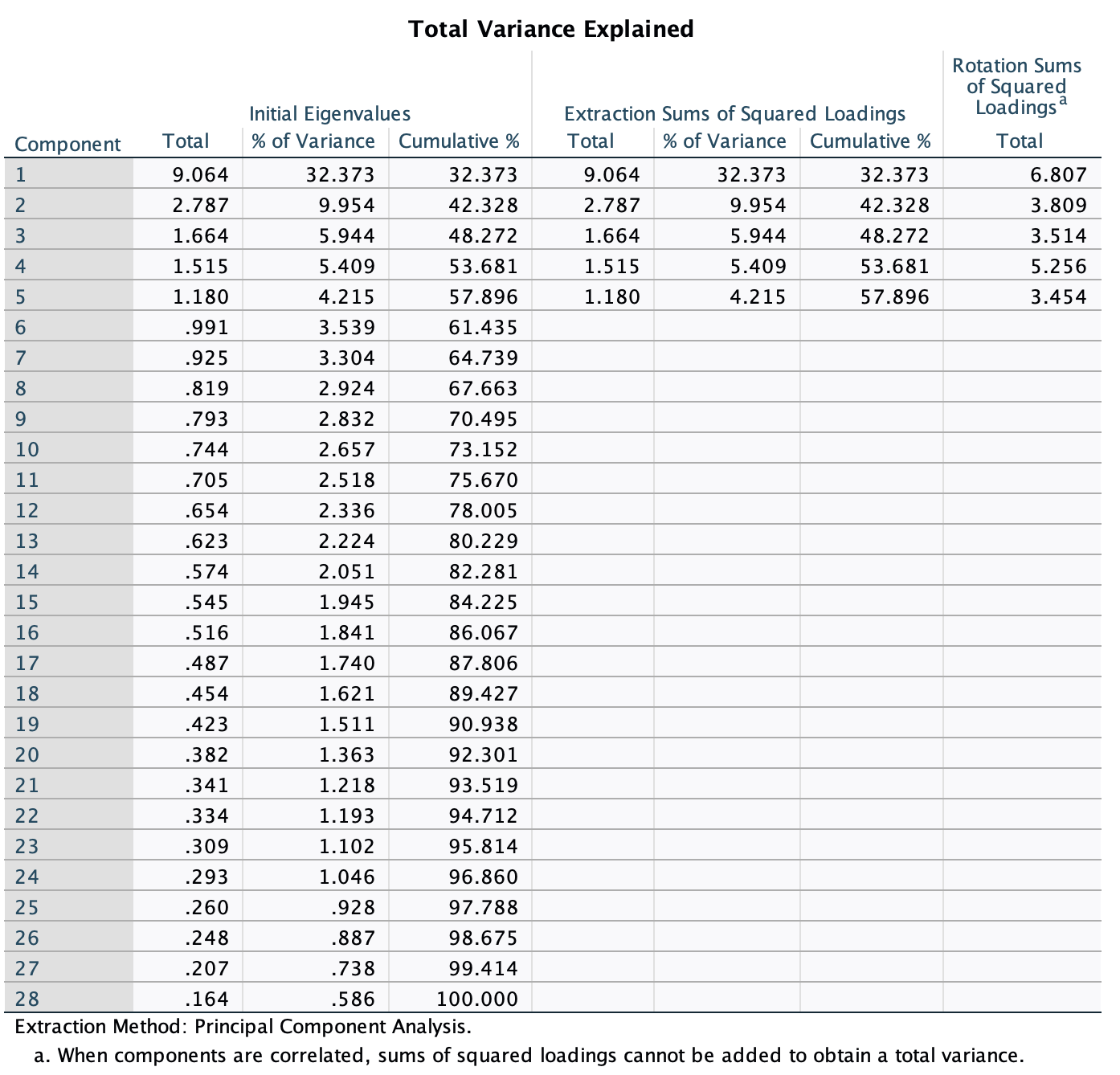
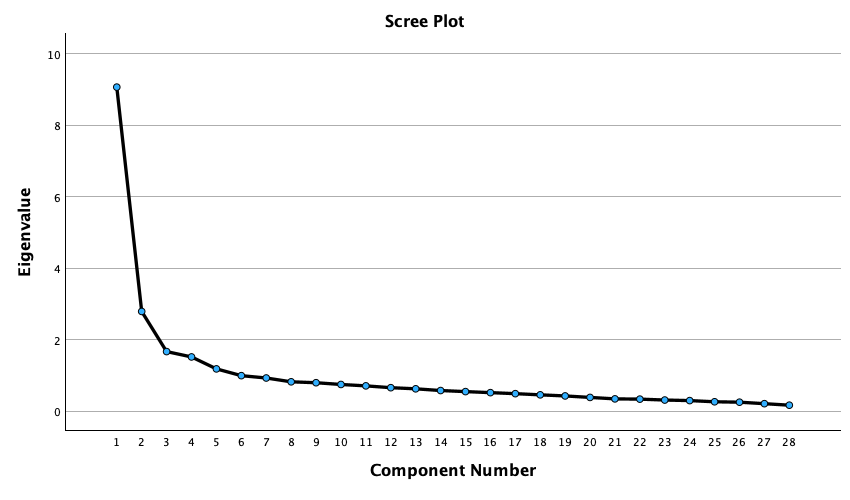
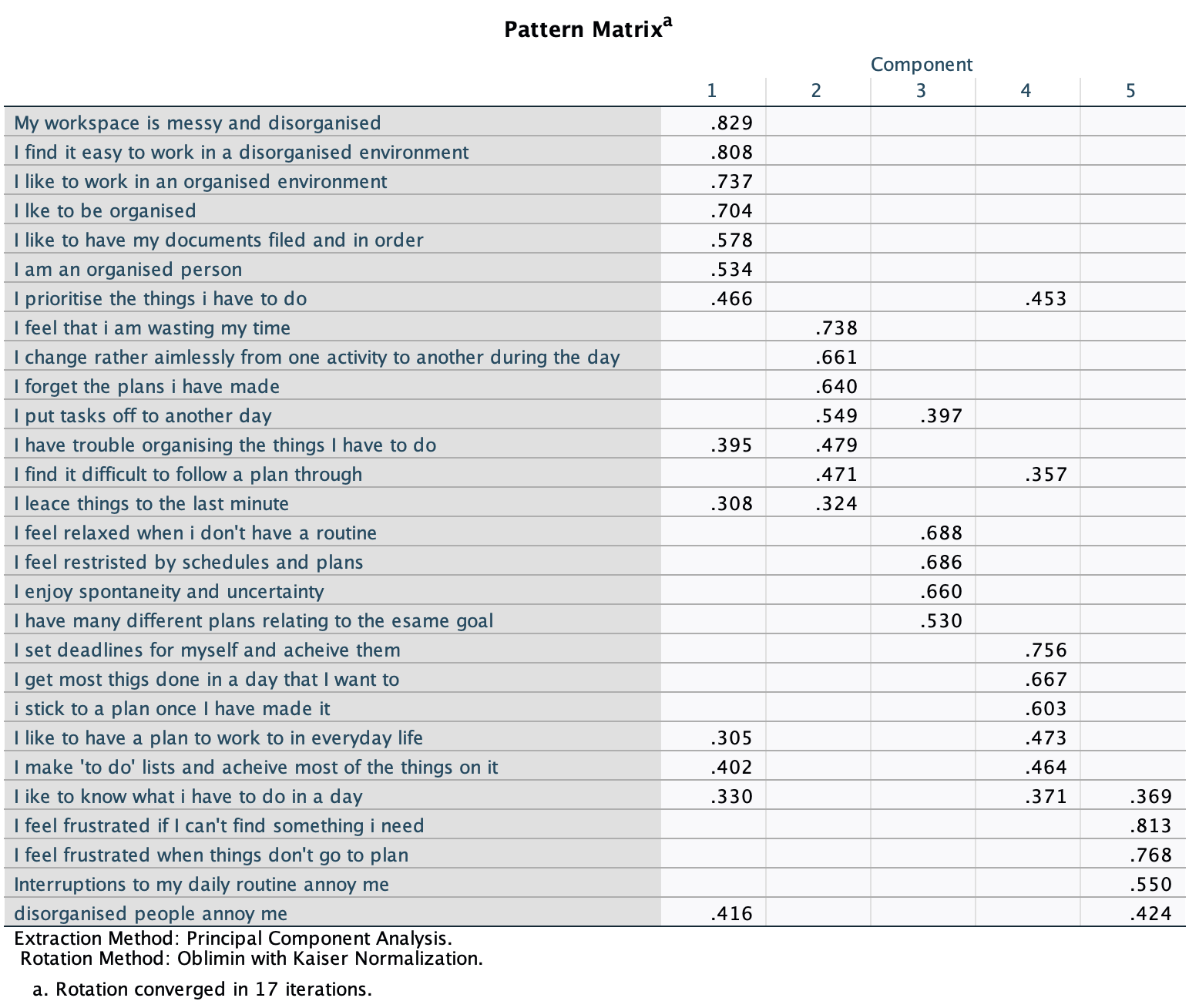
Looking at the rotated component matrix (and using loadings greater than 0.4) we see the following pattern:
Component 1: preference for organization
Note: It’s odd that none of these have reverse loadings.
- Q8: I am an organized person
- Q13: I like to have my documents filed and in order
- Q14: I find it easy to work in a disorganized environment
- Q16: My workspace is messy and disorganized
- Q17: I like to be organized
- Q22: I like to work in an organized environment
Component 2: goal achievement
- Q7: I find it difficult to follow a plan through
- Q11: I leave things to the last minute
- Q19: I feel that I am wasting my time
- Q20: I forget the plans I have made
- Q25: I change rather aimlessly from one activity to another during the day
- Q26: I have trouble organizing the things I have to do
- Q27: I put tasks off to another day
Component 3: preference for routine
- Q5: I enjoy spontaneity and uncertainty
- Q12: I have many different plans relating to the same goal
- Q23: I feel relaxed when I don’t have a routine
- Q28: I feel restricted by schedules and plans
Component 4: plan approach
- Q1: I like to have a plan to work to in everyday life
- Q3: I get most things done in a day that I want to
- Q4: I stick to a plan once I have made it
- Q9: I like to know what I have to do in a day
- Q15: I make ‘to do’ lists and achieve most of the things on it
- Q 21: I prioritize the things I have to do
- Q24: I set deadlines for myself and achieve them
Component 5: acceptance of delays
- Q2: I feel frustrated when things don’t go to plan
- Q6: I feel frustrated if I can’t find something I need
- Q10: Disorganized people annoy me
- Q18: Interruptions to my daily routine annoy me
It seems as though there is some factorial validity to the structure.
Task 18.4
Zibarras et al. (2008) looked at the relationship between personality and creativity. They used the Hogan Development Survey (HDS), which measures 11 dysfunctional dispositions of employed adults: being
volatile,mistrustful,cautious,detached,passive_aggressive,arrogant,manipulative,dramatic,eccentric,perfectionist, anddependent.Zibarras et al. wanted to reduce these 11 traits down and, based on parallel analysis, found that they could be reduced to three components. They ran a principal component analysis with varimax rotation. Repeat this analysis (zibarras_2008.sav) to see which personality dimensions clustered together (see page 210 of the original paper). .
As indicated in the question, I ran the analysis with principal components and varimax rotation. I specified to extract three factors to match Zibarras et al. (2008). The syntax for my analysis is as follows:
FACTOR
/VARIABLES volatile mistrustful cautious detached passive_aggressive arrogant manipulative
dramatic eccentric perfectist dependent
/MISSING LISTWISE
/ANALYSIS volatile mistrustful cautious detached passive_aggressive arrogant manipulative
dramatic eccentric perfectist dependent
/PRINT UNIVARIATE INITIAL CORRELATION SIG DET KMO INV REPR AIC EXTRACTION ROTATION
/FORMAT SORT BLANK(.30)
/PLOT EIGEN
/CRITERIA FACTORS(3) ITERATE(25)
/EXTRACTION PC
/CRITERIA ITERATE(25)
/ROTATION VARIMAX
/METHOD=CORRELATION.The output (Figure 414) shows the rotated component matrix, from which we see this pattern:
- Component 1:
- Dramatic
- Manipulative
- Arrogant
- Cautious (negative weight)
- Eccentric
- Perfectionist (negative weight)
- Component 2:
- Volatile
- Mistrustful
- Component 3:
- Detached
- Dependent (negative weight)
- Passive-aggressive
Compare these results to those of Zibarras et al. (Table 4 from the original paper reproduced in Figure 415), and note that they are the same.
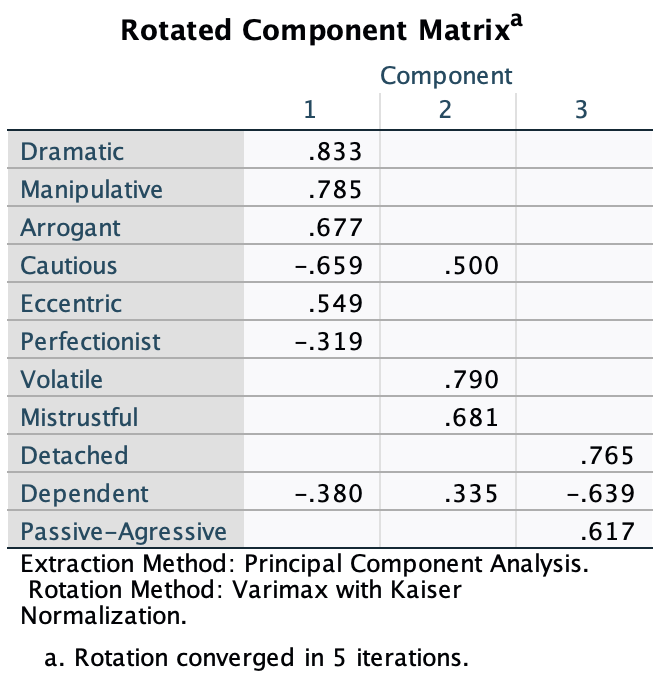
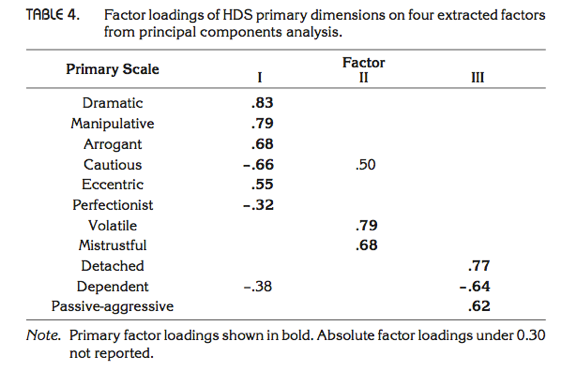
Chapter 19
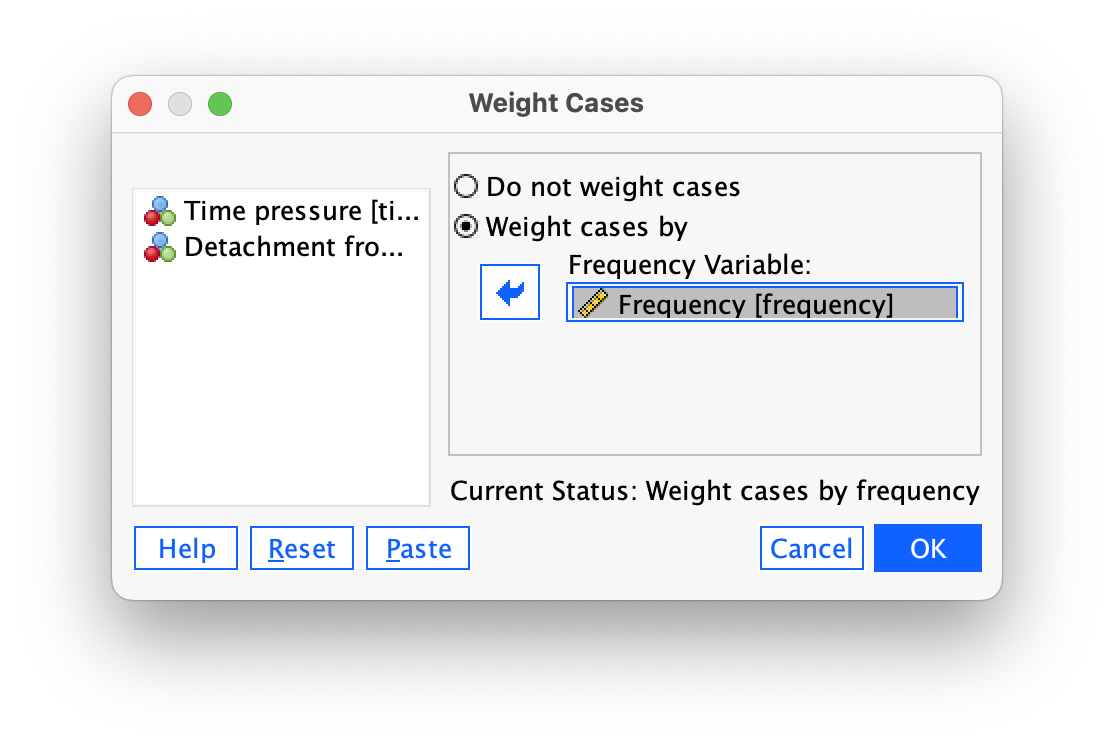
Task 19.1
Research suggests that people who can switch off from work (
detachment) during off-hours are more satisfied with life and have fewer symptoms of psychological strain (Sonnentag, 2012). Factors at work, such as time pressure, affect your ability to detach when away from work. A study of 1709 employees measured their time pressure (time_pressure) at work (no time pressure, low, medium, high and very high time pressure). Data generated to approximate Figure 1 in Sonnentag (2012) are in the filesonnentag_2012.sav. Carry out a chi-square test to see if time pressure is associated with the ability to detach from work.
Follow the general procedure for this chapter. First, weight cases by the variable frequency (see Figure 416). To conduct the chi-square test, use the crosstabs command by selecting Analyze > Descriptive Statistics > Crosstabs …. We have two variables in our crosstabulation table: detachment and time_pressure. Drag one of these variables into the box labelled Row(s) (I selected time_pressure in the figure). Next, drag the other variable of interest (detachment) to the box labelled Column(s) (Figure 420). Use the book chapter to select other appropriate options.
The chi-square test is highly significant, \(\chi^2\) 2(4) = 15.55, p = .004 (Figure 421), indicating that the profile of low-detachment and very low-detachment responses differed significantly across different time pressures. Looking at the standardized residuals (Figure 422), the only time pressure for which these are significant is very high time pressure, which showed the greatest split of whether the employees experienced low detachment (36%) or very low detachment (64%). Within the other time pressure groups all of the standardized residuals are lower than 1.96. It’s interesting to look at the direction of the residuals (i.e., whether they are positive or negative). For all time pressure groups except very high time pressure, the residual for ‘low detachment’ was positive but for ‘very low detachment’ was negative; these are, therefore, people who responded more than we would expect that they experienced low detachment from work and less than expected that they experienced very low detachment from work. It was only under very high time pressure that the opposite pattern occurred: the residual for ‘low detachment’ was negative but for ‘very low detachment’ was positive; these are, therefore, people who responded less than we would expect that they experienced low detachment from work and more than expected that they experienced very low detachment from work. In short, there are similar numbers of people who experience low detachment and very low detachment from work when there is no time pressure, low time pressure, medium time pressure and high time pressure. However, when time pressure was very high, significantly more people experienced very low detachment than low detachment.
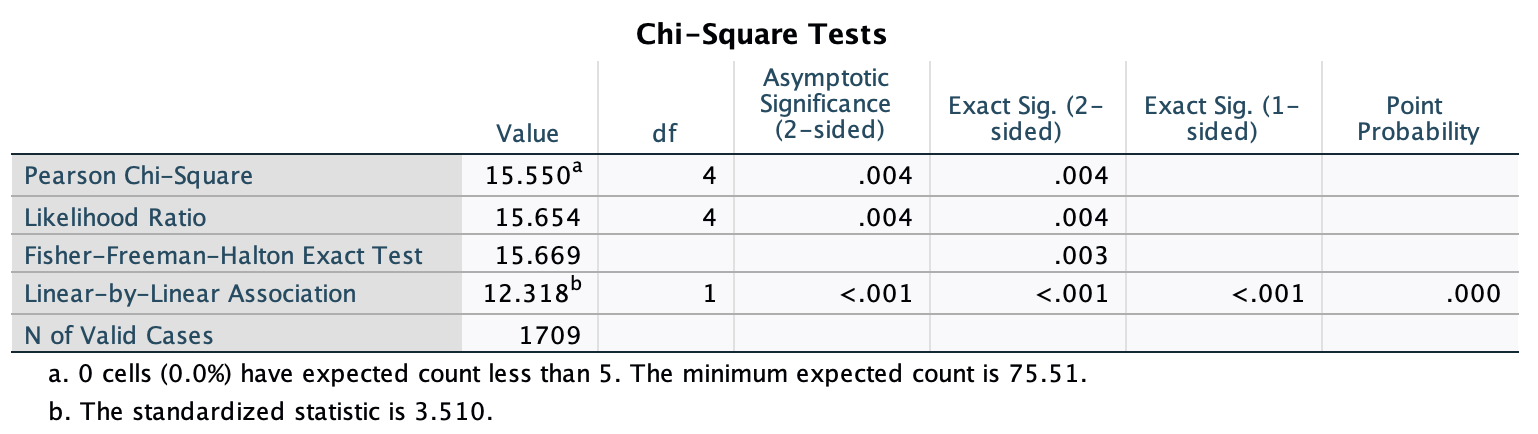
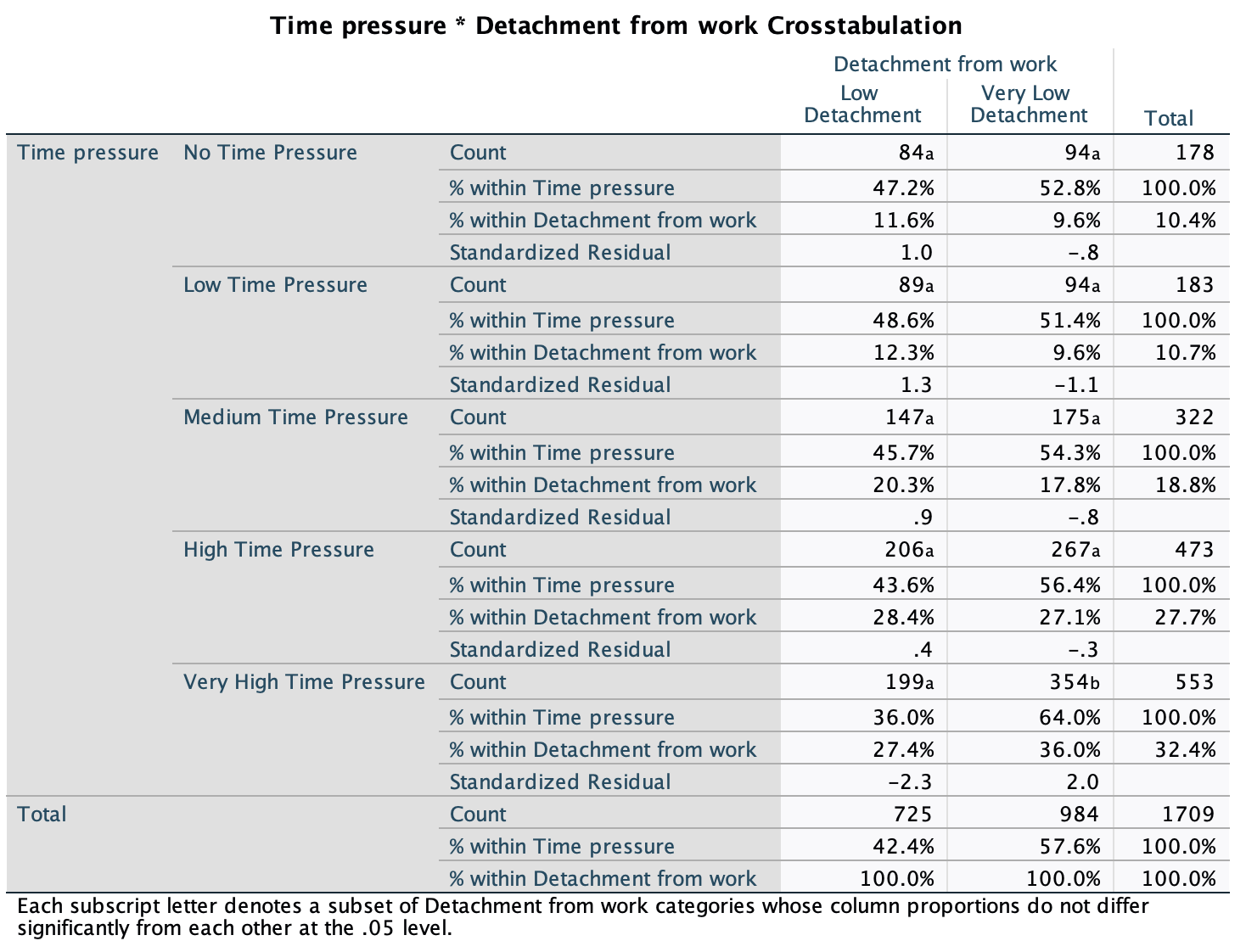
Task 19.2
Labcoat Leni’s Real Research 19.1 describes a study (Daniels, 2012) that looked at the impact of sexualized images of atheletes compared to performance pictures on women’s perceptions of the athletes and of themselves. Women looked at different types of pictures (
picture) and then did a writing task. Daniels identified whether certain themes were present or absent in each written piece (theme_present). We looked at the self-evaluation theme, but Daniels idetified others: commenting on the athlete’s body/appearance (athletes_body), indicating admiration or jelousy for the athlete (admiration), indicating that the athlete was a role model or motivating (role_model), and their own physical activity (self_physical_activity). Test whether the type of picture viewed was associated with commenting on the athlete’s body/appearance (daniels_2012.sav).
Follow the general procedure for this chapter. First, weight cases by the variable athletes_body. Next, access the crosstabs command by selecting Analyze > Descriptive Statistics > Crosstabs …. We have two variables in our crosstabulation table: picture and theme_present. Drag one of these variables into the box labelled Row(s) (I selected picture in the figure). Next, drag the other variable of interest (theme_present) to the box labelled Column(s) (Figure 423). Select the options indicated in the general procedure.
The chi-square test is highly significant, \(\chi^2\)(1) = 104.92, p < .001 (Figure 424). This indicates that the profile of theme present vs. theme absent differed across different pictures.
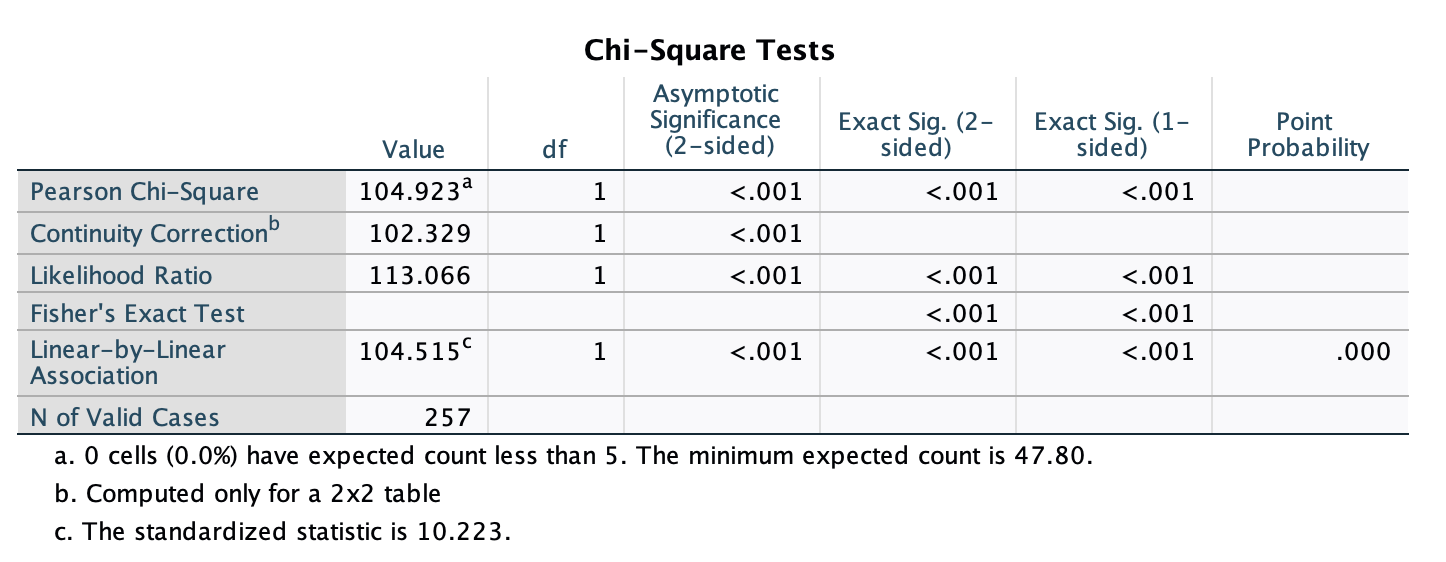
Looking at the standardized residuals (Figure 425), they are significant for both pictures of performance athletes and sexualized pictures of athletes. If we look at the direction of these residuals (i.e., whether they are positive or negative), we can see that for pictures of performance athletes, the residual for ‘theme absent’ was positive but for ‘theme present’ was negative; this indicates that in this condition, more people than we would expect did not include the theme her appearance and attractiveness and fewer people than we would expect did include this theme in what they wrote. In the sexualized picture condition on the other hand, the opposite was true: the residual for ‘theme absent’ was negative and for ‘theme present’ was positive. This indicates that in the sexualized picture condition, more people than we would expect included the theme her appearance and attractiveness in what they wrote and fewer people than we would expect did not include this theme in what they wrote.
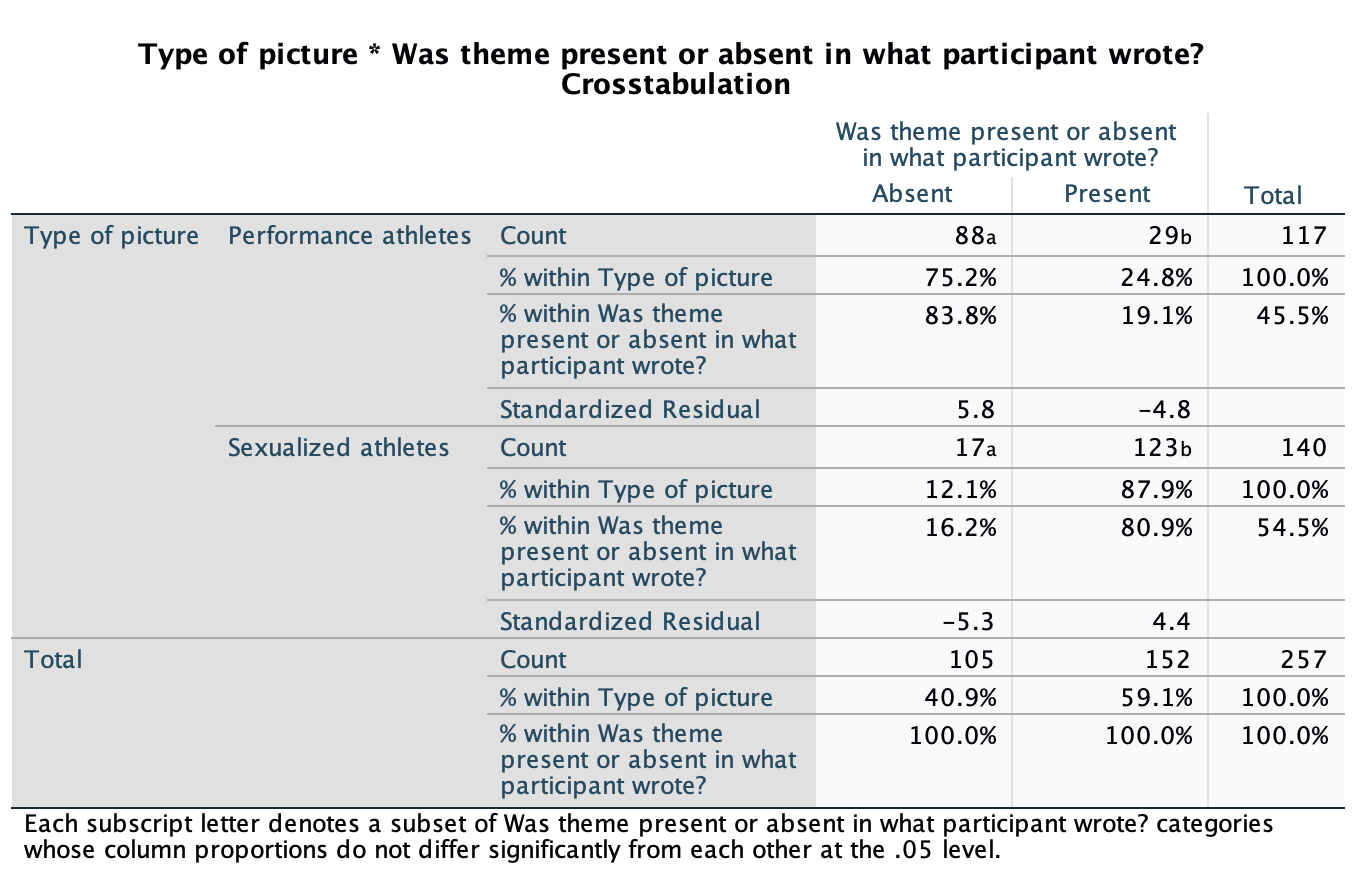
Task 19.3
Using the data in Task 2, see whether the type of picture viewed was associated with indicating admiration or jelousy for the athlete.
Follow the general procedure for this chapter. First, weight cases by the variable admiration. Next, access the crosstabs command by selecting Analyze > Descriptive Statistics > Crosstabs …. We have two variables in our crosstabulation table: picture and theme_present. Drag one of these variables into the box labelled Row(s) (I selected picture in the figure). Next, drag the other variable of interest (theme_present) to the box labelled Column(s) (Figure 423). Select the options indicated in the general procedure.
The chi-square test is highly significant, \(\chi^2\)(1) = 28.98, p < .001 (Figure 427). This indicates that the profile of theme present vs. theme absent differed across different pictures.
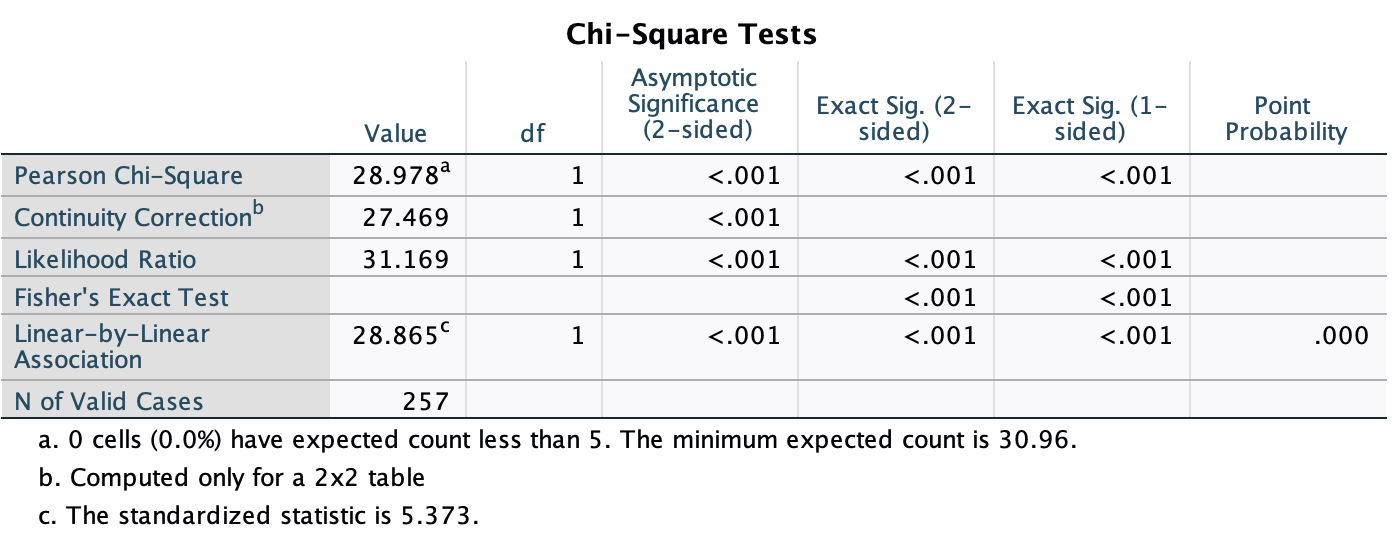
Looking at the standardized residuals (Figure 428), they are significant for both pictures of performance athletes and sexualized pictures of athletes. If we look at the direction of these residuals (i.e., whether they are positive or negative), we can see that for pictures of performance athletes, the residual for ‘theme absent’ was positive but for ‘theme present’ was negative; this indicates that in this condition, more people than we would expect did not include the theme My admiration or jealousy for the athlete and fewer people than we would expect did include this theme in what they wrote. In the sexualized picture condition, on the other hand, the opposite was true: the residual for ‘theme absent’ was negative and for ‘theme present was positive’. This indicates that in the sexualized picture condition, more people than we would expect included the theme My admiration or jealousy for the athlete in what they wrote and fewer people than we would expect did not include this theme in what they wrote.

Task 19.4
Using the data in Task 2, see whether the type of picture viewed was associated with indicating that the athlete was a role model or motivating.
Follow the general procedure for this chapter. First, weight cases by the variable role_model. Next, access the crosstabs command by selecting Analyze > Descriptive Statistics > Crosstabs …. We have two variables in our crosstabulation table: picture and theme_present. Drag one of these variables into the box labelled Row(s) (I selected picture in the figure). Next, drag the other variable of interest (theme_present) to the box labelled Column(s) (Figure 423). Select the options indicated in the general procedure.
The chi-square test is highly significant, \(\chi^2\)(1) = 47.50, p < .001 (Figure 430). This indicates that the profile of theme present vs. theme absent differed across different pictures.

Looking at the standardized residuals (Figure 431), they are significant for both types of pictures. If we look at the direction of these residuals (i.e., whether they are positive or negative), we can see that for pictures of performance athletes, the residual for ‘theme absent’ was negative but was positive for ‘theme present’. This indicates that when looking at pictures of performance athletes, more people than we would expect included the theme Athlete is a good role model and fewer people than we would expect did not include this theme in what they wrote. In the sexualized picture condition on the other hand, the opposite was true: the residual for ‘theme absent’ was positive and for ‘theme present’ it was negative. This indicates that in the sexualized picture condition, more people than we would expect did not include the theme Athlete is a good role model in what they wrote and fewer people than we would expect did include this theme in what they wrote.
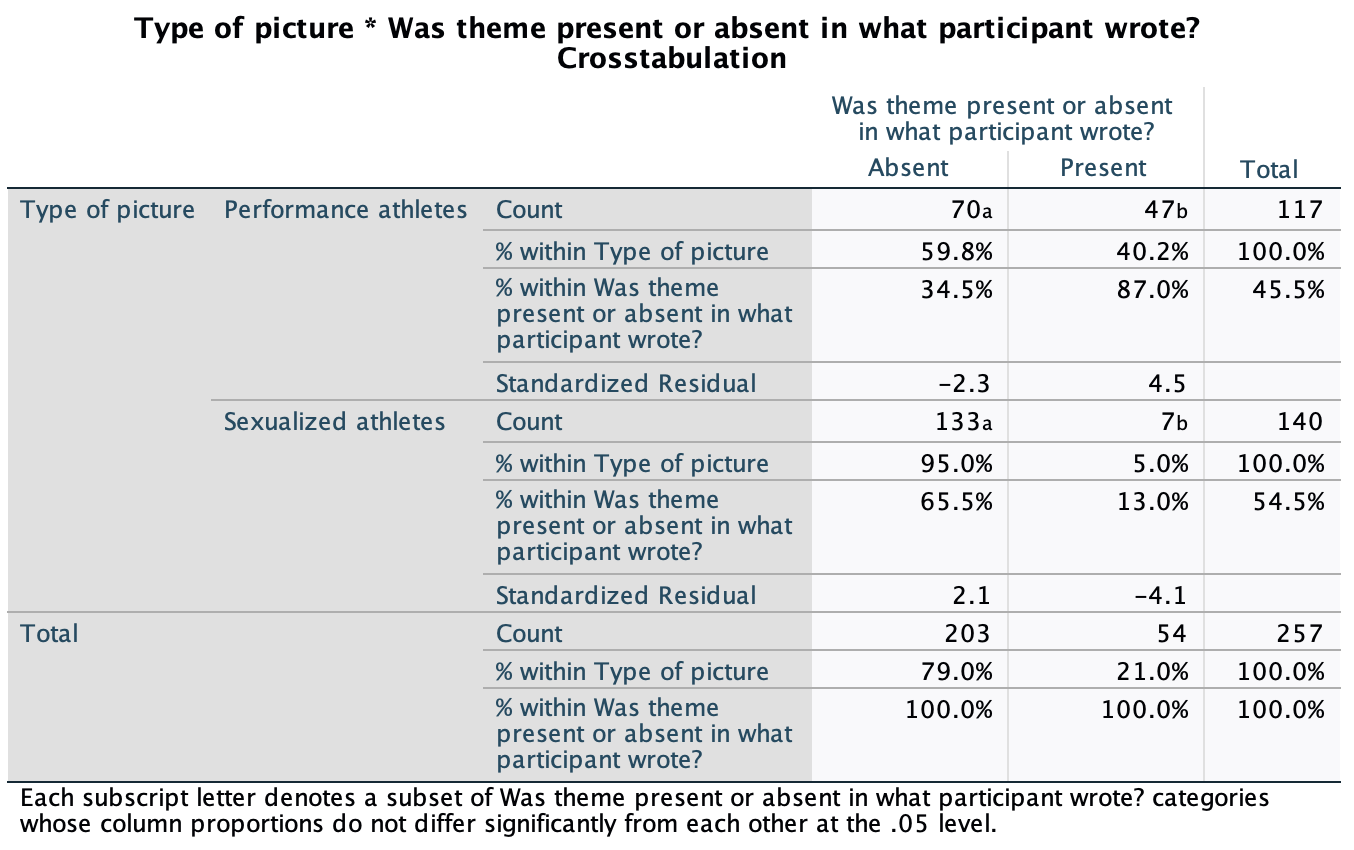
Task 19.5
Using the data in Task 2, see whether the type of picture viewed was associated with the participant commenting on their own physical activity.
Follow the general procedure for this chapter. First, weight cases by the variable self_physical_activity. Next, access the crosstabs command by selecting Analyze > Descriptive Statistics > Crosstabs …. We have two variables in our crosstabulation table: picture and theme_present. Drag one of these variables into the box labelled Row(s) (I selected picture in the figure). Next, drag the other variable of interest (theme_present) to the box labelled Column(s) (Figure 423). Select the options indicated in the general procedure.
The chi-square test is significant, \(\chi^2\)(1) = 5.91, p = .02 (Figure 433). This indicates that the profile of theme present vs. theme absent differed across different pictures.
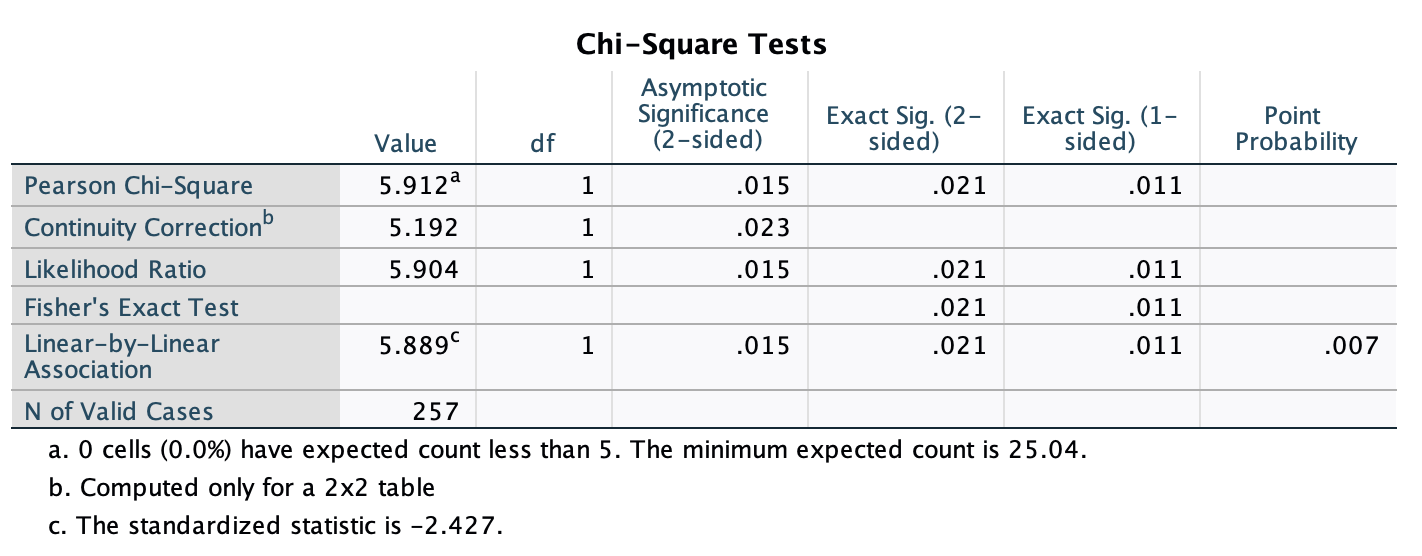
Looking at the standardized residuals (Figure 434), they are not significant for either type of picture (i.e., they are less than 1.96). If we look at the direction of these residuals (i.e., whether they are positive or negative), we can see that for pictures of performance athletes, the residual for ‘theme absent’ was negative and for ‘theme present’ was positive. This indicates that when looking at pictures of performance athletes, more people than we would expect included the theme My own physical activity and fewer people than we would expect did not include this theme in what they wrote. In the sexualized picture condition on the other hand, the opposite was true: the residual for ‘theme absent’ was positive and for ‘theme present’ it was negative. This indicates that in the sexualized picture condition, more people than we would expect did not include the theme My own physical activity in what they wrote and fewer people than we would expect did include this theme in what they wrote.
Task 19.6
I wrote much of the third edition of this book in the Netherlands (I have a soft spot for it). The Dutch travel by bike much more than the English. I noticed that many more Dutch people cycle while steering with only one hand. I pointed this out to one of my friends, Birgit Mayer, and she said that I was a crazy English fool and that Dutch people did not cycle one-handed. Several weeks of me pointing at one-handed cyclists and her pointing at two-handed cyclists ensued. To put it to the test I counted the number of Dutch and English cyclists who ride with one or two hands on the handlebars (
handlebars.sav). Can you work out which one of us is correct?
Follow the general procedure for this chapter. First, weight cases by the variable frequency (Figure 416). We have two variables in our crosstabulation table: nationality and hands. Drag one of these variables into the box labelled Row(s) (I selected nationality in the figure). Next, drag the other variable of interest (hands) to the box labelled Column(s) (Figure 436). Select the options indicated in the general procedure.
The value of the chi-square statistic is 5.44 (Figure 437). This value has a two-tailed significance of .020, which is smaller than .05 (hence significant), which suggests that the pattern of bike riding (i.e., relative numbers of one- and two-handed riders) significantly differs in English and Dutch people. The significant result indicates that there is an association between whether someone is Dutch or English and whether they ride their bike one- or two-handed.
Looking at the frequencies (Figure 438), this significant finding seems to show that the ratio of one- to two-handed riders differs in Dutch and English people. In Dutch people 17.2% ride their bike one-handed compared to 82.8% who ride two-handed. In England, though, only 9.9% ride their bike one-handed (almost half as many as in Holland), and 90.1% ride two-handed. If we look at the standardized residuals (in the contingency table) we can see that the only cell with a residual approaching significance (a value that lies outside of ±1.96) is the cell for English people riding one-handed (z = -1.9). The fact that this value is negative tells us that fewer people than expected fell into this cell.
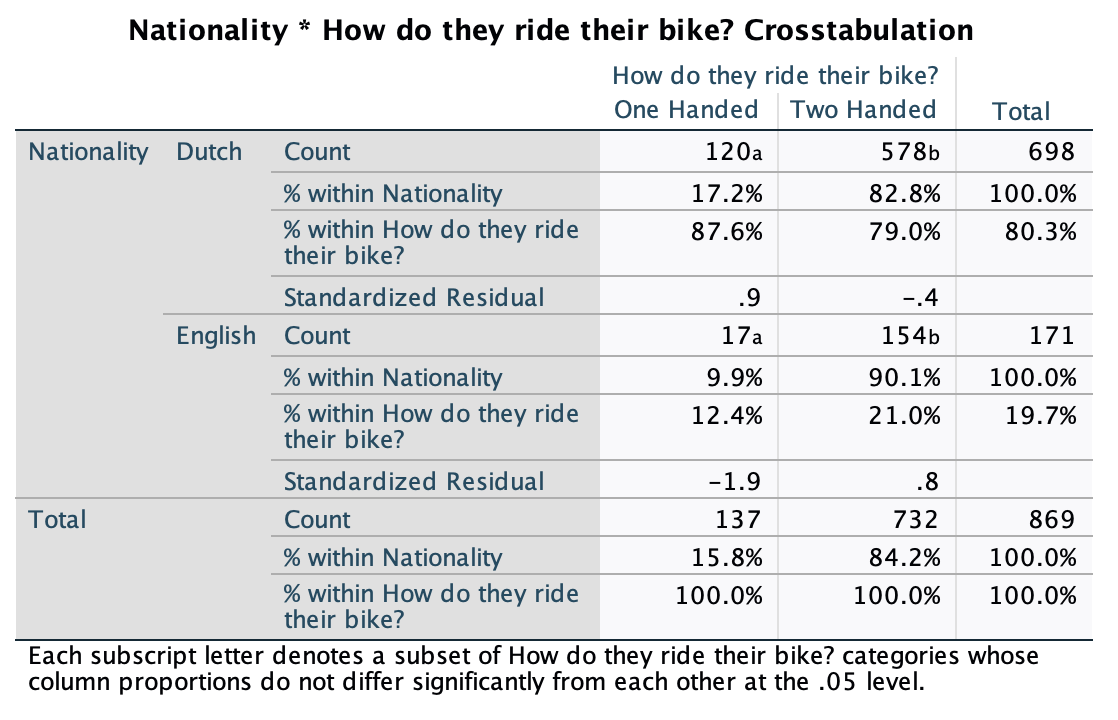
Task 19.7
Compute and interpret the odds ratio for Task 6.
The odds of someone riding one-handed if they are Dutch are:
\[ \text{odds}_\text{one-handed, Dutch} = \frac{120}{578} = 0.21 \]
The odds of someone riding one-handed if they are English are:
\[ \text{odds}_\text{one-handed, English} = \frac{17}{154} = 0.11 \]
Therefore, the odds ratio is:
\[ \text{odds ratio} = \frac{\text{odds}_\text{one-handed, Dutch}}{\text{odds}_\text{one-handed, English}} = \frac{0.21}{0.11} = 1.90 \]
In other words, the odds of riding one-handed if you are Dutch are 1.9 times higher than if you are English (or, conversely, the odds of riding one-handed if you are English are about half that of a Dutch person).
Task 19.8
Certain editors at Sage like to think they’re great at football (soccer). To see whether they are better than Sussex lecturers and postgraduates we invited employees of Sage to join in our football matches. Every person played in one match. Over many matches, we counted the number of players that scored goals. Is there a significant relationship between scoring goals and whether you work for Sage or Sussex? (
sage_editors_can't_play_football.sav)
Follow the general procedure for this chapter. First, weight cases by the variable frequency. We have two variables in our crosstabulation table: employer and score. Drag one of these variables into the box labelled Row(s) (I selected employer in the figure). Next, drag the other variable of interest (score) to the box labelled Column(s) (Figure 439). Select the options indicated in the general procedure but in addition ask for expected values for each cell.
The crosstabulation table produced by SPSS Statistics (Figure 440) contains the number of cases that fall into each combination of categories. We can see that in total 28 people scored goals and of these 5 were from Sage Publications and 23 were from Sussex; 49 people didn’t score at all (63.6% of the total) and, of those, 19 worked for Sage (38.8% of the total that didn’t score) and 30 were from Sussex (61.2% of the total that didn’t score).
Before moving on to look at the test statistic itself we check that the assumption for chi-square has been met. The assumption is that in 2 × 2 tables (which is what we have here), all expected frequencies should be greater than 5. The smallest expected count is 8.7 (for Sage editors who scored). This value exceeds 5 and so the assumption has been met.
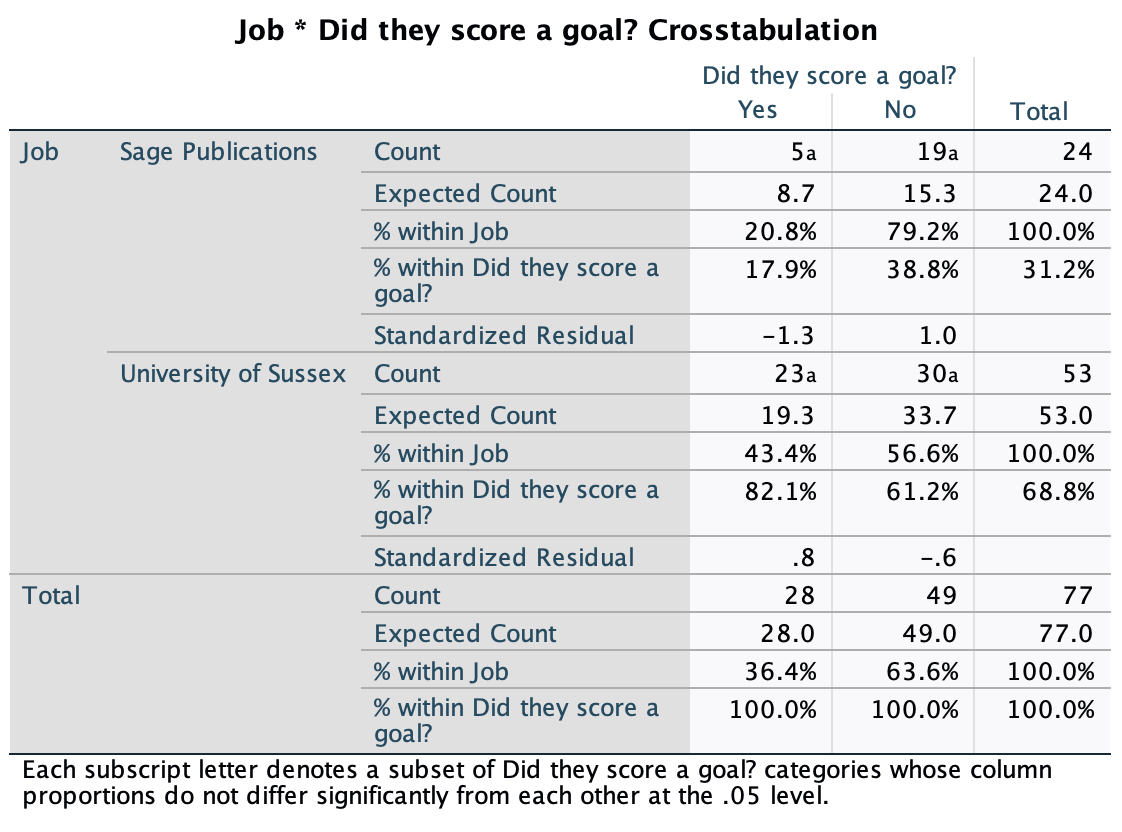
Pearson’s chi-square test examines whether there is an association between two categorical variables (in this case the job and whether the person scored or not). The value of the chi-square statistic is 3.63 (Figure 441). This value has a two-tailed significance of .057, which is bigger than .05 (hence, non-significant). Because we made a specific prediction (that Sussex people would score more than Sage people), there is a case to be made that we can halve this p-value, which would give us a significant association (because p = .0285, which is less than .05). However, as explained in the book, I’m not a big fan of one-tailed tests. In any case, we’d be well-advised to look for other information such as an effect size. Which brings us neatly onto the next task …
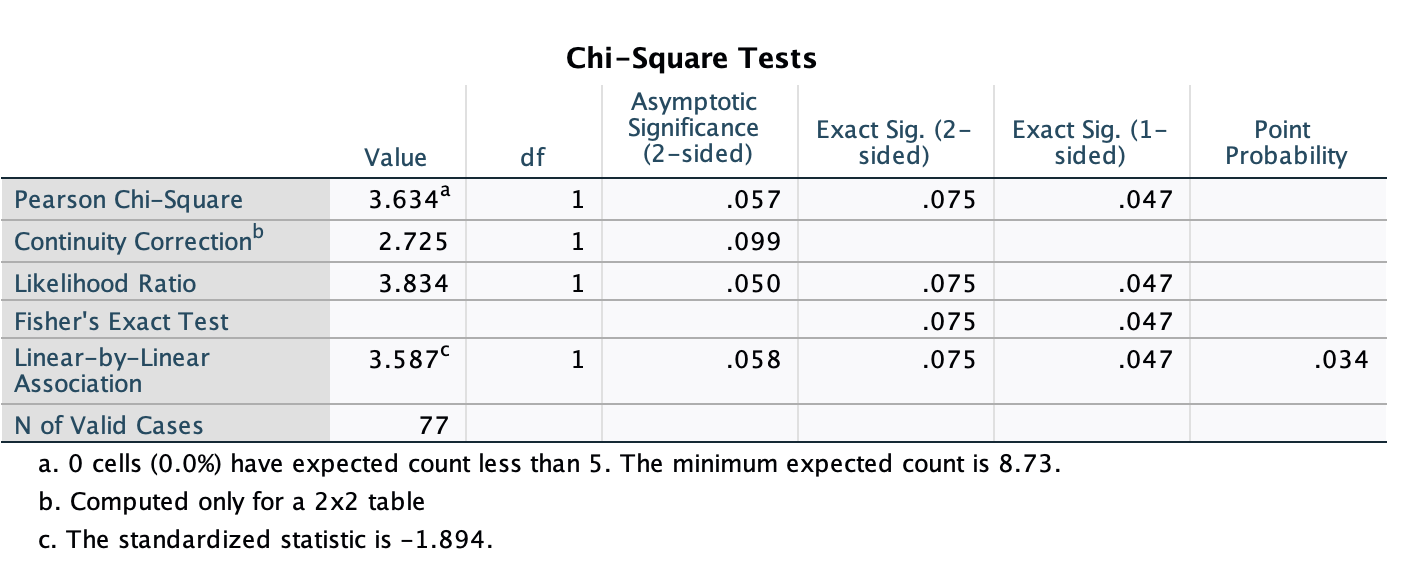
Task 19.9
Compute and interpret the odds ratio for Task 8.
The odds of someone scoring given that they were employed by SAGE are:
\[ \text{odds}_\text{scored, Sage} = \frac{5}{19}= 0.26 \]
The odds of someone scoring given that they were employed by Sussex are:
\[ \text{odds}_\text{scored, Sussex} = \frac{23}{30} = 0.77 \]
Therefore, the odds ratio is:
\[ \text{odds ratio} = \frac{\text{odds}_\text{scored, Sage}}{\text{odds}_\text{scored, Sussex}} = \frac{0.26}{0.77} = 0.34 \] The odds of scoring if you work for Sage are 0.34 times as high as if you work for Sussex; another way to express this is that if you work for Sussex, the odds of scoring are 1/0.34 = 2.95 times higher than if you work for Sage.
Task 19.10
I was interested in whether horoscopes are tosh. I recruited 2201 people, made a note of their star sign (this variable, obviously, has 12 categories: Capricorn, Aquarius, Pisces, Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio and Sagittarius) and whether they believed in horoscopes (this variable has two categories: believer or unbeliever). I sent them an identical horoscope about events in the next month, which read: ‘August is an exciting month for you. You will make friends with a tramp in the first week and cook him a cheese omelette. Curiosity is your greatest virtue, and in the second week, you’ll discover knowledge of a subject that you previously thought was boring. Statistics perhaps. You might purchase a book around this time that guides you towards this knowledge. Your new wisdom leads to a change in career around the third week, when you ditch your current job and become an accountant. By the final week you find yourself free from the constraints of having friends, your boy/girlfriend has left you for a Russian ballet dancer with a glass eye, and you now spend your weekends doing loglinear analysis by hand with a pigeon called Hephzibah for company.’ At the end of August I interviewed these people and I classified the horoscope as having come true, or not, based on how closely their lives had matched the fictitious horoscope. Conduct a loglinear analysis to see whether there is a relationship between the person’s star sign, whether they believe in horoscopes and whether the horoscope came true (
horoscope.sav).
Follow the general procedure for this chapter. First, weight cases by the variable frequency. We have three variables in our crosstabulation table: star_sign believe and true. Drag one of these variables into the box labelled Row(s) (I selected believe in the figure). Drag a second variable of interest (I chose true) to the box labelled Column(s), and drag the final variable (star_sign) to the box labelled Layer 1 of 1 (Figure 442). Select the options indicated in the general procedure but in addition ask for expected values for each cell.
The crosstabulation table produced by SPSS Statistics is too large to copy here, but it contains the number of cases that fall into each combination of categories. Although this table is quite complicated, it shows that there are roughly the same number of believers and non-believers and similar numbers of those whose horoscopes came true or didn’t. These proportions are fairly consistent also across the different star signs. There are no expected counts less than 5, so the assumption of the test is met.
To run a loglinear analysis that is consistent with my section on the theory is to select Analyze > Loglinear > Model Selection … to access the dialog box in the figure. Drag the variables that you want to include in the analysis to the box labelled Factor(s). Select each variable in the Factor(s) box and click  to activate a dialog box in which you specify the value of the minimum and maximum code that you’ve used for that variable (the figure shows these values for the variables in this dataset). When you’ve done this, click
to activate a dialog box in which you specify the value of the minimum and maximum code that you’ve used for that variable (the figure shows these values for the variables in this dataset). When you’ve done this, click  to return to main dialog box, and
to return to main dialog box, and  to fit the model (Figure 443).
to fit the model (Figure 443).
To begin with, SPSS Statistics fits the saturated model (all terms are in the model, including the highest-order interaction, in this case the star sign × believe × true interaction). The two goodness-of-fit statistics in Figure 444 (Pearson’s chi-square and the likelihood-ratio statistic) test the hypothesis that the frequencies predicted by the model (the expected frequencies) are significantly different from the actual frequencies in our data (the observed frequencies). At this stage the model fits the data perfectly, so both statistics are 0 and yield a p-value of ‘.’ (i.e., SPSS Statistics can’t compute the probability).
The next part of the output (Figure 446) tells us something about which components of the model can be removed. The first bit of the output is labelled K-Way and Higher-Order Effects, and underneath there is a table showing likelihood-ratio and chi-square statistics when K = 1, 2 and 3 (as we go down the rows of the table). The first row (K = 1) tells us whether removing the one-way effects (i.e., the main effects of star sign, believer and true) and any higher-order effects will significantly affect the fit of the model. There are lots of higher-order effects here - there are the two-way interactions and the three-way interaction - and so this is basically testing whether if we remove everything from the model there will be a significant effect on the fit of the model. This is highly significant because the p-value is given as .000, which is less than .05. The next row of the table (K = 2) tells us whether removing the two-way interactions (i.e., the star sign × believe, star sign × true, and believe × true interactions) and any higher-order effects will affect the model. In this case there is a higher-order effect (the three-way interaction) so this is testing whether removing the two-way interactions and the three-way interaction would affect the fit of the model. This is significant (p = .03, which is less than .05) indicating that if we removed the two-way interactions and the three-way interaction then this would have a significant detrimental effect on the model. The final row (K = 3) is testing whether removing the three-way effect and higher-order effects will significantly affect the fit of the model. The three-way interaction is of course the highest-order effect that we have. so this is simply testing whether removal of the three-way interaction (star sign × believe × true) will significantly affect the fit of the model. If you look at the two columns labelled Sig. then you can see that both chi-square and likelihood ratio tests agree that removing this interaction will not significantly affect the fit of the model (because p > .05).
The next part of the table expresses the same thing but without including the higher-order effects. It’s labelled K-Way Effects and lists tests for when K = 1, 2 and 3. The first row (K = 1), therefore, tests whether removing the main effects (the one-way effects) has a significant detrimental effect on the model. The p-values are less than .05, indicating that if we removed the main effects of star sign, believe and true from our model it would significantly affect the fit of the model (in other words, one or more of these effects is a significant predictor of the data). The second row (K = 2) tests whether removing the two-way interactions has a significant detrimental effect on the model. The p-values are less than .05, indicating that if we removed the star sign × believe, star sign × true and believe × true interactions then this would significantly reduce how well the model fits the data. In other words, one or more of these two-way interactions is a significant predictor of the data. The final row (K = 3) tests whether removing the three-way interaction has a significant detrimental effect on the model. The p-values are greater than .05, indicating that if we removed the star sign × believe × true interaction then this would not significantly reduce how well the model fits the data. In other words, this three-way interaction is not a significant predictor of the data. This row should be identical to the final row of the upper part of the table (the K-Way and Higher-Order Effects) because it is the highest-order effect and so in the previous table there were no higher-order effects to include in the test (look at the output and you’ll see the results are identical).
In a nutshell, this tells us that the three-way interaction is not significant: removing it from the model does not have a significant effect on how well the model fits the data. We also know that removing all two-way interactions does have a significant effect on the model, as does removing the main effects, but you have to remember that loglinear analysis should be done hierarchically and so these two-way interactions are more important than the main effects.
The Partial Associations table (Figure 446) simply breaks down the table that we’ve just looked at into its component parts. So, for example, although we know from the previous output that removing all of the two-way interactions significantly affects the model, we don’t know which of the two-way interactions is having the effect. This table tells us. We get a Pearson chi-square test for each of the two-way interactions and the main effects, and the column labelled Sig. tells us which of these effects is significant (values less than .05 are significant). We can tell from this that the star sign × believe and believe × true interactions are significant, but the star sign × true interaction is not. Likewise, we saw in the previous output that removing the one-way effects also significantly affects the fit of the model, and these findings are confirmed here because the main effect of star sign is highly significant (although this just means that we collected different amounts of data for each of the star signs!).
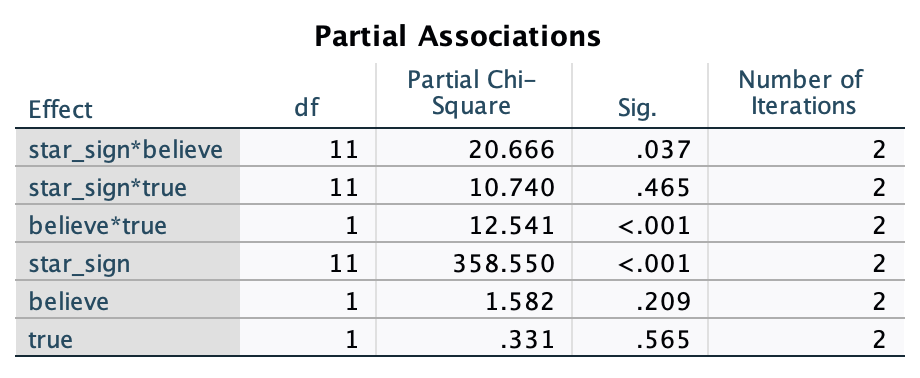
The final bit of output (Figure 447) deals with the backward elimination. SPSS Statistics begins with the highest-order effect (in this case, the star sign × believe × true interaction), remove it from the model, see what effect this has, and, if this effect is not significant, move on to the next highest effects (in this case the two-way interactions). As we’ve already seen, removing the three-way interaction does not have a significant effect, and the table labelled Step Summary confirms that removing the three-way interaction has a non-significant effect on the model. At step 1, the three two-way interactions are then assessed in the bit of the table labelled Deleted Effect. From the values of Sig. it’s clear that the star sign × believe (p = .037) and believe × true (p = .000) interactions are significant but the star sign × true interaction (p = 0. 465) is not. Therefore, at step 2 the non-significant star sign × true interaction is deleted, leaving the remaining two-way interactions in the model. These two interactions are then re-evaluated and both the star sign × believe (p = .049) and believe × true (p = .001) interactions are still significant and so are still retained. The final model is the one that retains all main effects and these two interactions. As neither of these interactions can be removed without affecting the model, and these interactions involve all three of the main effects (the variables star sign, true and believe are all involved in at least one of the remaining interactions), the main effects are not examined (because their effect is confounded with the interactions that have been retained).
Finally, SPSS Statistics evaluates this final model with the likelihood ratio statistic (Figure 448) and we’re looking for a non-significant test statistic, which indicates that the expected values generated by the model are not significantly different from the observed data (put another way, the model is a good fit of the data). In this case the result is very non-significant, indicating that the model is a good fit of the data.
Task 19.11
On my statistics module students have weekly practical statistics classes in a computer laboratory. I’ve noticed that many students are studying social media more than the very interesting statistics assignments that I have set them. I wanted to see the impact that this behaviour had on their exam performance. I collected data from all 260 students on my module. I classified their attendance as being either more or less than 50% of their practical classes, and I classified them as someone who I’d noticed sneakily looking at social_media during their class, or someone who I’d never seen looking at social media. After the exam, I noted whether they passed or failed (exam). Do a loglinear analysis to see if there is an association between looking at social media during class, attendance and failing your exam (
distracted_by_social_media.sav).
First, weight cases by the variable frequency (see the general procedure). We have three variables in our crosstabulation table: Attendance Facebook and Exam. Drag one of these variables into the box labelled Row(s) (I selected Facebook in the figure). Drag a second variable of interest (I chose Exam) to the box labelled Column(s), and drag the final variable (Attendance) to the box labelled Layer 1 of 1 (Figure 449). Select the options indicated in the general procedure but in addition ask for expected values for each cell.
The crosstabulation table (Figure 450) contains the number of cases that fall into each combination of categories. There are no expected counts less than 5, so the assumption of the test is met.
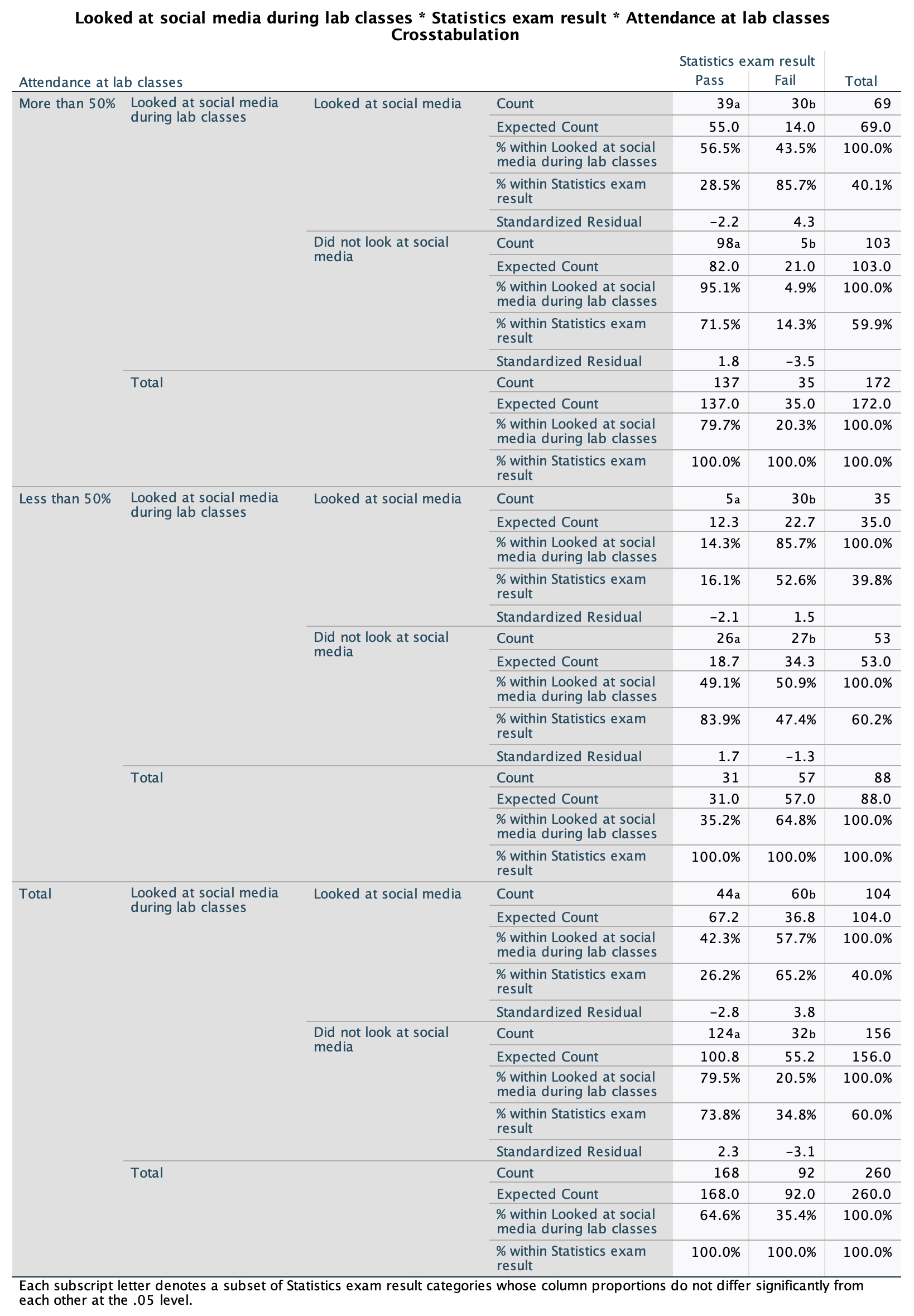
To run a loglinear analysis that is consistent with my section on the theory is to select Analyze > Loglinear > Model Selection … to access the dialog box in the figure. Drag the variables that you want to include in the analysis to the box labelled Factor(s). Select each variable in the Factor(s) box and click  to activate a dialog box in which you specify the value of the minimum and maximum code that you’ve used for that variable (the figure shows these values for the variables in this dataset). When you’ve done this, click
to activate a dialog box in which you specify the value of the minimum and maximum code that you’ve used for that variable (the figure shows these values for the variables in this dataset). When you’ve done this, click  to return to main dialog box, and
to return to main dialog box, and  to fit the model (Figure 451).
to fit the model (Figure 451).
The first bit of the output (Figure 452) labelled K-Way and Higher-Order Effects shows likelihood ratio and chi-square statistics when K = 1, 2 and 3 (as we go down the rows of the table). The first row (K = 1) tells us whether removing the one-way effects (i.e., the main effects of attendance, Facebook and exam) and any higher-order effects will significantly affect the fit of the model. There are lots of higher-order effects here - there are the two-way interactions and the three-way interaction - and so this is basically testing whether if we remove everything from the model there will be a significant effect on the fit of the model. This is highly significant because the p-value is given as .000, which is less than .05. The next row of the table (K = 2) tells us whether removing the two-way interactions (i.e., Attendance × Exam, Facebook × Exam and Attendance × Facebook) and any higher-order effects will affect the model. In this case there is a higher-order effect (the three-way interaction) so this is testing whether removing the two-way interactions and the three-way interaction would affect the fit of the model. This is significant (the p-value is given as .000, which is less than .05), indicating that if we removed the two-way interactions and the three-way interaction then this would have a significant detrimental effect on the model. The final row (K = 3) is testing whether removing the three-way effect and higher-order effects will significantly affect the fit of the model. The three-way interaction is of course the highest-order effect that we have, so this is simply testing whether removal of the three-way interaction (Attendance × Facebook × Exam) will significantly affect the fit of the model. If you look at the two columns labelled Sig. then you can see that both chi-square and likelihood ratio tests agree that removing this interaction will not significantly affect the fit of the model (because the p > .05).
The next part of the table expresses the same thing but without including the higher-order effects. It’s labelled K-Way Effects and lists tests for when K = 1, 2 and 3. The first row (K = 1), therefore, tests whether removing the main effects (the one-way effects) has a significant detrimental effect on the model. The p-values are less than .05, indicating that if we removed the main effects of Attendance, Facebook and Exam from our model it would significantly affect the fit of the model (in other words, one or more of these effects is a significant predictor of the data). The second row (K = 2) tests whether removing the two-way interactions has a significant detrimental effect on the model. The p-values are less than .05, indicating that if we removed the two-way interactions then this would significantly reduce how well the model fits the data. In other words, one or more of these two-way interactions is a significant predictor of the data. The final row (K = 3) tests whether removing the three-way interaction has a significant detrimental effect on the model. The p-values are greater than .05, indicating that if we removed the three-way interaction then this would not significantly reduce how well the model fits the data. In other words, this three-way interaction is not a significant predictor of the data. This row should be identical to the final row of the upper part of the table (the K-way and Higher-Order Effects) because it is the highest-order effect and so in the previous table there were no higher-order effects to include in the test (look at the output and you’ll see the results are identical).
We can use the information in (Figure 453) and (Figure 452) to report the results.
Chapter 20
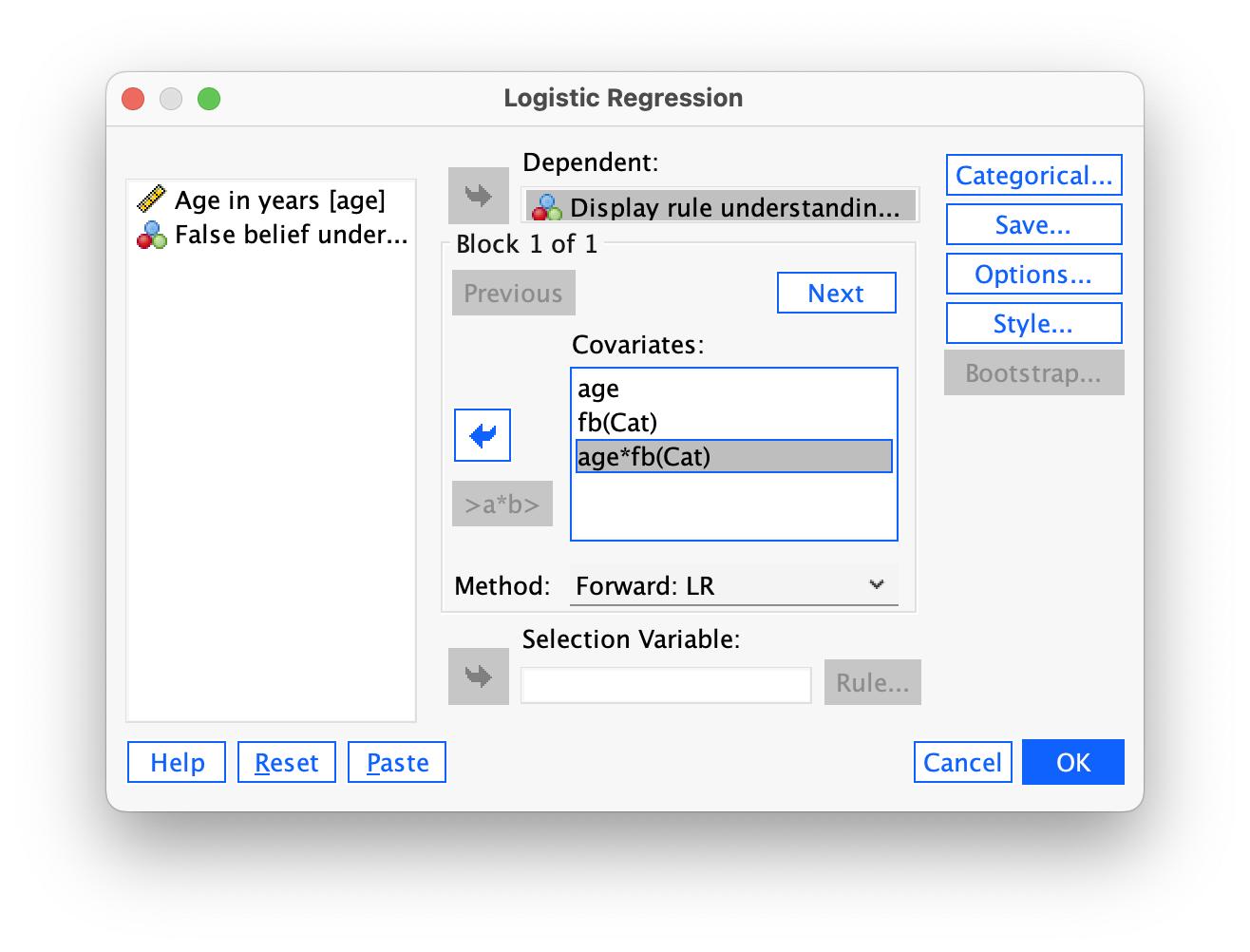
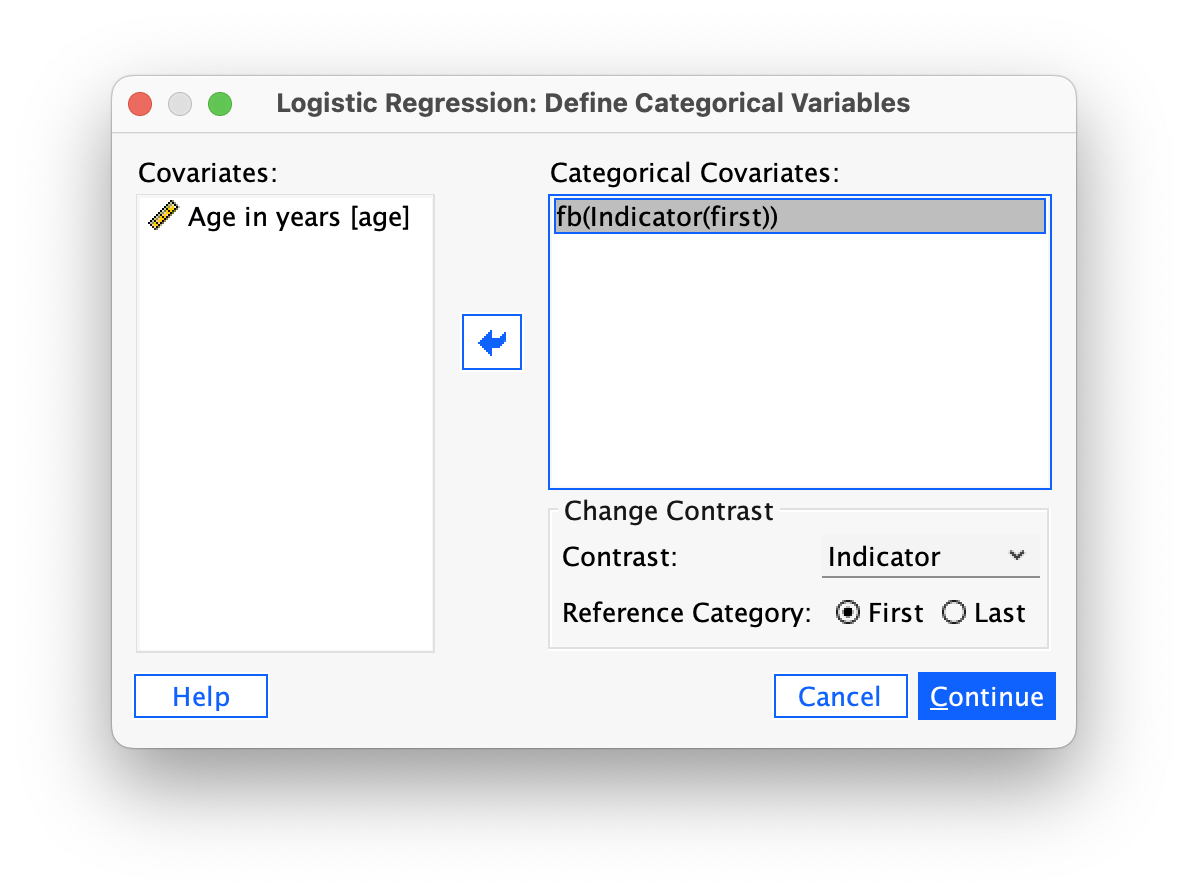
Task 20.1
A ‘display rule’ refers to displaying an appropriate emotion in a situation. For example, if you receive a present that you don’t like, you should smile politely and say ‘Thank you, Auntie Kate, I’ve always wanted a rotting cabbage’; you do not start crying and scream ‘Why did you buy me a rotting cabbage?!’ A psychologist measured children’s understanding of display rules (with a task that they could pass or fail), their age (months), and their ability to understand others’ mental states (‘theory of mind’, measured with a false belief task that they could pass or fail). Can
displayrule understanding (did the child pass the test: yes/no?) be predicted from theory of mind (did the child pass the false belief,fb, task: yes/no?),ageand their interaction? (display.sav.)
Open the file display.sav. Notice that both of the categorical variables have been entered as coding variables: the outcome variable is coded as 1 is having display rule understanding, and 0 represents an absence of display rule understanding. For the false-belief task a similar coding has been used (1 = passed the false-belief task, 0 = failed the false-belief task).
Follow the general instructions for logistic regression to fit the model. Drag display to the Dependent box, then specify the covariates (i.e., predictor variables). To specify the main effects, select one predictor (e.g. age) and then hold down Ctrl (⌘ on a mac) and select the other (fb). Transfer them to the box labelled Covariates: by clicking  . To input the interaction, again select
. To input the interaction, again select age and fb while holding down Ctrl (⌘ on a mac) but then click  . For this analysis select the Forward:LR method of regression (the main dialog box should look like the Figure 454).
. For this analysis select the Forward:LR method of regression (the main dialog box should look like the Figure 454).
In the Categorical … dialog box the covariates we specified in the main dialog box are listed on the left-hand side. Drag any categorical variables you have (in this example fb) to the Categorical Covariates:. By default SPSS Statistics uses indicator coding (i.e., the standard dummy variable coding explained in the book). This is fine for us because fb has only two categories, but to ease interpretation make sure the Reference Category is on first and click  (see Figure 455). Click to return to the main dialog box.
(see Figure 455). Click to return to the main dialog box.
In the Save … dialog box select the options shown in Figure 456. Click to return to the main dialog box. In the Options … dialog box select the options shown in Figure 457. Click to return to the main dialog box, and once there click to fit the model.
Figure 458 tells us the parameter codings given to the categorical predictor variable. We requested a forward stepwise method so the initial model is derived using only the constant in the model. The initial output tells us about the model when only the constant is included (i.e. all predictor variables are omitted). The log-likelihood of this baseline model is 96.124. This represents the fit of the model when including only the constant. Initially every child is predicted to belong to the category in which most observed cases fell. In this example there were 39 children who had display rule understanding and only 31 who did not. Therefore, of the two available options it is better to predict that all children had display rule understanding because this results in a greater number of correct predictions. Overall, the model correctly classifies 55.7% of children. The next part of the output summarizes the model, and at this stage this entails quoting the value of the constant (\(b_0\)), which is equal to 0.23.
In the first step, false-belief understanding (fb) is added to the model as a predictor (Figure 459). As such, a child is now classified as having display rule understanding based on whether they passed or failed the false-belief task. The next output shows summary statistics about the new model. The overall fit of the new model is assessed using the log-likelihood statistic (multiplied by -2 to give it a chi-square distribution, -2LL). Remember that large values of the log-likelihood statistic indicate poorly fitting statistical models.
If fb has improved the fit of the model then the value of −2LL should be less than the value when only the constant was included (because lower values of −2LL indicate better fit). When only the constant was included, −2LL = 96.124, but now fb has been included this value has been reduced to 70.042. This reduction tells us that the model is better at predicting display rule understanding than it was before fb was added. We can assess the significance of the change in a model by taking the log-likelihood of the new model and subtracting the log-likelihood of the baseline model from it. The value of the model chi-square statistic works on this principle and is, therefore, equal to −2LL with fb included minus the value of −2LL when only the constant was in the model (96.124 − 70.042 = 26.083). This value has a chi-square distribution. In this example, the value is significant at the .05 level and so we can say that overall the model predicts display rule understanding significantly better than with fb included than with only the constant included. The output also shows various \(R^2\) statistics, which we’ll return to in due course.
The classification table (Figure 460) indicates how well the model predicts group membership. The current model correctly classifies 23 children who don’t have display rule understanding but misclassifies 8 others (i.e. it correctly classifies 74.2% of cases). For children who do have display rule understanding, the model correctly classifies 33 and misclassifies 6 cases (i.e. correctly classifies 84.6% of cases). The overall accuracy of classification is, therefore, the weighted average of these two values (80%). So, when only the constant was included, the model correctly classified 56% of children, but now, with the inclusion of fb as a predictor, this has risen to 80%.

Figure 461 tells us the estimates for the coefficients for the predictors included in the model (namely, fb and the constant). The coefficient represents the change in the logit of the outcome variable associated with a one-unit change in the predictor variable. The logit of the outcome is the natural logarithm of the odds of Y occurring.
The Wald statistic has a chi-square distribution and tells us whether the b coefficient for that predictor is significantly different from zero. If the coefficient is significantly different from zero then we can assume that the predictor is making a significant contribution to the prediction of the outcome (Y). For these data it seems to indicate that false-belief understanding is a significant predictor of display rule understanding (note the significance of the Wald statistic is less than .05).

We can calculate an analogue of R using the equation in the chapter (for these data, the Wald statistic and its df are 20.856 and 1, respectively, and the original -2LL was 96.124). Therefore, R can be calculated as:
\[ R = \sqrt{\frac{20.856-(2 \times 1)}{96.124}} = 0.4429 \]
Hosmer and Lemeshow’s measure (\(R^2_{L}\)) is calculated by dividing the model chi-square by the original −2LL. In this example the model chi-square after all variables have been entered into the model is 26.083, and the original -2LL (before any variables were entered) was 96.124. So \(R^2_{L}\) = 26.083/96.124 = .271, which is different from the value we would get by squaring the value of R given above (\(R^2 = 0.4429^2 = .196\)).
Cox and Snell’s \(R^2\) is 0.311 (see earlier output), which is calculated from this equation:
\[ R_{\text{CS}}^{2} = 1 - exp\bigg(\frac{-2\text{LL}_\text{new} - (-2\text{LL}_\text{baseline})}{n}\bigg) \]
The −2LL(new) is 70.04 and −2LL(baseline) is 96.124. The sample size, n, is 70, which gives us:
\[ \begin{align} R_{\text{CS}}^{2} &= 1 - exp\bigg(\frac{70.04 - 96.124}{70}\bigg) \\ &= 1 - \exp( -0.3726) \\ &= 1 - e^{- 0.3726} \\ &= 0.311 \end{align} \]
Nagelkerke’s adjustment (see earlier output) is calculated from:
\[ \begin{align} R_{N}^{2} &= \frac{R_\text{CS}^2}{1 - \exp\bigg( -\frac{-2\text{LL}_\text{baseline}}{n} \bigg)} \\ &= \frac{0.311}{1 - \exp\big( - \frac{96.124}{70} \big)} \\ &= \frac{0.311}{1 - e^{-1.3732}} \\ &= \frac{0.311}{1 - 0.2533} \\ &= 0.416 \end{align} \]
As you can see, there’s a fairly substantial difference between the two values!
The odds ratio, exp(b) (Exp(B) in the output) is the change in odds. If the value is greater than 1 then it indicates that as the predictor increases, the odds of the outcome occurring increase. Conversely, a value less than 1 indicates that as the predictor increases, the odds of the outcome occurring decrease. In this example, we can say that the odds of a child who has false-belief understanding also having display rule understanding are 15 times higher than those of a child who does not have false-belief understanding.
In the options, we requested a confidence interval for exp(b) and it can also be found in Output 4. Remember that if we ran 100 experiments and calculated confidence intervals for the value of exp(b), then these intervals would encompass the actual value of exp(b) in the population (rather than the sample) on 95 occasions. So, assuming that this experiment was one of the 95% where the confidence interval contains the population value then the population value of exp(b) lies between 4.84 and 51.71. However, this experiment might be one of the 5% that ‘misses’ the true value.
Figure 462 shows the test statistic for fb if it were removed from the model. Removing fb would result in a change in the -2LL that is highly significant (p < .001), which means that removing fb from the model would have a significant detrimental effect on the fit of the model - in other words, it fb significantly predicts display rule understanding. We are also told about the variables currently not in the model. First of all, the residual chi-square (labelled Overall Statistics in the output), which is non-significant, tells us that none of the remaining variables have coefficients significantly different from zero. Furthermore, each variable is listed with its score statistic and significance value, and for both variables their coefficients are not significantly different from zero (as can be seen from the significance values of .128 for age and .261 for the interaction of age and false-belief understanding). Therefore, no further variables will be added to the model.
The classification plot shows the predicted probabilities of a child passing the display rule task. If the model perfectly fits the data, then this histogram should show all of the cases for which the event has occurred on the right-hand side, and all the cases for which the event hasn’t occurred on the left-hand side. In this example, the only significant predictor is dichotomous and so there are only two columns of cases on the plot. As a rule of thumb, the more that the cases cluster at each end of the plot, the better (see the book chapter for more details). In this example there are two Ns on the right of the model and one Y on the left of the model. These are misclassified cases, and the fact there are relatively few of them suggests the model is making correct predictions for most children.
Step number: 1
Observed Groups and Predicted Probabilities
80 + +
I I
I I
F I I
R 60 + +
E I I
Q I I
U I I
E 40 + Y +
N I Y I
C I Y Y I
Y I N Y I
20 + N Y +
I N Y I
I N N I
I N N I
Predicted ---------+---------+---------+---------+---------+---------+---------+---------+---------+----------
Prob: 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1
Group: NNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNNYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY
Predicted Probability is of Membership for Yes
The Cut Value is .50
Symbols: N - No
Y - Yes
Each Symbol Represents 5 Cases.The predicted probabilities and predicted group memberships will have been saved as variables in the data editor ( PRE_1 and PGR_1). These probabilities can be listed using the Analyze > Reports > Case Summaries … dialog box (see the book chapter). Figure 463 shows a selection of the predicted probabilities. Because the only significant predictor was a dichotomous variable, there are only two different probability values. The only significant predictor of display rule understanding was false-belief understanding, which could have a value of either 1 (pass the false-belief task) or 0 (fail the false-belief task). These values tells us that when a child doesn’t possess second-order false-belief understanding (fb = 0, No), there is a probability of .2069 that they will pass the display rule task, approximately a 21% chance (1 out of 5 children). However, if the child does pass the false-belief task (fb = 1, yes), there is a probability of .8049 that they will pass the display rule task, an 80.5% chance (4 out of 5 children). Consider that a probability of 0 indicates no chance of the child passing the display rule task, and a probability of 1 indicates that the child will definitely pass the display rule task. Therefore, the values obtained suggest a role for false-belief understanding as a prerequisite for display rule understanding.
Assuming we are content that the model is accurate and that false-belief understanding has some substantive significance, then we could conclude that false-belief understanding is the single best predictor of display rule understanding. Furthermore, age and the interaction of age and false-belief understanding did not significantly predict display rule understanding. This conclusion is fine in itself, but to be sure that the model is a good one, it is important to examine the residuals, which brings us nicely onto the next task.
Task 20.2
Are there any influential cases or outliers in the model for Task 1?
To answer this question we need to look at the model residuals (Figure 464). These residuals are slightly unusual because they are based on a single predictor that is categorical. This is why there isn’t a lot of variability in their values. The basic residual statistics for this example (Cook’s distance, leverage, standardized residuals and DFBeta values) show little cause for concern. Note that all cases have DFBetas less than 1 and leverage statistics (LEV_1) close to the calculated expected value of 0.03. There are also no unusually high values of Cook’s distance (COO_1) which, all in all, means that there are no influential cases having an effect on the model. For Cook’s distance you should look for values which are particularly high compared to the other cases in the sample, and values greater than 1 are usually problematic. About half of the leverage values are a little high but given that the other statistics are fine, this is probably no cause for concern. The standardized residuals all have values within ±2.5 and predominantly have values within ±2, and so there seems to be very little here to concern us.
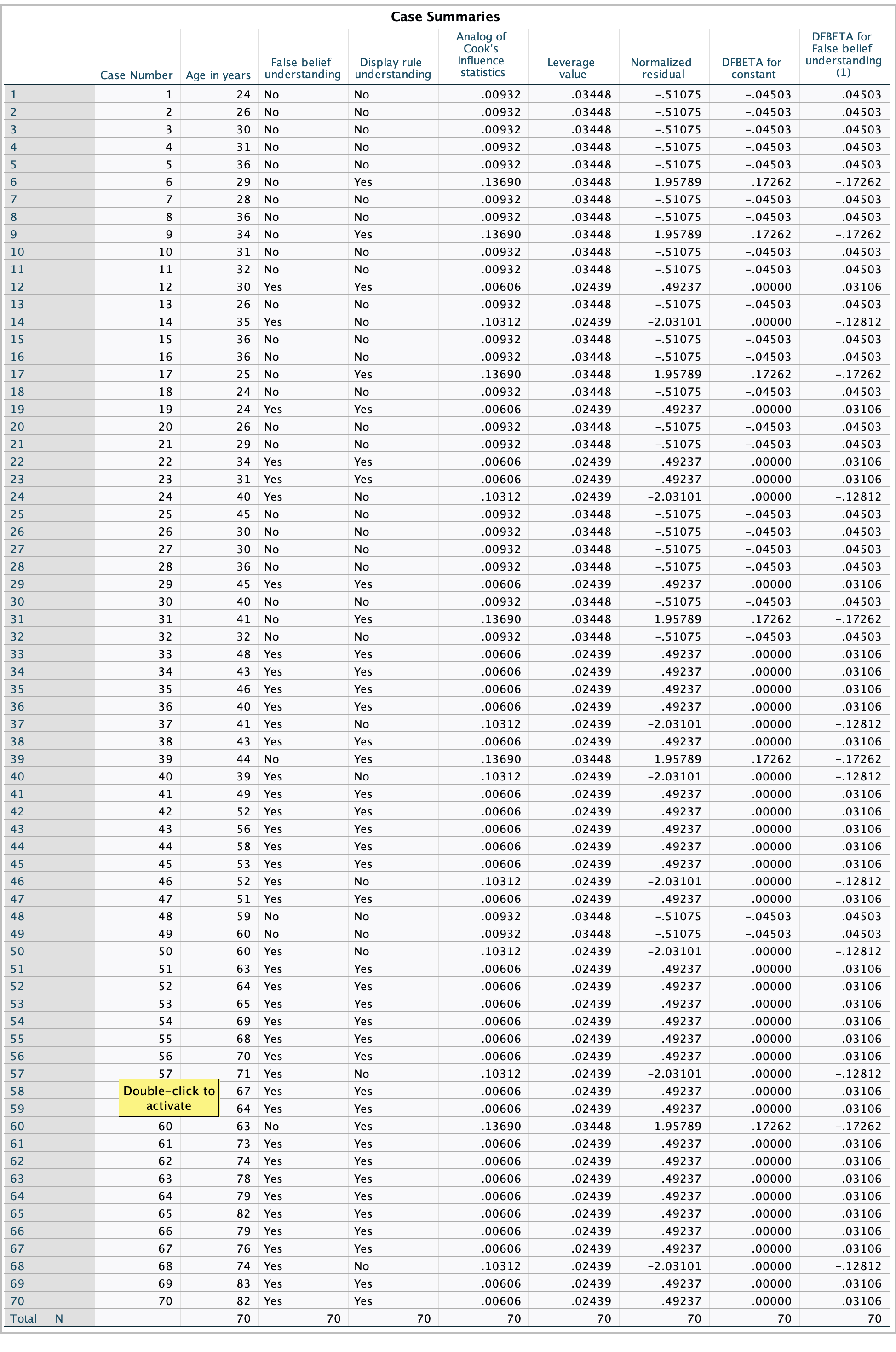
Task 20.3
The behaviour of drivers has been used to claim that people of a higher social class are more unpleasant (Piff et al., 2012). Piff and colleagues classified social class by the type of car (
vehicle) on a five-point scale and observed whether the drivers cut in front of other cars at a busy intersection (vehicle_cut). Do a logistic regression to see whether social class predicts whether a driver cut in front of other vehicles (piff_2012_vehicle.sav).
Follow the general instructions for logistic regression to fit the model. The main dialog box should look like the figure below.
The first block of output (Figure 466) tells us about the model when only the constant is included.In this example there were 34 participants who did cut off other vehicles at intersections and 240 who did not. Therefore, of the two available options it is better to predict that all participants did not cut off other vehicles because this results in a greater number of correct predictions. The contingency table for the model in this basic state shows that predicting that all participants did not cut off other vehicles results in 0% accuracy for those who did cut off other vehicles, and 100% accuracy for those who did not. Overall, the model correctly classifies 87.6% of participants.
The table labelled Variables in the Equation at this stage contains only the constant, which has a value of \(b_0 = −1.95\). The table labelled Variables not in the Equation. The bottom line of this table reports the residual chi-square statistic (labelled Overall Statistics) as 4.01 which is only just significant at p = .045. This statistic tells us that the coefficient for the variable not in the model is significantly different from zero - in other words, that the addition of this variable to the model will significantly improve its fit.
The next part of the output (Figure 467) deals with the model after the predictor variable (vehicle) has been added to the model. As such, a person is now classified as either cutting off other vehicles at an intersection or not, based on the type of vehicle they were driving (as a measure of social status). The output shows summary statistics about the new model. The overall fit of the new model is significant because the Model chi-square in the table labelled Omnibus Tests of Model Coefficients is significant, \(\chi^2\)(1) = 4.16, p = .041. Therefore, the model that includes the variable vehicle predicted whether or not participants cut off other vehicles at intersections better than the model that includes only the constant.

The classification table (Figure 468) indicates how well the model predicts group membership. In step 1, the model correctly classifies 240 participants who did not cut off other vehicles and does not misclassify any (i.e. it correctly classifies 100% of cases). For participants who do did cut off other vehicles, the model correctly classifies 0 and misclassifies 34 cases (i.e. correctly classifies 0% of cases). The overall accuracy of classification is, therefore, the weighted average of these two values (87.6%). Therefore, the accuracy is no different than when only the constant was included in the model.
Figure 469 shows that the significance of the Wald statistic is .047, which is less than .05. Therefore, we can conclude that the status of the vehicle the participant was driving significantly predicted whether or not they cut off another vehicle at an intersection. However, I’d interpret this significance in the context of the classification table, which showed us that adding the predictor of vehicle did not result in any more cases being more accurately classified.
The exp b (Exp(*B*) in the output) is the change in odds of the outcome resulting from a unit change in the predictor. In this example, the exp b for vehicle in step 1 is 1.441, which is greater than 1, indicating that as the predictor (vehicle) increases, the value of the outcome also increases, that is, the value of the categorical variable moves from 0 (did not cut off vehicle) to 1 (cut off vehicle). In other words, drivers of vehicles of a higher status were more likely to cut off other vehicles at intersections.
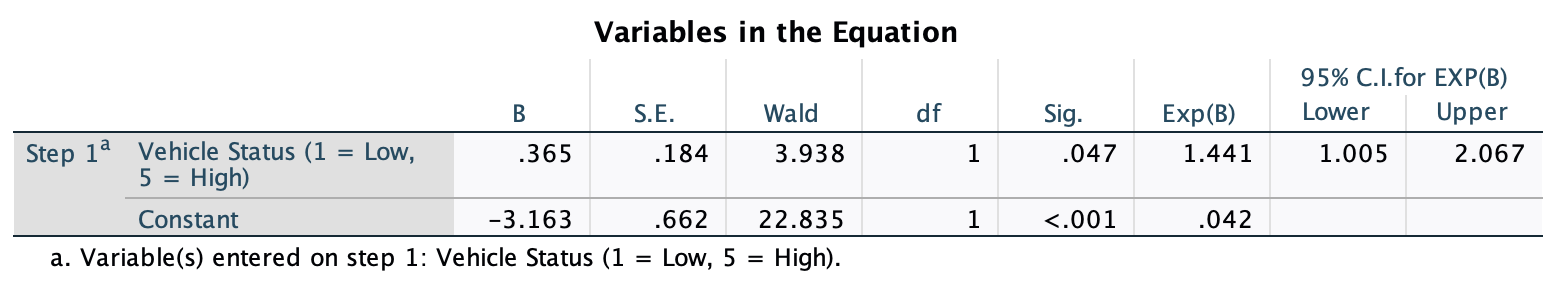
Task 20.4
In a second study, Piff et al. (2012) observed the behaviour of drivers and classified social class by the type of car (
vehicle), but the outcome was whether the drivers cut off a pedestrian at a crossing (pedestrian_cut). Do a logistic regression to see whether social class predicts whether or not a driver prevents a pedestrian from crossing (piff_2012_pedestrian.sav).
Follow the general instructions for logistic regression to fit the model. The main dialog box should look like Figure 470.
The first block of output (Figure 471) tells us about the model when only the constant is included. In this example there were 54 participants who did cut off pedestrians at intersections and 98 who did not. Therefore, of the two available options it is better to predict that all participants did not cut off other vehicles because this results in a greater number of correct predictions. The contingency table for the model in this basic state shows that predicting that all participants did not cut off pedestrians results in 0% accuracy for those who did cut off pedestrians, and 100% accuracy for those who did not. Overall, the model correctly classifies 64.5% of participants.
The table labelled Variables in the Equation at this stage contains only the constant, which has a value of \(b_0 = −0.596\). The table labelled Variables not in the Equation. The bottom line of this table reports the residual chi-square statistic (labelled Overall Statistics) as 4.77 which is only just significant at p = .029. This statistic tells us that the coefficient for the variable not in the model is significantly different from zero - in other words, that the addition of this variable to the model will significantly improve its fit.
The next part of the output (Figure 472) deals with the model after the predictor variable (vehicle) has been added to the model. As such, a person is now classified as either cutting off pedestrians at an intersection or not, based on the type of vehicle they were driving (as a measure of social status). The output shows summary statistics about the new model. The overall fit of the new model is significant because the Model chi-square in the table labelled Omnibus Tests of Model Coefficients is significant, \(\chi^2\)(1) = 4.86, p = .028. Therefore, the model that includes the variable vehicle predicted whether or not participants cut off pedestrians at intersections better than the model that includes only the constant.

The classification table (Figure 473) indicates how well the model predicts group membership. In step 1, the model correctly classifies 91 participants who did not cut off pedestrians and does not misclassify any (i.e. it correctly classifies 92.9% of cases). For participants who do did cut off pedestrians, the model correctly classifies 6 and misclassifies 48 cases (i.e. correctly classifies 11.1% of cases). The overall accuracy of classification is the weighted average of these two values (63.8%). Therefore, the accuracy (0verall) has decreased slightly (from 64.5% to 63.8%).
Figure 474 shows that the significance of the Wald statistic is .031, which is less than .05. Therefore, we can conclude that the status of the vehicle the participant was driving significantly predicted whether or not they cut off pedestrians at an intersection. The exp b (Exp(B) in the output) is the change in odds of the outcome resulting from a unit change in the predictor. In this example, the exp b for vehicle in step 1 is 1.495, which is greater than 1, indicating that as the predictor (vehicle) increases, the value of the outcome also increases, that is, the value of the categorical variable moves from 0 (did not cut off pedestrian) to 1 (cut off pedestrian). In other words, drivers of vehicles of a higher status were more likely to cut off pedestrians at intersections.

Task 20.5
Four hundred and sixty-seven lecturers completed questionnaire measures of
burnout(burnt out or not), perceivedcontrol(high score = low perceived control),copingability (high score = high ability to cope with stress), stress fromteaching(high score = teaching creates a lot of stress for the person), stress fromresearch(high score = research creates a lot of stress for the person) and stress from providingpastoralcare (high score = providing pastoral care creates a lot of stress for the person). Cooper et al. (1988) model of stress indicates that perceived control and coping style are important predictors of burnout. The remaining predictors were measured to see the unique contribution of different aspects of a lecturer’s work to their burnout. Conduct a logistic regression to see which factors predict burnout. (burnout.sav).
Follow the general instructions for logistic regression to fit the model. The model should be fit hierarchically because Cooper’s model indicates that perceived control and coping style are important predictors of burnout. So, these variables should be entered in the first block (Figure 475).
The second block should contain all other variables, and because we don’t know anything much about their predictive ability, we might enter them in a stepwise fashion (I chose Forward: LR) as in Figure 476.
At step 1 (Figure 477), the overall fit of the model is significant, \(\chi^2\)(2) = 165.93, p < .001. The model accounts for 29.9% or 44.1% of the variance in burnout (depending on which measure of \(R^2\) you use).
At step 2 (Figure 478), the overall fit of the model is significant after both the first new variable (teaching), \(\chi^2\)(3) = 193.34, p < .001, and second new variable (pastoral) have been entered, \(\chi^2\)(4) = 205.40, p < .001. The final model accounts for 35.6% or 52.4% of the variance in burnout (depending on which measure of \(R^2\) you use).
Task 20.6
An HIV researcher explored the factors that influenced condom use with a new partner (relationship less than 1 month old). The outcome measure was whether a condom was used (use: condom used = 1, not used = 0). The predictor variables were mainly scales from the Condom Attitude Scale (Sacco et al., 1991):
gender; the degree to which the person views their relationship as ‘safe’ from sexually transmitted disease (safety); the degree to which previous experience influences attitudes towards condom use (experience); whether or not the couple used a condom in their previous encounter (previous: 1 = condom used, 0 = not used, 2 = no previous encounter with this partner); the degree of self-control that a person has when it comes to condom use (self_control); the degree to which the person perceives a risk from unprotected sex (risk_perception). Previous research has shown that gender, relationship safety and perceived risk predict condom use (Sacco et al., 1991). Verify these previous findings and test whether self-control, previous usage and sexual experience predict condom use (condom.sav).
Follow the general instructions for logistic regression to fit the model. We run a hierarchical logistic regression entering perceive, safety and gender in the first block:
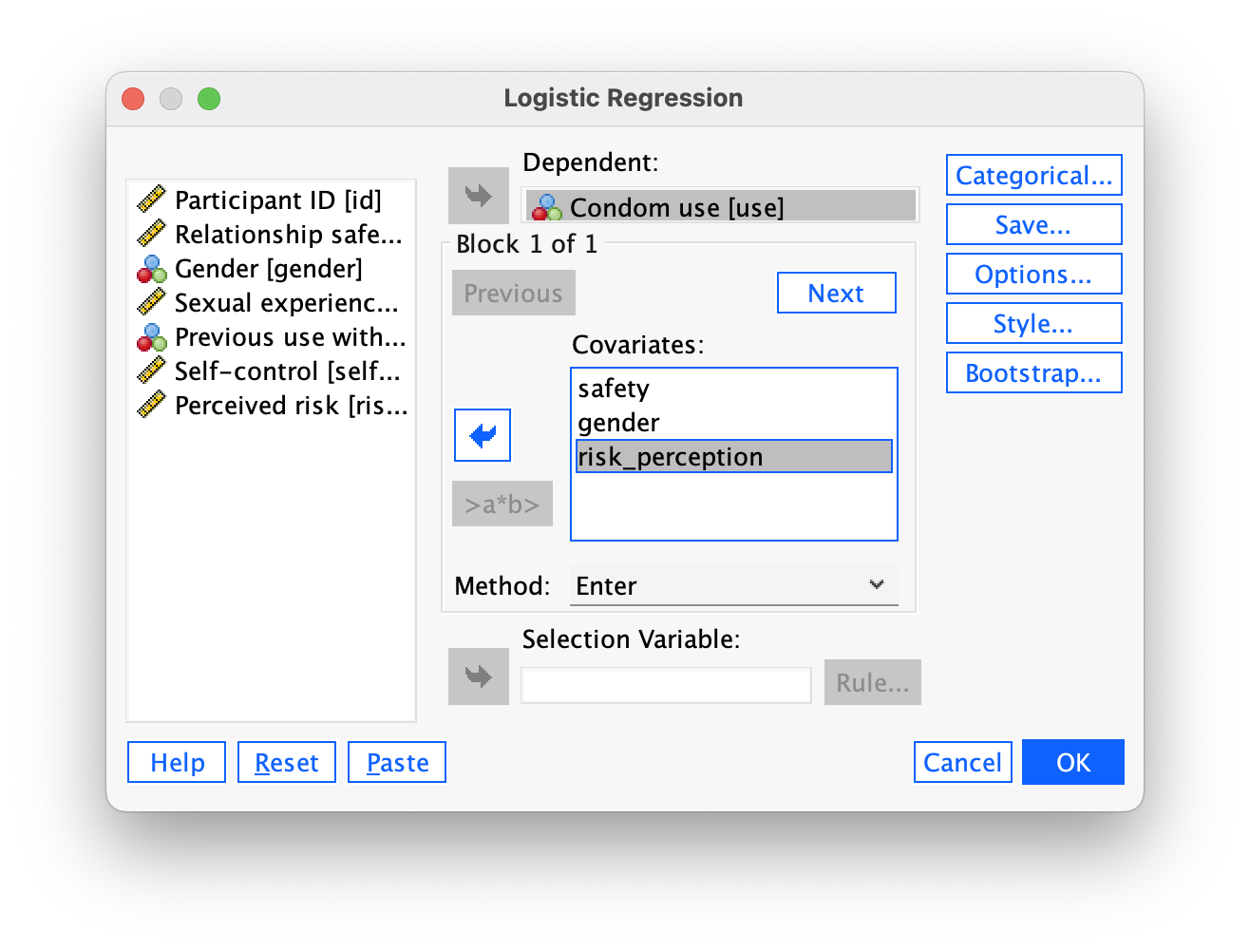
In the second block we add previous, selfcon and sexexp. I used forced entry on both blocks:
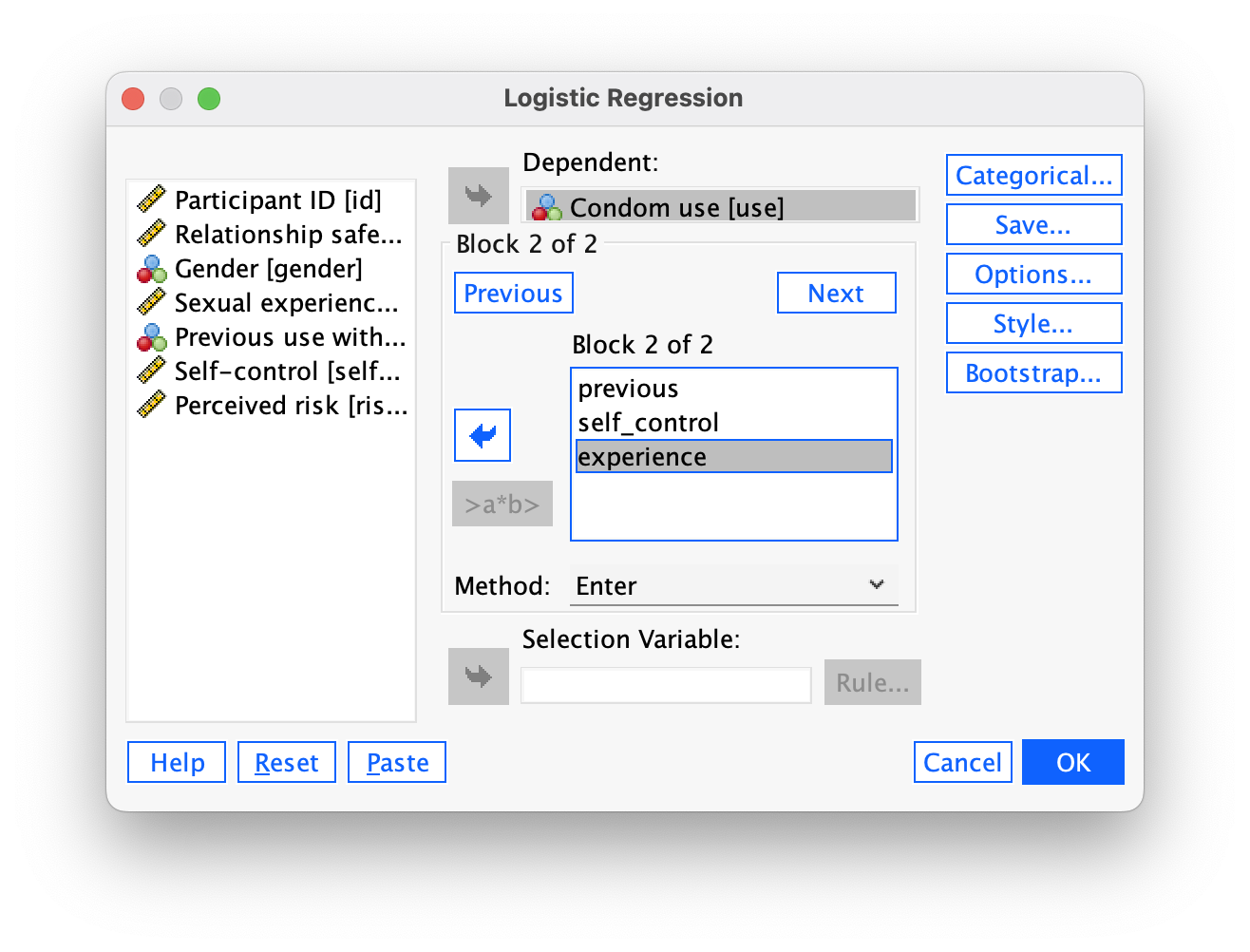
For the variable previous I used an indicator contrast with ‘No condom’ (the first category) as the base category. I left gender with the default indicator coding:
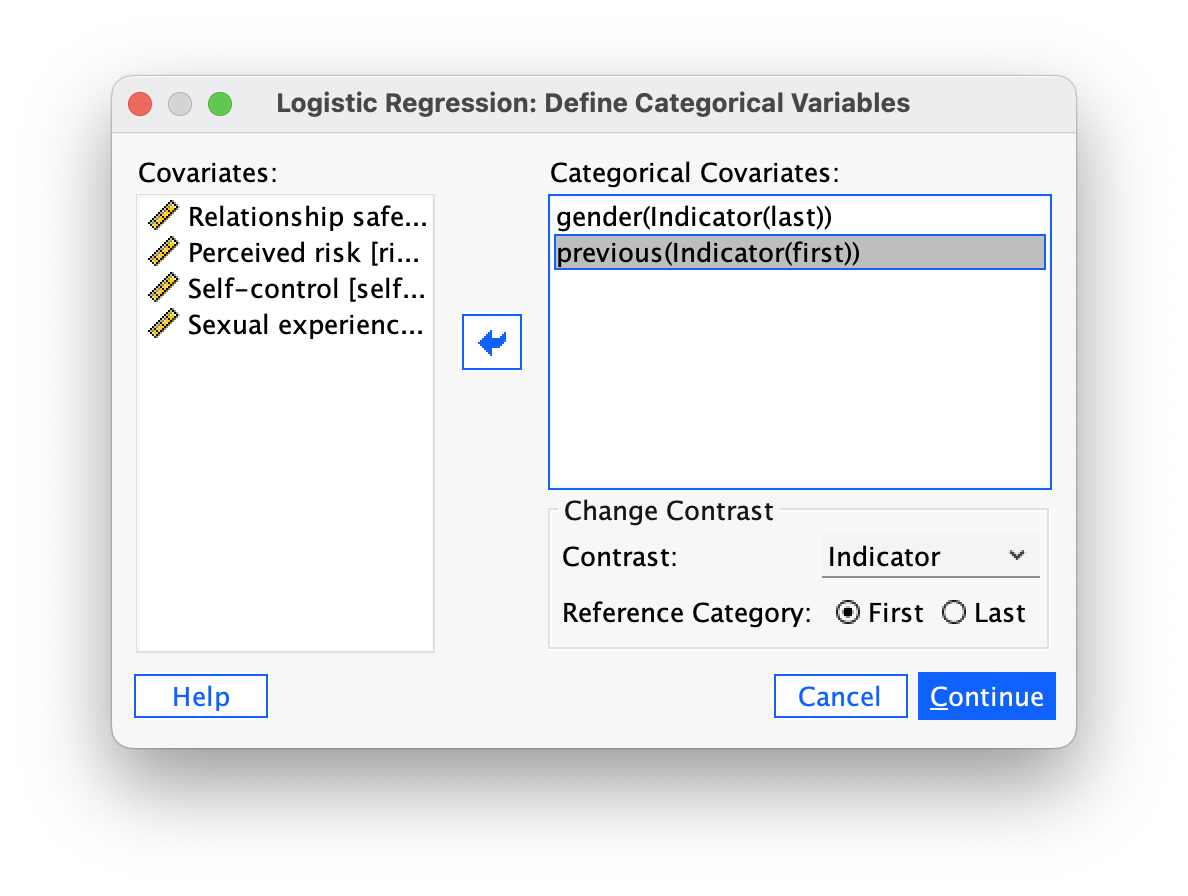
In this analysis we forced perceive, safety and gender into the model first. The first output (Figure 482) tells us that 100 cases have been accepted, that the dependent variable has been coded 0 and 1 (because this variable was coded as 0 and 1 in the data editor, these codings correspond exactly to the data itself). 57% of cases are correctly classified with no predictors in the model.
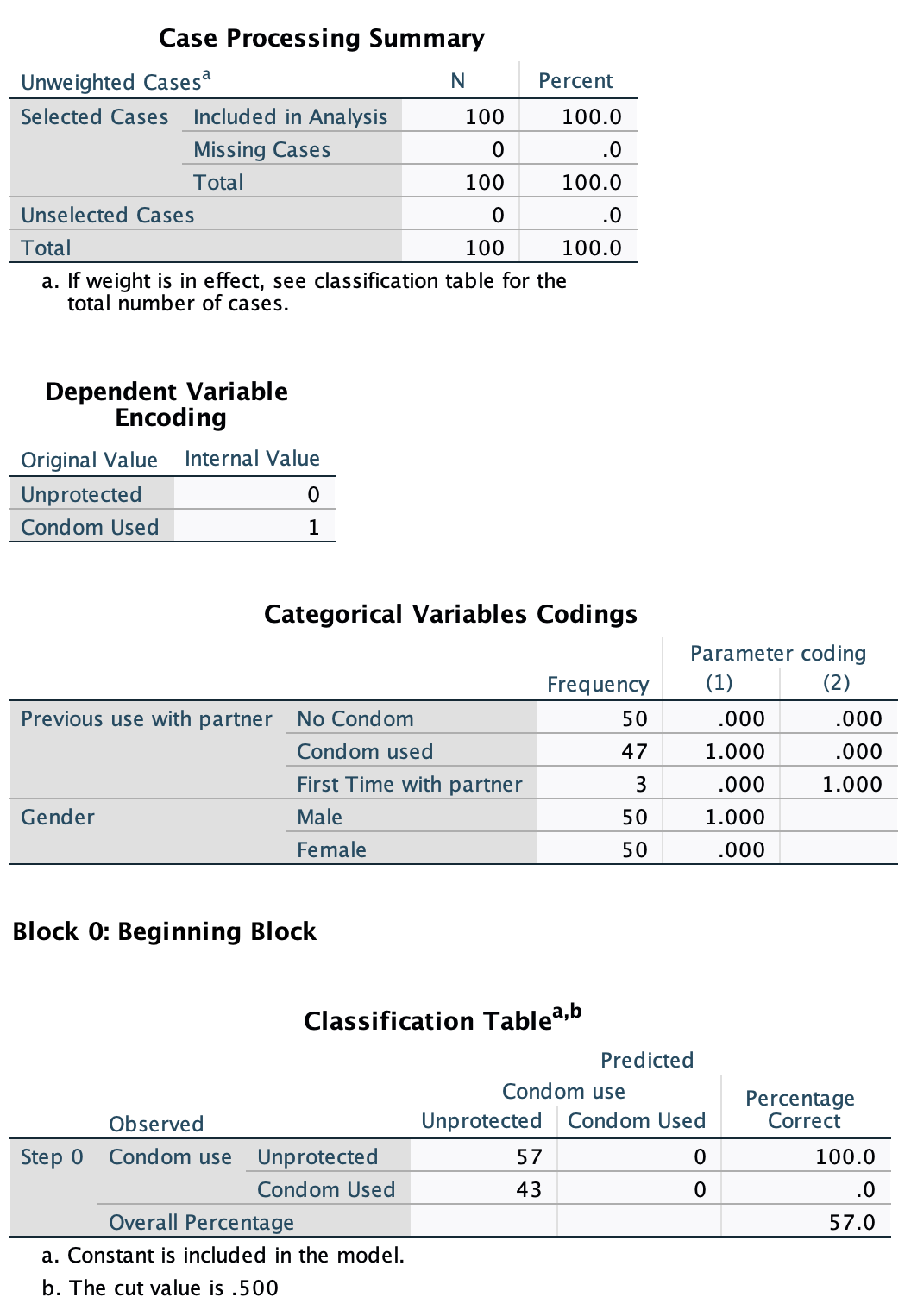
The output for block 1 (Figure 483) provides information about the model after the variables perceive, safety and gender have been added. The −2LL has dropped to 105.77, which is a change of 30.89 (the model chi-square). This value tells us about the model as a whole, whereas the block tells us how the model has improved since the last block. The change in the amount of information explained by the model is significant (\(\chi^2\)(3) = 30.89, p < .001) and so using perceived risk, relationship safety and gender as predictors significantly improves our ability to predict condom use. Finally, the classification table shows us that 74% of cases can be correctly classified using these three predictors.
Hosmer and Lemeshow’s goodness-of-fit test statistic tests the hypothesis that the observed data are significantly different from the predicted values from the model. So, in effect, we want a non-significant value for this test (because this would indicate that the model does not differ significantly from the observed data). In this case (\(\chi^2\)(8) = 9.70, p = .287) it is non-significant, which is indicative of a model that is predicting the real-world data fairly well.
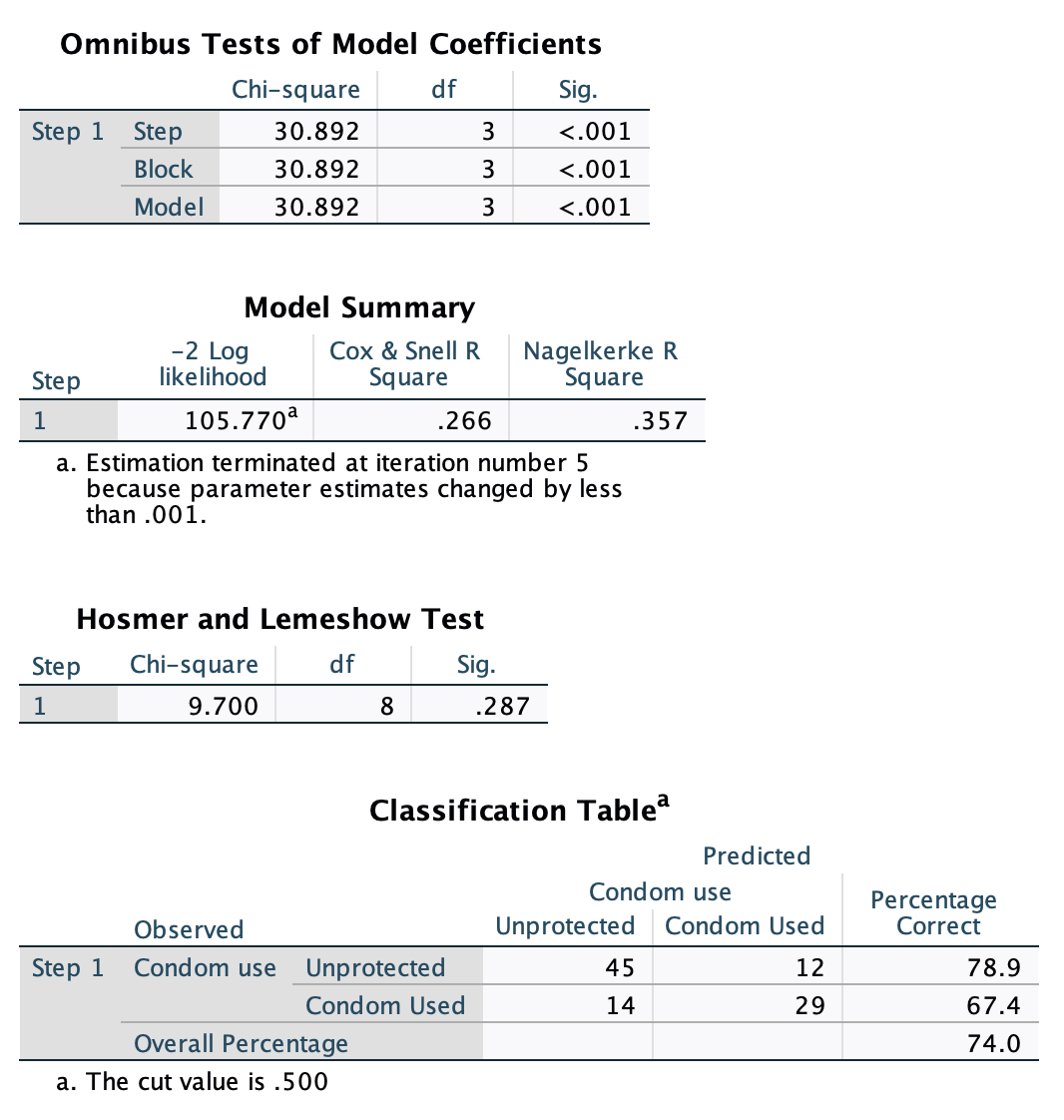
The table labelled Variables in the Equation tells us the parameters of the model for the first block (Figure 484). The significance values of the Wald statistics for each predictor indicate that both perceived risk (Wald = 17.78, p < .001) and relationship safety (Wald = 4.54, p = .033) significantly predict condom use. Gender, however, does not (Wald = 0.41, p = .523).
The odds ratio for perceived risk (Exp(B) = 2.56 [1.65, 3.96] indicates that if the value of perceived risk goes up by 1, then the odds of using a condom also increase (because Exp(B) is greater than 1). The confidence interval for this value ranges from 1.65 to 3.96, so if this is one of the 95% of samples for which the confidence interval contains the population value the value of Exp(B) in the population lies somewhere between these two values. In short, as perceived risk increase by 1, people are just over twice as likely to use a condom.
The odds ratio for relationship safety (Exp(B) = 0.63 [0.41, 0.96] indicates that if the relationship safety increases by one point, then the odds of using a condom decrease (because Exp(B) is less than 1). The confidence interval for this value ranges from 0.41 to 0.96, so if this is one of the 95% of samples for which the confidence interval contains the population value the value of Exp(B) in the population lies somewhere between these two values. In short, as relationship safety increases by one unit, subjects are about 1.6 times less likely to use a condom.
The odds ratio for gender (Exp(B) = 0.729 [0.28, 1.93] indicates that as gender changes from 1 (female) to 0 (male), then the odds of using a condom decrease (because Exp(B) is less than 1). The confidence interval for this value crosses 1. Assuming that this is one of the 95% of samples for which the confidence interval contains the population value this means that the direction of the effect in the population could indicate either a positive (Exp(B) > 1) or negative (Exp(B) < 1) relationship between gender and condom use.
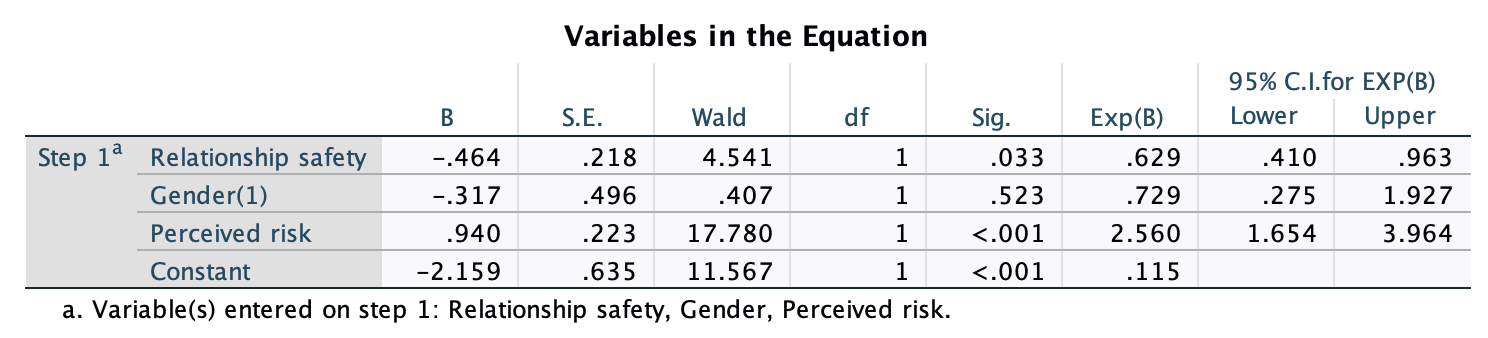
A glance at the classification plot brings not such good news because a lot of cases are clustered around the middle. This pattern indicates that the model could be making better predictions (there are currently a lot of cases that have a probability of condom use at around 0.5).
Step number: 1
Observed Groups and Predicted Probabilities
16 + +
I I
I I
F I I
R 12 + C +
E I C C I
Q I C C I
U I C C I
E 8 + C C C +
N I C C C I
C I U C C C C I
Y I U C U U U C C C I
4 + U U U U U U C U C +
I U U U U C C U U U U C C I
IU U UU U U U C U U U U U U U U CC C C C C I
IU U UUUU U U UC U U U U U U CU U CU U U C C C U C CU C I
Predicted ---------+---------+---------+---------+---------+---------+---------+---------+---------+----------
Prob: 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1
Group: UUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
Predicted Probability is of Membership for Condom Used
The Cut Value is .50
Symbols: U - Unprotected
C - Condom Used
Each Symbol Represents 1 Case.The output for block 2 (Figure 485) shows what happens to the model when our new predictors are added (previous use, self-control and sexual experience).So, we begin with the model that we had in block 1 and we then add previous, selfcon and sexexp to it. The effect of adding these predictors to the model is to reduce the –2 log-likelihood to 87.97 (a reduction of 48.69 from the original model (the model chi-square) and an additional reduction of 17.80 from block 1 (the block statistics). This additional improvement of block 2 is significant (\(\chi^2\)(4) = 17.80, p < .001), which tells us that including these three new predictors in the model has significantly improved our ability to predict condom use. The classification table tells us that the model is now correctly classifying 78% of cases. Remember that in block 1 there were 74% correctly classified and so an extra 4% of cases are now classified (not a great deal more – in fact, examining the table shows us that only four extra cases have now been correctly classified).
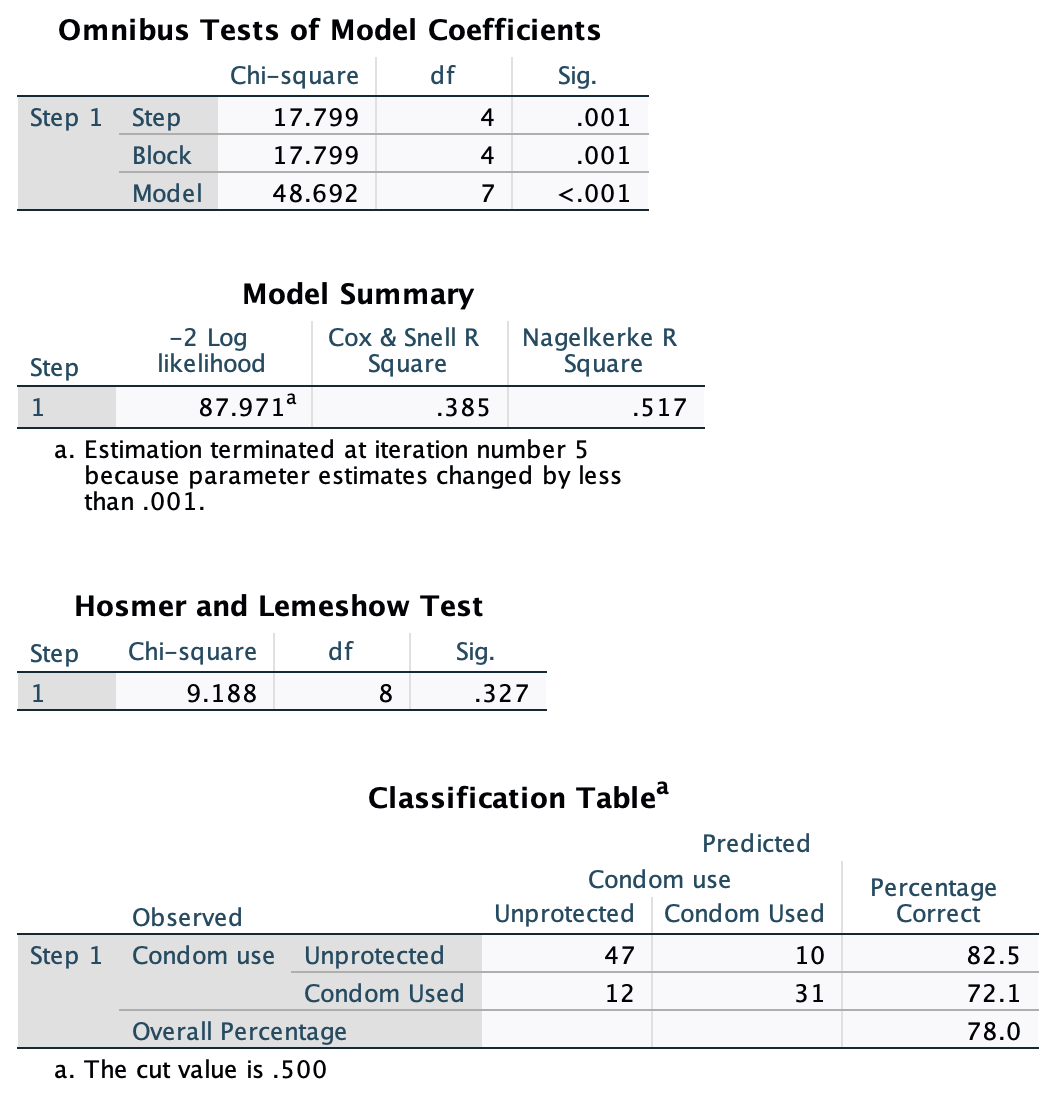
The table labelled Variables in the Equation contains details of the final model (Figure 486). The significance values of the Wald statistics for each predictor indicate that both perceived risk (Wald = 16.04, p < .001) and relationship safety (Wald = 4.17, p = .041) still significantly predict condom use and, as in block 1, gender does not (Wald = 0.00, p = .996).
Previous use has been split into two components (according to whatever contrasts were specified for this variable). Looking at the very first output, we are told the parameter codings for previous(1) and previous(2). From the output we can see that previous(1) compares the condom used group against the no condom used group, and previous(2) compares the first time with partner against the no condom used group. Therefore we can tell that (1) using a condom on the previous occasion does predict use on the current occasion (Wald = 3.88, p = .049); and (2) there is no significant diference between not using a condom on the previous occasion and this being the first time (Wald = 0.00, p = .991). Of the other new predictors we find that self-control predicts condom use (Wald = 7.51, p = .006) but sexual experience does not (Wald = 2.61, p = .106).
The odds ratio for perceived risk (Exp(B) = 2.58[1.62, 4.11] indicates that if the value of perceived risk goes up by 1, then the odds of using a condom also increase (because Exp(B) is greater than 1). The confidence interval for this value ranges from 1.62 to 4.11, so if this is one of the 95% of samples for which the confidence interval contains the population value the value of Exp(B) in the population lies somewhere between these two values. In short, as perceived risk increase by 1, people are just over twice as likely to use a condom.
The odds ratio for relationship safety (Exp(B) = 0.62 [0.39, 0.98] indicates that if the relationship safety increases by one point, then the odds of using a condom decrease (because Exp(B) is less than 1). The confidence interval for this value ranges from 0.39 to 0.98, so if this is one of the 95% of samples for which the confidence interval contains the population value the value of Exp(B) in the population lies somewhere between these two values. In short, as relationship safety increases by one unit, subjects are about 1.6 times less likely to use a condom.
The odds ratio for gender (Exp(B) = 0.996 [0.33, 3.07] indicates that as gender changes from 1 (female) to 0 (male), then the odds of using a condom decrease (because Exp(B) is less than 1). The confidence interval for this value crosses 1. Assuming that this is one of the 95% of samples for which the confidence interval contains the population value this means that the direction of the effect in the population could indicate either a positive (Exp(B) > 1) or negative (Exp(B) < 1) relationship between gender and condom use.
The odds ratio for previous(1) (Exp(B) = 2.97[1.01, 8.75) indicates that if the value of previous usage goes up by 1 (i.e., changes from not having used one to having used one), then the odds of using a condom also increase. If this is one of the 95% of samples for which the confidence interval contains the population value then the value of Exp(B) in the population lies somewhere between 1.01 and 8.75. In other words it is a positive relationship: previous use predicts future use. For previous(2) the odds ratio (Exp(B) = 0.98 [0.06, 15.29) indicates that if the value of previous usage goes changes from not having used one to this being the first time with this partner), then the odds of using a condom do not change (because the value is very nearly equal to 1). If this is one of the 95% of samples for which the confidence interval contains the population value then the value of Exp(B) in the population lies somewhere between 0.06 and 15.29 and because this interval contains 1 it means that the population relationship could be either positive or negative (and very wide ranging).
The odds ratio for self-control (Exp(B) = 1.42 [1.10, 1.82] indicates that if self-control increases by one point, then the odds of using a condom increase also. As self-control increases by one unit, people are about 1.4 times more likely to use a condom. If this is one of the 95% of samples for which the confidence interval contains the population value then the value of Exp(B) in the population lies somewhere between 1.10 and 1.82. In other words it is a positive relationship
Finally, the odds ratio for sexual experience (Exp(B) = 1.20[0.95, 1.49] indicates that as sexual experience increases by one unit, people are about 1.2 times more likely to use a condom. If this is one of the 95% of samples for which the confidence interval contains the population value then the value of Exp(B) in the population lies somewhere between 0.06 and 15.29 and because this interval contains 1 it means that the population relationship could be either positive or negative.
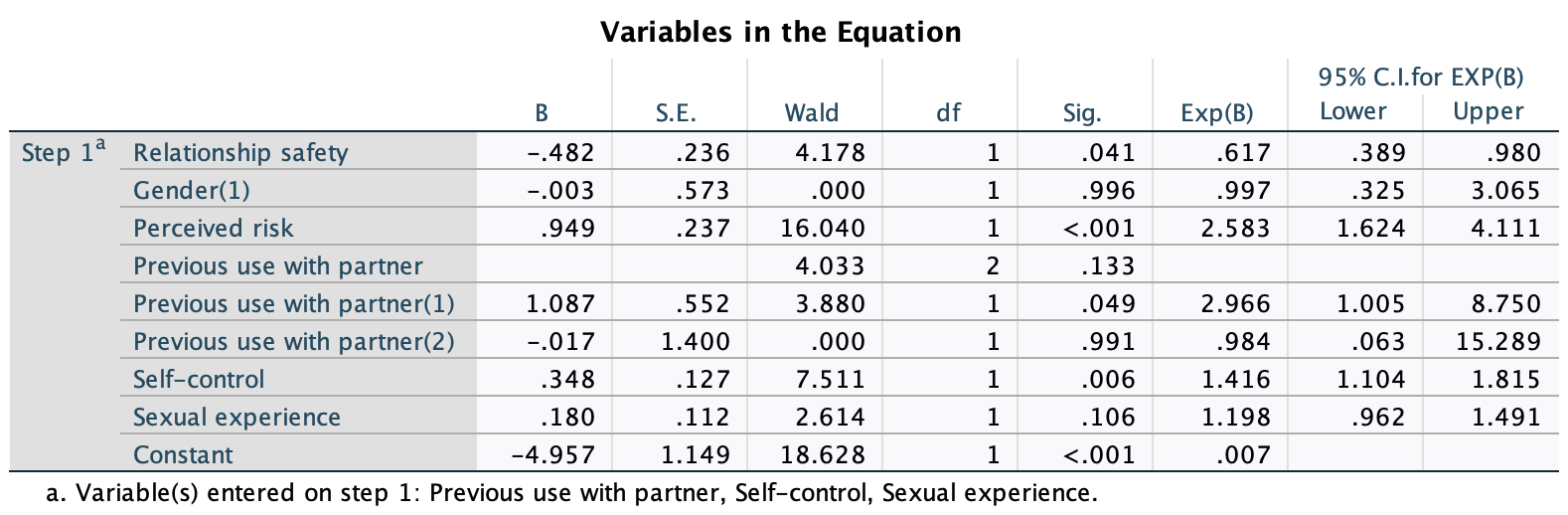
A glance at the classification plot brings better news because a lot of cases that were clustered in the middle are now spread towards the edges. Therefore, overall this new model is more accurately classifying cases compared to block 1.
Step number: 1
Observed Groups and Predicted Probabilities
8 + +
I I
I I
F I I
R 6 + U +
E I U I
Q I U I
U I U I
E 4 + UU C +
N I UU C I
C I UU U U C U C C C C I
Y I UU U U C U C C C C I
2 + UU U U UU U UU C U U C C U C C C C C CC C +
I UU U U UU U UU C U U C C U C C C C C CC C I
IUUUUUU UUUUU CCCUUUUUUU U U UU U CU U CUCUC U U C C U UU CU C CC U CC C C CC C U UCCCC CC I
IUUUUUU UUUUU CCCUUUUUUU U U UU U CU U CUCUC U U C C U UU CU C CC U CC C C CC C U UCCCC CC I
Predicted ---------+---------+---------+---------+---------+---------+---------+---------+---------+----------
Prob: 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1
Group: UUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
Predicted Probability is of Membership for Condom Used
The Cut Value is .50
Symbols: U - Unprotected
C - Condom Used
Each Symbol Represents .5 Cases.Task 20.7
How reliable is the model in Task 6?
First, we’ll check for multicollinearity (see the book for how to do this) using the output in Figure 487. The tolerance values for all variables are close to 1 and VIF values are much less than 10, which suggests no collinearity issues. The table labelled Collinearity Diagnostics shows the eigenvalues of the scaled, uncentred cross-products matrix, the condition index and the variance proportions for each predictor. If the eigenvalues are fairly similar then the derived model is likely to be unchanged by small changes in the measured variables. The condition indexes represent the square root of the ratio of the largest eigenvalue to the eigenvalue of interest (so, for the dimension with the largest eigenvalue, the condition index will always be 1). The variance proportions shows the proportion of the variance of each predictor’s b that is attributed to each eigenvalue. In terms of collinearity, we are looking for predictors that have high proportions on the same small eigenvalue, because this would indicate that the variances of their b coefficients are dependent (see the main textbook for more detail). No variables have similarly high variance proportions for the same dimensions. The result of this output suggests that there is no problem of collinearity in these data.
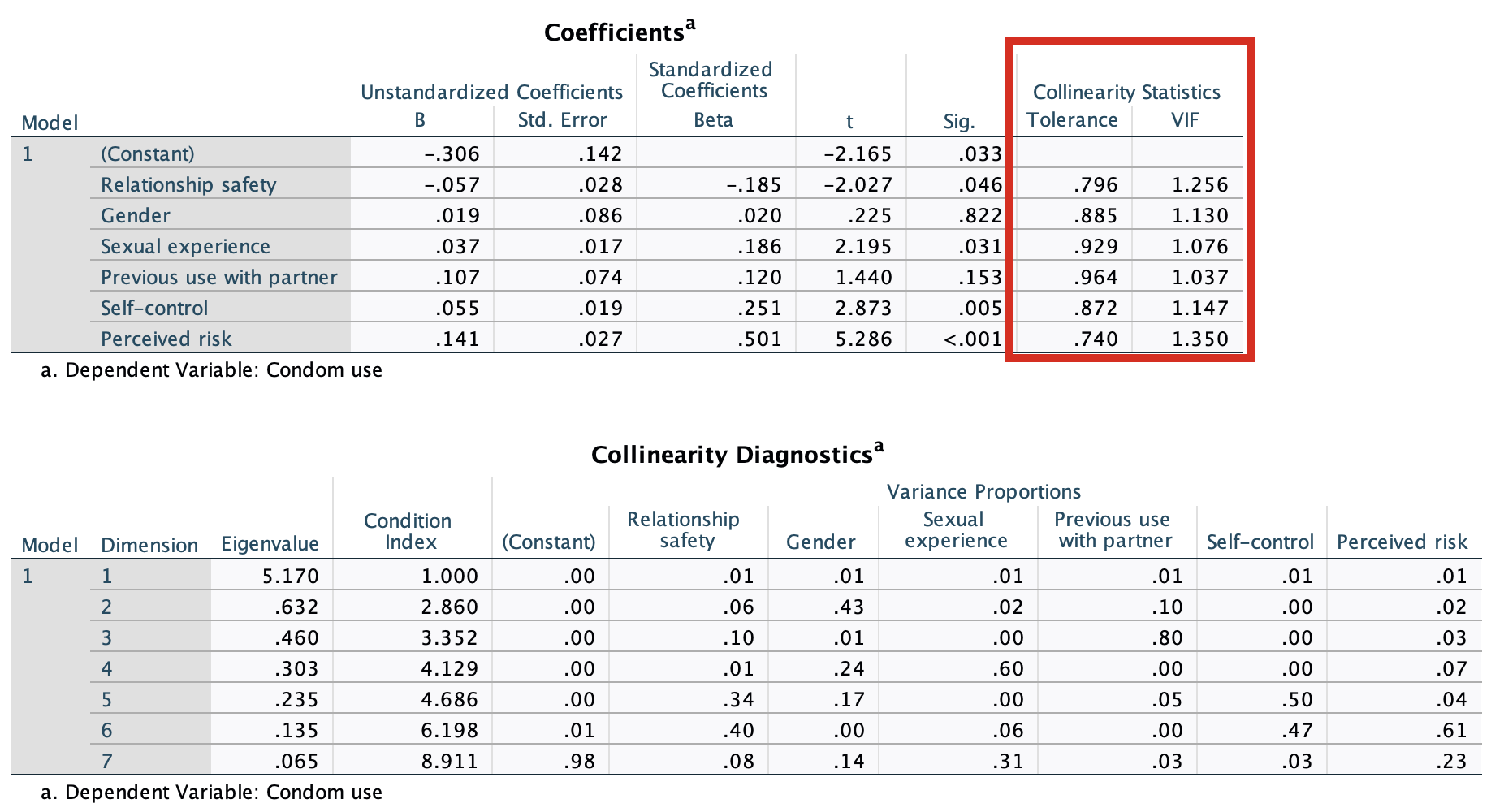
Residuals should be checked for influential cases and outliers. The output lists cases with standardized residuals greater than 2. In a sample of 100, we would expect around 5–10% of cases to have standardized residuals with absolute values greater than this value. For these data we have only four cases (out of 100) and only one of these has an absolute value greater than 3. Therefore, we can be fairly sure that there are no outliers (the number of cases with large standardized residuals is consistent with what we would expect).
Task 20.8
Using the final model from Task 6, what are the probabilities that participants 12, 53 and 75 will use a condom?
The values predicted for these cases will depend on exactly how you ran the analysis (and the parameter coding used on the variable previous). Therefore, your answers might differ slightly from mine.
Task 20.9
A female who used a condom in her previous encounter scores 2 on all variables except perceived risk (for which she scores 6). Use the model in Task 6 to estimate the probability that she will use a condom in her next encounter.
Use the logistic regression equation:
\[ p(Y_i) = \frac{1}{1 + e^{-Z}} \\ \] where
\[ Z = b_0 + b_1X_{1i} + b_2X_{2i} + ... + b_nX_{ni} \]
We need to use the values of b from the output (final model) and the values of X for each variable (from the question). The values of b we can get from an earlier output in Figure 486.
For the values of X, remember that we need to check how the categorical variables were coded. Again, refer back to an earlier output (Figure 482), but Figure 490 zooms in on the relevant part.

For example, a female is coded as 0, so that will be the value of X for this person. Similarly, she used a condom with her previous partner so this will be coded as 1 for previous(1) and 0 for previous(2).
The table below shows the values of b and X and then multiplies them.
| Predictor | b | X | bX |
|---|---|---|---|
| Perceived risk | 0.949 | 6 | 5.694 |
| Relationship safety | -0.482 | 2 | -0.964 |
| Biological sex | -0.003 | 0 | 0.000 |
| Previous use (1) | 1.087 | 1 | 1.087 |
| Previous use (2) | -0.017 | 0 | 0.000 |
| Self-control | 0.348 | 2 | 0.696 |
| Sexual experience | 0.180 | 2 | 0.360 |
| Constant | -4.957 | 1 | -4.957 |
We now sum the values in the last column to get the number in the brackets in the equation above:
\[ \begin{align} Z &= 5.694 -0.964 + 0.000 + 1.087 + 0.000 + 0.696 + 0.360 -4.957 \\ &= 1.916 \end{align} \]
Replace this value of z into the logistic regression equation:
\[ \begin{align} p(Y_i) &= \frac{1}{1 + e^{-Z}} \\ &= \frac{1}{1 + e^{-1.916}} \\ &= \frac{1}{1 + 0.147} \\ &= \frac{1}{1.147} \\ &= 0.872 \end{align} \]
Therefore, there is a 0.872 probability (87.2% if you prefer) that she will use a condom on her next encounter.
Task 20.10
At the start of the chapter we looked at whether the type of instrument a person plays is connected to their personality. A musicologist measured
extroversionand agreeableness in 200 singers and guitarists (instrument). Use logistic regression to see which personality variables (ignore their interaction) predict which instrument a person plays (sing_or_guitar.sav).
Follow the general instructions for logistic regression to fit the model. The main dialog box should look like Figure 491.
The first part of the output (Figure 492) tells us about the model when only the constant is included (i.e., all predictor variables are omitted). The log-likelihood of this baseline model is 271.957, which represents the fit of the model when including only the constant. At this point, the model predicts that every participant is a singer, because this results in more correct classifications than if the model predicted that everyone was a guitarist. Self-evidently, this model has 0% accuracy for the participants who played the guitar, and 100% accuracy for singers. Overall, the model correctly classifies 53.8% of participants.
The next part of the output summarizes the model, which at this stage tells us the value of the constant (\(b_0\)), which is −0.153. The table labelled Variables not in the Equation reports the residual chi-square statistic (labelled Overall Statistics) as 115.231 which is significant at p < .001 . This statistic tells us that the coefficients for the variables not in the model are significantly different from zero – in other words, the addition of one or more of these variables to the model will significantly improve predictions from the model. This table also lists both predictors with the corresonding value of Roa’s efficient score statistic ( labelled Score). Both excluded variables have significant score statistics at p < .001 and so both could potentially make a contribution to the model.
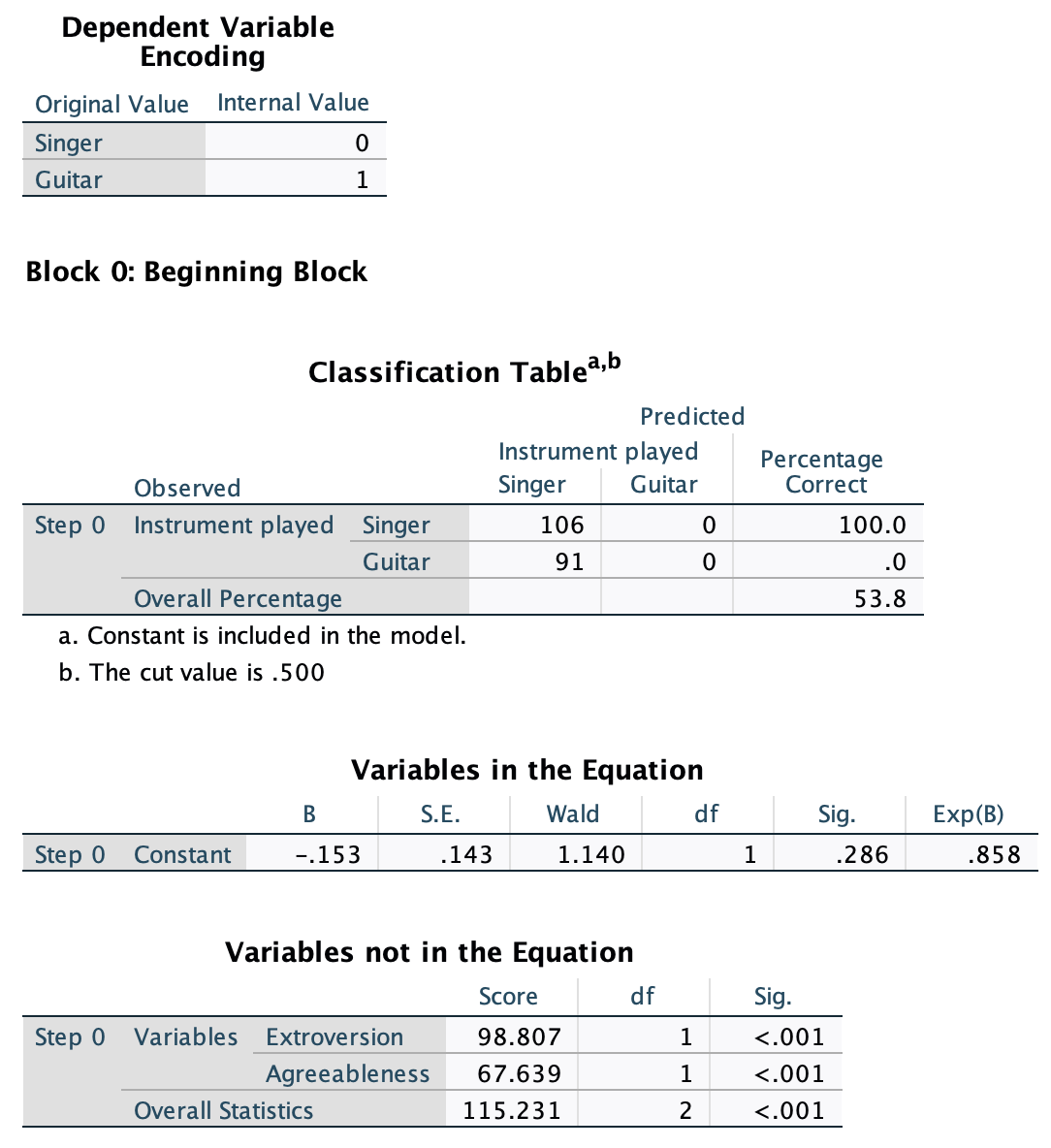
The next part of the output (Figure 493) deals with the model after these predictors have been added to the model. The overall fit of the new models is assessed using the −2log-likelihood statistic (−2LL). Remember that large values of the log-likelihood statistic indicate poorly fitting statistical models. The value of −2log-likelihood for a new model should, therefore, be smaller than the value for the previous model if the fit is improving. When only the constant was included, −2LL = 271.96, but with the two predictors added it has reduced to 225.18 (a change of 46.78), which tells us that the model is better at predicting which instrument participants’ played when both predictors are included.
The classification table how well the model predicts group membership. Before the predictors were entered into the model, the model correctly classified the 106 participants who are singers and misclassified all of the guitarests. So, overall it classified 53.8 of cases (see above). After the predictors are added it correctly classifies 103 of the 106 singers and 87 of the 91 guitarists. Overall then, it correctly classifies 96.4% of cases. A huge number (which you might want to think about for the following task!).
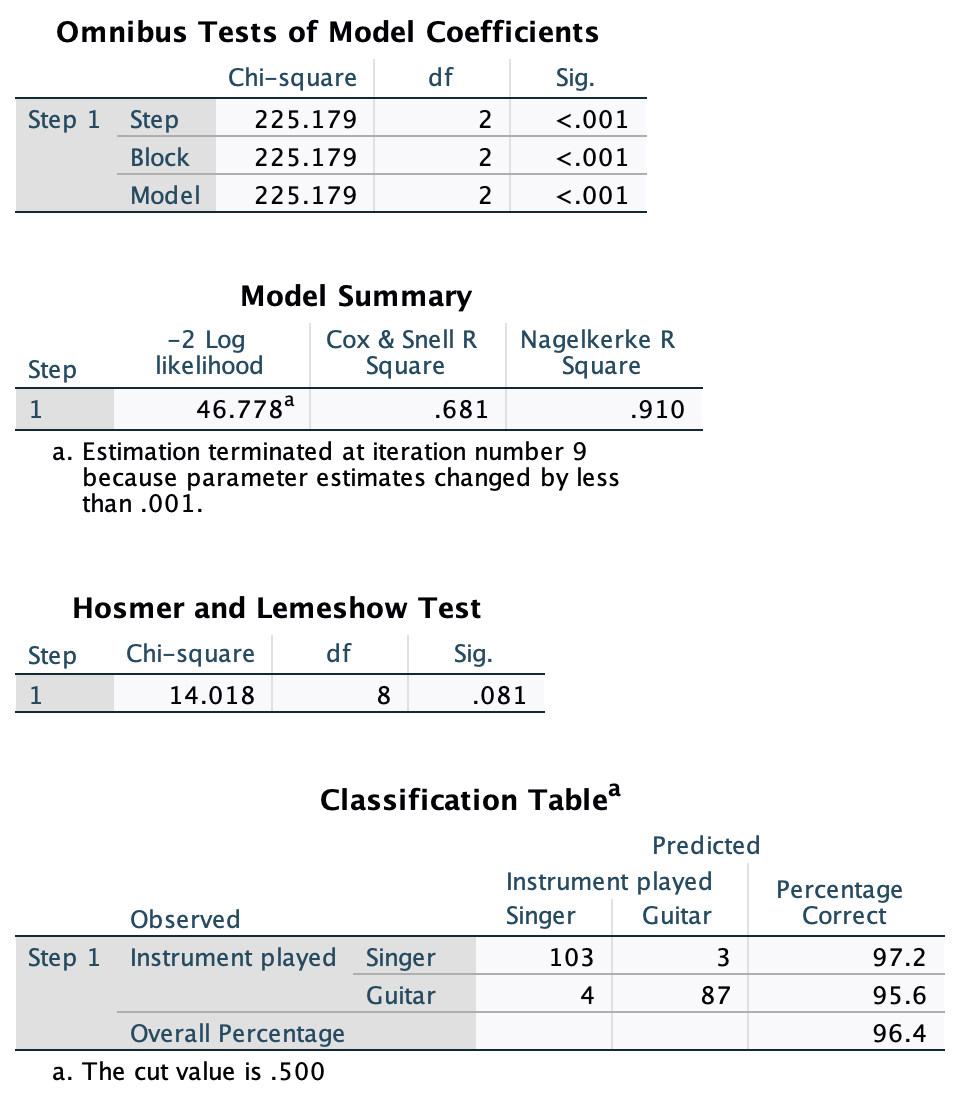
The table labelled Variables in the Equation (Figure 494) tells us the estimates for the coefficients for the predictors included in the model. These coefficients represents the change in the logit (log odds) of the outcome variable associated with a one-unit change in the predictor variable. The Wald statistics suggest that both extroversion, Wald(1) = 22.90, p < .001, and agreeableness, Wald(1) = 15.30, p < .001, significantly predict the instrument played. The corresponding odds ratio (labelled Exp(B)) tells us the change in odds associated with a unit change in the predictor. The odds ratio for extroversion is 0.238, which is less than 1 meaning that as the predictor (extroversion) increases, the odds of the outcome decrease, that is, the odds of being a guitarist (compared to a singer) decrease. In other words, more extroverted participants are more likely to be singers. The odds ratio for agreeableness is 1.429, which is greater than 1 meaning that as agreeableness increases, the odds of the outcome increase, that is, the odds of being a guitarist (compared to a singer) increase. In other words, more agreeable people are more likely to be guitarists. Note that the odds ratio for the constant is insanely large, which brings us neatly onto the next task …
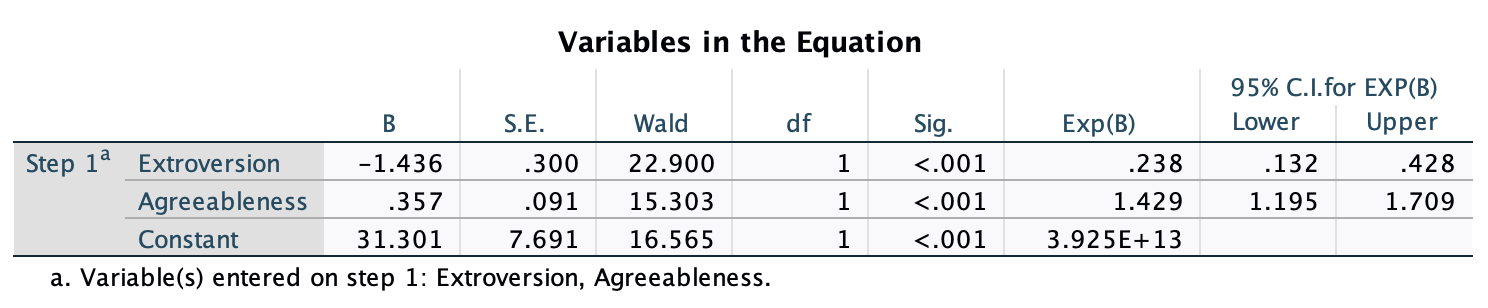
Task 20.11
Which problem associated with logistic regression might we have in the analysis in Task 10?
Looking at the classification plot, it looks as though we might have complete separation. The model almost perfectly predicts group membership.
Observed Groups and Predicted Probabilities
80 + +
IS I
IS I
F IS I
R 60 +S G+
E IS GI
Q IS GI
U IS GI
E 40 +S G+
N IS GI
C IS GI
Y IS GI
20 +S G+
IS GI
IS GI
ISSS S S S S S G G G G GGGGI
Predicted ---------+---------+---------+---------+---------+---------+---------+---------+---------+----------
Prob: 0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1
Group: SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG
Predicted Probability is of Membership for Guitar
The Cut Value is .50
Symbols: S - Singer
G - Guitar
Each Symbol Represents 5 Cases.Task 20.12
In a new study, the musicologist in Task 10 extended her previous one by collecting data from 430 musicians who played their voice (singers), guitar, bass, or drums (
instrument). She measured the same personality variables but also theirconscientiousness(band_personality.sav). Use multinomial logistic regression to see which of these three variables (ignore interactions) predict which instrument a person plays (use drums as the reference category).
I actually deleted this stuff from the book but forgot to delete this task. Oops. Oh well, here goes.
To fit the model select Analyze > Regression > Multinomial Logistic …. The main dialog box should look like the figure below. Drag the outcome instrument to the box labelled Dependent. We can specify which category to compare other categories against by clicking the Reference Category … button but the default is to use the last category, and this default is perfect for us because drums is the last category and is also the category that we want to use as our reference category.
Next, specify the predictor variables by dragging them (agreeableness, extroversion and conscientiousness) to the box labelled Covariate(s) (Figure 495). Click on and select the options in Figure 496 For a basic analysis in which all of these predictors are forced into the model, this is all we really need to do.
The first output (Figure 497) shows the log-likelihood. The change in log-likelihood indicates how much new variance has been explained by the model. The chi-square test tests the decrease in unexplained variance from the baseline model (1122.82) to the final model (450.91), which is a difference of 1149.53−871 = 672.02. This change is significant, which means that our final model explains a significant amount of the original variability in the instrument played (in other words, it’s a better fit than the original model).
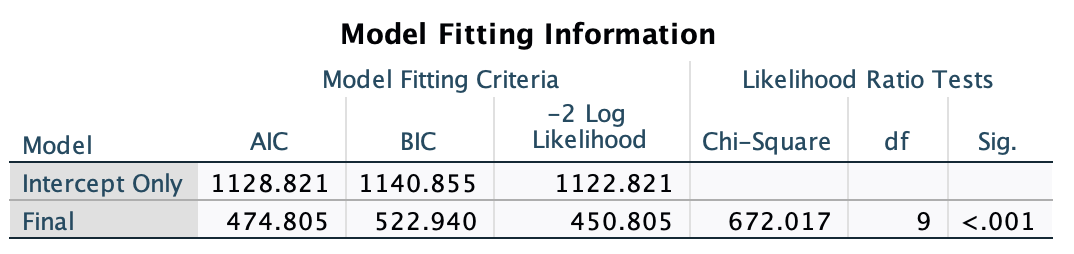
The next part of the output (Figure 498) relates to the fit of the model. We know that the model with predictors is significantly better than the one without predictors, but is it a good fit of the data? The Pearson and deviance statistics both test whether the predicted values from the model differ significantly from the observed values. If these statistics are not significant then the model is a good fit. Here we have contrasting results: the deviance statistic says that the model is a good fit of the data (p = 1.00, which is much higher than .05), but the Pearson test indicates the opposite, namely that predicted values are significantly different from the observed values (p < .001). Oh dear. Differences between these statistics can be caused by overdispersion. We can compute the dispersion parameters from both statistics:
\[ \begin{align} \phi_\text{Pearson} &= \frac{\chi_{\text{Pearson}}^2}{\text{df}} = \frac{1042672.72}{1140} = 914.63 \\ \phi_\text{Deviance} &= \frac{\chi_{\text{Deviance}}^2}{\text{df}} = \frac{448.032}{1140} = 0.39 \end{align} \]
The dispersion parameter based on the Pearson statistic is 914.63, which is ridiculously high compared to the value of 2, which I cited in the chapter as being a threshold for ‘problematic’. Conversely, the value based on the deviance statistic is below 1, which we saw in the chapter indicated underdispersion. Again, these values contradict, so all we can really be sure of is that there’s something pretty weird going on. Large dispersion parameters can occur for reasons other than overdispersion, for example omitted variables or interactions and predictors that violate the linearity of the logit assumption. In this example there were several interaction terms that we could have entered but chose not to, which might go some way to explaining these strange results.
The output also shows us the two other measures of \(R^2\). The first is Cox and Snell’s measure (.81) and the second is Nagelkerke’s adjusted value (.86). They are reasonably similar values and represent very large effects.
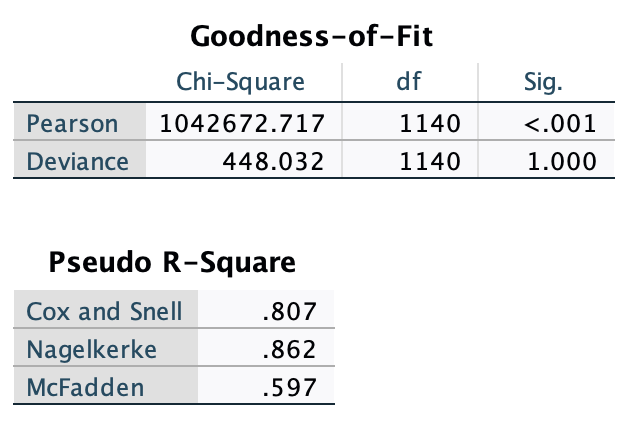
The likelihood ratio tests (Figure 499) can be used to ascertain the significance of predictors to the model. This table tells us that extroversion had a significant main effect on type of instrument played, \(\chi^2\)(3) = 339.73, p < .001, as did agreeableness, \(\chi^2\)(3) = 100.16, p < .001, and conscientiousness, \(\chi^2\)(3) = 84.26, p < .001.
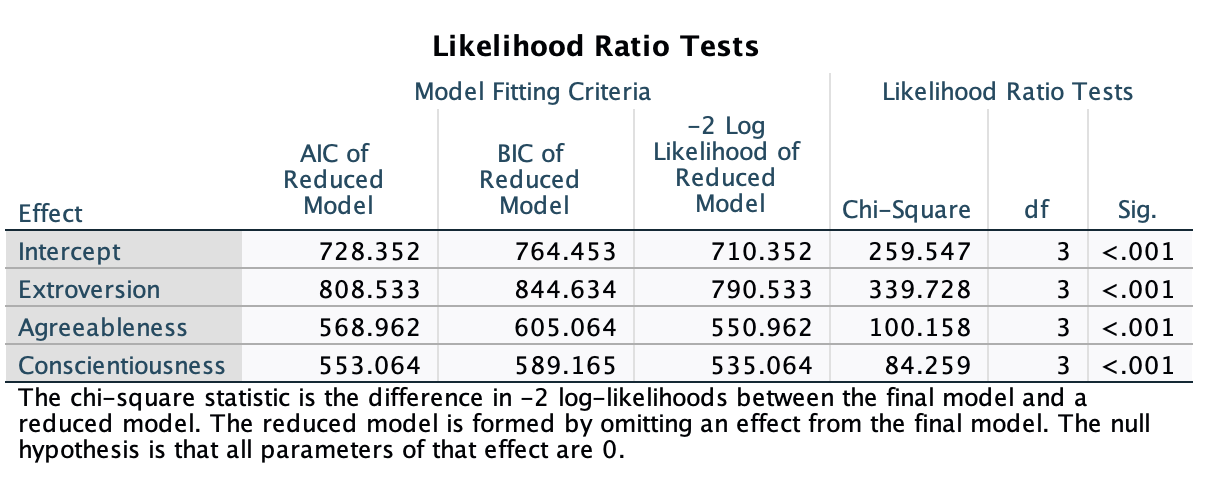
These likelihood statistics can be seen as overall statistics that tell us which predictors significantly enable us to predict the outcome category, but they don’t really tell us specifically what the effect is. To see this we have to look at the individual parameter estimates (Figure 500). We specified the last category (drums) as our reference category; therefore, each section of the table compares one of the instrument categories against the drums category. Let’s look at the effects one by one; because we are just comparing two categories the interpretation is the same as for binary logistic regression:
-
extroversion. Whether a person was a drummer or a singer was significantly predicted by how extroverted they were, b = 1.70, Wald \(\chi^2\)(1) = 54.34, p < .001. The odds ratio tells us that as extroversion increases by one unit, the change in the odds of being a singer (rather than being a drummer) is 5.47. The odds ratio (5.47) is greater than 1, therefore we can say that as participants move up the extroversion scale, they were more likely to be a singer (coded 1) than they were to be a drummer (coded 0). Similarly, Whether a person was a drummer or a bassist was significantly predicted by how extroverted they were, b = 0.25, Wald \(\chi^2\)(1) = 18.28, p < .001. The odds ratio tells us that as extroversion increases by one unit, the change in the odds of being a bass player (rather than being a drummer) is 1.29, so the more extroverted the participant was, the more likely they were to be a bass player than they were to be a drummer. However, whether a person was a drummer or a guitarest was not significantly predicted by how extroverted they were, b = .06, Wald \(\chi^2\)(1) = 3.58, p = .06. -
agreeableness. Whether a person was a drummer or a singer was significantly predicted by how agreeable they were, b = −0.40, Wald \(\chi^2\)(1) = 35.49, p < .001. The odds ratio tells us that as agreeableness increases by one unit, the change in the odds of being a singer (rather than being a drummer) is 0.67, so the more agreeable the participant was, the more likely they were to be a drummer than they were to be a singer. Similarly, whether a person was a drummer or a bassist was significantly predicted by how agreeable they were, b = −0.40, Wald \(\chi^2\)(1) = 41.55, p < .001. The odds ratio tells us that as agreeableness increases by one unit, the change in the odds of being a bass player (rather than being a drummer) is 0.67, so, the more agreeable the participant was, the more likely they were to be a drummer than they were to be a bass player. However, whether a person was a drummer or a guitarist was not significantly predicted by how agreeable they were, b = .02, Wald \(\chi^2\)(1) = 0.51, p = .48. -
conscientiousness. Whether a person was a drummer or a singer was significantly predicted by how conscientious they were, b = −0.35, Wald \(\chi^2\)(1) = 21.27, p < .001. The odds ratio tells us that as conscientiousness increases by one unit, the change in the odds of being a singer (rather than being a drummer) is 0.71, so the more conscientious the participant was, the more likely they were to be a drummer than they were to be a singer. Similarly, Whether a person was a drummer or a bassist was significantly predicted by how conscientious they were, b = −0.36, Wald \(\chi^2\)(1) = 40.93, p < .001. The odds ratio tells us that as conscientiousness increases by one unit, the change in the odds of being a bass player (rather than being a drummer) is 0.70, so the more conscientious the participant was, the more likely they were to be a drummer than they were to be a bass player. However, whether a person was a drummer or a guitarist was not significantly predicted by how conscientious they were, b = 0.00, Wald \(\chi^2\)(1) = 0.00, p = 1.00.
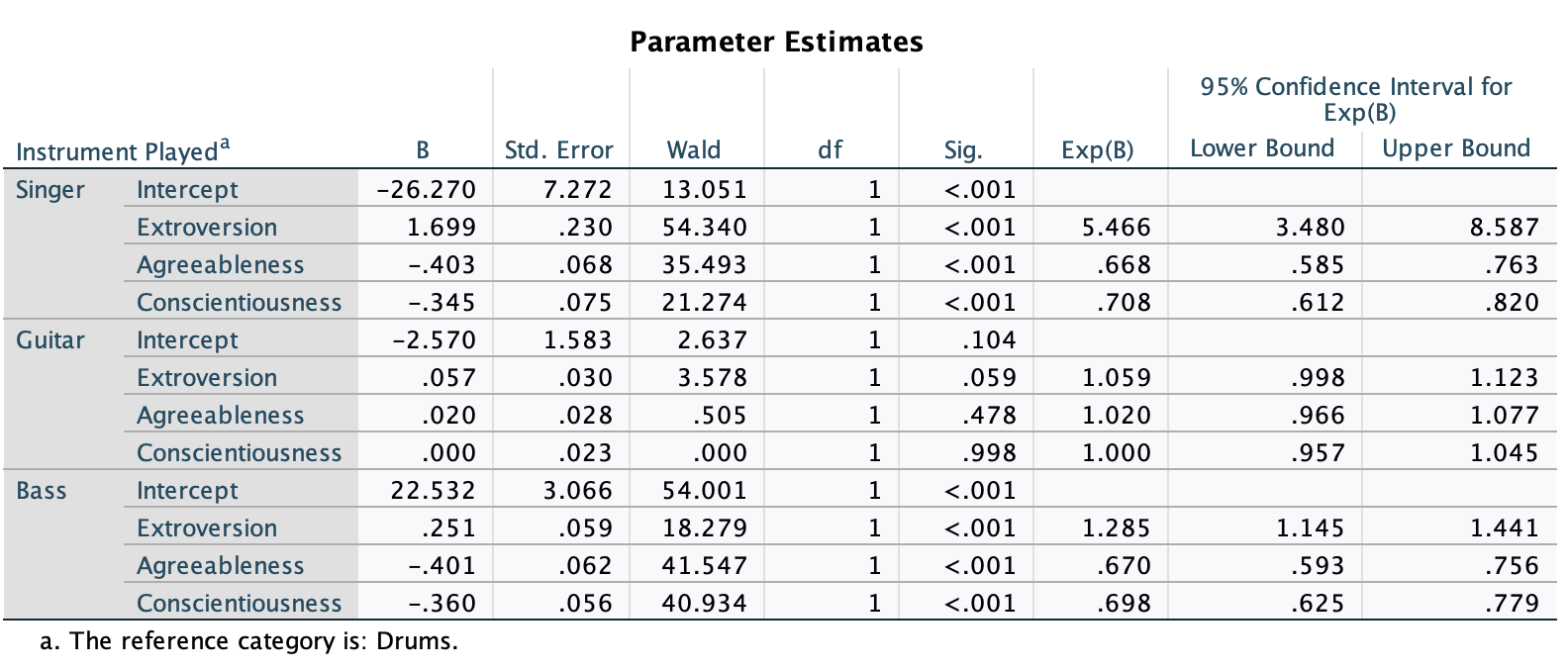
Chapter 21
Task 21.1
Using the cosmetic surgery example, run the analysis described in Section 21.5 but also including BDI as a fixed effect predictor. What differences does including this predictor make?
To fit the model follow the instructions in section 21.5 of the book except that the main dialog box (Figure 21.18 in the book) should include days, base_qoL, reason and bdi in the list of covariates: hold down Ctrl (⌘ on MacOS) to select all of these simultaneously and drag them to the box labelled Covariate(s):.
We’d set up the Fixed Effects dialog box as in Figure 504 (compare to Figure 21.19 in the book).
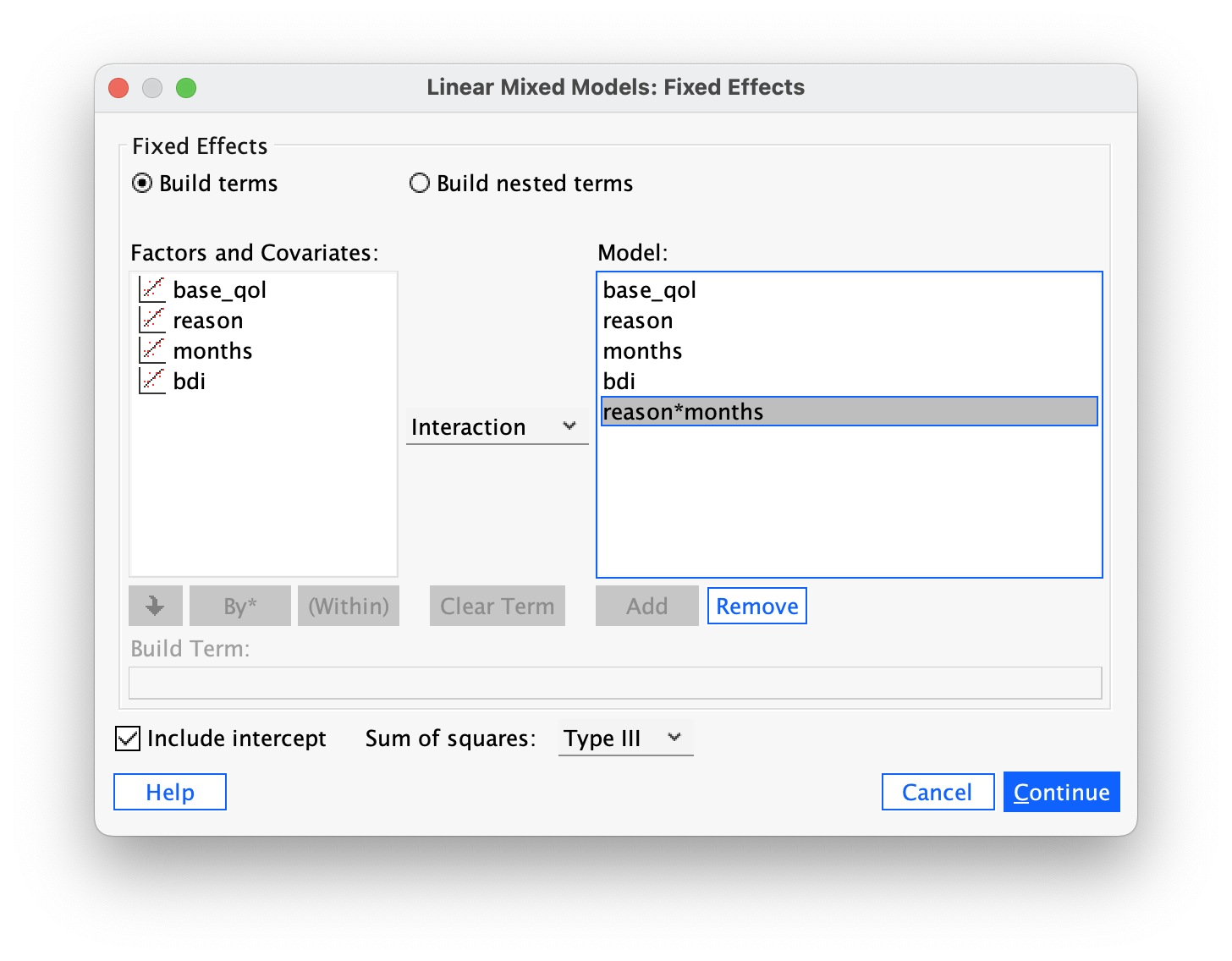
We’d set up the Random Effects dialog box Figure 504 (compare to Figure 21.20 in the book).
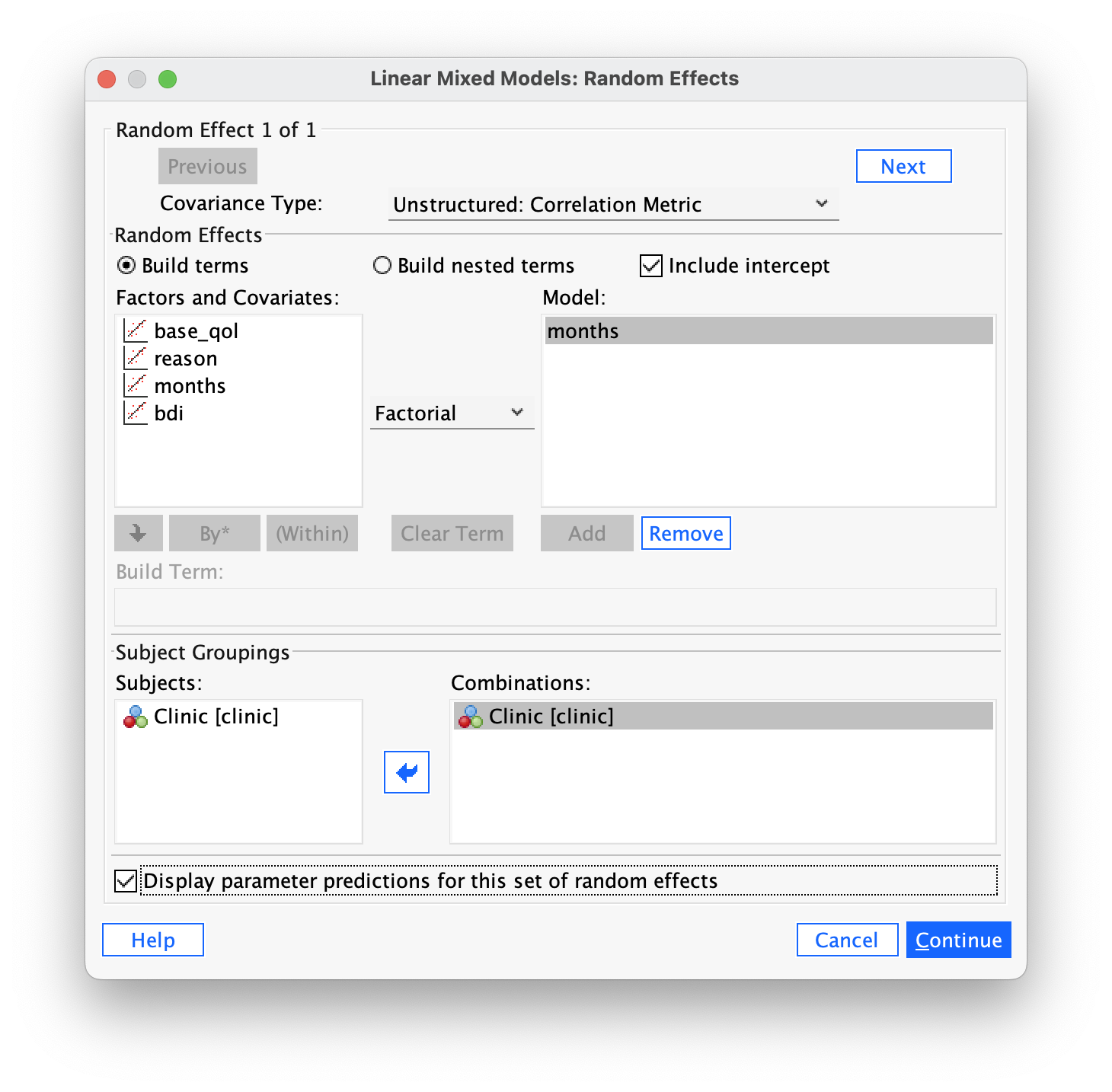
Set all of the other options as described for the example in the book. Your output should show the model set up as in Figure 506.
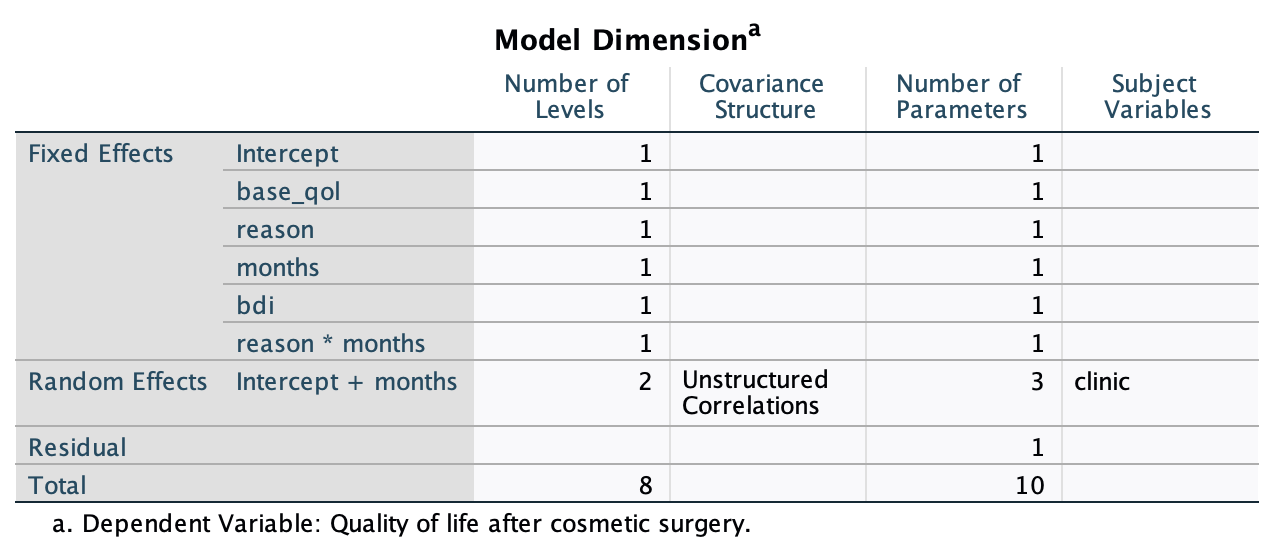
Looking at the fixed effects (Figure 507) bdi, F(1, 1533.18) = 56.36, p < .001, significantly predicted quality of life after surgery. Including bdi has not affected the interpretation of the other variables in the model. Obviously the parameter estimates themselves have changed (Figure 508), but how you’d interpret them is basically unchanged except that we’re now interpretting each one at fixed levels of depression.
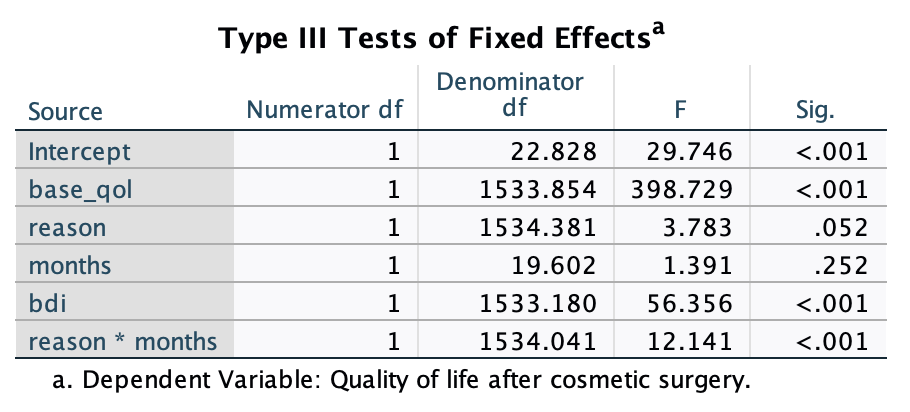
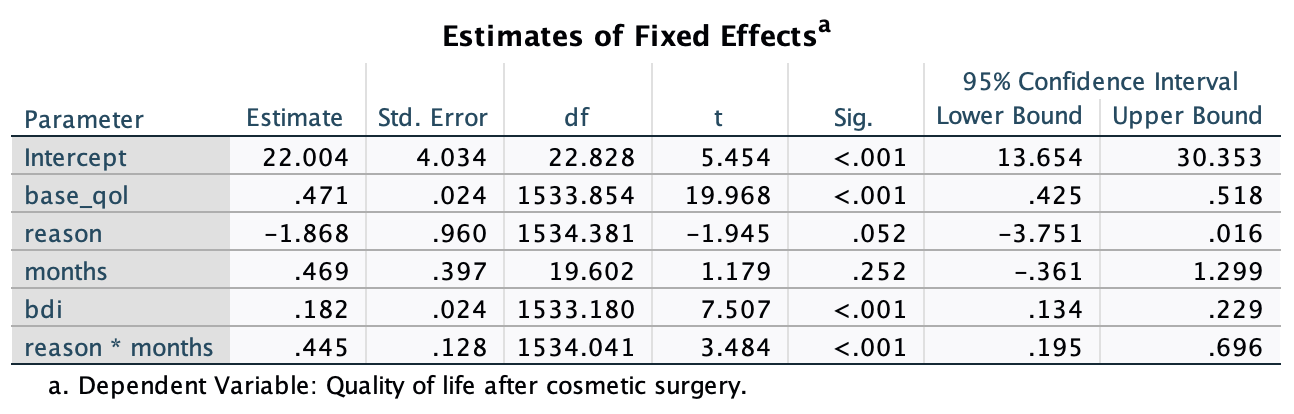
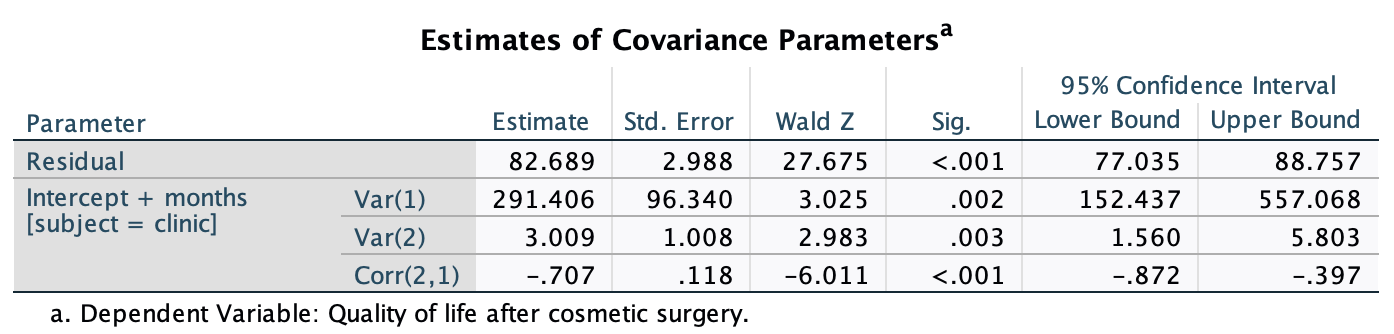
We could break down this interaction as we did in the chapter by splitting the file and running a simpler analysis (without th interaction and the main effect of reason, but including base_qoL, months, and bdi). If you do these analyses you will get the parameter tables in Figure 510. These tables show a similar pattern to the example in the book. For those operated on only to change their appearance, months did not significantly predict quality of life after surgery, b = 0.50, t(19.11) = 1.30, p = 0.208. However, for those who had surgery to help a physical problem, months did significantly predict quality of life, b = 0.90, t(18.74) = 2.11, p = 0.049. In essence, the inclusion of BDI has made very little difference.
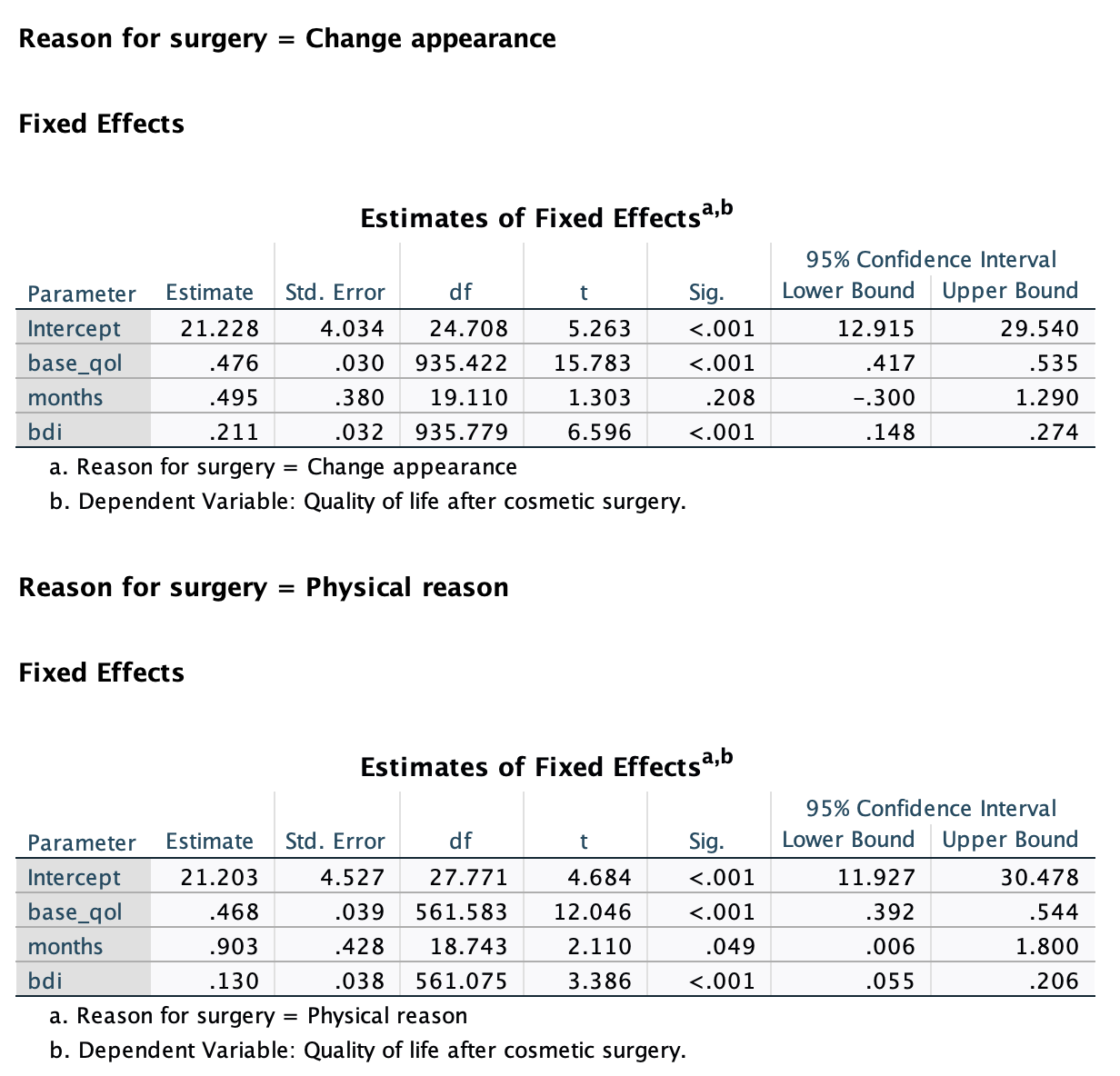
Task 21.2
Miller et al. (2007) tested the ‘hidden-estrus’ theory, which suggests that unlike other female mammals, humans do not experience an ‘estrus’ phase during which they are more sexually receptive, proceptive, selective and attractive. If this theory is wrong then human heterosexual men should find women most attractive during the fertile phase of their menstrual cycle compared to the pre-fertile (menstrual) and post-fertile (luteal) phase. Miller used the
tipsobtained by dancers (id) at a lap dancing club as a proxy for their sexual attractiveness and also recorded the phase of the dancer’s menstrual cycle during a given shift (cyclephase), and whether they were using hormonal contraceptives (contraceptive). Dancers provided data from between 9 and 29 of their shifts. Fit a multilevel model using these data (miller_2007.sav) to see whethertipscan be predicted fromcyclephase,contraceptiveand their interaction, allowing the overall level of tips to vary across dancers. Is the ‘hidden-estrus’ hypothesis supported?
Select Analyze > Mixed Models > Linear … to access the main dialog box. In this example, multiple scores or shifts are nested within each dancer. Therefore, the level 2 variable is the participant (the dancer) and this variable is represented by the variable labelled id. Drag this variable to the box labelled Subjects and click  to access the main dialog box (Figure 511).
to access the main dialog box (Figure 511).
In the main dialog box we need to set up our predictors and outcome. The outcome was the value of tips earned, so drag tips to the box labelled Dependent variable:. We have two predictors: cyclephase and contraceptive. Drag both of these to the box labelled Factor(s):. We use the Factor(s) box because both variables are categorical (Figure 512).
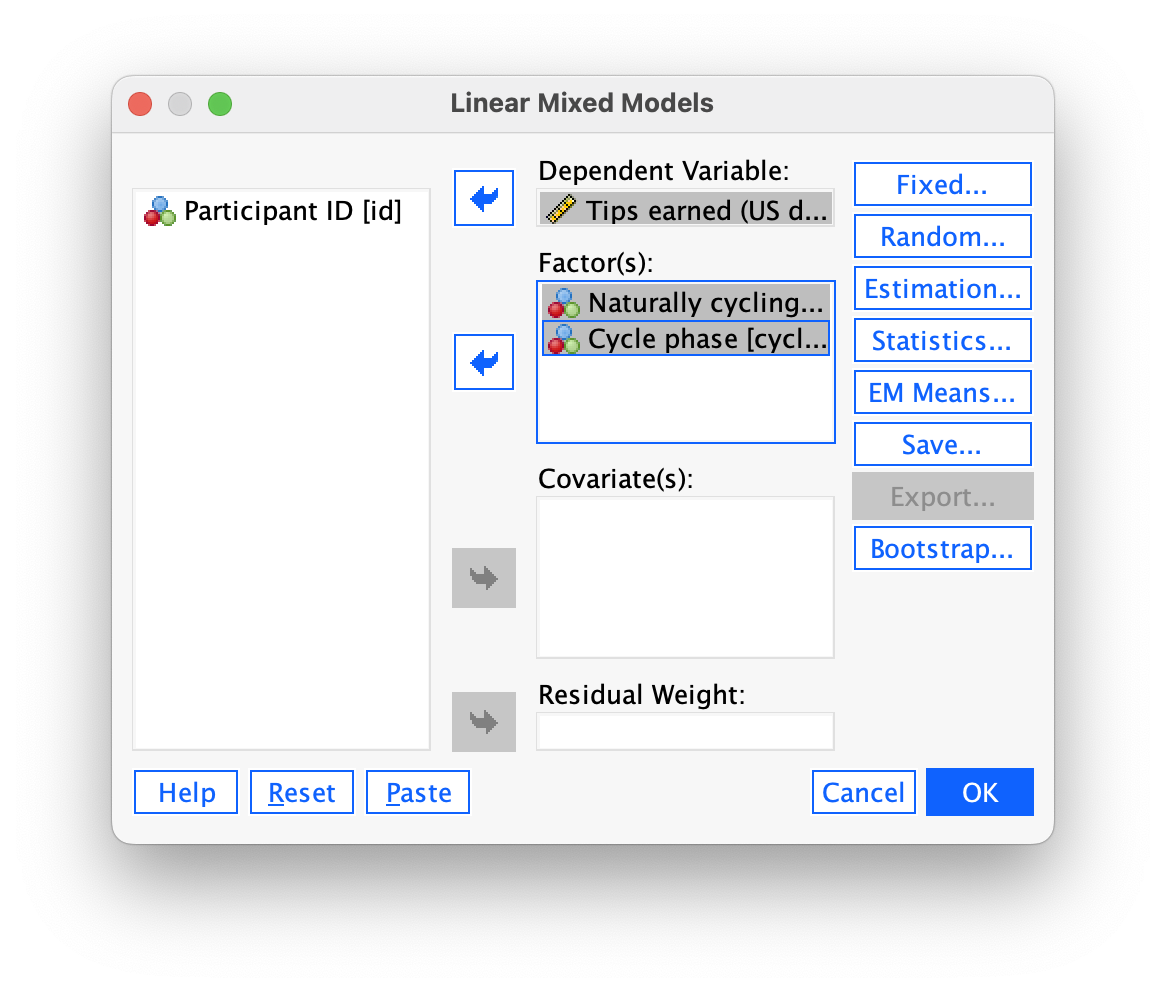
To add these fixed effects to our model click on  to access the Fixed Effects dialog box (Figure 513). To specify both main effects and the interaction term, select both predictors (click on
to access the Fixed Effects dialog box (Figure 513). To specify both main effects and the interaction term, select both predictors (click on cyclephase and then, while holding down Ctrl (⌘ on a mac), click on contraceptive), then select  , and then click
, and then click  . You should find that both main effects and the interaction term are transferred to the Model: box. Click
. You should find that both main effects and the interaction term are transferred to the Model: box. Click  to return to the main dialog box.
to return to the main dialog box.
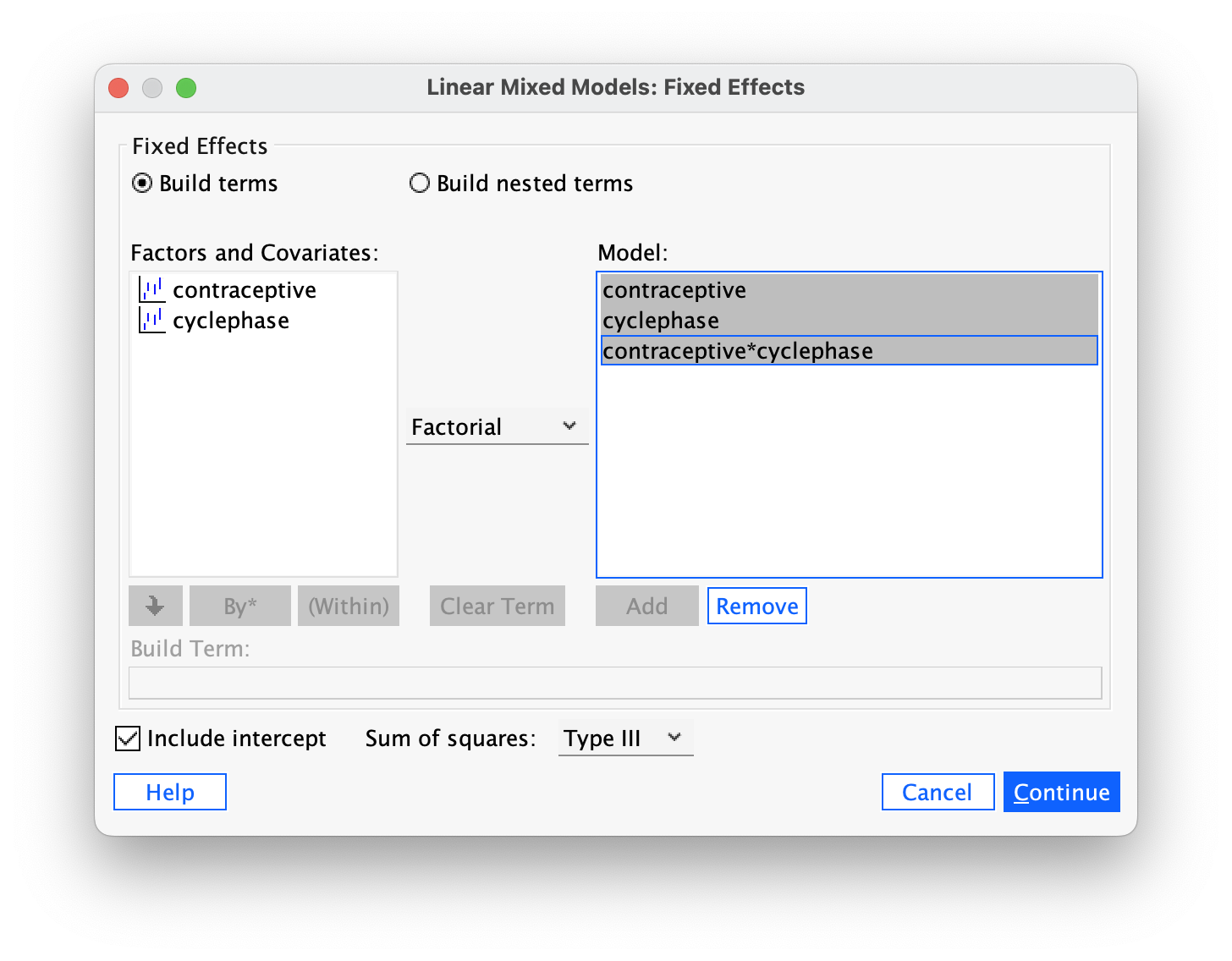
In the model that Miller et al. fitted, they did not assume that there would be random slopes (i.e., the relationship between each predictor and tips was not assumed to vary within lap dancers). This decision is appropriate for contraceptive because this variable didn’t vary at level 2 (the lap dancer was either taking contraceptives or not, so this could not be set up as a random effect because it doesn’t vary over our level 2 variable of participant). Also, because cyclephase is a categorical variable with three unordered categories we could not expect a linear relationship with tips: we expect tips to vary over categories but the categories themselves have no meaningful order. However, we might expect tips to vary over participants (some lap dancers will naturally get more money than others) and we can factor this variability in by allowing the intercept to be random. As such, we’re fitting a random intercept model to the data.
To do this, click on  in the main dialog box to access the Random Effects dialog box (Figure 514). The first thing we need to do is to specify our contextual variable. We do this by selecting it from the list of contextual variables that we have already specified. These appear in the section labelled Subjects. Because we specified only one variable, there is only one variable in the list,
in the main dialog box to access the Random Effects dialog box (Figure 514). The first thing we need to do is to specify our contextual variable. We do this by selecting it from the list of contextual variables that we have already specified. These appear in the section labelled Subjects. Because we specified only one variable, there is only one variable in the list, id.
Drag this variable to the area labelled Combinations. We want to specify that only the intercept is random, and we do this by selecting  . Notice that this dialog box includes a drop-down list used to specify the type of covariance (
. Notice that this dialog box includes a drop-down list used to specify the type of covariance ( ). For a random intercept model this default option is fine. Click
). For a random intercept model this default option is fine. Click  to return to the main dialog box.
to return to the main dialog box.
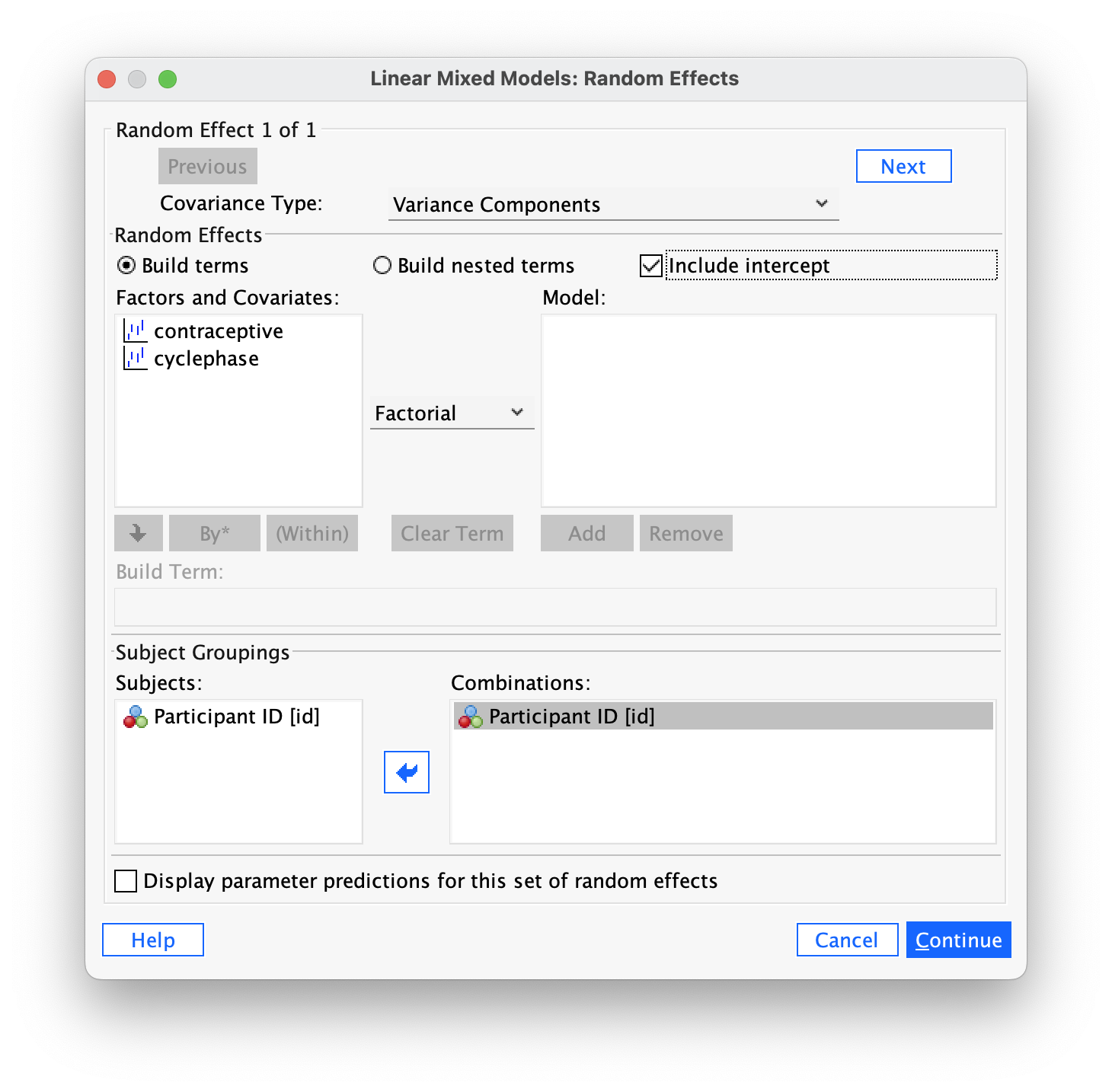
The authors report in the paper that they used restricted maximum-likelihood estimation (REML), so click on  and select this option. Finally, click
and select this option. Finally, click  and select Parameter estimates and Tests for covariance parameters. Click
and select Parameter estimates and Tests for covariance parameters. Click  to return to the main dialog box. To fit the model click
to return to the main dialog box. To fit the model click  .
.
The first output tells us our fixed effects. As you can see they are all significant (Figure 515).
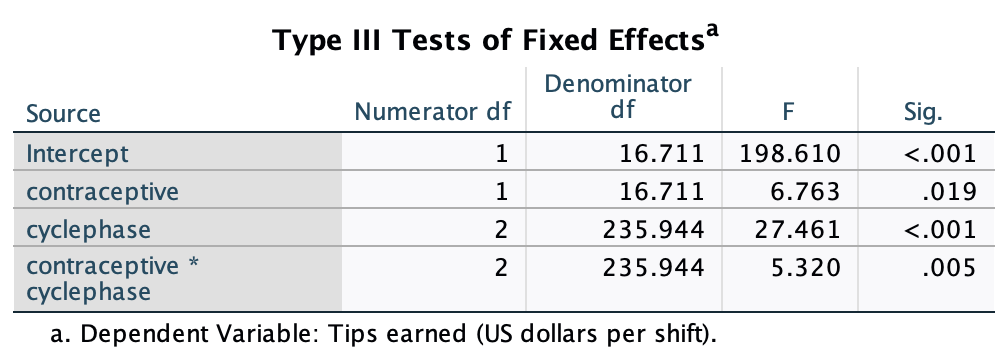
Basically the results show that the phase of the dancer’s cycle significantly predicted tip income, and this interacted with whether or not the dancer was having natural cycles or was on the contraceptive pill. However, we don’t know which groups differed. We can use the parameter estimates to tell us.
I coded cyclephase in a way that would be most useful for interpretation, which was to code the group of interest (fertile period) as the last category (3), and the other phases as 2 (Luteal) and 1 (Menstrual). The parameter estimates for this variable, therefore, compare each category against the last category, and because I made the last category the fertile phase this means we get a comparison of the fertile phase against the other two. We need to focus on the contrasts for the interaction term. The first of these tells us the following: if we worked out the relative difference in tips between the fertile phase and the menstrual phase, how much more do those in their natural cycle earn compared to those on contraceptive pills? The answer is about –$90. In other words, there is a combined effect of being on the pill (relative to in a natural cycle) and being in the fertile phase (relative to the Menstrual phase), and this is significant, \(\hat{b}\) = –89.94, t(236.81) = –2.63, p = .009. The second contrast tells us the following: if we worked out the relative difference in tips between the fertile phase and the Luteal phase, how much more do those on contraceptive pill earn compared to those in their natural cycle? The answer is about –$86 (the \(\hat{b}\)). In other words, there is a combined effect of being in a natural cycle and being in the fertile phase compared to the menstrual phase, and this is significant, \(\hat{b}\) = 86.09, t(237) = –2.87, p = .005.
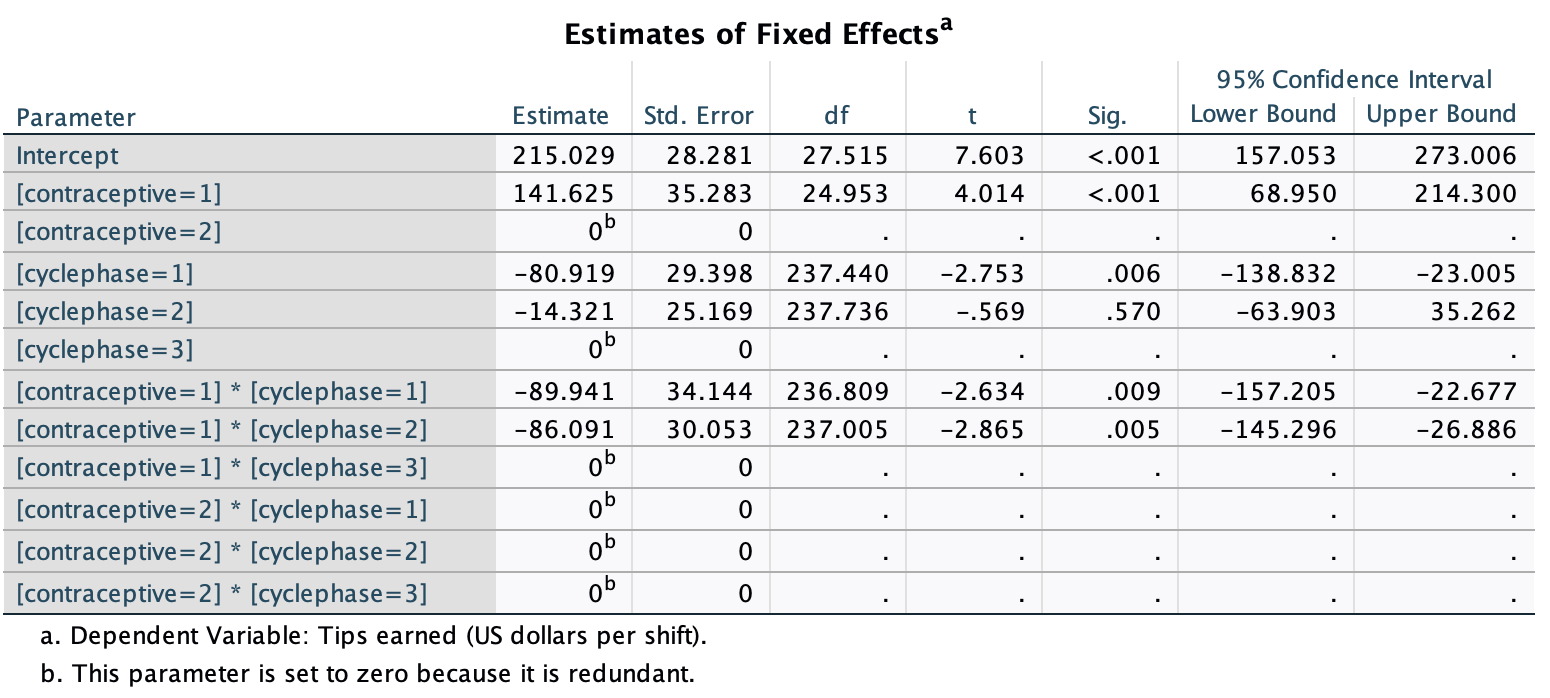
The final table (Figure 517) is not central to the hypotheses, but it does tell us about the random intercept. In other words, it tells us whether tips (in general) varied from dancer to dancer. The variance in tips across dancers was 3566.38, and this is significant, z = 2.37, p = .018. In other words, the average tip per dancer varied significantly. This confirms that we were justified in treating the intercept as a random variable.

To conclude, then, this study showed that the ‘estrus-hidden’ hypothesis is wrong: men did find women more attractive (as indexed by how many lap dances a woman performed and therefore how much she earned) during the fertile phase of their cycle compared to the other phases.
Task 21.3
Hill et al. (2007) examined whether providing children with a leaflet based on the ‘theory of planned behaviour’ increased their exercise. There were four different interventions (
intervention): a control group, a leaflet, a leaflet and quiz, and a leaflet and a plan. A total of 503 children from 22 different classrooms were sampled (classroom). The 22 classrooms were randomly assigned to the four different conditions. Children were asked ‘On average over the last three weeks, I have exercised energetically for at least 30 minutes ______ times per week’ after the intervention (post_exercise). Run a multilevel model analysis on these data (hill_2007.sav) to see whether the intervention affected the children’s exercise levels (the hierarchy is children within classrooms within interventions).
To fit the model use the Analyze > Mixed Models > Linear … menu to access the first dialog box, which should be completed as in Figure 518.
Click  to access the main dialog box and complete it as in Figure 519.
to access the main dialog box and complete it as in Figure 519.
The Fixed Effects dialog box should look like Figure 520.
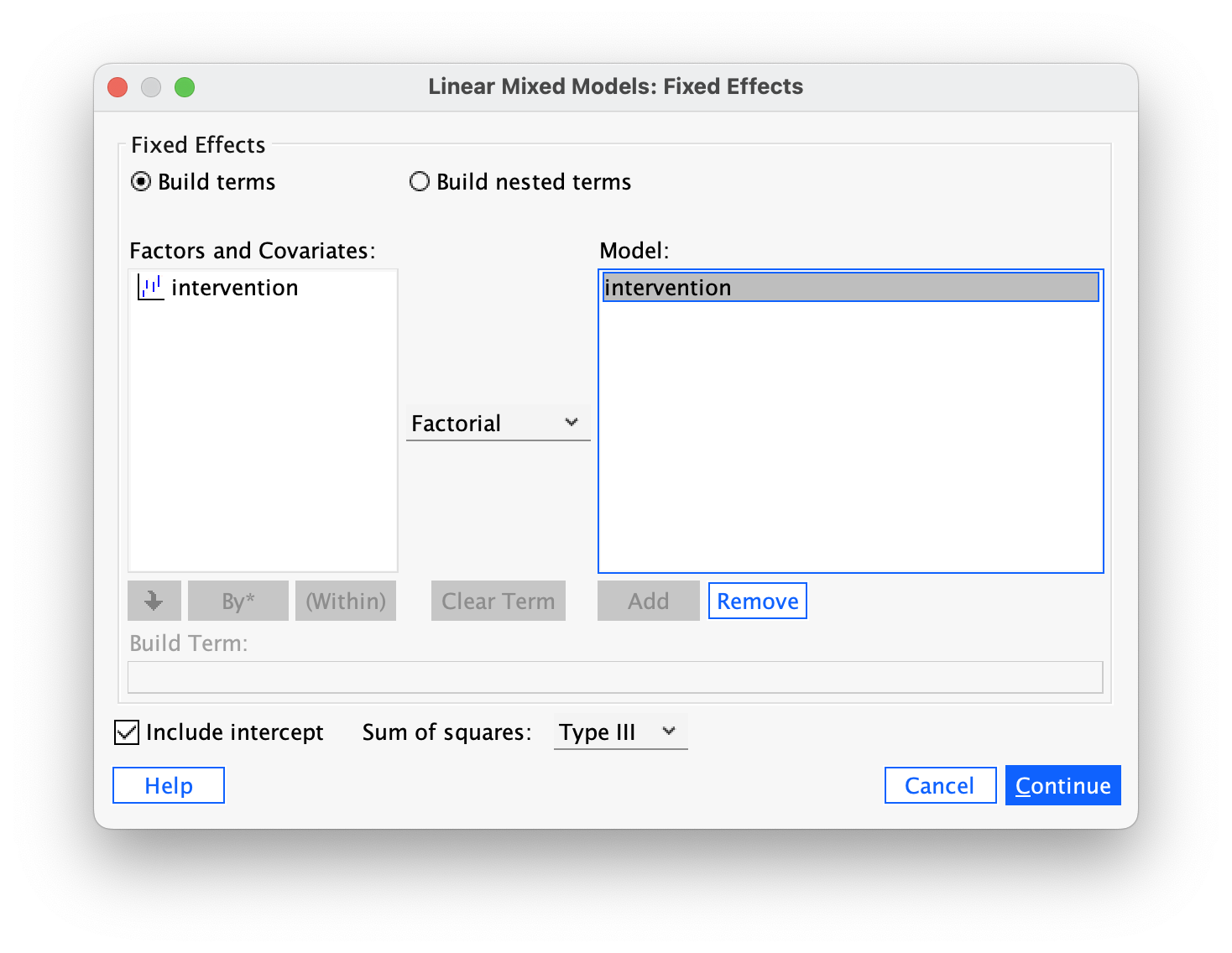
The Random Effects dialog box should look like Figure 521.
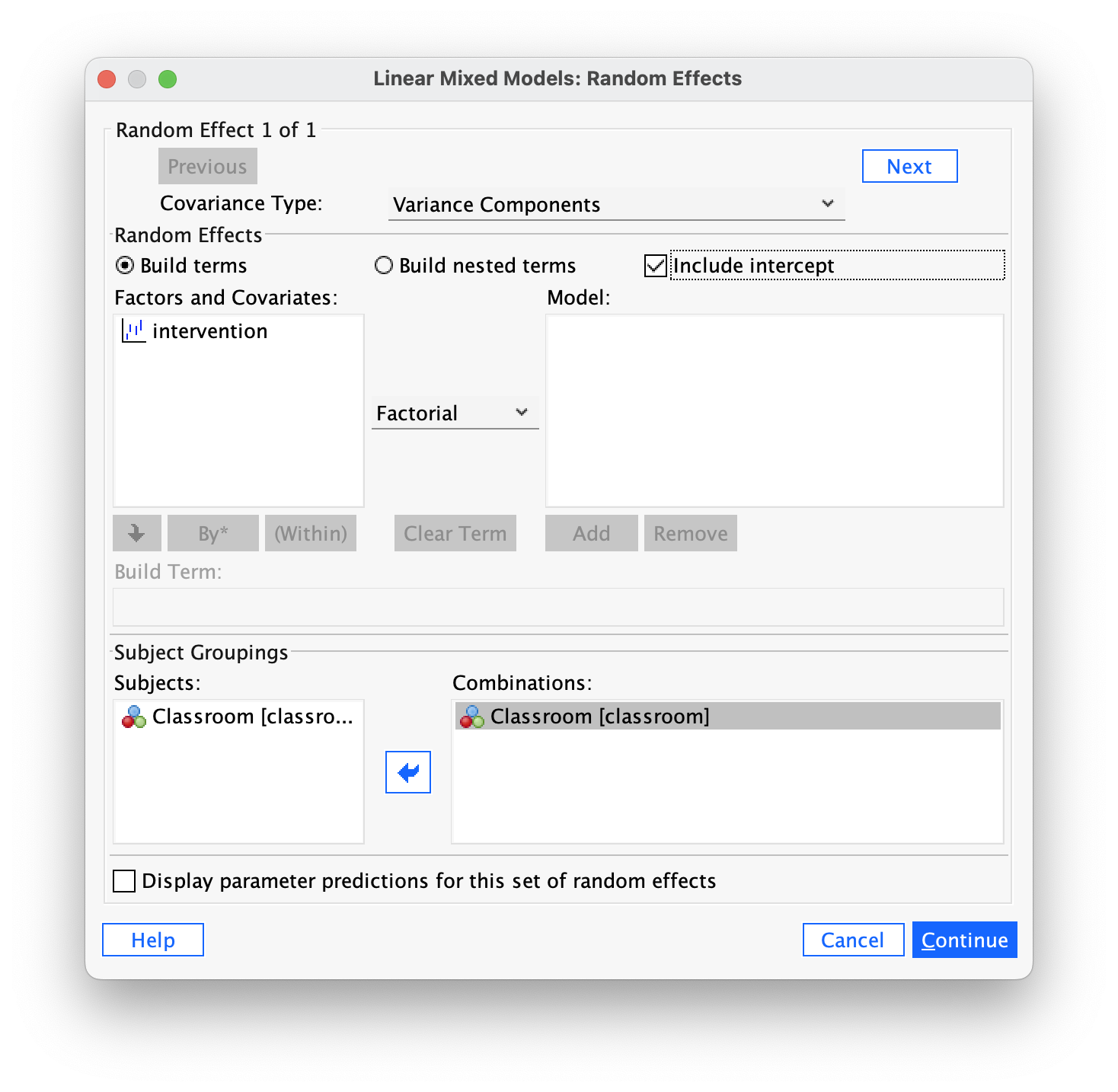
The Estimation dialog box should look like Figure 522 and the Statistics dialog box should look like Figure 502.
The first part of the output (Figure 523) tells you details about the model that are being entered into the SPSS machinery. The Information Criteria table gives some of the popular methods for assessing the fit models. AIC and BIC are two of the most popular.
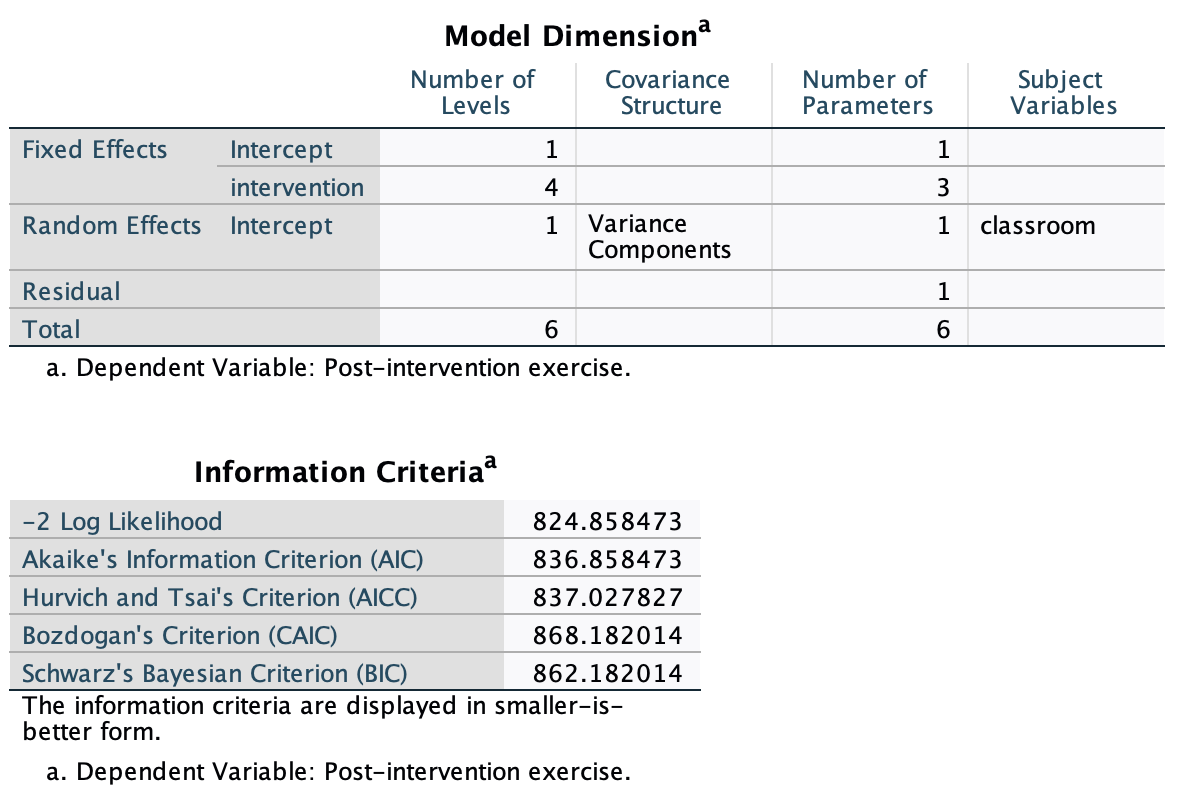
The Fixed Effects (Figure 524) gives the information in which most of you will be most interested. It says the effect of intervention is non-significant, F(3, 22.10) = 2.08, p = .132. A few words of warning: calculating a p-value requires assuming that the null hypothesis is true. In most of the statistical procedures covered in this book you would construct a probability distribution based on this null hypothesis, and often it is fairly simple, like the z- or t-distributions. For multilevel models the probability distribution of the null is often not known. Most packages that estimate p-values for multilevel models estimate this probability in complex way. This is why the denominator degrees of freedom are not whole numbers. For more complex models there is concern about the accuracy of some of these approximations. Many methodologists urge caution in rejecting hypotheses even when the observed p-value is less than .05.
The random effects (Figure 525) show how much of the variability in responses is associated with which class a person is in: 0.017178/(0.017178 + 0.290745) = 5.58%. This is fairly small. The corresponding Wald z just fails to reach the traditional level for statistical significance, p = .057. The result from these data could be that the intervention failed to affect exercise. However, there is a lot of individual variability in the amount of exercise people get. A better approach would be to take into account the amount of self-reported exercise prior to the study as a covariate, which leads us to the next task.
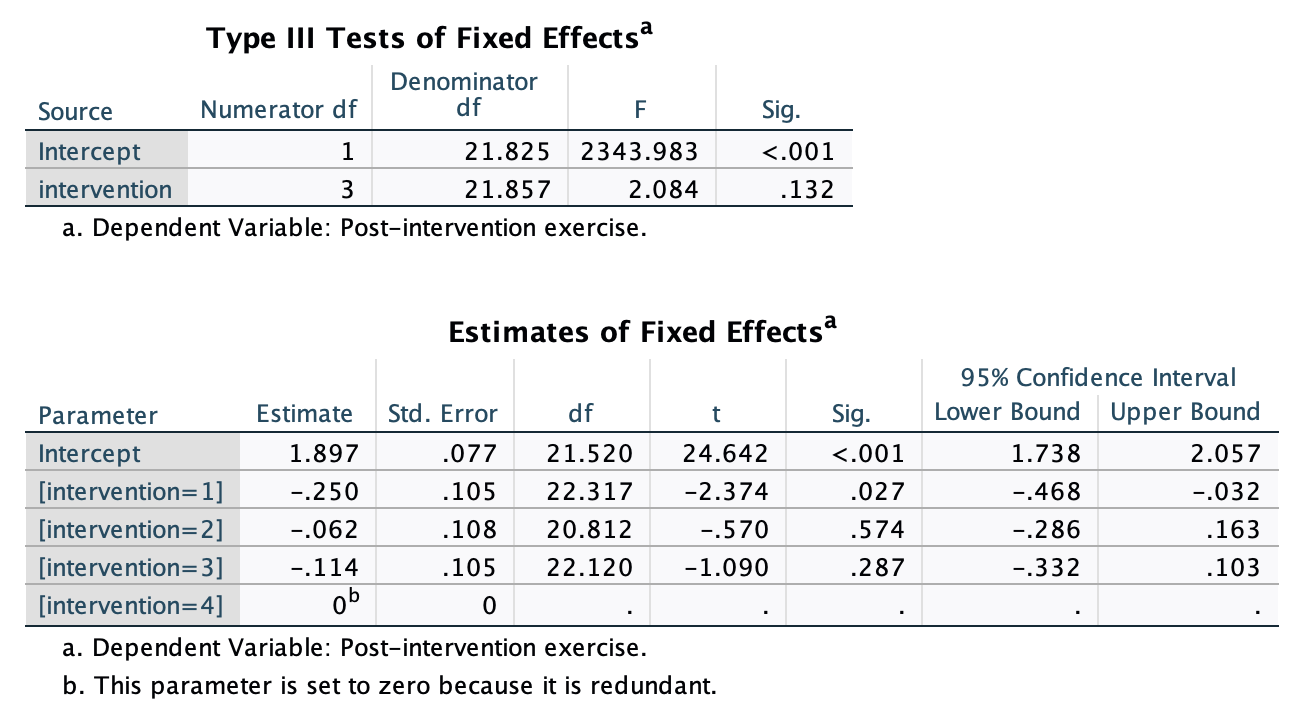
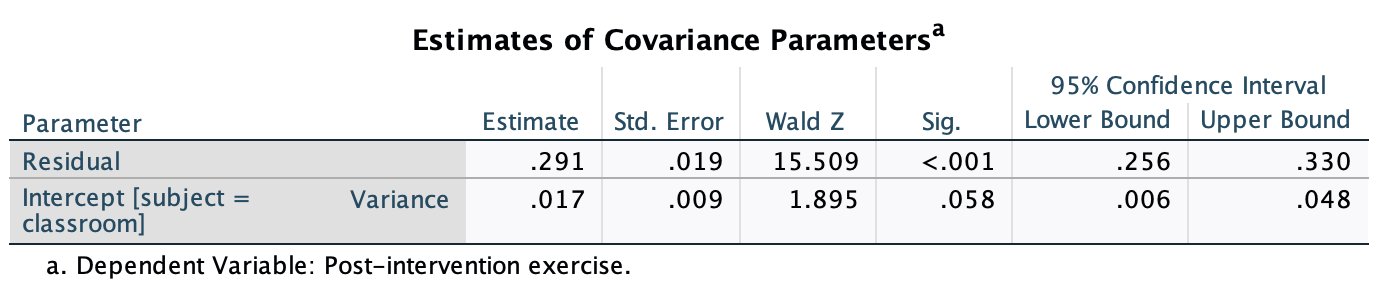
Task 21.4
Repeat the analysis in Task 3 but include the pre-intervention exercise scores (pre_exercise) as a covariate. What difference does this make to the results?
To fit the model follow the instructions for the previous task excpe the main dialog box should be completed as in (Figure 526).
and the Fixed Effects dialog box should look like (Figure 527).
Otherwise complete the dialog boxes in the same way as the previous example. The first part of the output (Figure 528) tells you details about the model that is being entered into the SPSS machinery. The Information Criteria box gives some of the popular methods for assessing the fit models. AIC and BIC are two of the most popular.
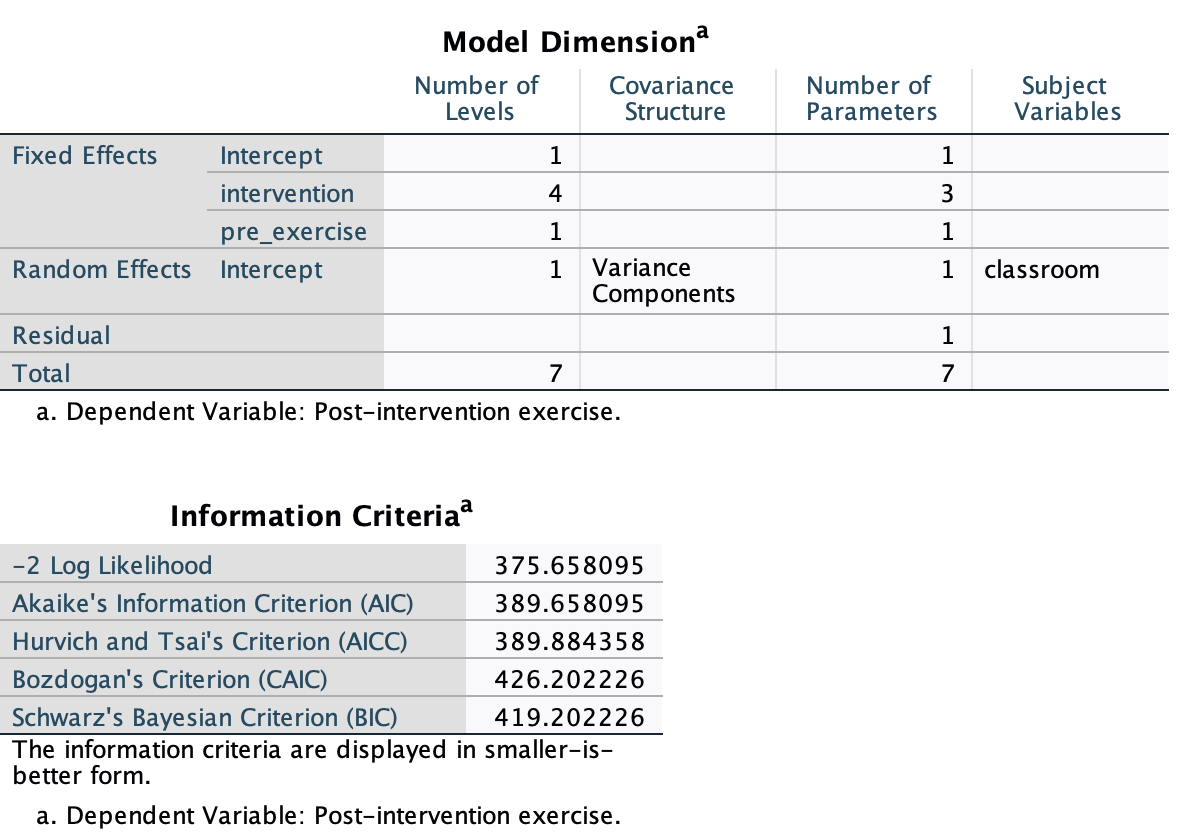
The Fixed Effects (Figure 529) gives the information in which most of you will be most interested. It says the effect of pre-intervention exercise level is a significant predictor of post-intervention exercise level, F(1, 478.54) = 719.775, p < .001, and, most interestingly, the effect of intervention is now significant, F(1, 22.83) = 8.02, p = .001. These results show that when we adjust for the amount of self-reported exercise prior to the study, the intervention group becomes a significant predictor of post-intervention exercise levels.
The random effects (Figure 530) show how much of the variability in responses is associated with which class a person is in: 0.001739/(0.001739 + 0.122045) = 1.40%. This is pretty small. The corresponding Wald z is not significant, p = .410.
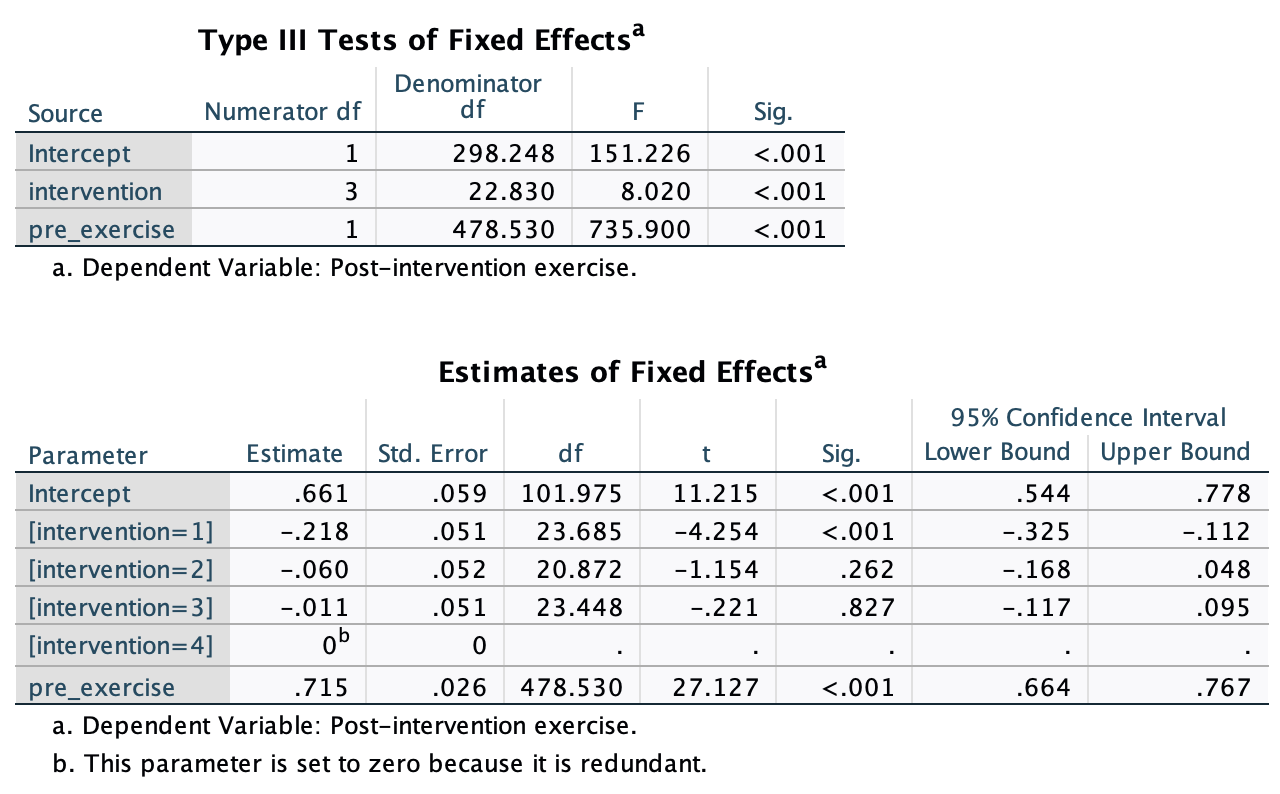
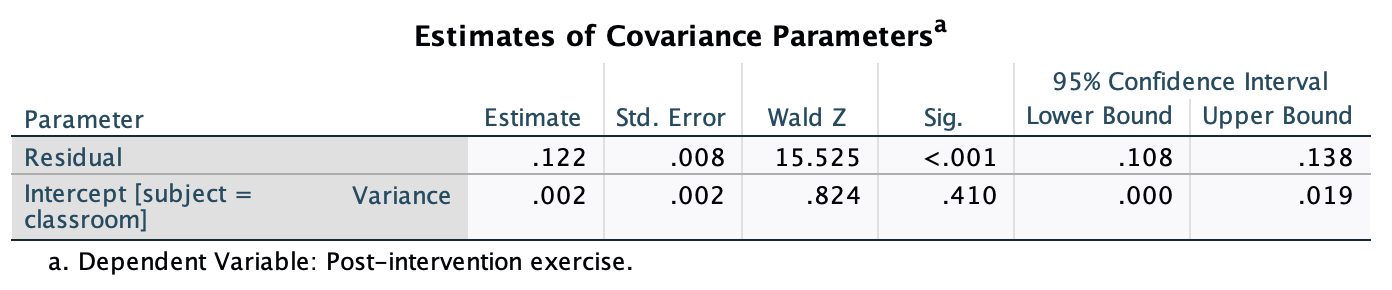
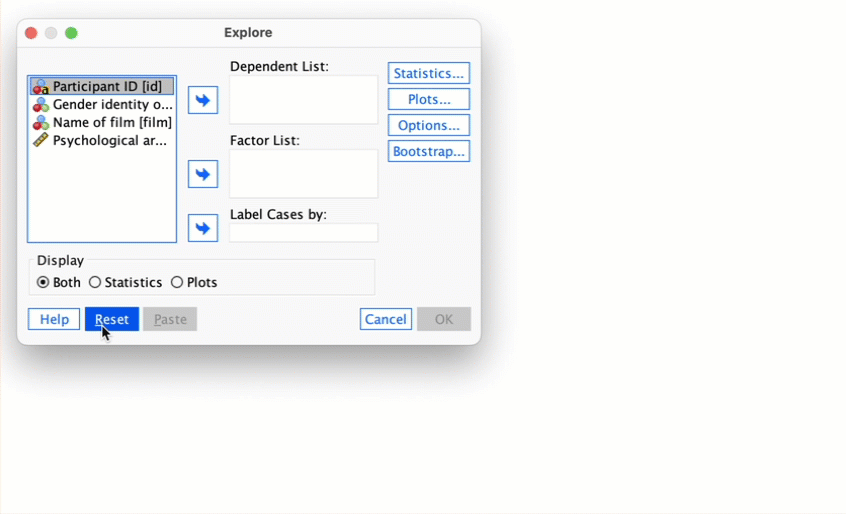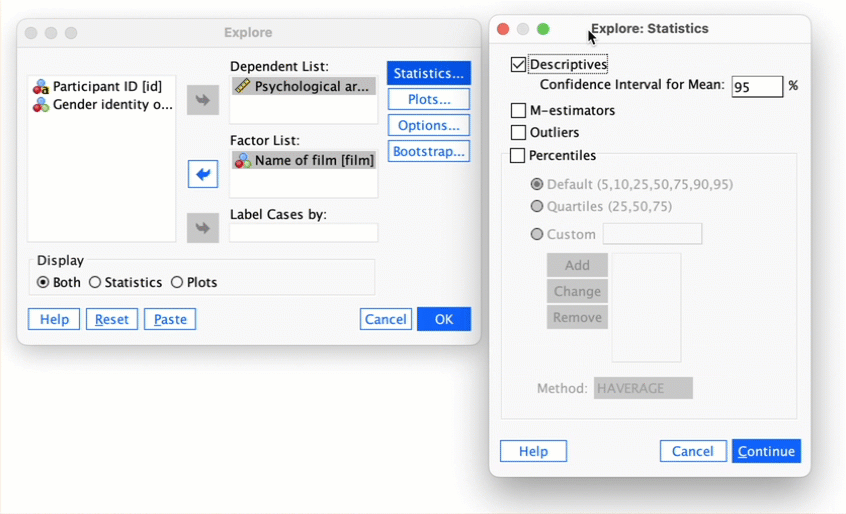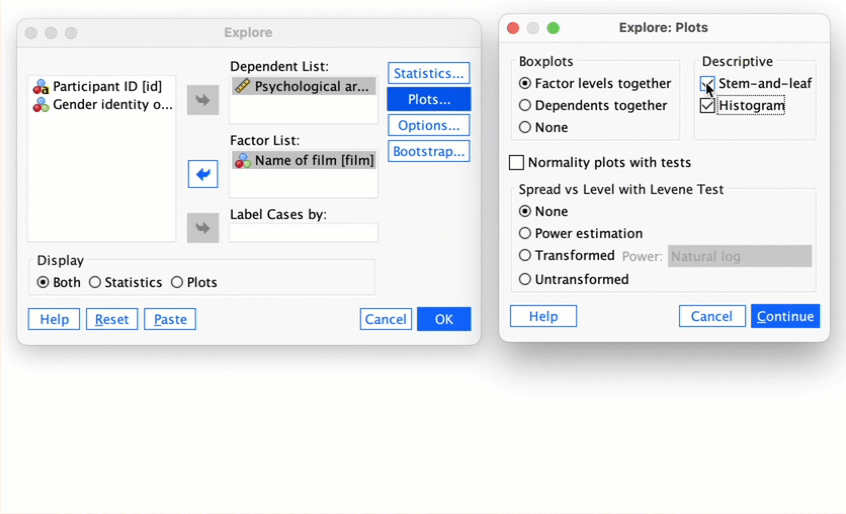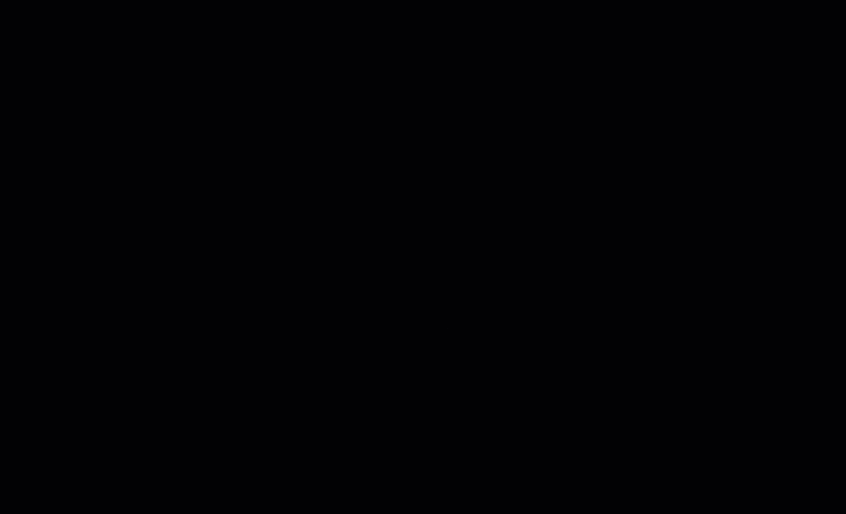
 and select the options in
and select the options in  and select the option in
and select the option in  and select the option in
and select the option in 


